Математическая модель эксперта при оценке информационной безопасности системы

ВЕСТНИК 2016

Сохранность конфиденциальной информации является основной задачей службы безопасности компании. Однако прежде чем осу- ществлять какие-либо мероприятия по защите конфиденциальных данных, необходимо оценить стоимость этой информации, уровень ее защищенности и ее важность (значимость) для организации. Для оценки этих параметров обычно привлекаются эксперты. В работах [1–6] нами рассматривалась методика оценки рисков утери конфиденциальной информации в компании, была построена математическая модель процессов хранения, передачи и потери конфиденциальной информации, а также был разработан программно-аналитический комплекс для экспертных оценок стоимости конфиденциальной информации. Целью данной статьи является разработка вероятностной модели эксперта и оценка ее статистических характеристик.

В данной работе предполагается, что эксперт на основании своих знаний и опыта выбирает ту или иную оценку по n -балльной шкале (от 0 до n ) [3]. Однако поскольку число n достаточно велико, для эксперта равновероятным является выбор не одной, а нескольких оценок. Например, высоко оценивая некоторый показатель по 10-балльной шкале (далее в расчетах всюду n = 10), эксперт может равновероятно указать как 10, так и 9 (или даже 8). Для учета этого обстоятельства нами предлагается использовать распределение вида:

Р ( к ) =------ A ----- , к = 0,..., n (1)

1 + ( а ( к - m )) ^в

ВЕСТНИК 2016

где а , в , m — параметры, а

A = f у_____1_____)               (2)

( k = 0 1 + ( а ( к - m )) ^в )

- нормировочный множитель. На рис. 1 приведены графики функции (1) при разных значениях параметра m : m = 5 - левая, более низкая кривая и m = 10 - правая кривая. Параметр в (всегда положительное четное число) отвечает за крутизну склонов экстремума. На рис. 2 приведены три зависимости в = 2 (кривая с минимальной модой и самыми пологими склонами), в = 10 и в = 20 (кривая с самыми крутыми склонами).

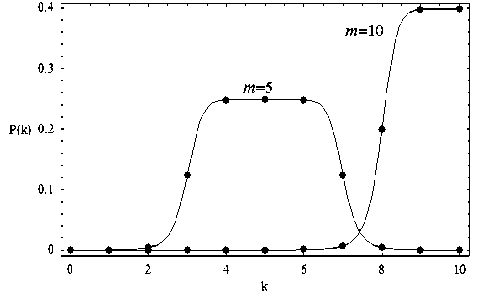
Рис. 1. Зависимости Р ( к ); а = 0,5; в = 10

Однако число равновероятных оценок регулирует в выражении (1) не параметр в, а параметр а. На рис. 3 сопоставлены кривые при различных значениях этого параметра. Самая высокая кривая соответствует а = 0,8 (одна мак- симальная оценка), средняя - а = 0,5 (3 равновероятные оценки) и, наконец, самая низкая -а = 0,3 (5 равновероятных оценок).

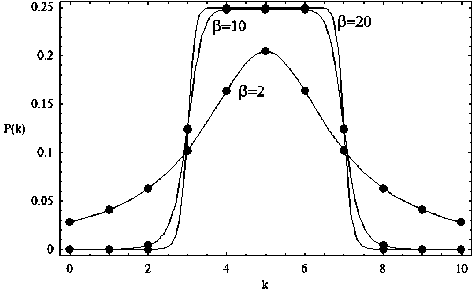
Рис. 2. Зависимости Р ( к ); а = 0,5; m = 5

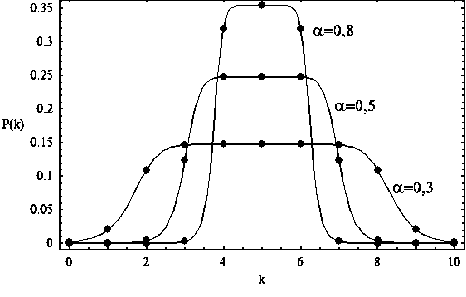
Рис. 3. Зависимости Р(к) ; в = 10; p = 5

Поскольку к = m соответствует моде распределения, есте ственно считать m справедливой оценкой, причем соответствующей методу максимального правдоподобия (то есть, как минимум состоятельной и эффективной). Однако, как видно из рис. 1, 2, 3, для эксперта фактически равновероятными являются и другие оценки. На рис. 4 показана зависимость от параметра m математического ожидания для распределения (1), (2). Математическое ожидание вычислялось в дискретных точках. На рисунке они соединены. Тонкой линией показана биссектриса. Видно, что внутри диапазона математическое ожидание и параметр m хорошо совпадают. Отличие возникает на концах диапазона примерно на балл. Например, если оценивается качество выполнения какой-либо работы, то для хороших работ оценка может быть занижена, а для плохих - завышена.

Нетрудно рассчитать и производящую функцию распределения (1):

nk

^( z) = У —A0----.(3)

k=01 + (а(k - m))в’

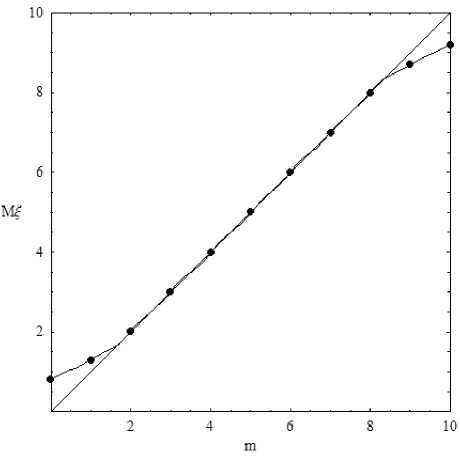
Рис. 4. Зависимость математического ожидания от параметра m ; α = 0,5; β = 10

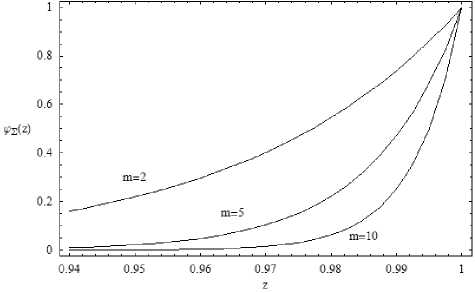
Рис. 6. Зависимости φ_∑ ( z ); α = 0,5; β = 10

На рис. 5 показаны зависимости производящей функции от z при разных значениях m . Предположим, что для оценки определенного показателя привлечено N экспертов. Предполагая, что результаты экспертиз попарно независимы, можно найти итоговую производящую функцию по формуле:

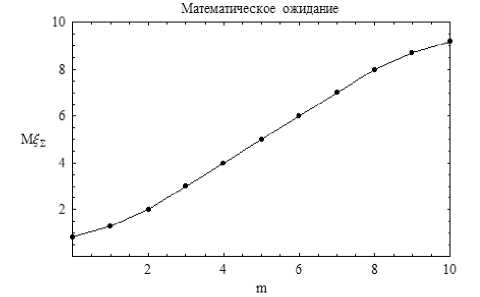
Рис. 7. Среднее математическое ожидание α = 0,5; β = 10, N = 15

Ф т ( z )

n

= z

< k = 0

A о z^k

1 + ( a ( k - m )) ^e _y

\ N

,

графики которой при N = 15 представлены на

Точно такую же кривую можно получить, если рассчитать итоговую производящую функцию по формуле:

ВЕСТНИК 2016

рис. 6.

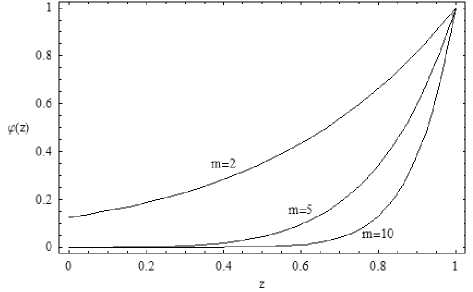
Рис. 5. Зависимости φ(z) ; α = 0,5; β = 10

^ ( z) =

' ^  A (z / N)k  ^ N vk=01 + (a(k - m))e J

,

вычислить производную и положить в z = 1.

Сравнивая рис. 4 и 7, видим, что, как и сле-

Если найти производную уравнения (4) и положить z = 1, можно найти математическое ожидание суммарного балла, полученного от всех экспертов, а поделив это число на N , можно найти среднее математическое ожидание (см. рис. 7):

M^ = ^ (1)/ N .                         (5)

довало ожидать, увеличение числа экспертов не исправляет кривую и не приближает ее к биссектрисе, поскольку кривые идентичны, что можно показать и аналитически. Поэтому по рис. 4, зная оценку математического ожидания, можно легко находить оценку параметра m , что и является целью исследования, причем независимо от N .

Для того чтобы подчеркнуть особенности данного распределения, рассмотрим графики вероятностей при различных значениях m (рис. 8).

Во-первых, видим, что на концах интервала при m = 0 и при m = 10 моды принимают значения ≈1 и ≈9 соответственно, что согласуется

с нашими выводами и рис. 7. Во-вторых, что на середине интервала между 2 и 8 величина моды

не зависит от m и практически одинакова.

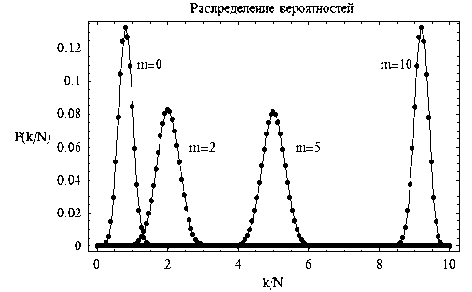
Рис. 8. Графики вероятностей P ( k / N ) , α = 0,5; β = 10, N = 15

В заключение для полноты картины рассмот-

ВЕСТНИК 2016

рим зависимость дисперсии и среднего квадратичного отклонения от параметра m (рис. 9 и 10 соответственно).

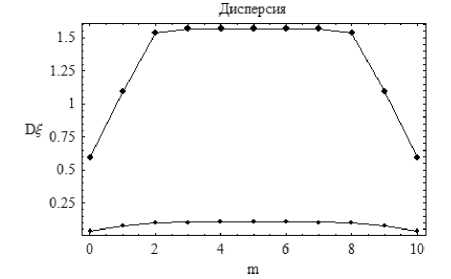
Рис. 9.

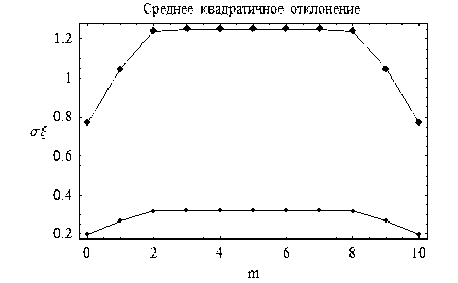
Рис. 10

Дисперсия (рис. 9) и среднее квадратичное отклонение (рис.10), α = 0,5; β = 10, N = 1 и 15.

На рис. 9 и 10 верхние кривые соответствуют N = 1 (дисперсии исходного распределения), нижние кривые N = 15. Как видно из рис. 10, значения среднеквадратичных отклонений вполне приемлемы.

Для вычислений дисперсий использовались хорошо известные формулы:

D^ = ^'(1) + ^"(1) - (^'(1))2 при N = 1 и D^ = ф'(1) + ф'(1 - (ф'(1))2 при N = 15, причем σξ= Dξ , а σξΣ= DξΣ.

При больших значениях N ( N = 15 вполне достаточно) справедлива центральная предельная теорема и, как видно из рис. 8, итоговое распределение переходит в нормальное f_N ( k ). Как видно из рис. 11, отклонение итогового распределения от гауссового незначительно.

Отличие итогового распределения от нормального

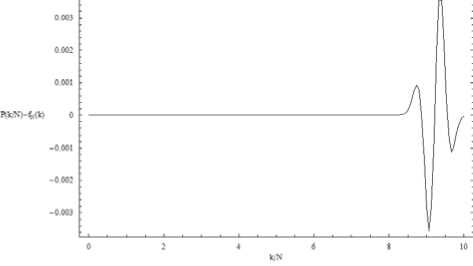
Рис. 11. График отличия вероятностей P ( k / N ) – f_N ( k ), α = 0,5; β = 10, N = 15

Таким образом, в настоящей работе, являющейся продолжением работ [1; 2; 4; 5] предложена математическая модель эксперта, проводящего оценку по достаточно длинной n -балльной шкале. При этом учитывается возможность случайного выбора из равновероятных оценок. Обоснована введенная для этой цели в работе функция распределения. Проанализированы параметры функции распределения, отвечающие за число равновероятных оценок и крутизну склонов. Исследованы характеристическая функция, математическое ожидание и дисперсия. Рассмотрен случай привлечения к оценке N экспертов. Исследована связь математического ожидания и оцениваемого параметра и указан метод определения (корректировки) оцениваемого параметра по математическому ожиданию.