Математическая модель эволюционно стабильной стратегии для популяции в условиях конкуренции на неоднородном ареале

Конкуренция, наряду с хищничеством, – один из наиболее распространненых типов взаимодействия между живыми организмами на всех уровнях, от вирусов [1] и бактерий [2; 3] до растений и животных [4; 5]. Недавние исследования [5; 6] показали, что это явление присуще даже клеткам в эпителиальных и других тканях высших организмов[7; 8]. Клеточная конкуренция участвует в различных физиологических и патологических процессах и является важнейшим гомеостатическим механизмом, необходимым для эмбрионального развития, профилактики заболеваний и старения [9–11].

Основная причина конкуренции – это соперничество за ресурсы (вода, свет, пища, территория и т. д.), количество которых, как правило, ограничено. Конкурентные отношения составляют неотъемлемую часть борьбы за существование в экологическом сообществе, определяемом как совокупность популяций по крайней мере двух различных видов, взаимодействующих в пределах определенной (географической) области [12; 13].

0000-0001-6598-8521

Эта статья доступна в соответствии с условиями лицензии Creative Commons Attribution-NonCommercial 4.0 International

License (CC BY-NC 4.0)

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License (CC BY-NC 4.0)

Внутривидовая и межвидовая конкуренция оказывает сильное влияние на динамику конкретной популяции, видовое разнообразие [14] и структуру всего экологического сообщества [15]. Существуют различные механизмы и формы конкурентных отношений [5]. На самом общем уровне можно выделить прямую конкуренцию, при которой две популяции одного или разных видов вступают в открытую конфронтацию, реализующуюся во всяческих способах взаимного угнетения (схватки, аллелопатия и пр.), и косвенную конкуренцию, когда одна из популяций опосредованно влияет на другую, ухудшая условия ее существования (опережение, монополизация пространства и пр.). В любом случае конкуренция всегда снижает общую приспособленность обоих участников этого процесса [16].

Согласно принципу конкурентного исключения (закон Гаузе) [17], менее приспособленный вид в долгосрочной перспективе обречен либо на вымирание, либо на вытеснение в другую экологическую нишу [18]. Этот принцип предсказывается теоретическими рассуждениями, математическими моделями и лабораторными экспериментами, однако почти не наблюдается в естественных экосистемах [19]. Считается, что одним из основных механизмов, сохраняющим сосуществование популяций и объясняющим разнообразие видов в биологических сообществах, является компромис между конкуренцией и колонизацией [20]. Так, виды, которые больше преуспели в конкурентной борьбе, будут доминировать на конкретном участке ареала или в определенной экологической нише, приобретая более «специализированную» стратегию, в то время как виды, обладающие «универсальной» стратегией, будут активнее колоннизировать другие участки ареала или занимать новые экологические ниши [21].

Важным вопросом является то, какую стратегию выберет каждая из взаимодействующих популяций, и приведет ли она ее к успеху, т.е. будет ли эта стратегия устойчивой в эволюционном смысле [22]. Эволюционно стабильной стратегией (ЭСС) называется такая стратегия поведения, направленная на решение адаптационных задач, при которой популяция обеспечивает свое долговременное существование и не может быть вытеснена с ареала аналогичной популяцией с другой стратегией [23]. ЭСС относится к области теории игр: существует предположение, что индивидуальная приспособленность особей популяции может рассматриваться как аналог теоретико-игрового понятия полезности или выгоды, представляющей собой величину, измеряющую то, что игроки оптимизируют для достижения своих целей [24].

В неоднородной среде обитания интересным представляется также возникновение и эволюция пространственного распределения видов [25–27]. Одним из основных математических инструментов для анализа пространственно-временных процессов в биологических сообществах являются уравнения в частных производных, позволяющие описать процессы формирования устойчивых пространственных структур [28; 29]. В качестве одной из теоретических моделей реализации пространственного распределения популяции на неоднородном ареале, приводящей к ЭСС, является идеальное свободное распределение (ИСР) [30]. Согласно теоретической модели ИСР, все особи популяции размещаются пропорционально доступному на ареале ресурсу, имеют идеальное представление о его распределении и возможном изменении со временем и могут свободно перемещаться по ареалу с целью повысить свою индивидуальную приспособленность [31]. ИСР, изначально введенное для одного вида, рассматривалось для систем «хищник – жертва» [32–34] и нескольких видов, конкурирующих за общий ресурс [35]. В работах [36; 37] для системы «хищник – жертва» ИСР рассматривается как пропорциональность распределения обоих видов в стационарном или осциллирующем режиме. В статье [38] описан более общий случай ИСР-подобного распределения, когда обобщенному ресурсу пропорциональна только «жертва», а в распределении «хищника» возможны различные варианты.

В исследовании рассматривается математическая модель стратегии для одной из двух конкурирующих за общий ресурс родственных популяций на неоднородном ареале. Построение модели ведется на основе принципов ИСР с целью получения ЭСС для выбранной популяции.

Материалы и методы

Модель двух конкурирующих популяций

Рассмотрим для описания динамики численности двух конкурирующих за единый ресурс популяций V , V систему дифференциальных уравнений в частных производных (одномерная модель диффузии – реакции) [39; 40]

‘V- = D 1 — VV + a l V 1 p ( ^x )^{- b} 11 V 1 ^{2 -} d t       О x

b i VV ,

S

V = D 2 ^ VT + a 2 V 2 P ( x ) - ^b 22 V -d t       dx

b 2 V 1 V 2 ,

где D, D₂ — коэффициенты диффузии, a_{, a₂ — коэффициенты роста обеих популяций соответственно, а p ( x ) -неравномерно распределенный на ареале ресурс. Отметим, что функция ресурса нигде на ареале не обращается в нуль и имеет достаточное количество производных, что облегчает общий анализ системы. Коэффициенты b 1, ^b22 отвечают за конкуренцию между особями внутри каждой популяции, а b ₂, b₂₁ - за конкуренцию между популяциями. Переменная x изменяется на отрезке [ 0;1 ] , на концах которого задаются какие-либо граничные условия. Так же, система (1) дополняется начальными условиями распределения популяций на ареале.

Обилие коэффициентов затрудняет анализ модели.

Заменой

t = i, k , = Dl, k 2 = D a ₁          a ₁           a ₁

,

a ₁

a ₂

S Г, = -U U1,V2 = -U U 2, b11           b22

Y = a ² , e , = b ² , ₽ 2 = b²²

a 1         b 22         b 11

система (1) может быть сведена к виду

U = к

5 г     ¹

S

U = k ar      •

d²U , 5 x ²

d ² U ₂

² 5 x ²

+ ^U 1 [ Р ( ^x ) - ^U 1 - ^e i Y ^U 2 ] ,

, (3)

+ Y U2 Р ( x )- — U1

_          Y

- U ₂

.

Будем считать, что рассматриваемые популяции относятся к одному виду или к малоотличающимся родственным видам [41], так что их коэффициенты роста одинаковы ( a = a₂ , Y = 1), а коэффициенты диффузии достаточно малы ( k , k₂<  1) и подчиняются условию

k₂ = е к , , ( 0 <  £ <  1 ) .                    ( 4 )

Обозначая производную по времени точкой, а по координате штрихом и учитывая вышесказанное, получим

u 1 = kU 1' + u 1 [ p ( X ) - u 1 - в и 2 ] ,

U 2 = £ kU 2 + U 2 [ Р ( X ) - в 2 U 1 - U 2 ] ,

где PP P2 - коэффициенты межпопуляционной конкуренции в нормированных переменных.

Дополним систему (5) условиями периодичности

U 1 ( 0,т ) = U 1 ( 1,т ) , U 2 ( 0,т ) = U 2 ( 1,т )      ( 6 )

и начальными условиями

Ц ( x , 0 ) = U 0 , U 2 ( x , 0 ) = U ₂ ⁰ .           ( 7 )

Постановка задачи

Цель настоящего исследования состоит в попытке построить эволюционно стабильную стратегию для популяции, находящейся в условиях конкуренции со стороны родственной популяции на неоднородном ареале. Суть такой стратегии заключается в том, чтобы выработать некоторое правило поведения (одно или несколько), обеспечивающее долговременное существование указанной популяции при воздействии неблагоприятных факторов, например, увеличения негативного влияния со стороны конкурента, скачки численности, вызванные

внешним влиянием, и т. д. Математически это должно выражаться в четком понимании того, какие параметры модели должны быть изменены, для того, чтобы выполнялись упомянутые выше правила, формирующие стратегию.

Исходя из начально-краевой задачи (5)-(7), выберем в качестве фокус-популяции, т. е. популяции носителя выстраиваемой эволюционно-стабильной стратегии популяцию U . Согласно приведенной математической модели, наша фокус-популяция обладает всего тремя возможными механизмами управления своей стратегией, заключающимися в изменении: 1) параметра диффузии е; 2) коэффициента конкурентного взаимодействия Р₂ ; 3) начальных условий U ⁰ . Отметим, что величина популяции и ее распределение в начальный момент времени важны в основном при рассмотрении стартовой задачи, возникающей в случае инвазии или заселении вида на новую территорию (место обитания). Разнообразные сценарии развития пространственно-временной динамики системы (5)–(7), возникающие при вариации парметров указанных пунктов, будут рассмотрены ниже.

Методы решения

Для поиска и исследования устойчивости стационарных решений модели (5)–(7) в работе используются стандартные методы математического анализа, теории динамических систем на фазовой плоскости [42; 43] и асимптотического анализа дифференциальных уравнений с малым параметром при производной [44].

Для численного решения сформулированной начально-краевой задачи, основу которой составляет система дифференциальных уравнений в частных производных типа «диффузия - реакция», применяется модифицированный интегро-интерполяционный метод (метод баланса) с дискретизацией на основе смещенных сеток и метод прямых с интегрированием по схеме Рунге - Кутты четвертого порядка, детально описанный в работах [45; 46]. Для реализации метода в среде MATLA B разработан комплекс программ SPECIES -21, защищенный свидетельством о государственной регистрации программ для ЭВМ [47]. Данный комплекс позволяет проводить вычислительные эксперименты для нелинейных диффузионно-адвективных моделей, описывающих пространственно-временную динамику взаимодействующих популяций в условиях неоднородности среды обитания.

Результаты и обсуждение

Начнем анализ модели (5)–(7) в предположении, что коэффициент диффузии настолько мал, что им можно пренебречь ( k = 0). Тогда уравнения (5) могут быть записаны в виде

и 1 = U 1 [ p ( x ) - U 1 - e i U 2 ] ,

U 2 = U 2 [ P ( x ) - в 2 и 1 - U 2 ] .

Система (8) имеет тривиальное стационарное решение { U , U₂ } = { 0,0 } и три стационарных решения, отвечающих ИСР

{ P ⁽ x ^),0 }

{ °, P ⁽ x ) }

I 1(1 -ил

p ( x ),

1 -0 1

1 — 0 1 0 2

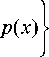
(9, а )

(9, б )

(9, в )

Выполнение условия (10, в ) приводит к стабильному сосуществованию обеих популяций на ареале с пространственным распределением, пропорционам ресурсу p ( x ) , причем та популяция, чей коэффициент конкурентного взаимодействия (Р_;, z = 1,2 . ) меньше, будет доминировать по своей численности. Если, например, 02 < 01 <  1, то независимо от начальных условий, в системе (8) установится стационарное состояние (9, в ), при котором фокус-популяция будет располагаться выше конкурента, как показано на (рис. 1), где начальные условия U 0 ( x ) = 0,6, U 0 ( x ) = 0,3, а функция ресурса задается выражением:

Анализ стационарных решений (9) показывает, что их устойчивость определяется условиями:

P(x)

=  + Sin nx .

в1 < 1, | в1 >1 , в1 < 1 , в2 > 1 , в2 < 1, в2 < 1 .

( 10, а )

( 10, б )

( 10, в )

Условие (10, а ) означает, что вторая популяция U₂ уступает в конкурентной борьбе первой U и в конечном счёте полностью вытесняется ею с ареала. Поскольку U₂ — это наша фокус-популяция, то такой вариант развития событий с точки зрения выстраивания эволюционно стабильной стратегии совершенно неприемлем.

Условие (10, б ) - полная противоположность условию (10, а ) и соответствует эволюционным задачам фо-кус-популяции - по возможности победить в конкурентной борьбе и сохранить свое существование в течение длительного временного промежутка.

Отметим, что даже в случае Р[ <  Р₂ <  1 стратегию фокус-популяции можно также считать эволюционно устойчивой, так как она позволяет сохранять U ₂ ( x ) >  0 на ареале бесконечно долго, пусть даже и уступая U j ( x ) по численности. При Р[ = Р₂ = 1 возникает очень интересная ситуация, приводящая к появлению целого семейства стационарных решений, описываемого теорией косиметрии [48; 49]. Однако в реальности такое совпадение маловероятно и здесь рассматриваться не будет. Условие же 0i,0₂ >  1 описано ниже.

Исследуем теперь поведение системы (5)–(7) при наличии диффузии и рассмотрим вопрос о ее влиянии на стационарные состояния (9). Будем искать решение возмущенной (малым параметром k ) системы (5) в виде:

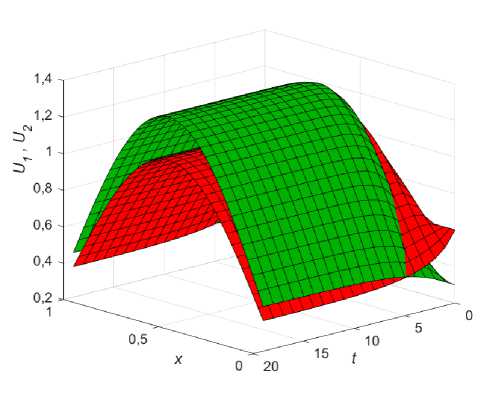
Рис. 1. Распределение фокус-популяции (зеленый) и популяции конкурента (красный) на ареале с неоднородным распределением ресурса p ( x ) для стационарного состояния (9, в ) при р 1 = 0,3; р ₂ = 0,15

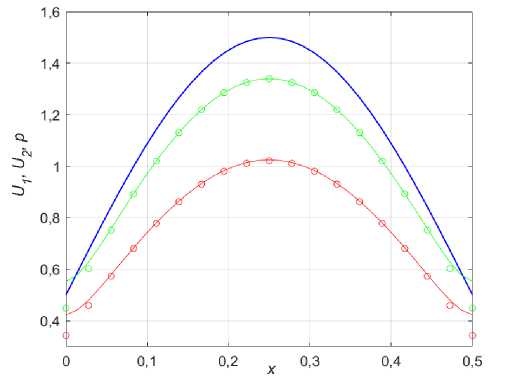
Рис. 2. Сравнение распределений U (красный) и U₂ (зеленый) по отношению к ресурсу p (синий) рассчитанных численно (линии) и асимптотически (шарики) при k 1 = 0,001; £ = 1, Р 1 = 0,35; р ₂ = 0,15

и 1 = U 10 + k i U 11 + kyU 12 +••• , <

_ U 2 = U 20 + k 1 U ₂₁ + k\U 22 +• .

Подставляя (12) в (5) и ограничиваясь первыми двумя членами асимптотического разложения, получим приближенное решение:

U 1   1 — в 1 в 2 (	.      p "( x ) p ( x )+ k 1 p ( x ) l	1 -. 1 -P 1	£в 1 1 — в 2 .	, 1 ( 13 )
U 2 =	/ \     P ”( x ) - p ( x ) + k j    1	£	β 2 -	.
2   1 - в 1 в 2	1 p ( x )	. 1 - в 2	1 — в 1.	]

На рис. 2 изображены распределения популяций в сравнении с ресурсом при наличии малой ( к 1 = 0,001) диффузии. Сплошными линиями показано решение, полученное с помощью численного метода, а шариками -по формулам (13). Видно, что диффузия «растаскивает» исходное, пропорциональное p ( x ) решение (9 в ) по краям, уменьшая его максимум в центре ареала. По мере увеличения диффузии этот эффект становится все сильнее, правда результаты, полученные с помощью выражений (13) становятся менее достоверными, так как к перестает быть малым параметром. Наличие диффузии в системе (5)-(7) нарушает ИСР, но все же при к1<^1 стационарные решения такого рода могут быть названы ИСР-подобными [36-38].

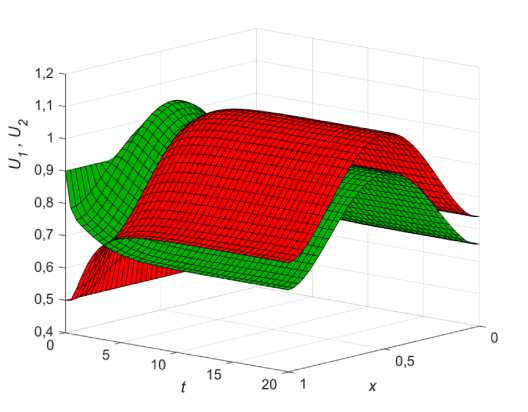
Общий анализ уравнений (13) показывает, что изменение параметра диффузии £ может быть использовано фокус-популяцией для улучшения своей приспособленности на ареале, так, например, при в1 < в2 < 1 устанавливается равновесие, при котором численность первой популяции больше, чем численность второй, однако если последняя уменьшит свою диффузию путем изменения ε , то с течением времени сможет добиться локального перевеса в месте максимума ресурса, сохраняя при этом общее равновесие системы (рис. 3).

Заметим, что, несмотря на разницу стартовых условий ( U 0 >  U 0 ), снижение коэффициента конкурентного взаимодействия в₂ <  в 1 и сильные изменения в коэффициенте диффузии ( £ = 0,1... 0,01), фокус-популяция не сможет полность вытеснить конкурента с ареала до тех пор, пока будет выполнено условие (10 в ). Это связано с тем, что собственные значения линеаризованной системы (5)-(7) лежат строго в левой комплексной полуплоскости и не могут перейти в правую при условии в₁₂ <  1 [50]. Потеря устойчивости положения равновесия (9 в) может произойти лишь при нарушении условия (10 в ).

Рассмотрим поведение системы (5)–(7) в случае, когда в 12 >  1. Как уже было сказано выше, стационарное состояние, при котором на ареале сосуществуют оба вида, станет неустойчивым, и малейшее возмущение приведет со временем к гибели одного из видов. Можно сказать, что конкурентная борьба сильно обостряется, теперь уже не может быть мирного сожительства с разными численностями U_x ( x ) и U ₂ ( x ) , выживает та популяция, которая сможет эффективнее снизить конкурентное влияние другой. В этом смысле для того, чтобы фокус-популяции сохранить свою стратегию эволюционно стабильной, необходимо просто побеждать в кон-куретной борьбе (1 <  в₂ <  в 1 ). Однако возможны и другие варианты.

а

Рис. 3. Влияние коэффициента диффузии фокус-популяции на решение (9, в ) при в 1 = 0,3; в ₂ = 0,38; к 1 = 0,03;

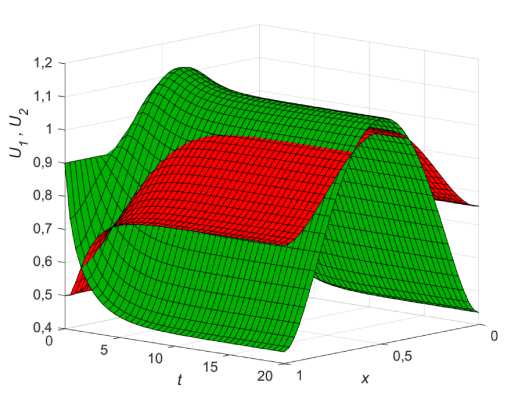
б

U 1 ⁰ = 0,5; U 0 = 0,9 : а - диффузия одинакова (£ = 1); б - диффузия фокус-популяции меньше ( £ = 0,1)

Предположим, что фокус-популяция проигрывает в конкурентной борьбе (1 <  в1 <  вг ), но У нее остается возможность варьировать начальные условия и коэффициент диффузии. Покажем на конкретных вычислительных примерах, что оба этих параметра могут привести к смене стационарного решения.

Пусть изначально коэффициенты диффузии равны, е = 1, и Р[ = 1,15 <  Р₂ = 1,2 , тогда если начальное распределение U 0 >  U 0 , то первая популяция однозначно выигрывает конкурентную борьбу у второй (рис. 4, а ).

Данное стационарное решение сохраняется даже при небольшом начальном перевесе фокус-популяции (рис. 4, б ), но начиная с некоторой разницы в численности, может установиться стационарное состояние, соответствующее сосуществованию видов (рис. 4, в ), которое будет неустойчивым по отношению к возмущению других параметров. Наконец, при дальнейшем увеличении разницы в начальных распределениях фокус-популяция быстро вытесняет конкурента со всего ареала (рис. 4, г ).

Вопрос о нахождении точного соотношения между начальными распределениями популяций задающего условие смены стационарных решений интересен, но выходит далеко за рамки данной работы.

Известно [42; 50], что разность в коэффициентах диффузии может также привести к смене равновесия (рис. 5). В таких случаях говорят о так называемой неустойчивости Тьюринга [51].

Естественно, что получить перевес в конкурентной борьбе при 1 < в1 < вг фокус-популяция может, комби- нируя изменения упомянутых выше двух параметров (U0,е ). Особенно интересен этот вопрос в случае инвазии одного из видов или освоения (заселения) новых территорий, когда начальные распределения по ареалу не постоянны (U02 = f (x)).

Рассмотрим вначале случай, когда p (x) = 1 + “ sin f 2nx

π

—

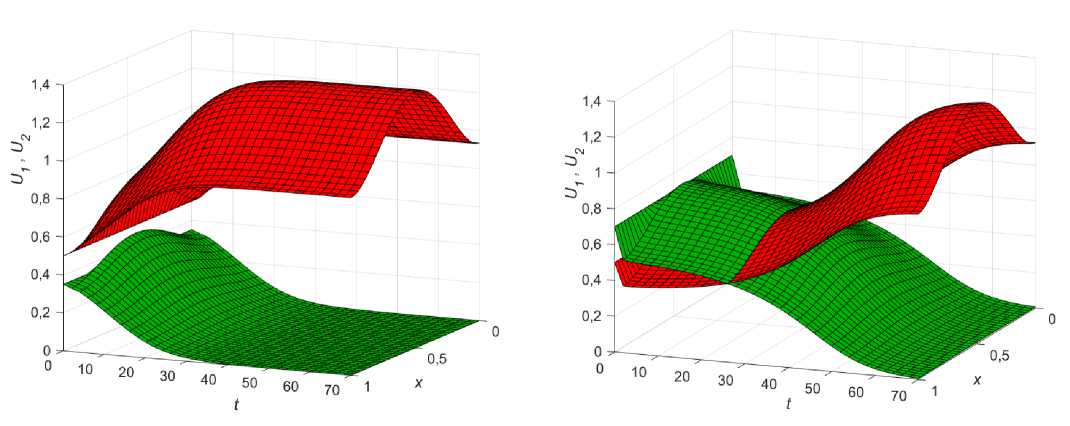
а                                                     б

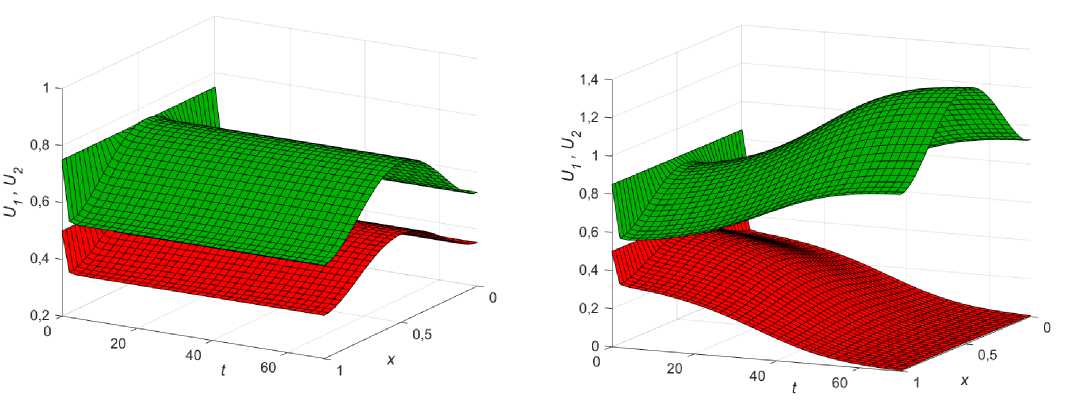
в                                                                   г

Рис. 4. Влияние начальных условий на решение системы (5)-(7) при в1 = 1,1; вг = 1,15 ^: а - U 0 = 0,5; U 0 = 0,35; б - U 0 = 0,5; U 0 = 0,7 ; в - U 0 = 0,5; U 0 = 0,75 ; г - U 0 = 0,5; U 0 = 0,85

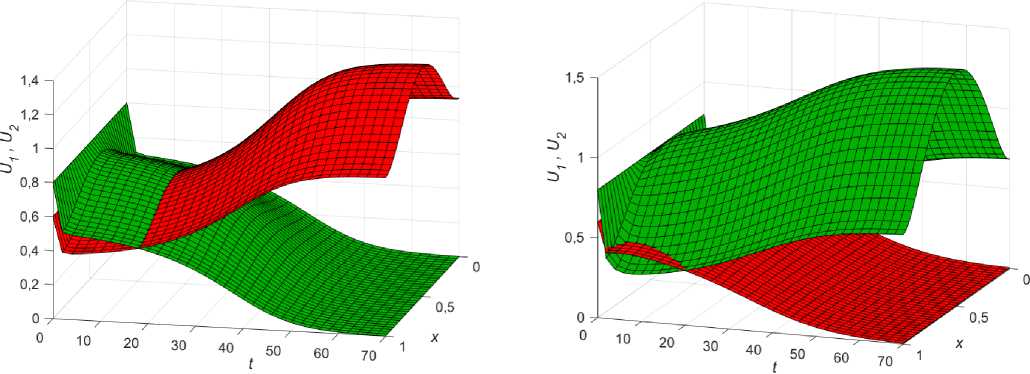
а

б

Рис. 5. Смена стационарного решения (вх = 1,1; вг = 1,15; к = 0,03; U 0 = 0,6; U 0

= 0,8 :) а - е = 1; б - е = 0,1

в                                                               г

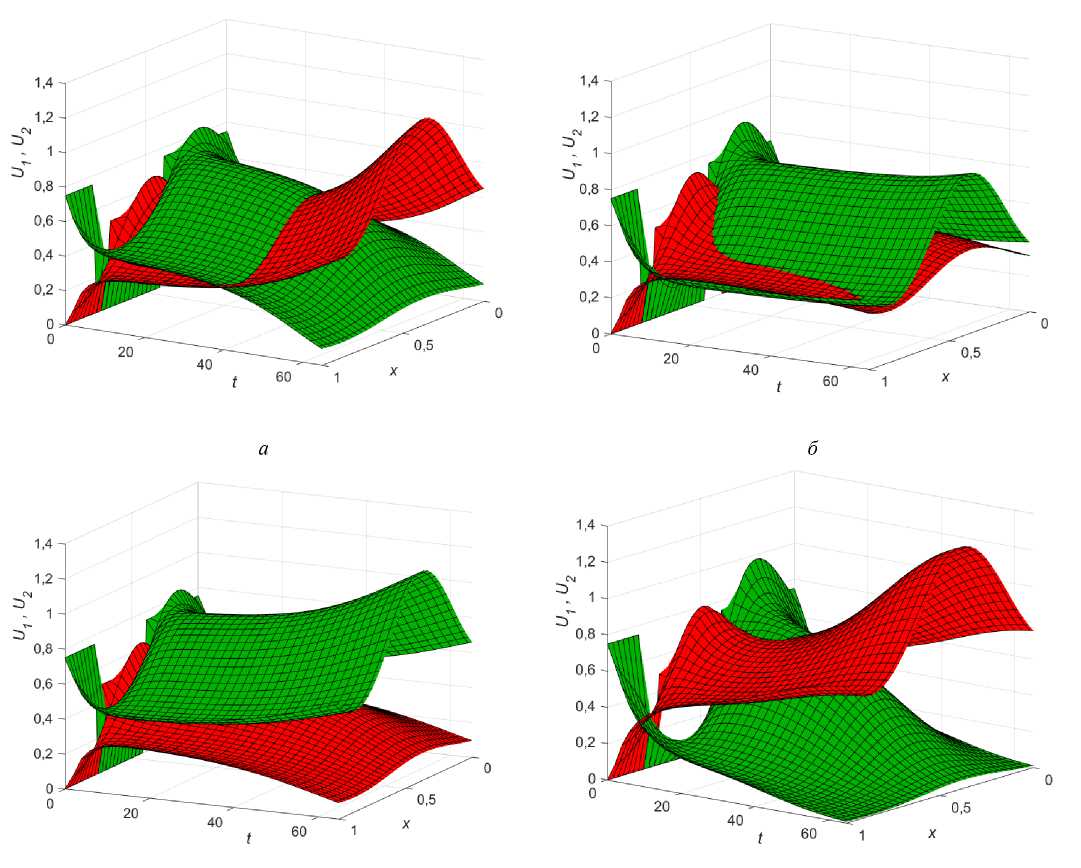
Рис. 6. Смена стационарного решения (Р[ = 1,1; Р₂ = 1,15; к = 0,01, U 0 , U 0 определены из (15)-(16):

а - е = 1; б - е = 0,72 ; в - е = 1, но U ⁰ = 0,75 при x е

9;9

; г - е = 0,2

а начальные численности популяций заданы на постоянном уровне, но на всем интервале:

0,5

U0 (x ) = 1

0,

( 1  7

при x el -;-

_ ( 1 7

при x gl —

0,

при x e

U0 (x Н

0,75

при x g

9;6

9;6

Как показано на рис. 6, а , несмотря на интегральное превосходство в начальный момент времени, фокус-популяция тем не менее проигрывает в долгосрочной перспективе при равных коэффициентах диффузии и 1 <  в1 <  вг ■ С уменьшением коэффициента диффузии

(е <  1) ситуация начинает меняться, и при определенном пороговом значении (е <  0,73) фокус-популяция переигрывает конкурента (рис. 6, б ). Этого же результата можно добиться и увеличением начальной численности U 0 ( x ) , например сужая отрезок с нулевым количеством фокус-популяции с [ 4/9;5/6 ] до [ 4/9;7/9 ] , как это видно на (рис. 6, в ). Отметим, что увеличение U 0 ( x ) повышает пороговое значение s и позволяет второй популяции добиваться превосходства при меньшем изменении коэффициента диффузии. Однако чрезмерное снижение коэффициента диффузии может привести к обратному эффекту, например, если е = 0,2 , то превосходства на ареале добивается первая популяция (рис. 6, г ). Это связано с законом распределения ресурса на ареале, сильная диффузия приводит к тому, что фокус-популяция «проскакивает» максимум и не может до достичь критического перевеса в локальных точках до-

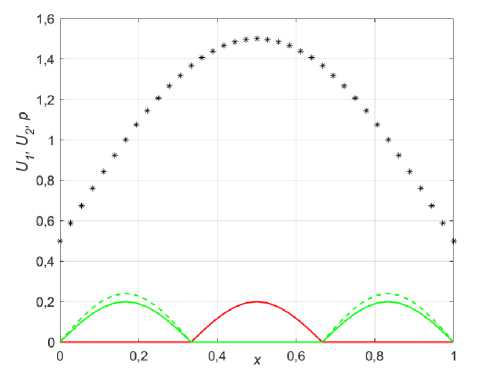
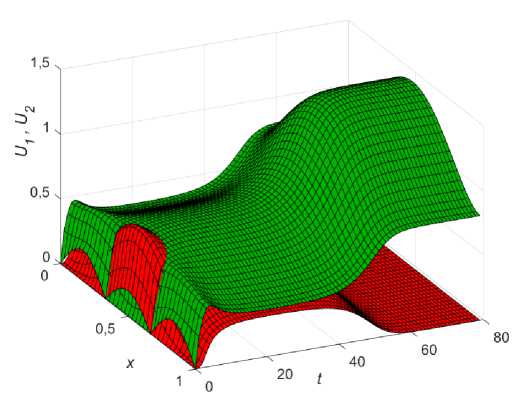
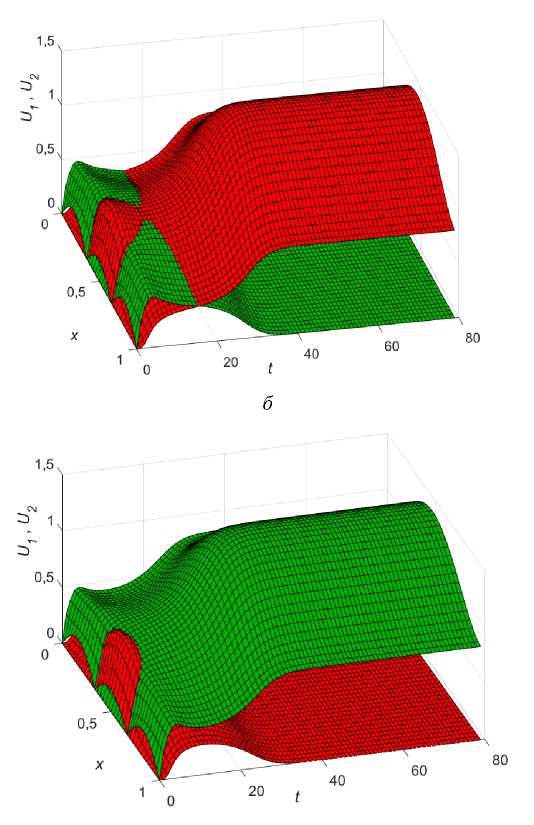
Рис. 7. Начальное распределение и сценарии конкурентного взаимодействия популяций при колонизации р! = 1,35; р₂ = 1,4; к = 0,01; p ( x ) = 1/2 + sinn x : а - сравнение распределения ресурса (звездочки) с U 0 (красный), исходным U ⁰ (сплошной зеленый) и увеличенным U ⁰ (зеленый пунктир); б - сценарий взаимодействия при е = 1; в - параметр е = 1, но U ⁰ возросло; г - диффузия фокус-популяции сильно меньше (е = 1,2)

г

стичь критического перевеса в локальных точках пространства, в результате чего и проигрывает в долгосрочной перспективе в целом.

Рассмотрим теперь случай колонизации (заселения новых территорий), когда оба вида прибывают (высаживаются естественным путем) в неосвоенную область ареала или новую среду обитания. Пусть функция ресурса в этой области задана выражением (11). Предположим также, что первая популяция имеет прямое конкурентное преимущество (1 <  в1 <  Р₂ ) и согласно концепции ИСР высаживается на новом ареале в том месте, где расположен максимум ресурса. Несмотря на интегральное численное превосходство фокус-популяции (площадь под зеленой кривой в два раза больше чем под красной, (рис. 7, а )), при равной диффузии она проигрывает конкуренту (рис. 7, б). Однако уже небольшое увеличение начальной численности ( U 0₂ - U ⁰j ® 10 %) приводит к тому, что с течением времени вторая популяция вытесняет первую (рис. 7, в ). Ускорения этого процесса фокус-популяция может добиться, успользуя увеличение своей диффузии. Действительно, поскольку особи второй популяции распологаются по обе стороны от максимума ресурса, то рост диффузии приведет к ускоренному их проникновению в центр ареала, создавая критическое количество, необходимое для победы в конкурентной борьбе (рис. 7, г ).

Интересна также ситуация, когда при колонизации оба вида не имеют представления о функции ресурса в новой среде обитания и распределяются равномерно в шахматном порядке (рис. 8, сплошные кривые).

Пусть, как и прежде, 1 <  в1 <  Р₂ и функция ресурса имеет вид (11). Будем для сравнения наблюдать за плотностями популяций в двух точках ареала с координатами x = 0,25 (сплошные линии на рис. 9) и x = 0,45 (пунктирные линии на рис. 9). При равных численностях популяций победу в конкурентной борьбе одержит U , как

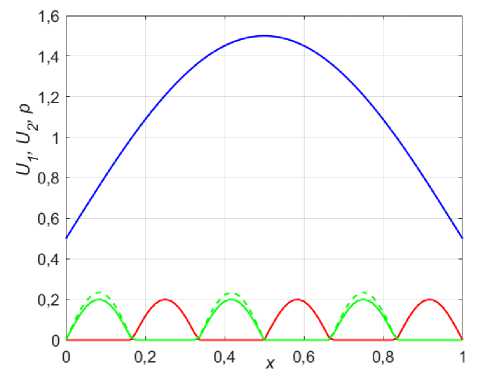
Рис. 8. Начальное распределение U_x (красный)

и U₂ (зеленый) по отношению к ресурсу p (синий) при U ⁰ = U ⁰ (сплошные) и U ⁰ >  U ⁰ (пунктир)

это видно на (рис. 9, а). В этом случае ни увеличение, ни уменьшение диффузии (даже очень маленькое) не может помочь фокус-популяции переиграть конкурента. Например, уменьшение k ₂ (от е = 1 до е = 0,1) приводит к динамике, изображенной на (рис. 9, б) . Добиться превосходства U можно, лишь увеличив начальное распределение U ⁰ >  U ⁰ (зеленый пунктир на рис. 8). Динамика такого сценария изображена на (рис. 9, в ). При численном перевесе на старте фокус-популяция может позволить себе изменение коэффециента диффузии и в меньшую и в большую сторону, однако до определенного предела. Например, при увеличении k уже при е = 1,1 (рис. 9, г ) верх одерживает популяция U_x . При уменьшении k ситуация чуть лучше, однако по достижении е = 0,15 U опять выигрывает.

Таким образом, при колонизации в условиях неопределенности и равномерном стартовом распределении популяций (при 1 <  в1 <  Р₂ ) может сложиться ситуация (нельзя исключать иные распределения ресурса), когда ЭСС для фокус-популяции состоит только в численном превосходстве начального распределения.

Заключение

Предложенная в статье модель ЭСС для популяции, находящейся в условиях конкуренции на неоднородном ареале, базируется на системе дифференциальных уравнений в частных производных, относящихся к классу уравнений диффузии - реакции. Модель построена с учетом принципа ИСР, позволяющего получать максимальную приспособленность особей популяции к месту обитания. Сама стратегия сводится к определенному набору правил поведения, обеспечивающих долговременное существование в условиях конкурентной борьбы с родственной популяцией за неравномерно распределенный ресурс.

Анализ модели (5) показывает, что система может иметь три стационарных решения (9), которые в общей сложности зависят от трех факторов: нормированных коэффициентов межпопуляционной конкуренции Ри Р2, диффузии (к, е) и начальных условий (U[0, U2 ). Долговременное существование фокус-популяции подразумевает несколько вариантов, худший из которых состоит в простом выживании при численном доминировании конкурента, что соответствует одному из вариантов решения (9 в), а лучший - в полной победе над другой популяцией (конкурент погиб или вытеснен за пределы ареала), что соответствует решению (9 б). Приведем ниже основные правила, придерживаясь которых фокус-популяция будет обладать ЭСС.

В отсутствии диффузии (к = 0) при Р12 < 1 фокус-популяция будет всегда закрепляться на ареале при лю- бых начальных условиях (7), а ее распределение по ареалу будет соответствовать ИСР, как, впрочем, и распределение популяции конкурента. Если при этом необходимо, чтобы ее численность была выше численности конкурента, то должно выполняться неравенство в2 < в1 ■

Наличие малой диффузии приводит к отклонению стационарного решения от ИСР и может быть использовано фокус-популяцией для улучшения своей приспособленности на ареале, так, при в1 <  вг <  1, уменьшая параметр S , она может добиться локального перевеса в месте максимума ресурса, сохраняя при этом общее равновесие системы см. (рис. 3, б).

В случае обострения конкурентной борьбы, когда в12 > 1 и сосуществование двух популяций на ареале становится неустойчивым, фокус-популяции для сохранения ЭСС необходимо либо полностью побеждать в конкуретной борьбе (1 < Р2 < в1), либо при 1 < в1 < в2 варьировать свой коэффициент диффузии и начальные условия в зависимости от внешних обстоятельств. Так, при равных стартовых условиях необходимо снижать диффузию, уменьшая параметр S . В остальных случаях фокус-популяции следует добиваться численного превосходства в начальных условиях и такого изменения параметра s (в большую или меньшую сторрону), которое приводит к быстрейшему притоку особей в места с максимальным значением ресурса. Такие сценарии хорошо проиллюстрированы (рис. 6 и 7).

В данной работе построение ЭСС для популяции в условиях конкуренции за общий ресурс на неоднородном ареале велось на основе одномерной модели диффузии - реакции в предположении, что популяция-конкурент является родственной ( a [ = a ₂, y = 1) , а коэффициенты диффузии достаточно малы ( k , k ₂< 1). Изменение любого из этих условий приводит к усложнению задачи и требует дополнительных исследований. Для будущих задач особо интересны случаи конкурентного взаимодействия с нелинейными коэффициентами диффузии [52; 53].

б

в                                                                 г

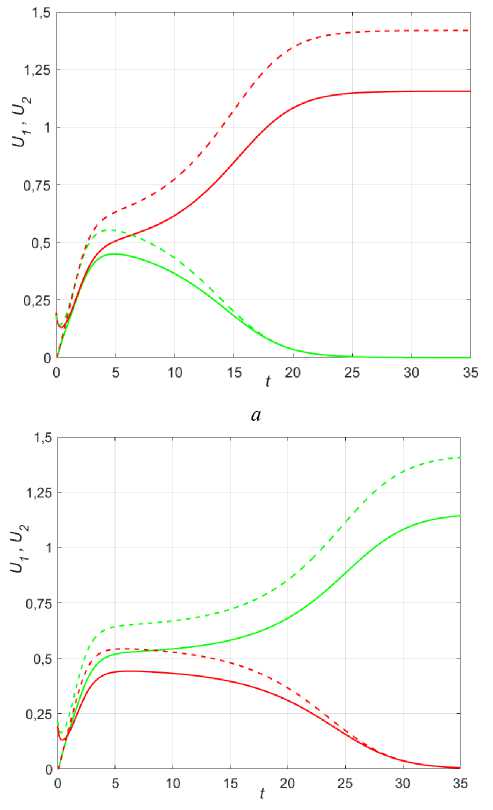
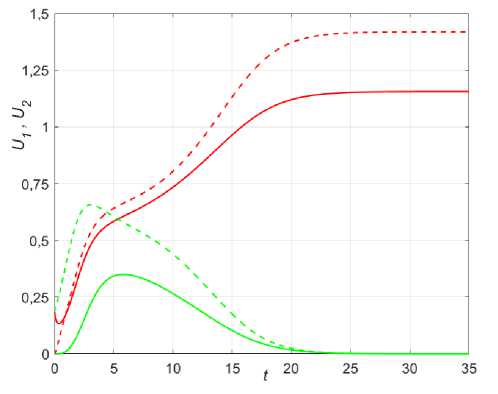
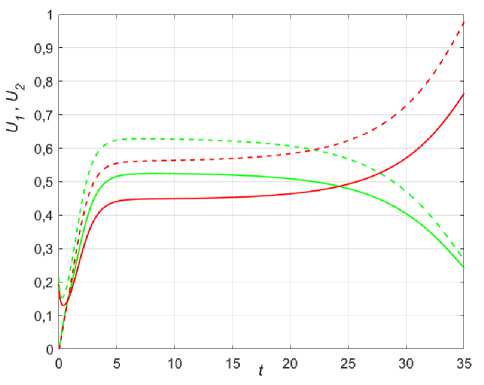
Рис. 9. Динамика различных сценариев популяций при колонизации в условиях неопределенности для двух точек x = 0,25 (сплошные) и x = 0,45 (пунктир), в 1 = 1,35; в₂ = 1,4; k = 0,01; Р ( ^х ) = 0,5 + sinn x .

а - U 10 = U 0 , е = 1; б - U 1 ⁰ = U 0 , е = 0,1; в - U 1⁰ = 0,234sin ( 6nx ) , U 2 = 0,2sin ( 6n x ) , е = 1;

г - U 0 = 0,234sin ( 6nx ) , U 0 = 0,2sin ( 6nx ) , е = 1,2