Математическая модель кинетостатического расчета плоских рычажных механизмов

DOI:

For cite

В настоящее время широко распространённые графоаналитические методы анализа во многом утратили свою актуальность, уступив место различным аналитическим методам с использованием компьютерных технологий [1-5]. Для ки-нетостатического анализа механизмов используются разнообразные компьютерные программы, в основе которых положены математические модели кинетостатического расчета. В связи с этим актуальной является разработка математической модели кинетостатического расчета плоских рычажных механизмов в форме библиотеки процедур расчета для всех двухповодковых групп Ас-сура и начального звена [2-4].

Группа Ассура первого вида

Перед обращением к процедуре, вычисляющей все усилия в кинематических парах, необходимо предварительно вычислить силы инерции, моменты от сил инерции, а также знать все внешние силы и моменты, действующие на эту группу Ассура. Расчетная схема приведена на рисунке 1 [1, 3].

Определение сил F ₂₁ и F ₃₄ . Сила F ₂₁ приложена в кинематической паре А, а сила F ₃₄ - в паре С. Тангенциальные составляющие этих сил F T и F 34 определяются по уравнениям моментов ^ M B = 0, составленных из условий равновесия второго и третьего звеньев. Направления тангенциальных составляющих этих сил примем совпадающими с положительными направлениями осей y ₂ , y ₃ .Тогда сумма моментов на втором звене в развернутом виде может быть представлена в виде

( ^Fin 2 ^{sin a} Fin 2 ^G 2 ) X 2 F in 2 cos ^a Fin 2 Y 2

+ M in ₂ + M ₂ + F ₂ sin a F ₂ X_{F 2} - F ₂ cos a F ₂ Y F ₂ (1)

—FT lab = 0 , здесь Fin2 , Min2 - сила инерции и момент от сил инерции на втором звене; F2, M2 - внешние сила и момент, действующие на второе звено; αFin2 - угол наклона силы инерции второго звена; αF2 - угол наклона внешней силы на втором звене; X2, Y2, XF2, YF2 - координаты центра масс и точки приложения силы F2 второго звена относительно точки В в абсолютной системе координат; lAB - длина звена 2.

Координаты X 2 , Y 2 , X F2 , Y F2 определяются по следующим выражениям:

X 2 = S 2 x cos ^ ₂ — S ₂ y sin ^ ₂ — l_A B cos ^ ₂;

X_F 2 = P₂ x cos ^ ₂ — P ₂ y sin ^ ₂ — l_A B cos ф ₂;

Y 2 = S 2 _xsi"n V ₂ — S ₂ y cos ^ ₂ — l_A B sin ф ₂ ;    (2)

Y F 2 = P ₂ x Sin T i — P ₂ y cos ^ ₂ — l_A B si ⁿ V ₂ ;

Формула для определения F 34 аналогична:

FT

F 34

( Fsn ^ Fin 3   ^G 3 ) X 3 — F n 3 ^CoS « Fm 3 Y 3

l CB

, M ₃ + M in ₃ + F ₃ sin a F ₃ X_{F 3} - F ₃ cos a F ₃Y_{3 (3)}

CB

Определения переменных, входящих в формулу соответствуют определениям переменных звена 2.

Нормальные составляющие F ^ 1 , F₃ ^T ₄ определяются по уравнениям типа ∑F x =0 и ∑F y =0 .

T _ ( ^Fn 2 ^{sin a} Fin 2 ^G G 2 ) ^X 2 ^- F in 2 ^{CoS a} Fm 2 ^Y 2

^F 2‘ =----------------/------------------

AB

+

^M 2 ^{+ M}in 2 ^{+ F} 2 s ^{in a} F 2 ^XF 2 ^{- F} 2 ^C os ^a F 2 ^Y 2

. (4)

l AB

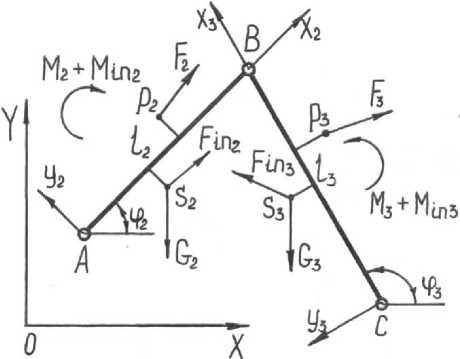
Рисунок 1. Расчетная схема группы Ассура первого вида

Запишем эти уравнения более подробно:

n              Г             П 1

F ₂₁ cos ^ ₂ + F ₂ 1 cos I ф ₂ + — I + F ₂ cos_{F 2}

i ⁿ

^{+ F} 34 cos I ^ 2 ⁺ -

+ F ₃ cos ^ ₃ + F ₃ 4 cos ^ ₃ = 0 ; (5)

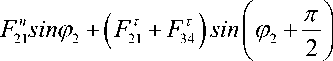
+ F ₂ sin_{F 2}

+ F ₃ sin ф ₃ + F ₃ ⁿ ₄ sin ф ₃ - G ₂ - G ₃ = 0 .

Как видно, эти уравнения являются линейными относительно неизвестных F ₂ ⁿ ₁ и F ₃ ⁿ ₄ . Решение этих уравнений получим по правилу Крамера:

где

n

b₁ cos ф ₃ b 2 sin ф ₃ cos ф ₂ cos ф ₃ sin ф ₂   sin ф ₃

COS ф ₂ Ь₁ sin ф ₂ b ₃₂

COS ф ₂ cos ф ₃ sin ф ₂ sin ф ₃

( ⁶ )

n I n 1 „

- b. = F.cos ф +   + FcOsca. +

1      21         2              2 F 2

✓ x ^V                   (7)

i ⁿ i

+ F₃ 4 cos I ф ₃ + — I + F ₃ cos a ₃ ;

n . n 1

- b ₂ = F ₂₁ sin I ф ₂ + — I + F₂sin a F ₂

. n 1

+ F ₃₄ sin I ф ₃ + — I + F ₃ cos a ₃ - G ₂ - G ₃.

n              _T I П 1

F ₂₁ cos ф ₂ + F ₂₁ cos I ф ₂ + — I + F n ₂ cos a _{Fin 2}

I n 1

⁺ F in 3 ^{COs a} Fm 3 ^{+ F} 34 ^cos I ф 2 ⁺ “ I = ⁰ ;

„              _T . n 1

F ₂₁ sin ф ₂ + F ₂₁ sin I ф ₂ + — I + F n ₂ sin a _{Fin 2}

^{+ F} 2 ^{sin a} F 2 ⁺ F in 3 ^{sin a} Fn 3 ^{+ F} 3 ^{sin a} F 3 ^{- G} 2 ^{- G} 3

Теперь можно определить F 21 и F 34 , а

также углы наклона этих сил:

F 21 =V ( F 2 - 1 ) + ( F 21 ) ;

22 ⁿ

34 ^( 34 ) ⁺( 34 ) ;

F 23 y = F 21 sin a F 21 - F in sin a Fin 2 - F 2 sin a F 2   (9)

+ g₂ .

Следовательно,

23 ^( 23 x ) ⁺( 23 y ) ;

^a F 23

= arctan

F

23 x

F

I F ²³ y I

Таким образом, найдены все 6 неизвестных для данной группы Ассура: усилия в кинематических парах А, В, С и направления этих сил.

Группа Ассура второго вида

Расчетная схема для определения усилий в кинематических парах данной группы Ассура приведена на рисунке 2 [3, 6].

Определение сил F 21 , F 34 . Расчет сил

начнем с определения силы F ^ . Эта сила опре-

деляется аналогично определению такой же силы для группы Ассура первого вида, поэтому

приводим выражение для силы F ^ ₁ без подроб-

ного объяснения:

р т _ ( F in 2 ^{sin a} Fin 2

F 21

^{- 2}) X 2 ^- F in 2 c ^{Os a} Fin 2 Y 2

l АB

M^ + M ,„ ₇ + F₂sina> Xp 1 - FxCOsa ?Y +— 2      in 2    2 F 2 F 2    2 F 2 2

.

lАB

Все переменные, входящие в это выражение, определяются так же, как и в группе Ас-сура первого вида. Силы F ₂ ⁿ ₁ и F 34 определяем

из условий ∑F x =0 и ∑F y =0 . Введем обозначения:

I n 1

^- b 1 = F 21 c ^Os I ф 2 + - I + F n 2 ^{cOs a} _Fin 2    ⁽¹²⁾

^a F 21

= arctan

^a F 34

= arctan

^{+ ф} 2 ;

FT

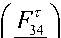
n

n

1 ^1

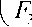
^{+ ф} 3 .

Определение величины и направления силы F 23 . Эту силу определяем из условия равновесия всех сил, действующих на звено 2. Проекции этой силы на координатные оси можно найти из уравнений:

F 23 x = F 21 c ^{Os a} F 21 - ^Fin c ^{Os a} Fin 2 ^{- F} 2 ^CO s ^a F 2 ;

+ F ₂ cOs a F ₂ + F_{in 3} cOs a _{Fin 3} + F₃cOs a F ₃ ;

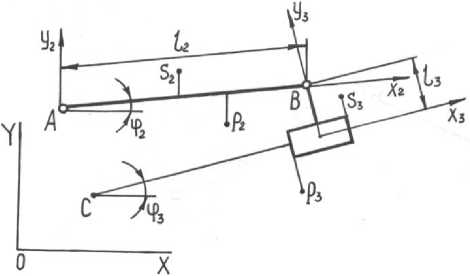
Рисунок 2. Расчетная схема группы Ассура второго вида - b 2 = F T sin | ф ₂ + П | + F n 2 sin a Fin 2 - G 2 (¹³) + F ₂ sin a F ₂ + F_{in 3} sin a _{Fin 3} + F ₃ sin a F ₃ - G ₃.

Тогда получим систему линейных уравнений для F ₂ ⁿ ₁ и F 34

здесь S 3x , S 3y , P 3x , P 3y - координаты центра масс и точки приложения силы звена 3 в локальной си-

_n I i П 1

F 21 cos ф ₂ + F 34 cos I ф ₃ + — I = b 1 ;

стеме координат, жестко связанной со звеном. Теперь определим

_n                     I n 1

F ₂₁ sin ф ₂ + F 34 sin I ф ₃ +— I = b 2 . (14)

Решение данной системы уравнений получаем по правилу Крамера:

( M 3 + M_m 3 + M )

h x =^A------------ — -       (20)

F ₃₄

n

I n b 1 cos I ф ₃ + —

I П b ₂   sin I ф ₃ + —

Определение величины и направления силы F 23 . Эту силу определяем из условия равновесия всех сил, действующих на звено 2. Проекции этой силы на координатные оси можно найти из уравнений:

^F 23 x = ^F 21 ^cos « F 21 - ^Fin 2 co ^s « Fin 2 ^{- F} 2 ^c os « F 2 ;

I . П

COS ф ₂ cos I Ф 3 + —

;

F 23y = F 21 sin « F 21 - F in 2 sin « Fin 2 - F , sin a F 2 (^2r)

+ G 2.

F 34 =

I n

Sinф2  sin I Ф3 + — cosф2   b1

sin ф ₂   b ₃₂

Следовательно,

¹ 23 (V 23 x ) ⁺( 23 y ) ;

^a F 23

= arctan

(F A

23 y

V 23 x 7

I П

COS ф ₂ cos I Ф 3 + —

Таким образом, определены все силы и

их направления в кинематических парах группы Ассура второго вида.

• I , П Sin ф ₂   sin I Ф 3 +y

Тогда

F 21 =V ( f t ) + ( f» )   ;

a_F = = arctan F 21

_F ^T 1 — + Ф ₂. n 2

-t 01

Точку приложения силы F 34 - h x определим из условия равновесия моментов

Z M c = 0 F 34 h x + M 3 + M n 3 + M ^ = 0 , (17)

где

^M ^ = ( F n 3 sin ^ Fin 3 - ^G3 ) ^X 3 - F in 3 co ^ Fin3^Y3

+ F ₃ sin a F 3 X_F 3 - F ₃ cos a _F3Y_F 3 ,    (18)

где X 3 , Y 3 , X F3 , Y F3 - определяются из следующих выражений:

X 3 = S 3 _xcos ф ₃ - ( S ₃ y - 1 3 ) sin ф ₃ ;

• Y ₃ = S _{3 x}sш ф ₃ - ( S ₃ y - 1 ₃ ) cos ф ₃ ;

X f 3 = P 3x COS ф з - ( P 3 y - 1 3 ) sin ф з ;   (19)

• ^Yf 3 = ^P 3 x^si n Ф з ^- ( ^P 3 y ^{- 1} 3 ) ^coS Ф з ,

Группа Ассура третьего вида

Расчетная схема данной группы представлена на рисунке 3 [3,7].

Сначала определим вспомогательные величины

I1

• 1    = V 1 ₂2 + 1 32 ; T = arctan — . (23)

• ^{2    3}                      V l 3 7

Определение силы F34. Данную силу определим по уравнению моментов относительно точки А, рассматривая равновесие двух звеньев: второго и третьего. Сначала определяем вспомогательные величины:

X 2 = S _{2 x}cos ф ₂ - ( S _{2 y} - 1 ₂ ) sin ф ₂;

• Y ₂ = S _{2 x}sш ф ₂ - ( S ₂ y - 1 ₂ ) cos ф ₂ ;

X f 2 = P 2 x cos ф 2 - ( P 2 y - 1 2 ) sin ф 2 ;

Y_{f 2} = P _{2 x}siW i - ( P _{2 y} - 1 2 ) cos ф ₂ ;     (24)

X ₃ = - ( S _{3 y} - 1 ₃ ) sin ф ₃ ( 1 ₃ cos ф ₃ - 1 ₃ sin ф ₃ )

^{+ S} 3 x^coS Ф з ;

Y ₃ = - ( S _{3 y} - 1 ₃ ) cos ф ₃ ( 1 ₃ sin ф ₃ - 1 ₃ cos ф ₃ ) + S _{3 x}sin ф ₃;

X_F 3 = - ( P₃ y - 1 3 ) sin ф ₃ ( 1 3 cos ф ₃ - 1 3 sin ф ₃ ) ⁺ P x cos v ₃;

Y F 3 = — ( P ₃ y — 1 3 ) cos ф ₃ ( 1 ₃ sin ф ₃ — 1 ₃ cos ф ₃ ) ⁺ P 3 x^si n ^ 3 .

Определяем моменты от сил, действующих на второе и третье звено раздельно

^M £ 2 = ( ^Fu 2 s ^{in a} Fu 2 ^{- G} 2 ) ^X 2 — ^Fu 2 ^COS « Fu 2 ^Y 2 + F ₂ sin a F ₂ X_{F 2} - F ₂ cos a F ₂ Y F ₂ + M_{u 2} + M ₂;(25)

^M £ 3 = ( ^Fu 3 ^{Sin a} Fu 3 - ^G 3 ) ^X 3 - ^Fu 3 ^{C0S a} Fu 3 ^Y 3

+ F ₃ sin a F ₃ X_{F 3} - F ₃ cos a F₃ Y_{F 3} + M u ₃ + M ₃ .

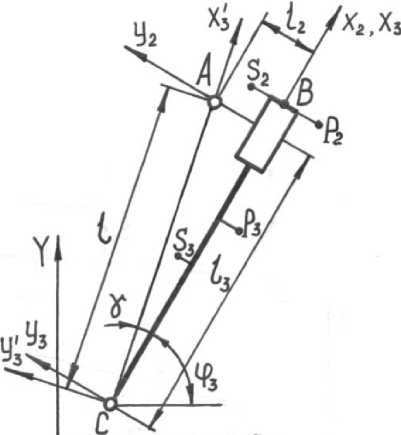
0           X

Рисунок 3. Расчетная схема группы Ассура третьего вида

Теперь можно определить F ₃ 4 и угол наклона этой силы:

£ 2 ⁺  £ 3     ,           п

F 34 = ^--—; ^a 34 = Ф 3 ⁺ Y ⁺ -. ⁽²⁶⁾

Силы F ₃ ⁿ ₄ и F ₃₂ определим из условия баланса всех сил, действующих на звено 3: ( ∑Fx=0 и ∑Fy=0 ).Отсюда имеем:

cos( ф ₂ + у )

cos I ф ₃

Q =

п

+ —

F 3 4 =

F^т = 34

^sin( ^ 2 ⁺ Y)

sin I ф ₃

1 I . п b 1 cos I ф ₃ + —

7 I , П b ₂ sin I ф ₃ + —

Q cos(ф2 + y ) b, sin(ф2 + y ) b2

где b1 = -Fin 3 cOsaFin 3

Q

,

;

- F 34 cos a F , - F ₃ cos a F ₃;

b 2 = G 3 - ^Fin 3 ^{sin a} Fin 3 - ^F3 ^T 4^{sin a} F T

- F ₃ sin a F ₃.

Таким образом, получаем:

22 ^t

¹ 34 ^( 34 ) ⁺( 34 ) ;

^a F 34

= arctan

f к T\ F 34

Fn

V 34 7

⁺ Ф 2 ⁺ Y .

Так как F 23 =-F 32 , то остается только определить величину и направление силы F 21 .

Величина и направление силы F 21 . Эти значения силы определяются по условиям: ∑Fx=0 и ∑Fy=0 для второго звена.

^F 21 x ^{+ F}in 2 c ^{os a} Fin 2 ^{+ F}2 ^{cos a} F 2

+ F ₂₃ cos a F ₂₃ = 0 ;

F 21 y + F in 2 sin a Fin 2 + F 2 sin a F 2      (30)

+ F ₂₃ sin a F ₂₃ - G ₂ = 0 ;

F 2, =V ( F 21 x ) ² + ( F 2, y ) ²;

^a F 21

= arctan

Определение h x . Точку приложения силы F 23 – h x определим из условия равенства нулю моментов сил, действующих на второе звено. Подробное определение точки приложения силы уже приводилось, поэтому ограничимся лишь окончательной формулой для определения величины h x

h x =- M : F 23 ,             (31)

где

^M = ( ^Fin 2 ^si n ^a Fin 2 ^{- G} 2 ) ^X 2 - ^Fin 2 c ^{os a} Fin 2 ^Y 2 ⁽³²⁾ + ^F 2 ^{sin a} F 2 ^X F 2 ^{- F} 2 ^{cos a} F 2 ^Y F 2 ^{+ M} u 2 ^{+ M} 2^.

Группа Ассура четвертого вида

Схема расчета усилий в кинематических парах группы Ассура четвертого вида представлена на рисунке 4 [3]. Введены следующие определения: s 2 , s 3 , p 2 , p 3 - центры масс и точки приложения сил соответствующих звеньев данной группы Ассура.

П =

L . пA cos ф9 + к 2 J

I.. . п A cos Ф + к 21

sin

п

^ 2 ⁺ -

sin

п ^{ф +} -

Получаем решение:

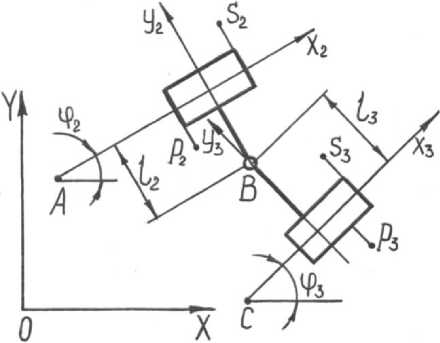
Рисунок 4. Расчетная схема группы Ассура четвертого вида

Определение F ₂₁ и F ₃₄ . Эти величины

определяются по условию баланса всех сил, действующих на группу Ассура:

I п A

^F21 cos I ^ 2 + - I + ^F _te 2 cOS « Fin 2 + F 3 cos ^ Fin 3

+ F₂ cos a F ₂

+ F₃ cos a F 3

+ F 34 cos

п

= 0;

^F 21

F 34 =

I п b 1 cos I ф ₃ + —

I п b 2 s ⁱⁿ I Ф 3 + -

П

cos

I п A sin I ф ₂ + — I b ₂

П

;

.

Определение величины и направления силы F ₂₃ . Проекции силы F ₂₃ на координатные оси можно получить из условия баланса всех сил на оси координат для звена 2:

F ₂₃ , = - F₂cos a _{Fin 2} - F₂cos a F ₂ - F ₂₁ cos a F ₂₁ ;

F₂₃ y = G 2 - F₂₁ sin a F ₂₁ - F_{in 2} sin a F ₂    (36)

- F ₂ sin a F ₂ .

Следовательно

23 ^( 21 x ) +( 23 y ) ;

F 21 sin I ^ 2 + П L F 2 ^s i_n ^a Fn 2

^a F 23

= arctan

+ F 2 sin a F 2 (33)

⁺ F n 3 ^{sin a} Fin 3 ^{+ F} 3 ^{sin a} F 3 - G 2 - ^G 3

I п ]

+ F 34 sin I ф ₃ + — I = 0.

Обозначим b1 =-( Fin 2 cOsaFin 2 + F2 cOsaF 2 + Fin 3 cOsaFin 3 +

^{- Ь} 2 = ^Fin 2 ^{sin a} Fin 2 ^{+ F} 2 c ^{Os a} F 2 ^{+ F}in 3 s ^{in a} Fin 3

+ F₃sin a F ₃ - G ₂ - G ₃;

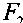
к.¹ 23 x 1

Определение точки приложения силы F 23 – h x1 . Эта величина определяется по балансу моментов, действующих на звено 2. Предварительно определим вспомогательные величины

X 2 = S 2 _xcos ф ₂ - ( S _{2 y} - 1 ₂ ) sin ф ₂ ;

• Y 2 = S 2 _xsi'n ф ₂ - ( S ₂ y - 1 ₂ ) cos ф ₂ ;

X f 2 = P 2x Cos ф 2 - ( P 2 y - 1 2 ) sin ф 2 ; (38)

• Y F 2 = P _{2 х}^1^пФ₂ - ( P _{2 y} - 1 ₂ ) cos ф ₂ ;

M 2 _Z = M_m 2 + M 2 ( F in 2 sin a F _m 2 - G 2 ) X 2

- F_in 2 cos a _{Fin 2} Y ₂ + F ₂ sin a F ₂ X_{F 2} - F ₂ cos a F ₂ Y F ₂

Тогда hx 1 = M 2£ : F21 .

Определение точки приложения силы F 34 – h x2 . Определение аналогично определению h x1 .

Y₃ = S _{3 x}sin ф ₃ — ( S _{3 y} — 1 ₃ ) cos ф ₃ ;

^XF 3 = ^P 3 х^СО5 Ф 3 ^— ( ^P 3 y ^{— 1} 3 ) s ⁱ n Ф з ;

Y f 3 = P 3 x Sin Ф з — ( P 3 y — 1 3 ) cos ф з ;    (40)

Рисунок 5. Расчетная схема группы Ассура пятого вида Введя обозначения:

^bi = ^— ( F in 3 ^{cos a} Fin 3 ⁺ F 3 ^{cos a} F 3 ) ;

b 2 = — ( F in ₃ sin a Fin ₃ + F ₃ sin a F ₃

^

G 2 — G 3 ) ;(43)

I n 1             n cos I Ф2 + — I cos I Ф3 + —

E =

.

I ⁿ 1 I ⁿ sin I Ф ₂ + — I   sin I Ф 3 + —

M 3 ^ = ^Min 3 ⁺ M 3 ( F in 3 s ^{in a} Fin 3

^{— F}in 3 ^{cos a} Fin 3 ^Y 3 ^{+ F} 3 ^{sin a} F 3 ^XF 3

^{— G}3 ) ^X3

— F ₃ cos a F ₃ Y F ₃.

Тогда

h = -M ■ R h x     M ₃ ^ : F 34 .

Группа Ассура пятого вида

Расчетная схема данной группы представлена на рисунке 5 [3]. На рисунке введены обозначения: S 2 , S 3 , р 2 , р з - центры масс и точки приложения сил второго и третьего звеньев.

Определение значений сил F 21 и F 34 . Величины определяются по условию баланса всех сил, действующих на группу Ассура:

I П 1

F 32 cos I Ф 2 + - I + F in 3 ^{cos a} Fin 3 ^{+ F} 3 ^{COs a} F 3

I n 1

+ F 34 cos I ф ₃ + — I = 0 ;

I П I

F 32 sin I Ф 2 + - + ^Fn 3 sin a Fin 3 ^{+ F} 3 ^sin « F 3

^{— G} 2

—

G 3 + F 34 sin I Ф 3

П I

+    = 0 .

2 }

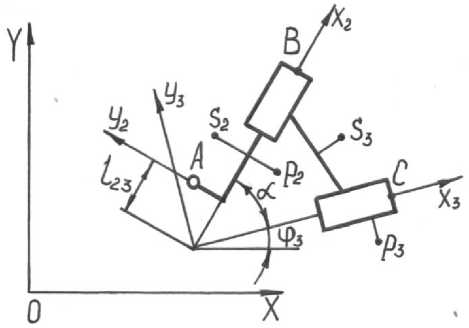
Получаем решение:

I n b1 cos I ф3 + —

I n b ₂   sin I ф ₃ + —

R

cos

E

;

^si n I Ф 2 ⁺tI ^b2

F 34 =

E

.

Определение h x1 и h x2 . Определим в начале вспомогательные величины

F 23 =F 23 ;

α F23 = α F23 +π ;

X 2 = S 2 _xcos ф ₂ — ( S ₂ y — l ₂ ) sin ф ₂ ;

Y ₂ = S _{2 x}si'n ф ₂ — ( S ₂ y — 1 ₂ ) cos ф ₂ ;

^XF 2 = ^P2 x^COS Ф 2 ^— ( ^P 2 y

^YF 2 = ^P 2 x^Sin Ф 2 ^— ( ^P 2 y

—

—

l 2 ) sin ф ₂ ;    (45)

l 2 ) cos ф ₂ ;

M 2 _Z= M in 2 + M 2 — ( F n 2 sin a Fin 2

^{— G} 2 ) ^X 3

— F in 2 cos a Fin 2 Y 2 + F 2 sin a F 2 X f 2

— F ₂ cos a F ₂ Y_{f 2} .

Тогда:

h x =— M 2 _Z : F 23 ;

X ₃ =— S _{3 y}si ⁿ Ф 3 — ( 1 ₂₃ cos ф 2 — 1 ₂ sin ф 2 ) + S _{3 x}cos ф ₃ ;

Y ₃ = S _{3 y}cos ф ₃ — ( 1 ₂₃ sin ф ₂ + 1 ₂ cos ф ₂ ) + S _{3 x}sin ф ₃ ;

X_{F 3} = — P _{3 y}si'n ф ₃ — ( 1 ₂₃ cos ф ₂ — 1 ₂ sin ф ₂ ) + P_{3 х}со&ф₃;

Y F 3 = P_3ycos ф ₃ — ( 1 ₂₃ sin ф ₂ — 1 ₂ cos ф ₂ ) + P_3xsi^n ф ₃ ;

^M 3 ^ = M in 3 ^{+ M} 3 ( ^Fin 3 ^{sin a} Fin 3

^X 3 ^{— F}in 3 ^{COs a} Fin 3 ^Y 3

—

G 3 )

+ F₃sin a F3 X_F 3 — F₃cos a F ₃Y_F 3 .

Тогда:

M у + M y h x =--^ ;         (47)

F 34

• ^F21 x =- ^F 2 cos ^a F 2 - ^Fin 2 ^C0S « Fin 2 - F 23 c ^0S « F 23 ;

F_{21 y} = G 2 - F in 2 sin a Fin 2 - F 2 sin a F 2 - F ₂₃ sin a F23

Тогда

F 2i ⁼ V( F 21 x ) + ( F 21. У ) .         (48)

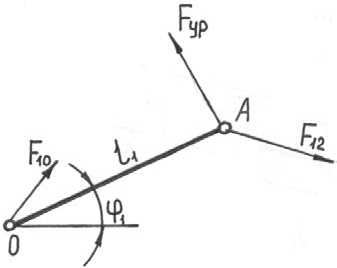
Рисунок 6. Расчетная схема начального звена

Начальное звено

Схема распределения сил, действующих на начальное звено, представлена на рисунке 6 [3].

Определение F ур . Определение этой силы производится по уравнению ∑M A =0 . Сначала определяем вспомогательные величины:

X 1 =l 1 cosφ 1 ;    Y 1 =l 1 sinφ 1 ;

F 12x = F 12 cosα F12 ; F 12y = F 12 sinα F12 .  (49)

Тогда:

Примечание. Если определяется кинетостатика механизма с параллельным закреплением двух групп Ассура на начальном звене, то в этом случае сила F12 является геометриче- ской суммой сил, действующих на начальное звено со стороны отброшенных групп Ассура. Ее определение не вызывает трудностей:

• ^F12x = ^F12^{C0S a} F 12 ^{+ F} 14 ^{C0S a} F 14 ;

  F 12 y

  
  

_ F₁₂sin a F ₁₂ + F₁₄sin a F ₁₄ .

F _ ^J 12 x -*1   ' 12 y ^{v L}1

F УР =          z l1

П и aFyp = Ф1 + ~ . (50)

Тогда

Определение величины и направления силы F 10 . Эти значения определим из условия равенства нулю всех сил, действующих на звено 1.

F 2 ⁼V ( F 2 x ) ² + ( F y ) 2 ;

^a F 12

_ arctan

F

V 12 x 7

Тогда

^F 10 x ^{_- ( F}yp^{C0S a} Fyp ^{+ F} 12 x ) ;

^F 10 y ^{_- ( F}yp^{Sin a} Fyp ^{+ F} 12 y ) . ⁽⁵¹⁾

F 0 _ V ( F o x ) 2 + ( F 0 , ) ²; .

здесь F 12 - сила, действующая на начальное звено от первой группы Ассура; F 14 - сила, действующая на начальной звено от второй группы Ассура.