Математическая модель клеточных преобразований при регенерации костной ткани в условиях изменяющейся биохимической среды с возможной механорегуляцией

Теме моделирования процесса восстановления кости посвящены многочисленные работы. Особое внимание в них уделяется исследованию отношений между механической стимуляцией и преобразованием клеток и клеточных структур в процессе регенерации кости. Наиболее полноценной и адекватной для достижения целей управления механической стимуляцией процессов заживления костных тканей авторы считают модель, предложенную в [16]. Теоретическое исследование восстановления механических свойств ткани в зоне перелома с использованием осесимметричной конечно-элементной модели фрагмента кости было проведено с помощью уравнения диффузии, описывающего пространственно-временное распределение концентрации мезенхимальных стволовых клеток.

В работе [13] указывается на необходимость исследовать процессы миграции, пролиферации и дифференциации клеток различных типов. Предложенная в [13] модель была разработана для описания изменения концентраций фибробластов, хондроцитов и остеобластов, а также временного и пространственного распределения фиброзной (соединительной), хрящевой и костной тканей. Деятельность четырех типов клеток: мезенхимальных стволовых клеток, фибробластов, хондроцитов и остеобластов, взаимодействующих в зависимости от механической стимуляции, характеризовалась преобразованием друг в друга и в структуры тканей.

Кроме статьи [13], развивающей диффузионную модель [16] распространения активных протоклеток в область костной мозоли, возникающей после перелома, стоит упомянуть современные исследования, посвященные влиянию так называемых факторов роста на процессы биохимических преобразований мезенхимальных стволовых клеток в дифференцированные типы клеток [27, 28] при регенерации костной ткани. В данных работах подчеркивается их значительное стимулирующее влияние на пролиферацию, миграцию и дифференциацию клеток во время заживления кости. Можно отметить на основе собственных исследований [3, 19], что без учета факторов роста, активирующих процессы движения и преобразования клеток, представляется проблематичным построение адекватной модели, корректно описывающей восстановление костной ткани в объеме скаффолдов, применяемых в тканевой инженерии для замещения крупных дефектов длинных трубчатых костей человека. Нормальные значения скоростей процессов миграции, дифференциации и пролиферации клеток, используемые в модели регенерации костной мозоли [13, 16], без биохимического стимулирования могут оказаться недостаточными для заполнения клеточным материалом порового пространства имплантата значительного размера.

Математические модели, описывающие процессы преобразования клеток, в первую очередь дифференциацией мезенхимальных стволовых клеток, не ограничиваются только дифференциальными уравнениями типа приведенных в [13]. Активно развиваются как детерминистские цепные модели [21, 30], так и стохастические подходы [22] на их основе.

Уточнению модели [13, 16] были посвящены работы, учитывающие дополнительные ключевые аспекты заживления перелома кости, такие как направленная миграция клеток и развитие сети кровеносных сосудов [10, 23]. Действительно, существует тесная взаимосвязь между временем репарации кости и формированием кровеносных сосудов [9, 29]. Восстановление кровоснабжения признается важнейшим компонентом регенерации кости в работах [11, 24]. В [25] указывается, что рост новых капилляров кровеносных сосудов и формирование зрелой сосудистой сети имеют большое значение для дифференциации клеток в остеобласты и формирования костной ткани.

В настоящей работе будет рассмотрено обобщение предложенных в [10, 13] подходов к описанию процессов миграции клеток на основе уравнения диффузии в одномерном случае [3], клеточным преобразованиям и возникновению дифференцированных типов тканей с введением в рассмотрение моделей факторов роста.

Математическая модель преобразования клеток и тканей

Будем рассматривать диффузионную модель, учитывающую миграцию, пролиферацию, дифференциацию и апоптоз следующих восьми типов клеток и тканей, для которых введем сквозную нумерацию. Во-первых, четырех типов клеток: 1) мезенхимальных стволовых; 2) фибробластов; 3) хондроцитов; 4) остеобластов. Во-вторых, четырех типов тканей: 5) фиброзной (соединительной); 6) хрящевой; 7) костной и 8) кровеносных сосудов.

Перейдем к описанию предлагаемой математической модели восстановления кости, представляемой как динамический процесс установления нормальных концентраций (т.е. концентраций, присущих здоровой кости) для указанных выше восьми типов клеток и тканей, i = 1...8.

Будем рассматривать кость как цилиндр длины l по оси x с постоянным поперечным сечением. Предполагается, что все характеристики кости усреднены по поперечному сечению и зависят только от положения сечения на отрезке [ 0, l ] и времени t >  0. Пусть начальный момент t = 0 соответствует повреждению кости, возникающему, например, в результате механической травмы, перелома кости или болезни.

Ограничимся рассмотрением указанных выше восьми основных типов i = 1...8 клеток и тканей (для краткости будем писать «клеток»), составляющих кость. Через c ( х, t ) обозначим объемную концентрацию клеток i- го типа в поперечном сечении х в момент t. Пусть c ( х ) - концентрация клеток i- го типа в неповрежденной кости в поперечном сечении х. Будем считать эту концентрацию известной при любом i = 1...8 на всем отрезке [ 0, l ] и для определенности будем называть ее нормальной; в [13] указаны максимальные концентрации различных типов клеток, и в качестве нормальной концентрации клеток того или иного типа в первом приближении можно взять половину от их максимальной концентрации.

Пусть [a, b] - зона повреждения кости по ее длине, [c, d ] - возможно, несколько более широкий участок, на котором явно выражено влияние зоны повреждения и может образоваться костная мозоль (0 < c < а < b < d < l). Начальная концентрация уг (х) клеток i-го типа рассматривается как сумма соответствующей нормальной концентрации  c (х)  и некоторой вызванной повреждением кости возмущающей функции ^. (х), где ^. (х) равна 0 вне отрезка [ c, d ], носит хаотический d нерегулярный характер на [c, d ] и удовлетворяет неравенству J ^ (х) dx < 0, c отражающему возможность потери костного материала во время повреждения кости.

Будем считать, что концы х = 0, х = l цилиндра, моделирующего кость, и его боковая поверхность на участке [ c, d ] полупроницаемы, что свидетельствует о действии закона Ньютона для диффузии клеток каждого типа, т.е. поток внутрь объема цилиндра пропорционален разности между концентрациями этого типа клеток в среде и на соответствующих участках поверхности цилиндра. В результате получаем неоднородные граничные условия третьего рода в сечениях x = 0, x = l, а для участка [c, d] в правой части основного уравнения возникает дополнительное слагаемое.

Отметим, что в случае, когда коэффициент проницаемости стенок в сечениях x = 0, x = l обращается в 0 (случай непроницаемости кости в граничных сечениях), мы получаем однородные граничные условия второго рода.

Будем полагать, что на боковую поверхность кости на участке [c, d ] не попадают клетки окружающих мягких тканей и не происходит прорастания соединительной ткани в пустоты, возможно имеющиеся в кости в результате механического повреждения, с последующим образованием рубцовой ткани, препятствующей нормальной регенерации кости. Для достижения этой цели при определенных обстоятельствах может быть поставлена остеоиндуктивная искусственная мембрана, отделяющая поврежденную поверхность кости на участке [c, d ] от окружающих мягких тканей, но пропускающая необходимые для регенерации кости клетки. Кроме того, эта мембрана также защищает поврежденные участки кости от возможных локальных механических повреждений в процессе регенерации, а также она может при необходимости являться носителем морфогенетических белков и других факторов роста, способствующих росту клеток типов 1…4 и наносимых на внутреннюю поверхность мембраны. Важно, что этим процессом доставки морфогенетических белков можно управлять. Возможность этого также учитывается в рассматриваемой модели.

Выпишем основную систему восьми уравнений (1) относительно восьми неизвестных функций c ( x, t ) :

d c d t

a 2c(

= D, — + afc1 i ax2

+Z f j * i

1-cL  -a“Pci + ku (Фi 1 (x, t) -ci)X[c,d] (x),

c t > 0,  0 < x < l, i = 1...8.

Здесь Df - коэффициент диффузии; af (t) - функция, определяющая интенсивность пролиферации клеток; c – нормальная концентрация клеток i-го типа в кости; a^f (t) - функция, определяющая интенсивность дифференциации i-го типа клеток в j-й; a“p (t) - функция, определяющая интенсивность апоптоза клеток i-го типа;

k – коэффициент интенсивности проникновения клеток i-го типа из внешней среды (например из надкостницы) через боковую поверхность кости на участке [ c, d ]; Фп (x, t) - концентрация клеток i-го типа вне кости вблизи от ее поверхности; X[c dj(x) - индикатор, принимающий значение 1, если x из [c, d], и значение 0 в противном случае. Величины apr , adiff , aap являются неотрицательными функциями, зависящими от времени t, а также от некоторых биохимических и механических факторов роста, в различной степени стимулирующих процессы пролиферации, дифференциации и апоптоза рассматриваемых типов клеток и количественно также зависящих от времени t . Умножение adiff на c в правой части уравнения (1) означает, что скорость процесса дифференциации клеток типа j , отличного от i , в клетки типа i , пропорциональна имеющейся концентрации клеток типа j . При этом умножение на

c относительный множитель 1 —L  обеспечивает уменьшение этой скорости при ci приближении концентрации c клеток типа i к их нормальной концентрации c . Знак

«плюс» перед слагаемым

diff a ji cj

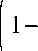
cL ci)

показывает, что такая дифференциация

способствует увеличению концентрации клеток типа i. Аналогично объясняется вид всех других слагаемых в правой части (1). В предпоследнем слагаемом правой части

c

(1), описывающем процесс апоптоза клеток типа г, множитель 1 —L отсутствует, ci поскольку этот процесс обусловлен генетически и его скорость не зависит от близости концентрации c к концентрации c .

Подчеркнем, что при значениях индекса i = 5, 6, 7, 8 уравнения (1) определяют закон изменения плотностей тканей в результате возникновения и преобразования клеток соответствующих типов. При этом все коэффициенты диффузии должны быть равными нулю. Коэффициент, характеризующий апоптоз ткани, также обращается в нуль: a“p (t) = 0, в то время как два других коэффициента - app (t) и adf (t) - понимаются как функции, определяющие интенсивность процессов роста и деградации массы (плотности) соответствующих костных структур.

Граничные условия третьего рода (2) для концентраций четырех типов клеток и начальные условия (3) для всех типов клеток и тканей примут следующий вид:

^C.

t >  0, i = 1...4,

t > 0, i = 1...4, i = 1...8.

- D i Dx ( ⁰ t ) ^{+ k} 2 ( c i ( ⁰ t ) - Ф i ² ( t ) ) = ⁰,

^C.

Di ~T ( ^l , t ) ^{+ k} 2 ( ci ( ^l, t ) - Ф i 2 ( t ) ) = ⁰, d x

C ( x ,0 ) = y_z ( x ) ,     0 <  x <  l,

Отметим, что k – это коэффициент проницаемости клеток i-го типа из внешней среды внутрь кости через полупроницаемые граничные сечения x = 0 и x = l, а ф;2 (t) – концентрация клеток i-го типа во внешней среде вблизи этих граничных сечений. Стенки x = 0 и x = l становятся непроницаемыми при равенстве нулю коэффициента диффузии D = 0. Заданные функции ф; (x) соответствуют характеру разрушения тканей и определяют распределение концентраций клеток и плотности тканей в начальный момент времени.

Установить явный вид функций ф_;2( t ) , ф_п ( x, t ) можно только в хорошо поставленном натурном эксперименте. При численном анализе для простоты и без потери общности можно задавать их равными константами, значения которых подбираются из виртуального эксперимента при многократном запуске модели для достижения наибольшего соответствия результатов расчетов реальному положению дел.

Очевидно, что система дифференциальных уравнений (1) содержит большое количество коэффициентов. Многие из этих параметров, в частности постоянные значения коэффициентов диффузии, скоростей процессов дифференциации, пролиферации и апоптоза клеток и соответствующих тканей, максимальные значения концентраций клеток и тканей, приведены в [13] на основе глубокого анализа реферативных данных. Они могут быть использованы при решении системы (1) для моделирования регенерации ткани в области костной мозоли, возникающей при переломе кости вблизи поверхности имплантатов. Однако, как было отмечено во введении, в случае замещения дефектов кости пористыми скаффолдами значительных размеров постоянные значения интенсивностей a pr , a diff , aap вряд ли подходят и могут приводить к неверным результатам, поскольку не учитывают биохимическую стимуляцию регенерации с помощью факторов роста. Конечно, и в других случаях лечения повреждений костей при использовании факторов роста вид коэффициентов системы (1) нуждается в уточнении. Поэтому следующие разделы статьи будут посвящены разработке коэффициентов системы как временно-зависимых функций, учитывающих биохимическую и механическую стимуляцию.

Описание биологических факторов роста

Регенерация костной ткани после повреждения представляет собой ряд последовательных стадий, включающих разрушение всех основных структур кости с формированием гематомы между отломками, воспалением и пролиферацией костной ткани, формированием соединительнотканной мозоли с последующей ее минерализацией и перестройкой [1, 27].

Каждая стадия сопровождается изменением концентрации биологически активных веществ и клеток в регенерате. Так, повреждение кости приводит к вазоконстрикции и снижению регионарного кровотока до 50 %. Данная физиологическая реакция направлена на снижение объема потери крови и уменьшение формирующейся гематомы. Сама гематома инициирует каскад биологических реакций, направленных на увеличение проницаемости сосудов и увеличение концентрации медиаторов воспаления и цинокинов, таких как TNF-α, IL-1, IL-6, IL-11, IL-18, Ang-1, Ang-2. Это позволяет привлечь в зону регенерации полиморфно-ядерные лейкоциты, макрофаги, мезенхимальные стволовые клетки, начать прорастание новых капилляров, которые, в свою очередь, формируют сеть фибриновых, ретикулярных и коллагеновых волокон, стабилизирующих отломки.

Воспалительная реакция также инициирует активность остеокластов, которые удаляют некротизированные участки кости, подготавливая последнюю к заживлению. В последующем гематома видоизменяется в грануляционную ткань, являясь частью «мягкой» костной мозоли. Постепенно в регенерате повышается концентрация биологически активных веществ, направленных на образование хрящевой мозоли (TGF- β 1, TGF- β 2, TGF- β 3, GDF-5, BMP-5, BMP-6, IGF-1) путем пролиферации и дифференцировки мезенхимальных клеток. В последующем повышается концентрация биологических факторов роста (VEGF, BMP-2, TNF-α), позволяющая сформировать незрелую грубую волокнистую костную ткань, которая в дальнейшем подвергается ремоделированию под влиянием механической среды.

Таким образом, процесс восстановления костной ткани после повреждения можно рассматривать как сложный взаимосвязанный каскадный биологический механизм, включающий остановку кровотечения, удаление омертвевших остатков костной ткани, привлечение в зону регенерата клеток, участвующих в восстановлении механической целостности и прочности поврежденной кости с последующей ее перестройкой. Можно сказать, что имеет место тонкая настройка структуры костного вещества в зависимости от механической нагрузки в каждой конкретной точке поврежденной кости. Это, в конечном итоге, позволяет вновь интегрировать поврежденный участок в общую структуру скелета. Маркерами начала и окончания той или иной фазы можно считать изменение концентрации биологически активных веществ и клеток.

В табл. 1 приведены основные типы биохимических факторов роста, стимулирующих соответствующие стадии регенерации костной ткани.

Морфогенетические белки кости – это совокупность факторов роста кости, появляющихся только при объемных травмах и переломах. Это белковые молекулы-магниты TGF-β, притягивающие клетки кости в точки, нуждающиеся в восстановлении. Морфогенетические белки кости проходят три главных этапа последовательно с костным морфогенезом, а именно, хемотаксис, размножение и дифференциацию временной хрящевой основы, а также постоянную костную индукцию.

Внеклеточный белок TNF-α является многофункциональным провоспалительным цитокином, синтезирующимся в основном моноцитами и макрофагами. Влияет на липидный метаболизм, коагуляцию, устойчивость к инсулину, функционирование эндотелия. Трансформирующий ростовой фактор бета TGF-β S – белок, который контролирует пролиферацию, клеточную дифференциацию и другие функции в большинстве клеток. Инсулиноподобный фактор роста IGF-1 – белок из семейства инсулиноподобных факторов роста, по структуре и функциям похожий на инсулин. В его функции входит эндокринная, аутокринная и паракринная регуляция процессов роста, развития и дифференциации клеток и тканей организма.

Влияние факторов роста на биологические процессы

Таблица 1

Фактор роста	Стадия воспаления	Хондрогенные процессы (образование хрящевой ткани)	Образование и формирование костной ткани	Кровеносные сосуды
BMP	Ограничение воспалительного процесса (TNF-α)	Морфогенез хряща, влияние на скелетные модели. Пролиферация и созревание хондроцитов, сильная индукция хондрогенной дифференциации мезенхимальных клеток	Развитие миграции клеток, пролиферация и остеогенная дифференциация мезенхимальных клеток (BMP-2, TNF-α) [6, 8, 14, 17]	–
TGF-β S	Миграция коллагена, остеонектина и остеопонтина, стимуляция недифференцированных мезенхимальных клеток [17, 20]
	–	Повышение пролиферации хондроцитов. Стимуляция хондрогенной дифференциации мезенхимальных клеток	Ингибирование пролиферации зрелых клеток и предшественников остеокластов [8]	Стабилизация новых кровеноc-ных сосудов
IGF-1	Посредник воспаления	Хондрогенная дифференциация мезенхимальных стволовых клеток	Производство костного матрикса [7]. Стимулирующие эффекты образования остеобластов [14]	–
VEGF	–	–	Обеспечение миграции и дифференциации остеобластов [12]	Формирование транспорта крови [6, 11, 14], развитие сосудов

Эндотелиальный фактор роста сосудов VEGF – еще один из членов семейства структурно близких между собой белков. Он влияет на развитие новых кровеносных сосудов (ангиогенез) и выживание незрелых кровеносных сосудов (сосудистая поддержка), связываясь с двумя близкими по строению мембранными тирозинкиназными рецепторами и активируя их.

Математические подходы к моделированию факторов роста

Анализируя концентрацию факторов роста по данным, полученным в [15, 18, 26] и [27], можно выдвинуть следующую гипотезу. Поступление факторов роста в область повреждения кости подчиняется некоторому генетическому закону, который выделяет в зону повреждения количество фактора роста, необходимое для реализации процесса роста. При этом в нормальных условиях жизнедеятельности кости генерация факторов не ограничена в тех объемах, которые необходимы для процесса восстановления тканей, миграции, пролиферации и дифференциации клеток. Следовательно, можно предположить, что мы имеем простейшую модель распределения моментов поступления факторов роста в зону повреждения, известную в теории очередей как многоканальная система массового обслуживания со стационарным однородным потоком заявок, т.е. моментов поставки в зону «порции» соответствующего фактора роста [5]. В этом случае зависимость концентрации фактора роста от времени Ф. ( t ) необходимо рассматривать как функцию Эрланга вида

Ф j ( t ) = f_f t n - e - ^{T jt} , (4)

где f, n, Tj - параметры функции, отвечающей j - му фактору роста, которые выбираются так, чтобы экспериментальные наблюдения были наиболее близки к значениям ФД t ) .

На основе простейшей схемы оптимизации с использованием метода наименьших квадратов были получены аналитические выражения концентрации факторов роста, влияющих на развитие и подавление воспалительного процесса, процесса образования хрящевой ткани, процесса образования и формирования костной ткани. Рассчитанные параметры функций Эрланга представлены в табл. 2, а функциональные асимптотики соответствующих факторов роста – на рис. 1.

Таблица 2

Процесс образования и формирования костной ткани

№ п/п	Процесс, аппроксимирующая функция	Участие факторов роста	Рассчитанные параметры модели			Достоверность (коэффициент детерминации)
			f j	n j	τ j
1	Воспалительный, Ф 1 ( t )	TNF-α, IGF-1	16,663	2,3	2,875	0,685
2	Образование хряща, Ф 2 ( t )	TGF-β S , BMP-5, BMP-6, IGF-1	0,00082	7	0,9333	0,845
3, 4	Окостенение (образование кровеносных сосудов), Ф 3 ( t ) , Ф 4 ( t )	VEGF, BMP-2, TNF-α	0,0028	3,5	0,2413	0,615

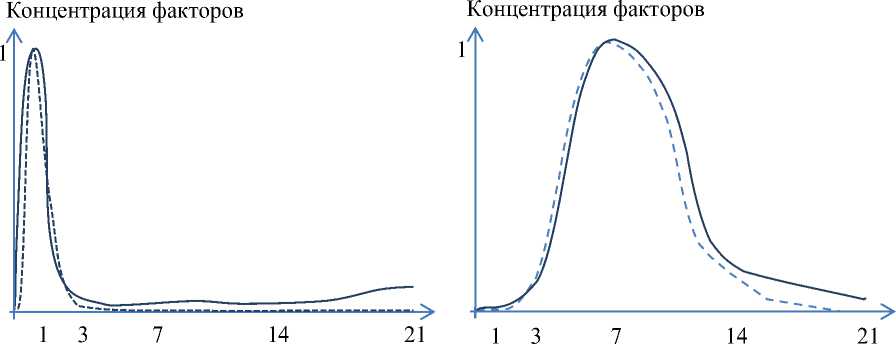
Время, день                              Время, день

_{Воспалительный процесс}                    Концентрация факторов TGF-β S ,

Функциональная асимптотика Ф 1 ( t )           ^{BMP-5, BMP-6, IGF-1}

Функциональная асимптотика Ф 2 ( t )

а                                         б

Концентрация факторов

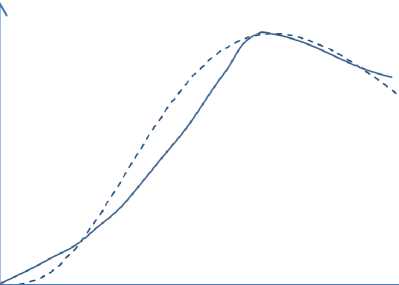
1   3       7           14            21

Время, день

Концентрация факторов VEGF, BMP-2, TNF-α на стадии окостенения Функциональная асимптотика Ф 3 ( t )

в

Рис. 1. Модель динамики концентрации факторов роста, влияющих на развитие и подавление воспалительного процесса ( а ), на процесс образования хрящевой ткани ( б ), на процесс образования и формирования костной ткани ( в )

Все функции Эрланга построены таким образом, чтобы их максимальные значения были равны единице. Тем самым нормированные на единицу функции Эрланга используются для задания временной зависимости, в то время как абсолютные значения представим с помощью масштабных коэффициентов (см. следующий параграф).

Процесс активного построения кровеносных сосудов, на который существенное влияние оказывает фактор VEGF, нами рассматривается как совпадающий с процессом образования и формирования костной ткани, что позволяет принять равенство ^Ф 4 ( t ) = ^Ф 3 ( t ) ^.

Описание параметров модели

Рассмотрим функциональные зависимости между параметрами системы уравнений (1). Четыре первых уравнения системы описывают миграцию, пролиферацию, дифференциацию и апоптоз каждого из основных типов клеток i . Движение клеток в ткани моделируется с помощью диффузионного процесса. Предполагая, что изменения коэффициентов D , k и k будут несущественны, положим их равными константам. В случаях i = 5, 6, 7, 8 имеем Д = 0, так как миграция сформированных тканей, естественно, отсутствует. В этих случаях к_п = 0, k_j2 = 0, так что первое и последнее слагаемые в правой части (1) и граничные условия (2) пропадают, а знание функций ф_;2 ( t ) , ф_;, ( x, t ) не требуется.

Скорость изменения концентрации исследуемых клеток пропорциональна количеству фактора, инициирующего изменение этой концентрации. Кроме того, так как концентрация ограничена «нормальным» значением c , процесс должен стабилизироваться около c . Следовательно, вклад влияния пролиферации на скорость д c изменения концентрации i можно оценить как д t a pr

( t ) c i  ¹

—

ci

c

Аналогично для дифференциации одного типа клеток в другой можно получить упрощенные формулы. В частности, если i -й тип преобразуется в j -й, то вклад в изменение скорости концентрации можно оценить как diff aij

( t ) ^c i 1 ^— j .

c

Наоборот, если j -й тип преобразуется в i -й, то вклад в скорость изменения концентрации примет вид

, ( t ) c 1 —

V ci 7

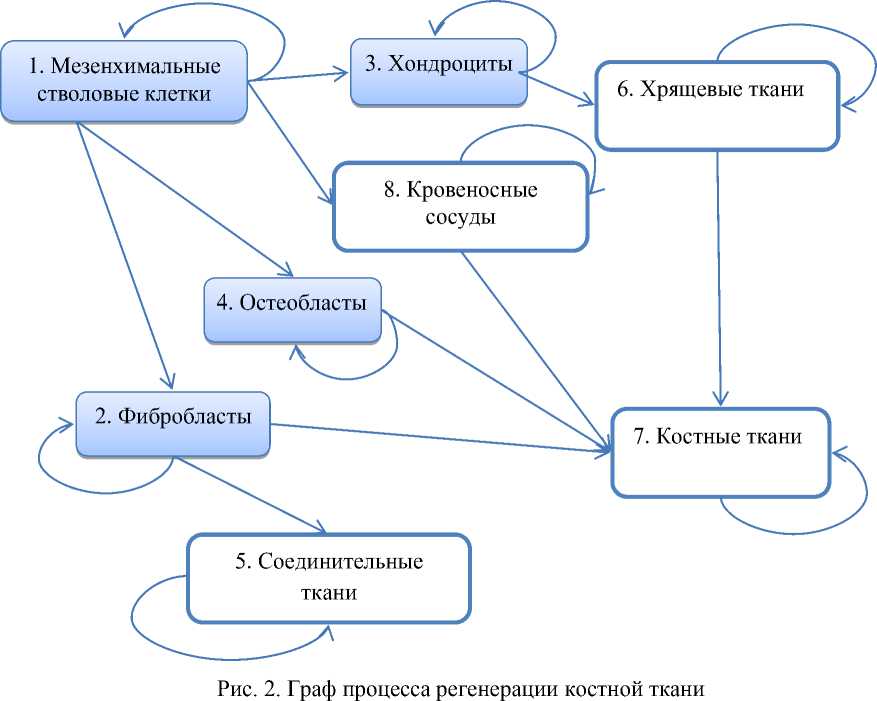
Рассмотрим схему, описывающую развитие костной ткани. На графе (рис. 2) выделены следующие состояния развития: 1) мезенхимальные стволовые клетки; 2) фибробласты; 3) хондроциты; 4) остеобласты; 5) соединительные ткани; 6) хрящевые ткани; 7) костные ткани и 8) кровеносные сосуды.

Стрелки, представляющие собой ориентированные ребра, соединяющие разные вершины, означают, что возможны дифференциация одного типа клеток в другой или преобразование (структурирование) клеток в ткань. Наличие петлеобразных стрелок, выходящих и входящих в одну вершину, указывает на процесс пролиферации или развития структуры.

В рассматриваемой математической модели каждому ребру приписана функция, определяющая интенсивность соответствующего процесса во времени. Так как присутствует большое количество нулевых функций (что означает отсутствие процесса преобразования из одной вершины в другую), то удобно указать список этих функций с помощью матрицы сопряженности

	j = 1	j = 2	j = 3	j = 4	j = 5	j = 6	j = 7	j = 8
i = 1	a i ( t )	a 12 ( t )	a 13 ( t )	a 14 ( t )	0	0	0	a 18 ( t )
i = 2	0	a 2 ( t )	0	0	a 25 ( t )	0	a 27 ( t )	0
i = 3	0	0	a 3 ( t )	0	0	a 36 ( t )	0	0
i = 4 M ( t ) =	0	0	0	a 4 ( t )	0	0	a 47 ( t )	0
i = 5	0	0	0	0	a 5 ( t )	0	0	0
i = 6	0	0	0	0	0	a 6 ( t )	a 67 ( t )	0
i = 7	0	0	0	0	0	0	a 7 ( t )	0
i = 8	0	0	0	0	0	0	a 87 ( t )	a 8 ( t )

Элемент матрицы M ( t ) в i -й строке и j -м столбце есть интенсивность реализации соответствующего преобразования и коэффициент в модели, описываемой уравнениями (1). Нули в матрице определяют равенство нулю соответствующего слагаемого в модели.

Опишем теоретические подходы к заданию ненулевых элементов матрицы сопряженности. Коэффициент a p ( t ) соответствует интенсивности пролиферации мезенхимальных стволовых клеток. Будем считать, что интенсивность пролиферации мезенхимальных стволовых клеток постоянна, поэтому имеет смысл принять этот коэффициент равным константе K , значение которой можно определить лабораторным путем.

Элемент    ad* (t)    соответствует интенсивности дифференциации мезенхимальных стволовых клеток в фибробласты. Процесс этой дифференциации плохо изучен, но можно предположить, что поскольку фибробласты активно участвуют в ремоделировании костной ткани путем синтеза компонентов межклеточного вещества, то этот процесс должен активизироваться еще на стадии воспаления. Поэтому полагаем

a * ( t ) = А₁₂ Ф , ( t ) + S „ ( t ) ,                                (8)

где A_n - масштабный коэффициент; S ,₂ ( t ) - функция, отвечающая за механическую стимуляцию процесса.

Отметим, что A подбирается из сравнения теоретического прогнозирования с реальными данными для более точного описания процесса. Величина S ,₂ ( t ) может рассматриваться как управляющая переменная, в частности отвечающая за механическую стимуляцию процесса. Здесь и далее подобные переменные предполагаются кусочно-постоянными на временном отрезке функциями.

Коэффициент a df ( t ) соответствует дифференциации мезенхимальных стволовых клеток в хондроциты. Известно, что мезенхимальные стволовые клетки соединяются в хондрогенные островки, клетки которых размножаются и дифференцируются в хондробласты. Хондробласты затем дифференцируются в хондроциты. Существенно на процесс влияют факторы TGF-β S и IGF-1. Поэтому полагаем

a * ( t ) = 4з ( в 1з Ф 1 ( t ) + Р Г3 Ф 2 ( t ) ) + S 13 ( t ) ,                         (9)

где A ₃, Р1₃, Р2₃ - масштабные коэффициенты; S ,₃ ( t ) - функция, отвечающая за механическую стимуляцию процесса.

Коэффициент a d* ( t ) отвечает за процесс дифференциации мезенхимальных стволовых клеток в остеобласты. В ходе прямого остеогенеза мезенхимальные стволовые клетки при образовании остеогенных островков непосредственно дифференцируются в остеобласты. Активное влияние на эти процессы оказывают все рассматриваемые нами факторы: TNF-α, IGF-1, TGF-β S , BMP-5, BMP-6, VEGF, BMP-2. Поэтому удобным представляется следующее выражение коэффициента:

a * ( t ) = А з ( P^ 1 ( t ) + e ?4 ® 2 ( t ) + Р З4 Ф 3 ( t ) ) + S 14 ( t ) ,                (10)

где A_M, P1₄, P2₄, 334 - масштабные коэффициенты; S ₁₄ ( t ) - функция, отвечающая за механическую стимуляцию процесса.

Аналогично получим выражения коэффициентов, моделирующих действие фибробластов по созданию межклеточного вещества для организации костной ткани:

a  ( t ) = А 22 Ф 1 ( t ) , a d* ( t ) = А 25 Ф 2 ( t ) , a 2* ( t ) = А 27 Ф 2 ( t ) .              (11)

Коэффициенты, описывающие интерстициальный рост хряща, можно задать следующим образом:

a " ( t ) = А 33 Ф 2 ( t ) , a* ( t ) = А з₆ Ф 2 ( t ) .                       (12)

С другой стороны, аппозиционный рост хряща можно задать с помощью следующего выражения:

aP (t ) = '■' Ф (t).(13)

Образование остеобластов и дальнейший остеогенез опишем, используя соотношения aP (t ) = A4 ^2 (t) + в 241- (t)), adf (t ) = А^Ф. (t),(14)

а учитывая существенное влияние факторов TGF-β S , BMP-5, BMP-6, IGF-1 на развитие соединительных тканей, получим

< (t ) = А55Ф2 (t).(15)

Результат непрямого остеогенеза предлагается описать следующим образом:

adf (t ) = Аб7Фз (t).(16)

Функциональный коэффициент, который определяет активность таких биологических процессов, как минерализация костной мозоли, образование первичного губчатого вещества (ретикулофиброзной ткани), формирование надкостницы и наращивание остеоцитов посредством разрушения ретикулофиброзной костной ткани (создание пластинчатой ткани), зададим в виде aP (t ) = А Ф (t)-A^ (t),                      (17)

где A ^некр – подбираемый коэффициент, определяющий интенсивность разрушения костной ткани при некрозе на стадии воспаления.

Для последних коэффициентов матрицы сопряженности, характеризующих образование сети кровеносных сосудов, примем следующие функциональные зависимости:

a " ( t ) = А Ф. ( t ) , <  ( t ) = А Ф .4 ( t ) .                        (18)

Наконец будем предполагать, что интенсивность апоптоза существенно не зависит от процессов регенерации, а следовательно, можно установить для всех типов клеток и тканей простые выражения aa (t ) = P,                                   (19)

где P – константы.

План численного решения основной краевой задачи

Для значений i = 1...4 уравнения (1) относительно неизвестных функций c , i = 1...4 являются дифференциальными уравнениями в частных производных второго порядка вида «реакция–диффузия», которые нередко возникают в химической кинетике. Система (1) первых четырех уравнений ( i = 1...4 ) в случае известных функций Cj ( j = 5...8 ) при граничных условиях (2) и начальных условиях (3) может быть численно решена методом прямых, или методом Роте [2]. При i = 5...8 в системе (1), как было отмечено выше, коэффициенты D и k должны быть равными нулю, что приводит к дифференциальным уравнениям в частных производных первого порядка.

Тогда система (1) последних четырех уравнений ( i = 5...8 ) в случае известных функций Cj, j = 1...4 при начальных условиях (3) может быть численно решена относительно неизвестных функций c , i = 5...8 тем или иным сеточным методом [4].

Отсюда естественным образом возникает следующий план численного решения дифференциальной краевой задачи (1)–(3) с восьмью неизвестными функциями c , i = 1...8 (конкретизацию, обоснование и численную реализацию этого плана предполагается изложить в последующих работах авторов). Согласно (3) нам известны значения всех восьми неизвестных функций ct, i = 1...8 при t = 0 и всех x из [0, l]. Поэтому, применяя явную разностную схему (с шагом τ по переменной t и с шагом h по переменной x, где h = — и m - натуральное число) к системе последних четырех уравнений (1), находим приближенные значения функций c , i = 5...8 при t = т и всех x = kh, где к = 0...m. Используя интерполяцию функций, получаем приближенные аналитические выражения для функций c , i = 5...8 при t = т и всех x из [0, l]. Зная эти аналитические выражения и применяя метод Роте [2] к первым четырем уравнениям (1), с учетом (2) и (3) находим приближенные аналитические выражения для функций c, i = 1...4 при t = т и всех x из [0, l]. Теперь нам известны приближенные аналитические выражения для всех восьми неизвестных функций c , i = 1...8 при t = т и всех x из [0, l]. Это позволяет нам, повторяя описанный только что вычислительный процесс с заменой t = 0 на t = т, получить приближенные аналитические выражения для функций c , i = 1...8 при t = 2т и всех x из [0, l], затем на их основе аналогично - при t = 3т, потом последовательно при t = 4т, t = 5т и т.д.

Предложенная в настоящей статье математическая модель описывает основные биологические процессы, происходящие при восстановлении или перестройке костной ткани. Полученные данные, с учетом использования в модели факторов роста, позволят смоделировать ряд патологических процессов, происходящих в костях при врожденных, эндокринных и других системных заболеваниях. Это позволяет применять ее не только в научных целях при описании патогенеза заболеваний, но и при моделировании состояния кости при использовании фармакологических средств и изделий медицинского назначения. Таким образом, после всесторонней верификации применение предложенной модели будет актуальным не только в травматологии и ортопедии, но и в эндокринологии, ревматологии, терапии, онкологии, фармакологии.

Заключение

В статье представлена одномерная модель процесса восстановления кости в условиях механической и биохимической стимуляции. В нее заложено большое количество исследуемых в работе разнообразных связей и зависимостей между основными типами клеток и тканей, составляющих кость и влияющих на процесс ее восстановления. Рассматриваются также вопросы, связанные с численной реализацией модели.

Ее реализация и применение требуют проведения тестовых вычислительных и натурных экспериментов, что выходит за рамки настоящей статьи. Представленные результаты служат основой для дальнейших теоретических исследований в достаточно новой интенсивно развивающейся области на стыке вычислительной биомеханики и тканевой инженерии, посвященной теоретическому изучению влияния биохимического и механического воздействия на биологические процессы ремоделирования и репаративной регенерации ткани после переломов, эндопротезирования, применения перспективных пористых имплантатов.

Благодарности

Работа выполнена при поддержке гранта Российского фонда фундаментальных исследований № 15-29-04825.