Математическая модель конкуренции популяций на загрязненной территории

Бюллетень науки и практики / Bulletin of Science and Practice

УДК 51(075.8)                                      

Техногенные вмешательства в природную среду стали соперничать со многими природными процессами, оказывая мощное воздействие на природные комплексы, вызывая нарушения нормального хода протекающих в различных биогеоценозах процессов. Вредные для всего живого вещества антропогенного происхождения наполняют воздушный и водный бассейны, загрязняя обширные территории [1, 2], Загрязнение среды обитания ведет к кардинальным изменениям условий существования населяющих эти территории растений и животных, может изменить направленность и формы естественного отбора [3], способно изменять генетическую структуру природных популяций [4], привести к уменьшению видового разнообразия и исчезновению отдельных видов [5]. В дополнение к этому изменяется и интенсивность межвидовых взаимоотношений, обусловленная различной реакцией особей на внешние воздействия. У конкурирующих популяций изменяется численность, происходит смена доминирующих видов, некоторые виды исчезают [6].

Проникновение химических веществ в организмы человека, птиц, млекопитающих и рыб происходит через органы дыхания, желудочно-кишечный тракт, кожные покровы и слизистые оболочки. В растения загрязняющие вещества попадают при корневом питании, путем газообмена и обменной адсорбции с поверхности листовой пластинки. По мере поступления в трофические цепи токсиканты аккумулируются в их конечных звеньях, оказывая негативное влияние на клеточном, гистологическом, организменном и популяционном уровнях. Уровень накопленных токсикантов в организме зависит от возраста, пола, путей поступления в организм [4]. Накопление токсикантов сопровождается изменением плодовитости и смертности характерными для каждого вида.

Математическая модель

Для описания динамики численности двух конкурирующих популяций используется локальная «модифицированная» математическая модель Вольтерры [7], учитывающая как межвидовую, так и внутривидовую конкуренцию:

du

— = A u 1 ( 1 - u 1 - Y 1 u 2 ) ,

“~2“ = ^2U1 (1 - u2 - YЩ ) , где u и u2 — численность популяций, ^ и ц2 — удельные локальные скорости роста численности популяций, y и Y — параметры, характеризующие интенсивность конкуренции. Емкости сред обеих популяций приняты в модели (1) равными единице [7].

Система уравнений (1) имеет четыре неподвижные точки

• 1.    щ = 0, u ₂ = 0.

• 2.    u = 1, u ₂ = 0.

• 3.    u = 0, u ₂ = 1.

• 4.    ^u 1 = ( 1 ^- Y ) / ( 1 ^- / 1 / 2 ) , ^u 2 = ( 1 ^- Y 2 ) / ( 1 ^- Y 1 Y 2 ) ,

если y >  1 и y >  1, или Y <  1 и.

Первая точка является неустойчивой, вторая будет устойчивой, если y <  1 и Y >  1, а третья, если Y >  1 и у ₂<  1. Четвертая стационарная точка реализуется и будет устойчивой, если одновременно выполняются неравенства y <  1 и у ₂<  1. То есть, если внутривидовая конкуренция у популяций слабее межвидовой ( у₂ <1 и y <1), то совместное существование популяций будет устойчивым [7].

Тяжелые металлы, выбрасываемые предприятиями в окружающую среду, образуют токсичные для живых организмов вещества. Токсиканты постукают в организмы либо непосредственно, либо по трофическим цепям. Накопление их в организме со временем приводит к внутренним изменениям. В модели предполагается, что изменения метаболизма вызывают понижение плодовитости особей [3]. Предполагается также, что рождаемость особей с увеличением количества токсикантов P уменьшается по гиперболической зависимости

R (P) =

1 + ap

1 + a2P,

где a^ и a₂ — положительные параметры такие, что a j <  a ₂.

Часть среды обитания при антропогеном давлении может стать недоступной для особей популяции, или часть трофического ресурса может быть уничтожена. Этот фактор в модели учитывается через уменьшение емкости экологической ниши популяции. Уменьшение емкости ниши K происходит по гиперболической зависимости:

K (P) =

1 + bP

1 + b2P

где b и b₂ — положительные параметры такие, что b <  b ₂.

С учетом этих предположений модель конкуренции двух популяции (1) в загрязненной зоне сводится к задаче Коши для системы двух дифференциальных уравнений

du	' 1 + aP  1 + bP      b
—1 = m	1    11        /‘ тР  Y1 и 2	,
dt         \	1 + a^p  1 + byp
du	( 1 + a?p  1 + bp	b
= ^ u 2	---—---—— и - Y U ^ 1 + a2p 1 + b22P 2   2

где a:i и b ( i, j = 1,2) - параметры, удовлетворяющие неравенствам ij          ij a11 — a12

a 21 ^— a 22 , ^b12 ^{— b} 11^{, b}22 ^{— b}21 •

На параметры Y и Y накладываются ограничения: 0 — Y 1 <  1 , 0 — Y <  1 , тем самым предполагается, что в отсутствие токсикантов ни одна из популяций не гибнет.

При P = 0 (токсиканты отсутствуют) эта модель переходит в модель (1). Удельная скорость роста популяций в зависимости от значения P при выполнении условий (3) уменьшается, но не может уменьшиться более чем на величину ^a_{ j / a₁₂ для первой популяции, и на величину ^₂a ₂j / a₂₂ для второй популяции. Этим учитывается факт ограниченного накопления токсикантов организмами особей популяций и неоднородность накопления внутри самих популяций [3, 4].

Загрязнители среды могут уничтожить часть трофического ресурса или сделать его недоступным для особей популяций. Емкости ниш популяций при выполнении неравенств ^b 11 >  ^b 12 и b ₂j >  b₂₂ в (2) с увеличением количества загрязнителей будут уменьшаться. Предполагается, что емкость ниши первой популяции не может стать меньше величины b 1 / b 2, а второй — b ₂j / Ъ₂₂ . Этим учитывается то обстоятельство, что небольшая часть популяций может выдержать антропогенную нагрузку.

Нетривиальная неподвижная точка системы уравнений (2) определяется через параметры модели:

и =

j_ ( i + bp i + ap D ^ 1 + b₂₂P 1 + a_nP

- Y 1

i + aP^л 1 + a 22 P J

1 (1 + bP 1 + a2,P    1 + aP У u7 = — ---—--21--Y----11—

• ² D ^ 1 + b_nP 1 + a₂₂P    1 + a_nP J

  где

  
  

  D =

  
  

1 + bP 1 + b₂₁P

1 + b_nP 1 + b₂₂P

Поскольку при P = 0 эта стационарная точка существует и является устойчивой (поскольку y <1 и Y i <1), то в силу непрерывности правых частей выражений (4) от P , она будет существовать и при малых значениях P .

Собственные значения матрицы Якоби

J =

- ш ---¹¹ и

1 1 + b₁₂P ¹

-Y1PU1

^-Y 2 ^ 2 ^U 2

- ш ----²¹ u₂

2 1 + b₂₂P ²

системы уравнений (2) в стационарной точке (4) будут иметь отрицательные вещественные части, если выполняется неравенство

D =

1 + bP 1 + b_2iP

^- Y 1 Y 2 >  ⁰.

1 + b₁₂P 1 + b₂₂P

Поскольку рассматривается модель, для которой выполняются условия (3), то, соответственно неравенство D >  0 при 0 <  y <  1 и 0 <  Y2 <  1 будет выполняться. То есть, если стационарная точка (4) реализуется, то она будет устойчивой.

Распределение вероятностей

Реализация математических моделей популяционной биологии возможна во встроенном модуле SIMBIOLOGY среды программировании математического пакета Matlab [8]. Имитационная модель основывается на случайном переборе параметров модели (2) из заданного диапазона значений [9] с учетом соотношений (3). При заданном количестве вариантов выбора параметров строятся вероятности распределения отклонений стационарных значений численностей популяций при антропогенном давлении от естественных значений.

На Рисунке 1 приведены распределения стационарных значений численностей популяций при Y2 = 0.6, Yi = 0-1 и P = 1.5 для параметров выбранных случайным образом из диапазонов an е (1,2) , a2j g (1,2) , a12 g an + (0,1) , a12 е an + (0,1) , b22 e (0,1) , bn g (0,1) , bn e b12 + (0,1) , b21 e b22 + (0,1) . На Рисунке 2 приведено вероятностное распределение численности популяций для 2 000 вариантов выбора параметров системы уравнений (2). Такой вариант выбора параметров обеспечивал выполнение неравенств (3). Пунктирными линиями на Рисунке 1 и Рисунке 2 отмечены стационарные значения численностей популяций для чистой территории. Сплошной линией на Рисунке 1 отмечена граница области, в которой лежат стационарные значения численности популяци0439.

В рассмотренном варианте параметров большие потери несет та популяция, которая в отсутствие токсикантов имеет большую численность (на Рисунке 2 — u ). Знание реальных параметров, входящих в модель (2), дает возможность прогнозировать степень влияния антропогенной нагрузки на численность популяций для реальных экосистем [10, 11].

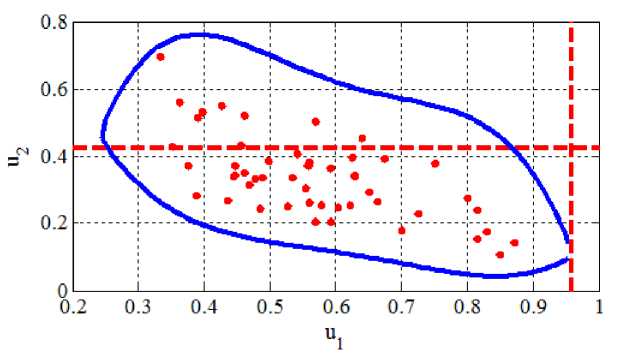
Рисунок 1. Распределения стационарных значений численностей популяций

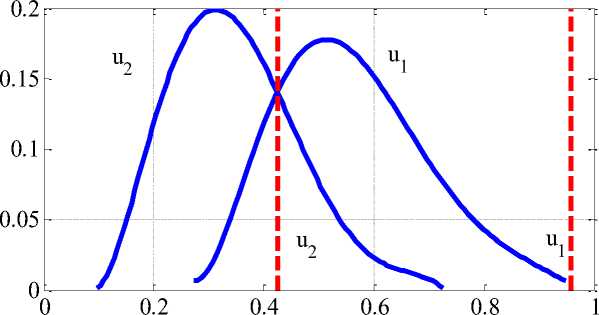
u1, u2

Рисунок 2. Распределение вероятностей численности популяций при антропогенном давлении

Заключение

Таким образом, разработанная модель прогнозирует сдвиг распределений вероятностей в сторону уменьшения численности обеих популяций при наличии токсикантов, по сравнению с их численностью в «чистой» среде. Наибольшие потери численности будут у популяций, которые до антропогенного давления имели большую численность. Численность малочисленных популяций может вырасти за счет уменьшения давления конкурирующих популяций.