Математическая модель напряженно-деформированного состояния цилиндрической оболочки с осевым трехмерным дефектом
Автор: Остсемин А.А., Уткин П.Б.
Статья в выпуске: 27 (127), 2008 года.
Бесплатный доступ
Рассматривается математическая модель о разрушающем кольцевом напряжении для тонкостенных труб с осевым поверхностным эллиптическим дефектом. Используя метод Колосова-Мусхелишвили, было найдено аналитическое решение при некоторых предположениях на граничные условия. Критериями разрушения выбраны два условия. Первое связано с критическим значением раскрытия трещины, второе - с достижением напряжения в нетто-сечении трещины напряжения разрушения для данного материала. В частном случае формулы превращаются в формулы, ранее полученные аналогичным образом, для трубопроводов с линейной трещиной.
Механика разрушения, метод колосова-мусхелишвили, тонкостенная оболочка, осевой поверхностный эллиптический дефект
Короткий адрес: https://sciup.org/147159057
IDR: 147159057 | УДК: 539.4
Mathematical model of the stress-strain behaviour of central three-dimensional defect
The authors consider a mathematical model concerning breaking hoop stress for thin-walled pipes with the central elliptical part-through crack. On the basis of a certain theoretical analysis by Kolosov-Muskhelishvili's method the analytical solution is obtained. Two rapture criteria are used. The first criterion is based on critical displacement of crack borders. The second criterion considered the stress existing in the ligament near the moment of rapture, which is considered to be equal to material yield stress. Obtained formulas are generalizing previously existing formulas for linear crack.
Текст научной статьи Математическая модель напряженно-деформированного состояния цилиндрической оболочки с осевым трехмерным дефектом
Магистральные газонефтепроводы представляют собой сложные технические системы, разрушение которых приводит к опасным экологическим и большим экономическим последствиям. По протяженности свыше 30% трубопроводов Западной Сибири эксплуатируются более 20 лет, 18% - более 30 лет. Средний возраст трубопроводов составляет 25 лет. Количество магистральных трубопроводов, достигших критического срока эксплуатации, является достаточно большим. В связи с этим возникает актуальная задача проведения своевременной диагностики. Трубы отечественного производства уступают японским по многим показателям. Относительное удлинение 5 разрушившихся отечественных труб ниже на 7 - 45% и характеризует резкое снижение пластичности. Сравнительная статистика на газонефтепроводах по данным, имеющимся в Ростехнадзоре, показывает, что наибольшее число аварий происходит на магистральных газопроводах. Основная причина их разрушения - это коррозионные повреждения стенок трубопроводов. Эта часть аварий возрастает со временем. Существуют несколько видов коррозии: общая, локальная (питтинговая, канавочная) и стресс-коррозия. Многолетний опыт эксплуатации газонефтепроводов показывает, что существенная доля их повреждений связана с возникновением коррозионных язв, питтингов и микротрещин, дальнейшее развитие которых приводит к разрушению.
Результаты исследования аварий на трубопроводах показали, что нормы (СНиПы, 205.06-85, Ш-42-80) технического проектирования устарели, не обеспечивают нужной безопасности, не отражают прогресса науки и техники в трубопроводном транспорте. Поэтому эти документы должны быть переработаны. Актуальной является разработка методик, нормативно-технических документов и программных продуктов, обеспечивающих научно обоснованные нормы дефектов в основном металле и сварном шве, прогнозирование сроков эксплуатации магистральных газонефтепроводов и резервуаров [1].
Очаг разрушения представляет собой рваную ломаную поверхность, которая образуется в процессе объединения (слияния) мелких (по длине), но разных по глубине, поверхностных трещин. Поэтому трещиноподобный дефект представляет половину эллипса [2, 3]. Повреждение поверхности металла характеризуется зарождением на локальном участке множества коррозионно-механических трещин вблизи заводского продольного шва по зоне термического влияния или по зоне загиба кромок штрипса.
Опыт исследования разрушения труб из отечественных и зарубежных сталей показывает, что очаг разрушения формируется в основном из мелких трещин длиной до 35 мм. Первоначальные трещины распространяются на глубину до 50% от толщины стенки трубы. Критическая длина поверхностных трещин составляет 140-150 мм.
Большое количество коррозионно-механических дефектов и разрушений труб магистральных газонефтепроводов указывает на необходимость детального исследования разрушения и целесообразность тщательного исследования трехмерной математической модели труб с полуэллиптическим дефектом для предупреждения аварийных отказов во время эксплуатации и нормирования дефектов при диагностике магистральных трубопроводов.
Математическая модель поверхностного дефекта
Для труб большого диаметра кривизной поверхности можно пренебречь и рассматривать вместо цилиндрической оболочки пластину с поверхностным эллиптическим дефектом.
Рассмотрим пластину с поверхностным эллиптическим дефектом. На рисунке показана половина дефекта. Мы предполагаем, что длина нетто-сечения равна действительной длине трещины 2/, тогда как длина трещины, включая зоны пластичности у концов трещины, равны 2а. Эти два параметра связаны соотношением
I = acos(a).
Напряжение на бесконечности равно од, функция распределения напряжения около вершины А и симметричной ей вершины поверхностного дефекта, которая зависит от расстояния ж до центра дефекта, предела текучести ат, предела прочности а в, напряжения пластического течения а = куав считаем равной:
Р(ж) = (£ — d) I а — (ст —
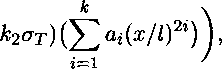
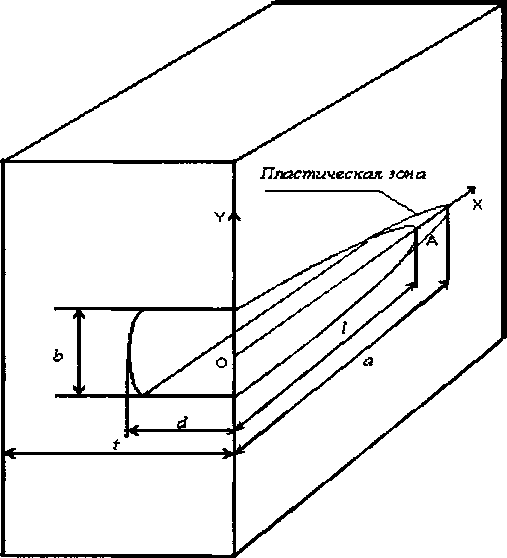
Схематическое изображение дефекта где ку характеризует момент потери устойчивости (напряжение пластического течения ст) пластического деформирования участка около вершины дефекта, учитывает коэффициент двухосности нагружения стенки трубы то и показатель деформационного упрочнения п степенной аппроксимации диаграммы деформирования; кз определяет границу локализованной пластической зоны и зависит от коэффициента поперечной деформации ц. Исходя из условий задачи, предполагаем симметричность функции напряжений (1), которая аппроксимируется полиномом четной степени. Предполагается также, что эти силы распределены независимо от глубины листа. Соответствующее распределение напряжения, которое будет использовано как граничные условия соответствующей плоской задачи упругости, равно ст(ж) = P(x)/(t — d). Также предполагаем, что напряжение на к концах трещины равно к2ат, что означает равенство ^«j = 1.
Используя метод Мусхелишвили Н.И. [4], разбиваем задачу на три подзадачи, первая из которых состоит в вычислении комплексных потенциалов для ненапряженного состояния в окрестности трещины (напряжение на границе трещины равно 0 и напряжение на бесконечности равно сту), вторая задача учитывает напряжение, передаваемое через связку, и последняя задача учитывает напряжение в вершине дефекта (в пластической зоне). В завершении для суммирования этих задач предполагаем, что результирующий комплексный потенциал может быть получен как сумма решений выше перечисленных задач с определенными весами, а именно, мерой зоны действия соответствующих сил (принцип суперпозиции).
Комплексные потенциалы <ру и фу для дефекта, с половиной длины в 1 единицу были вычислены в [5]:
<^1(0 =
ее
4(1 + т)
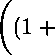
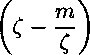
2(1-е) \
^ = 2^5
[(1 — е) + (1 + б)т] (1 + т2)
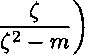
где т =---- (а, Ъ - большая и малая полуоси эллипса) - параметр эллипса, е - параметр о + о двухосности нагружения оболочки.
Комплексные потенциалы ip^ и ^>з, которым соответствует замена сил в вершинах дефекта приняты, согласно [4], как частный случай решения задачи о плоскости с полуэллиптическим отверстием, подвергнутым постоянной нагрузке на своей части:
2таат
ат .
-—: zln 2тгг
2 _ е2га \ / 1 _ £2 _|_ 2г£ sm(ai)
;-----— cos (a) In ------- ™ . ..........г
- — е-2га / \ 1 — £2 — 2г£ sin(a)
. 1 — m г 1 + m
sin(a) In
1 + £2 — 2£ cos(o-)\
1 + £2 — 2£ cos(a) /
2(1 + т^аат С от Г , .. /1 - <2 + 2г( sin(a) \ ^3 =---7ГТ—>— 72----+ Т- cos (а) 1п( -^— . , , ) + тг( 1 + т) £2 — т 2тгг \ 1 — £2 — 2г( sm(a) /
. 1 — т
+? 1 + т
sin(o) In
1 + £2 — 2£ cos (а) \
1 + С2 + 2( cos(o) /
Комплексные потенциалы у?2 и ^2> отвечающие растягивающей силе (1) и полудлине дефекта, равного единице, могут быть вычислены с использованием комплексных потенциалов у?з и ^з по формулам:
тг/2
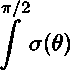
а№ = Р(1С«#)
V2
= / ^(0) —,
J от
Подставляя в (6) формулы (1), (4) и (5) получаем формулы для комплексных потенциалов 992 и ^2: Ч>2 = (куав - (кгав - ^стт) ^ ^) (f^)^
(кутв - к2ат)
2(m
+ 1)
(
2^2i—2Z+1
2г - 2Z + 1
2т^2г 2,-1
2г-21-1
1 । ^2 / к * = тт^- UvTB-^B-kOT^-y^ ЬгЦ^+т с8) X I »'и \ , V lib где G(^ не имеет особенности в фокусах эллипса (С = ±i/m). Для линейного случая m = 1 и формулы (2)-(8) совпадают с аналогичными формулами из [6]. Комплексные функции для задачи будем вычислять как сумму трех пар вышеперечисленных потенциалов, взятых с определенными весами. В качестве весов возьмем меры областей действия сил, описанных в каждой из этих задач.
Ф =
Ja
, Л т d\ d cos(o) \ Ф = Л cos(a) j ^1 + Ja cos(a) fl - ^ j ^2 + ^ V’s- Здесь Ja есть четверть длины эллипса с параметром т и большой полуосью а; 1 \ 2 1 — т\ 2j ——■ cos a; dx. 1 + т/ Точный подсчет данного значения невозможен, поэтому оно вычисляется численными методами приближенно. Подставляя в (9) приведенные выше функции (2)-(5), (7), (8) и преобразовывая результат, получаем: Ja cos (a) С 2(1+ m) oq (2(1 — e) + m(l + e)) 4(m + 1) 2таат d 7Г t Ja cos (a) / _ tA к^ов - k2aT A у _ 2m£2j 21 A _ (ю) + m + 1 V t) 2 22i 2i \ 2г - 2Z + 1 2г - 21 - 1 J x ' i=l z=o 4 ' аат d г / £2 — e2 X / м /1 — С2 + 2г£ sm(a) X •—- - — In I ----— -cos(a)ln -—; ( 1 2ттг t [a \£2 — е-2ю/ \1 — С2 — 2г£ sin(a) / . 1 — m Z 1 + m sin(ct) In 1 + C2 — 2^ cos(a) X 1 + C2 + 2^ cos(a) / Ф = 2JaC cos(a) 1 + m2 к C2 — m [ 2 1+m yx OiL^ / 22г г=1 O'S (1 + m2)(l — e + (1 + s)m) (d 2m(m + 1) X V dX / xX a(l + m2)^ d - cos (a) + -— ----r— -t J v J tt(1 + m) t a a J (И) aCTT / м —— - cos(a) In 2ттг t v v 1 — ^2 + 2i( sin(a) X 1 — £2 — 2г^ sin(a) / + г 1 — m 1 + m • м /1 + <2 - 2( cos(a) sm(a)ln ——-—t-г v 7 \ 1 + £2 + 2£ cos(a) +Ja COs(ct) (1 - ^ G«). Для нахождения размера пластической зоны (определения параметра а) воспользуемся тем же приемом, что и Дагдейл [7]. Считаем, что у комплексного потенциала Ф по формуле (11) нет особенностей в фокусах эллипса (коэффициент при выражении -=---- — т равен нулю). cos (о) М - Мчав - Очав - к^о^ ^ -^г —Од cos (а) (1 — е) + (1 + ё^т d (1 — е) + (1 + Е)т 2m °® t 2т ct d аат it t Ja Преобразовывая уравнение (12), получаем: ад (1 - е) + (1 + e)m\ . . --z----------1 cos (а от 2т / ' 2а d а _ ад d (1 — е) + (1 + е)т к t ]й ат t 2т Из уравнения (13) можно найти параметр а и, как следствие, размер пластических зон по формуле а — I = а(1 — cos(a)). Далее через функцию Ф (10) можно определить перемещение трещины в центре, которое мы приравняем критическому раскрытию 5С 4 „ §с v = --Ке(гФ) = —. . 7Г После вычисления Ке(гФ) в точке 9 = — получаем из (14) следующее уравнение для раскрытия трещины: 5с = 41ад Г Ja --^ •пЕ а 2d t d 1 — m t 1 + m sin(2ci!) к + k2 CliAi i=l 1 — m m(l — e) „ . .d 1 — m m(l — s) x------;---z;----r™ — 2ojcos(ai)— -----—----;---7-----r— 1+m (1 — e) + (1 + s)m t 1 + m (1 — е) + (1+е)ш ГДеЛ 22i §^( 1)* '(2^-2/ + ! +2i-2l-l)' Величина 5C есть характеристика материала [2]. Таким образом, формулы (13) и (15) устанавливают связь между геометрическими характеристиками дефекта, характеристиками материала и кольцевым разрушающим напряжением на бесконечности ад. Из формулы (15) можно определить параметр а численными методами, решив данное трансцендентное уравнение. Далее, воспользовавшись (13), определим кольцевое напряжение ад: _ 2тстт °в (1 - е) + (1 + б)т Х Используя формулы (13) и (16), можно вычислить разрушающее напряжение для пластины с поверхностных эллиптическим дефектом. При m = 1 формулы (13) и (16) превращаются в соотношения для трубопровода с трещиной работы [6]. Выводы 1. На основе метода Колосова-Мусхелишвили создана математическая модель определения напряженного состояния цилиндрической оболочки с осевым эллиптическим поверхностным дефектом, получены новые формулы для комплексных потенциалов и тензора напряжений. 2. Проведен теоретический анализ по определению разрушающего кольцевого напряжения при вязком разрушении труб, сосудов давления с продольным полуэллиптическим дефектом с использованием методов упруго-пластической механики разрушения и критерия разрушения в виде критического раскрытия дефекта.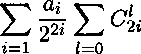
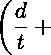
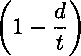
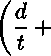
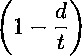
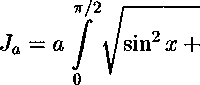
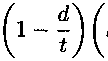
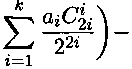
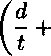
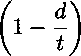
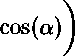
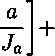
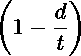
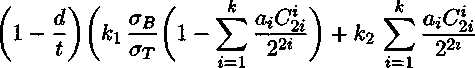
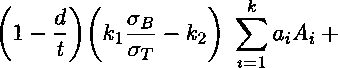
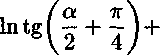
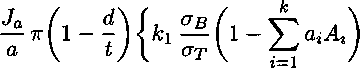
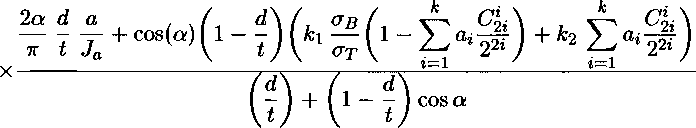
Список литературы Математическая модель напряженно-деформированного состояния цилиндрической оболочки с осевым трехмерным дефектом
- Остсемин А.А. Анализ несущей способности действующего магистрального нефтепровода при наличии дефектов в продольном сварном шве/А.А. Остсемин//Сварочное производство. 1998. № 9. С. 11-15.
- Красовский А.Я. Трещиностойкость сталей магистральных трубопроводов/А.Я. Красовский, В.Н. Красико. Киев: Наук. Думка, 1990. 176 с.
- Орыняк И.В. Расчет давления вязкого разрушения трубы с осевой сквозной трещиной/И.В. Орыняк//Проблемы прочности. 1993. № 4. С. 39-48.
- Мусхелишвили Н.И. Некоторые основные задачи математической теории упругости/Н.И. Мусхелишвили. М.: Наука, 1966. 708 с.
- Остсемин А.А. К вопросу о предельном равновесии пластин с трещиноподобными дефектами/А.А. Остсемин, П.Б. Уткин//Известия Челябинского научного центра. 2006. № 4(34). С. 1-6.
- Остсемин А.А. Упруго-пластическое разрушение труб с поверхностной трещиной/А.А. Остсемин, П.Б. Уткин//Вестн. ЮУрГУ. Серия "Математика, физика, химия". 2006. Вып. 7, № 7(84). С. 130-136.
- Dugdale D.S. Yielding of steel sheets containing splits/D.S. Dugdale//J. Mech. Phys. Solids. 1960. Vol. 8. P. 100-104.


