Математическая модель напряженно деформированного состояния двухслойного упругого сферического тела с учетом пористой структуры материала

В настоящее время актуальными остаются вопросы строительства и охраны подземных сооружений различного назначения, в том числе подземных сферических полостей. При этом возникает необходимость решения ряда сопутствующих задач, таких, как борьба с горными ударами, взрывные подземные работы, охрана окружающей среды от загрязнения, проблемы сейсмобезопасности и др.

Цель расчета подземных конструкций заключается в определении полей напряжений и перемещений, возникающих в элементах этих сооружений и установлении условий их прочности и устойчивости. В соответствии с результатами расчета выбираются рациональные конструкции крепей и оптимальные размеры их сечений, обеспечивающих надежную работу сооружений при минимальных затратах.

Обеспечение устойчивости неглубоких выработок при достаточно прочных вмещающих породах, как правило, не составляет особых затруднений. Однако в настоящее время непрерывно увеличивается объем горных выработок, проходимых на больших глубинах и в сложных горногеологических условиях (многолетняя мерзлота, высокая сейсмичность, неотектонические явления и т.п.), что отчасти связано с активным освоением арктического пространства. При нарушении условия благоприятного сочетания глубины и прочности материалов, обеспечение устойчивости выработок и их крепей приобретает черты сложной инженерной и научной проблемы.

Для решения всех этих вопросов необходимы представления о разрушении горных массивов, а также об устойчивости крепей подземных сооружений.

Разрушение крепи подземной конструкции может произойти в результате следующих двух ситуаций: 1) достижение напряженно-деформированным состоянием (далее НДС) пределов прочности; 2) достижение напряженно-деформированным состоянием критических значений, соответствующих потере устойчивости (отказу) крепи.

Решение первой задачи основано на сравнении найденного (в аналитическом или численном виде) НДС с пределами прочности материалов. Во втором случае начальным этапом решения задачи устойчивости является нахождение в аналитическом виде основного НДС конструкции. В связи с этим получение аналитических соотношений, описывающих докритическое НДС в аналитической форме, является актуальной задачей.

Механика

Помимо объектов исследования механики горных пород слоистые сферические конструкции находят широкое применение в различных областях строительной механики и машиностроения. Поэтому вопрос определения и анализа НДС с учетом различных физико-механических и геометрических параметров сферических конструкций является объектом внимания достаточно большого количества исследований. Так в монографии [1] в рамках теории малых деформаций в аналитическом виде получены поля напряжений и перемещений горного массива вблизи сферической полости при учете неупругой работы грунта. В работе [2] найдено НДС монолитной сферической крепи подземного нефтехранилища с учетом начальной пористости материала и сложной реологии сжатой матрицы. В статье [3] на основе метода малого параметра получены приближенные аналитические выражения НДС упругого пространства, ослабленного сферической полостью, с учетом температуры.

В настоящей работе решается задача определения НДС двухслойного сферического тела, находящегося под действием сжимающих нагрузок интенсивностями q_b и q_a , равномерно распределенных по внешнему и внутреннему контурам тела соответственно. Материал внешнего слоя будем моделировать упругим сжимаемым телом с параметрами Ламе 2 1 , ц . Деформирование материала внутреннего слоя, имеющего пористую структуру, разделим на два этапа [4, 5]. Первый этап – деформирование среды при наличии несжатых пор, второй – деформирование сжатого скелета. На первом этапе в качестве модели материала принимается модель упругого сжимаемого тела с параметрами Ламе 2 2 , ц ₂ , на втором - модель упругой несжи-

Рис. 1. Двухслойное сферическое тело при сжатии

маемой среды с модулем сдвига ц = ц2 + ц3. Согласно работе [6], в качестве условия полного сжатия пор в некоторой точке среды выбирается условие равенства объемной деформации в этой точке величине £0 - начального раствора пор.

Обозначим радиус внешней границы b , внутренней границы a , радиус недеформированной границы контакта слоев – с (рис. 1).

На первом этапе деформирования НДС в рамках осесимметричной постановки задачи в сферической системе координат (r, 6, ф) будем моделировать следующими соотношениями геомет- рически линейной теории.

Уравнение равновесия:

r^" + 2(" -") = 0. dr

Соотношения Коши:

du

£ =    , £ 9 = ^£ф = .

drr

Закон Гука для внешнего слоя:

(1)                        (1)            (1) а(1) — гт(1) — 2,/?(1)(

" _г = ( ^{2 + 2 ц} 1 ) ^£ _г ^{+ 2 2} 1 ^£ 6 , " 6 = " ф = ^2£ _г ^{+ 2} ( ^{2 + ц} 1 ) ^£ 6 .

Связь между напряжениями и деформациями для внутреннего слоя:

„(2)                   (2)          (2) 2)2)-2,^2)

"г =(22 + 2ц2 )£г + 222£6 , "6 = "ф = ^2^? + 2(22 + ц2 )£6 .

Условие наличия несхлопнутых пор для внутреннего слоя:

^- ( ^£ Г ^{2) +} 2£^ ) < £ ).

Граничные условия на внешнем и внутреннем контурах запишем соответственно в виде:

СУ ( 1 ) r

г = b

^- q b , "Г²⁾

г = a

^{- q} a .

Здесь в (1)-(6) и далее " _г , "₆ , "_ф , £ _г , £₆ , £_ф - главные компоненты тензоров напряжений и деформаций соответственно, u – радиальная составляющая вектора перемещений, индекс (1) вверху компонент напряжений, деформаций и перемещений обозначает их принадлежность к

Гоцев Д.В.,                Математическая модель напряженно деформированного состояния

Перунов Н.С.                  двухслойного упругого сферического тела с учетом пористой … внешнему слою, индекс (2) – к внутреннему слою, отсутствие верхних индексов у указанных величин обозначает их принадлежность как к внутреннему, так и к внешнему слоям сферического тела.

Из решения системы (1)–(6) получим следующие НДС: для внутреннего слоя

и(2)=Г CC± Д2)=Г ?-   Д2) = Д2)=Г / u     C3r+    , br    C3       , b6    bp    C3 + r2                  r3

^r 2)= C3 (322 + 2^)-4^2 C4, ГТ    ^2) = -3 (3Л+ 2A1) + 2^1 C4;(7)

r3

для внешнего слоя

u(1) = Cr+C2 yi) = r -2-2 Д1) = Д1)=Г +C2 u Ci r+    , Cr Ci , by bp Ci + r2                 r3

^ = Ci (3Д+ 2^1)-4^1   , ^ = <  Ci (3Д+ 2ц) + 2ц C-,(8)

r3

где константы интегрирования C _i, C 2 , C ₃, C ₄, а так же у - деформированный радиус контакта

слоев, которые находятся из следующей системы граничных условий и условий совместности
	^Г2)     = - qa		C i ( 3 Л 1 + 2 ^ 1 ) - 4 ^ 1 cL = C 3 ( 3 ^ 2 + 2 ^ 2 ) - 4 ^ 2 - 4 Y^                         Y^
	1 r = a -     =- q b 1 r = b		C C 3 ( 3 ^ 2 + 2 ^ 2 ) - 4M 2 "A = - q a a
	^     = ^r2)	^-	C. C i ( 3 2 1 + 2 ^ 1 ) - 4 ^ 1 -y = - q b                    .           (9)
	1 r = Y	r = y	b 3
	u ( 1 )|     = u ( 2 )| 1 r=/           l r Y = с + u ( 2 ) ( с )	= Y	П   C4 _   C2 C 3 Y + 7=C - Y + 7 2 Y = с ( 1 + C 3 ) + C 4 1                     с

Решая систему (9) получим:

_ 4 ^ 2 с ² ( Y - с ) B (у³ - a ³) - q_aa ³ ( B ^ ³ + 4 ^ 2 с ³ ) + q b Pb³

Ci=                  AP (Y - b3)

(4^2Be2 (Y- с)(Y - a3) - qaa3 (By3 + 4^2с3) + qb^3P)b3

2                       4^i P (/- b3)

_ 4 ^ 2 с ² ( ^{Y -} с ) ^- q a ^a

C3 =

P

:³       _^{a 3} с ² ( В ( / ^- с ) ⁺ q a ^с )

, C 4 = P ’

A = 3 2 + 2 ^ _i, B = 3 2 2 + 2 ^ 2 , P = Ba ³ + 4 ^ 2 c ³ .

При этом деформированный радиус / контакта слоев определим из уравнения a _i Y 7 + aY + а ₃ /' + aY + a 5 Y + а ₆ = 0,

где

«1 = 4giP2с2 (A - B), «2 = -ц (4^2с3 (A - B) + qaa3 (A + B)), a3

= с ² ( AB ( ц ₁ a ³ - ц ₂b ³ ) + 4 ^ _i ^ ₂ ( Ba ³ - Ab ³

a4 = qaa31 ц1 Aс3 + ц1 Ab3 + 4^i^2с3 + ABb3 | - qbb31 ц1 Ba3 + 4^i^2с3 + AB a3 + ^2 Aс3 | +

+ ABс ³ ( ^ 2 b ³ - ^ ₁ a ³ ) + 4 ^ ₁ ^ ₂ с ³ ( Ab ³ - Ba ³ )

Механика а5 = AB(ц2 -ц)a3b3с2, а6 = A(ц1 -ц2)(B-qa)a3b3с3.

Объемная деформация на этом этапе для внутреннего слоя согласно (7) определится в форме f r ^{2 )} + 2 l U ^{2 )} = 3C ₃.

Тогда условие наличия в теле не полностью сжатых пор запишется в виде qaa3 < P • у + 4^2 с2 (Y - с).(12)

Следовательно, схлопывание пор произойдет одновременно во всем внутреннем слое, когда внешняя и внутренняя нагрузки будут удовлетворять условию qaa3 ^ y° + 4^2 с 2 Y - с).(13)

На втором этапе деформирования, то есть при выполнении условия (13), НДС будем моделировать соотношениями (1)–(2), присоединяя к ним граничные условия (6), реологические соотношения (3) для внешнего слоя, и соотношения

Sr2)= 2.ZL2z/r. ■ 3Uf , Sy2) = Sy2) = 2це\2) -2ц3У + 3ц^,(14)

для внутреннего.

Здесь в (14) и далее ц = ц ₂ + ц ₃, S r ^{2 )}, S y ^{2 )}, S ^² - компоненты тензора девиатора напряжений, f ^, fy'² - деформации внутреннего слоя на момент полного сжатия пор, которые определяются из соотношений (7), (10)–(12) при переходе в (12) к равенству.

Из решения системы (1)–(3), (6), (14) при условии (13) получим следующие НДС: для внешнего слоя

(1 (1)-_D Dv¹^ _f1)^__d _DE^ (1)}_(1 )}_Г) DB^

u = D3r+    , fr = D3       , LX = сф = D3 +    , r2                 r3                         r3

^ ^{( 1 )} = A • D ₃ - 4 ц • D 4 , ^ ^{( 1 )} = ^ ^{( 1 )} = A • D ₃ + 2 ц • — 4 . r             3Г1Ч x             Ф            3 г 1 з

rr для внутреннего слоя

U ²⁾= D_xr + 4 D₂

1     „2     2

^ ( 1 + ln r 11

f

f ²)= D 1 - 4 D_: r ³ I

V

С(0) ( 2цСд I —3 4 I 2ln r ц V

o r ^{2 )} = Л 2 Е 0 + 2 ^ D 1 V

2 ) ^а е

r

V

А

- 31

V

^{2 )} , ^lu

ц V 3

,

V

= f⁽ D + 4 D 2

r

V

4 ц С 3 ( 1 , )'

-ц - ⁽3^+ln r J

V

,

-2 ⁽ ^ D ₂ - Ц 3 C 4^{0 ) (} 4ln r + r ³ V                V

= о \, ²⁾= X 2 ^f 0 ^{+ 2} A D 1 ⁺ 4 r

V

( цD "2

V

Ц 3 С 4^{0 )}

3^3     ,

V

А

( 7 + 12ln r ) - Ц 3 С 3⁰

V V

,

где константы C30), C40) определяются соотношениями (10), в которых среда рассмотрена на мо- мент полного сжатия пор и имеют вид

_r( 0 )_ L₀ У0 ) _^{с 2} 1 a³B ⁽ Y ^- с ^{) +} с ( 4 Ц 2 с ^{2 (} Y ^- с ^{) +} P ^{( L} 0/ 3 ) ))

C3 = 3 , C4 =                    P константы интегрирования D1, D2, D3, D4, а так же у - деформированный радиус контакта слоев на этом этапе деформирования находятся из следующей системы граничных условий и условий совместности

Гоцев Д.В., Перунов Н.С.

Математическая модель напряженно деформированного состояния двухслойного упругого сферического тела с учетом пористой …

- .

I r = a

- q _a

f

^ 2 ^ 0 + 2 a d к

- 41 A D 2 - A 3 C 4^{0 )} I 4ln r + ¹ a 3 _{к              к} 3

A 3 CY

^- q a ,

4"| 4"

I r — b

- q_b

A • D3

D 4

4 ^А 1 • b^r ^{— -} q b ,

= ^?

I r — У

r—у

( 1 ⁽¹⁾l -M⁽²⁾l u u

Ir —y         lr —У у — с + u(2) (с)

A • D 3

4 A 1 • D = ^o + 2 A D 1

^D з У ⁺ D = D Y ⁺4 ^D 2

к

1 ~ у — с + Dc + — D c

2 ^-

к

-2- 1 A D 2 - А з C 40 ) [ 4ln r + ¹ Y к             к 3

4 ^С (0) ( 1 . к "зт ^f 3 ^{+ ln у} J ,

к

А з C 30 )

,

l                    к разрешив которую получим константы интегрирования:

12ас 2 (у - c) + 12а3 C40) [1 + 4ln c

D =кa

¹                       6 a R

^- a ³ ( F ^{+ 3} q a )

,

Dз =

a3 (6 ас 2 (у - c) + c3

D 2 =---------------

( F + 3 q _a ) ) + 4 A 3 C 4^{0 )} f 6ln ( a ^{2 c} 3 c^a 3 ) + c ³ + 2 a ³

2 c ² У 1 ( y ) ( 6 а ( у - c ) + Fc ) + 12 А з C ' 4ln к

6 A R

f cy1( y )• yR )

n 2 c3 + Y к a 7

к

,

+У1 (у) + з(qbb3R-qaa3 (2c3 + Y)) 7

³ ARy 2 ( У )

,

b ³ 2 c ² y i ( у ) ( 6 а ( У - c ) + Fc ) + 12 A 3 C 40 ) 4ln

D 4 =—

к

f cy1(y )• yR )

„ 2 c3+Y к a 7

^

+ У 1 ( у ) + з ( q b Y R

-

¹² A Ry ( y )

^

q a a ³ ( ^{2 c 3 + у} ))

,

а так же уравнение для поиска границы у контакта слоев в случае деформирования сжатого ске- лета

f

4 A 3 C 4^{0 )} 12ln

^{f А} У 1 ( ^y ) У 4 ^{( y} )^{- A} 1 Ay 2 ^{( y} ) ( ^{2 y} 3 ⁺ a 3 )     R ( АУ 4 ( У ) + A 1 Ay 2 ( У ) )

^{c                          Y}

кк

a АУ 4 ( У ) ( 2 c ³+ У ³ ) -2 AA 1 У 2 ( У ) У 3 ( У )

^

⁺ 3 А У 4 ( У ) У 1 ( У ) ^{- 6} A A 1 У 2 ( У ) У 3 ( У ) ⁺

+ c ² ( 6 а ( У - c ) + Fc ) ( 2 A y 4 ( y ) y 1 ( У ) - 2 A A 1 a ³ y 2 ( у ) ) + 2 A 1 A Y ( Fa ³ - 12 A C ² ( у - c ) ) y 2 ( y ) +

+ 3 q b A ( 4 A 1 + A ) b 3 Y 3 R + 3 q a a ³ ( 2 A 1 Ay 2 ( y ) y 3 ( y ) - A y 4 ( У ) ( 2 C ³ + Y )) — 0,

- с ³ ,

В (18), (19) приняты следующие обозначения y 1 ( у ) — Y - a ³, у ₂ ( У ) — Y - b 3 , у 3 ( У ) — Y

У 4 ( У ) — 4 A 1 Y + Ab ³ .

Таким образом, НДС двухслойного сферического тела на этапе упругого деформирования пористого материала внутреннего слоя, то есть при реализации условия (12) определяется соотношениями (7), (8), (10), а на этапе упругого деформирования сжатого скелета внутреннего слоя (при выполнении условия (13)) - формулами (15)-(18). При этом деформированный радиус у контакта слоев на первом и втором этапах деформирования находится соответственно из уравнений (11), (19).

Полученные в данной работе аналитические соотношения, описывающие НДС двухслойного сферического тела при действии сжимающих нагрузок, могут быть использованы в качестве ос-

Механика новного докритического состояния при решении задач устойчивости многослойных крепей подземных сферических полостей, а также защитных сферических резервуаров, находящихся под действием всестороннего равномерного сжатия в случае упругой работы материалов.

При проведении численного эксперимента все соотношения приводились к безразмерному виду, при этом величины, имеющие размерность напряжений, отнесены к величине р 1 , а имеющие размерность длины – к радиусу b .

Результаты численного эксперимента представлены на рис. 2 и 3.

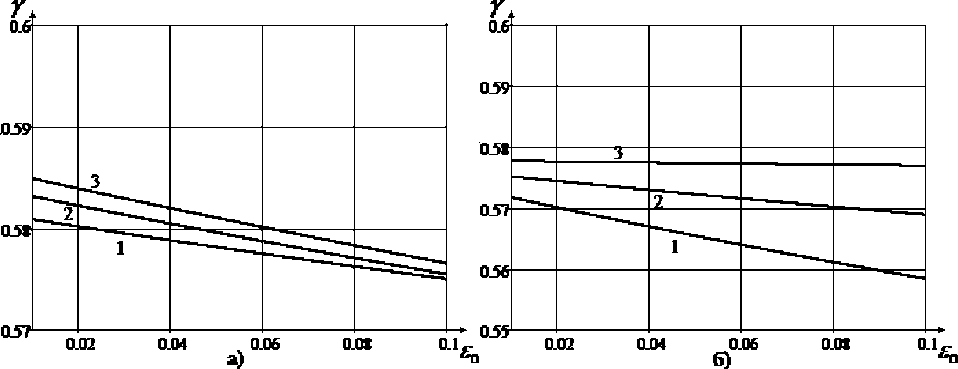
Рис. 2. Зависимость деформированной границы контакта слоев от начального раствора пор при деформировании сжатого скелета: а ) 1 - р ₂ = 3 ,2 - р ₂ = 4 ,3 - р ₂ = 5 ; б) 1 - р ₃ = 1 ,2 - р 3 = 2 ,3 - р ₃ = 3

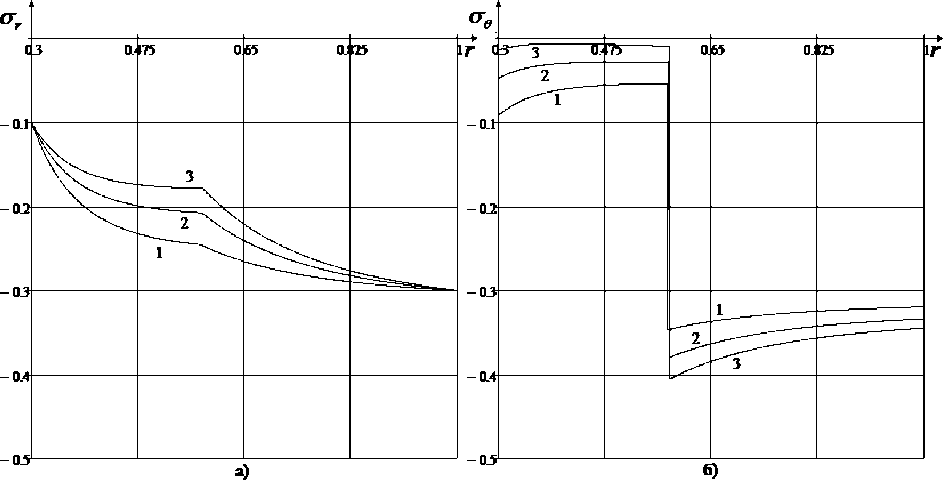
Рис. 3. Зависимость напряжений от координаты при деформировании сжатого скелета

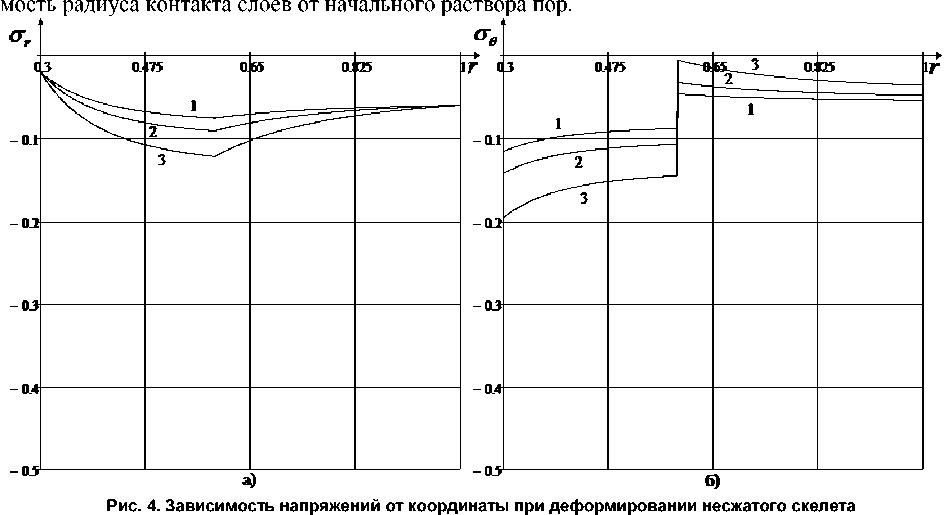
На рис. 3 и 4 кривые 1 соответствуют р 1 = 1, кривые 2 - р 1 = 2, кривые 3 - р 1 = 3 .

Безразмерные значения других физико-механических и геометрических параметров, если не оговорено особо, брались следующими q a = 0,1, q b = 0,3, a = 0,3, с = 0,6, b = 1, £ 0 = 0,02, р 1 = 1, Л 1 = 4, р 1 = 1, / 2 = 5, р ₂ = 2, р ₃ = 3 .

Таким образом, в работе построена математическая модель для описания напряженно-деформированного состояния двухслойного сферического тела с учетом пористой структуры внутреннего слоя при упругой работе материалов. В рамках предложенного подхода к деформированию пористых сред получены аналитические соотношения, описывающие НДС двухслойного сферического тела, находящегося под действием всестороннего равномерного сжатия, на эта-

Гоцев Д.В., Математическая модель напряженно деформированного состояния Перунов Н.С. двухслойного упругого сферического тела с учетом пористой … пах упругого сжатия пор и упругого деформирования тела с полностью сжатой матрицей. Выведена зависимость между внешней и внутренней нагрузками, необходимыми для полного сжатия пор во всей области внутреннего слоя. Для каждого из этапов деформирования получены уравнения для определения деформированной границы контакта слоев. При этом из анализа решений следует, что как при увеличении модуля сдвига ц2 сжимаемого скелета на первом этапе дефор мирования, так и с ростом модуля сдвига ^2 + ^3 сжатой матрицы величина деформированного радиуса раздела слоев увеличивается. Также для обоих этапов наблюдается убывающая зависи-