Математическая модель неизотермического течения высоковязких сред в каналах матрицы экструдера

Несмотря на то, что теоретическому исследованию неизотермического течения высоковязких сред с учетом диссипации энергии посвящен ряд работ, однако до настоящего времени эти вопросы изучены явно недостаточно. Осложняющими факторами моделирования подобных процессов является зависимость физико-механических свойств расплавов экструдата от температуры. В обычных условиях наиболее сильно изменяется с температурой коэффициент динамической вязкости. Поэтому ограничиваемся учетом изменения одной лишь вязкости, полагая остальные физические свойства постоянными [1-4].

Рассмотрим одномерное плоское установившееся течение высоковязкой жидкости в цилиндрическом канале. Канал имеет длину L и радиус R .

Введем цилиндрическую систему координат. Начало отсчета продольной оси z системы совместим с входным сечением канала.

Рассмотрим движение жидкости за счет разности давлений на входе P0 и на выходе из канала РL .

В поставленной задаче температура стенки канала принимается постоянной и равной Tw .

Одномерное течение и теплоперенос высоковязких сред с учетом общепринятых допущений описывается системой уравнений неразрывности, гидродинамики и конвективного теплопереноса с учетом диссипации механической энергии, которые могут быть записаны в цилиндрической системе координат следующим образом:

где ρ – плотность среды; r, z – цилиндрические координаты; Р–давление среды в канале; U– скорости частиц среды; с – удельная теплоемкость среды в канале; X - коэффициент теплопроводности среды; ^(т) -коэффициент динамической вязкости, зависящий от температуры; T   –заданные коэффициенты в пред- вх,j ставлении профиля температуры во входном сечении канала, определяемые из дополнительных условий(принятый здесь вид граничного условия для температуры при z равном нулю, как это будет следовать из дальнейшего рассмотрения обуславливается видом предполагаемого приближенного решения для температуры в канале); J – степень полинома, используемого для аппроксимации начального профиля температуры на входе в канал.

В настоящее время известно много форм представления коэффициента динамической вязкости в зависимости от температуры. Для простоты дальнейшего рассмотрения будем предполагать, что на сравнительно малых интервалах температуры изменение коэффициента динамической вязкости с достаточной степенью точности можно принять линейным. Это позволяет зависимость ^ (т ) аппроксимировать соотношением вида:

ц ( Т ) =ц 0 + Р 1 ( Т хар - Т ) ,           (3)

a и .     a^ (T) a и a p _n

= 0 ; = 0 ;

az          az ar ar д ( (тх ди) дp _

--l ц ( Т ) r ----I--= 0 ;

¹ д r l        д r J д z

дТ . 1 sfSTY ,TYdu)2 pcU— = Л--1 r— I + u.(T)l — I дz     r dr l dr )       l dr )

где ц 0 , Ц 1 - эмпирические коэффициенты, определяемые экспериментально для каждой жидкости в отдельности; T_хар – некоторая характерная температура процесса.

Для перехода к безразмерному виду введем следующие переменные, параметры, функции и критерии:

r --^; D = 2R ; z - = ^; Eu = P^L

R l L p v m

Запишем граничные условия:

^{д r} r = 0

U r = R = 0;

дТ дr r=0

= 0;

4=r = T w ;

T ( r ) z = 0 = E T ex,j f j = 0

P z = L = P L ,

j

;

'         T вх, j

1вх,j = т

T крит

'       T хар

^Тхар = _т T крит

—

—

—

^Твх,0 ; Т ‘ =

T вх,0

Т - Т вх,0

—

T вх,0

; T_w T вх,0

, P — Pl p =----------; ^j

P0 — Pl ц1 (Ткрит

Vis =--------

T крит

Tw

—

—

T крит

U и ' = —; Q =

V

—

Ц 0

^Твх,0 )

;

T вх,0

T вх,0

—

T вх,0

Q;

n R 2 v_m ’

ц c

Pr =^;

Л

;

Re = 2 p V m R

Ц

;Ec =

Vm

^{с ( т}крит ^{— Т}вх,0

)

С учетом (4) граничные условия (2) принимают вид:

где r ' - текущий радиус канала; D - вспомогательный геометрический параметр, характеризующий отношение гидравлического диаметра канала к его длине; z ' - безразмерная продольная координата; T^',T_х^'_ар, T_w^' –значения температуры; T_к^'_рит – безразмерное значение критической температуры; P ' -давление среды в канале; U ' -скорость среды; Q - расход среды через канал; Vis – параметр характеризующий отношение характерной вязкости к величине масштабной вязкости; Pr, Re, Ec, Eu – критерии Прандтля, Рейнольдса, Эккерта, Эй-

Jj

^{T (} r ) ' _n = ^ T exj ; ^z = 0 j = 0

p ' ,    = 0.

z = 1

^{d r} r ' = 0

T = т •

T , Tw;

r = 0

лера, соответственно .

Здесь и далее верхние штрихи указывают на безразмерную форму записи соответствующих величин.

Заметим, что в качестве T_к^'_рит прини-

В общем случае точное решение системы уравнений (5) с граничными условиями (6) представляется затруднительным. В этой связи рассмотрим подход к построению приближенного решения рассматриваемой задачи, в соответствии с ко-

торым распределение скорости, давления и температуры будем искать в виде разложения по степеням безразмерной поперечной координаты r^' :

мается такая температура, при достижении которой в рассматриваемом процессе возникают факторы, которые ставят вопрос о правомерности использования этой математической модели. Например, при экструзии теста его разогрев до некоторой определенной температуры приводит к денатурации белка. В других процессах в качестве Tк'рит может быть принята, например, температура фазового перехода.

С учетом (4) основные уравнения (1) могут быть записаны в следующей форме

^U = 0 ;

d z

«

U ⁽ r ) = X U j ⁽ r j = 0

*

^{P (} r ,z ) = X P j j = 0

*

T (r ,z )= X Tj j=0

;

;

Подставляя (7) – (9) в (5), приходим после соответствующих преобразований к системе обыкновенных дифференциальных уравнений относительно коэффициентов разложения P j ( z ) , T j ( z ) , как, функций продольной координаты z ,

d P '

+ d r

D d U d

Eu Re d r d z

( 1 + Vis ( тXар - t ' )) = 0 ;

Eu Re D d P

1 d

d z

r d r

~ (1 + Vis T..p

—

T ')) r^ d r

;

PrRe ' d T _ 4 1 d

'                                                     '                     '

D     d z D ² r d r

f r £1+

( dr J

4 Ec Pr         '

⁺ d 2 ^{1 + ViS} V T rop

( dU

'2

—

I dr' ,

.

и постоянных коэффициентов U j , j = 0,1,....

Рассмотрим наиболее простой частный случай, когда в соотношениях (7) – (9) допустимо ограничиться следующим числом членов разложения:

– для скорости – первыми тремя;

– для давления – первыми двумя;

– для температуры – первыми пятью.

В рамках рассматриваемого приближения с учетом допущения о параболическом профиле скорости коэффициенты разложения в (7) определяются из выражений:

U 0 = ^2- ; u 1 = 0; u 2 =- U c - (10)

В итоге после соответствующих преобразований приходим к следующей системе обыкновенных дифференциальных уравнений относительно T ₀ , T ₁ , T ₂ , T ₃ , T ₄ , P ₀ и P₁ как

Получено аналитическое решение уравнения (12):

P 0 -

C1 cos

функций продольной координаты:

< . 7

Az

V I

+ C 2 sin

( .7 A ^z

V J

x

L L' 'ti ‘ EuReD d Po 1 + V^{is (} Txap To ^{)) u}2 -             ‘

B2'

^— z + C₃ + B 0 z

3    B₁

PrReDU₀ ^ T^ O- - 16T2 ; d z

где для краткости записи приняты обозначения:

PrReD

Uo ' T + u2 d z          d z I

( ■ ай dz

z

B 0 B 2 --- n B 1 B 3 - 0       7

A² + ( B₂/B₃ ) ²

- 64 T4 + EcPr ( 1 + VisT_xar) 4                хар

;

fd PG

A d z' V

А

_— B0 ₊ B2__C

0 B1 2B3 1

- 0                 7

P 1 - 0; T - 0; T o + T 2 + T 4 - T w .

При формировании (11) с целью получения замкнутой системы уравнений были при-

—

B 2

C₃ - — e

2B3

( A • ( A Ci cos l — I + Ct Sin l —

¹ V 2 J ² V 2

—

B0

B1

;

няты во внимание уравнения, вытекающими из граничных условий для температуры по поперечной координате.

После некоторых преобразований система уравнений (11) сводится к одному диффе-

A - V 4B 1 /B 3 — ( B₂/B₃ ) ² .

Средняя температура в канале описана

ренциальному уравнению относительно рас-

пределения давления в канале:

d3P0'       d2P0'dP

BO /   + Bi / X) + B2—" - B3,

d(z')3       d(z')2dz здесь для краткости записи приняты обозначения:

Pr ² Re ³ D ³ Eu '        3PrEuRe² D²

'0 -------A--------U 0 ; Bi ------7777------’

162Vis                  16Vis

B ₂ - 64 Eu Re D

v VU + ^E c ^{Pr U} 0 ,

Г 1 1 i A

Ro = 64 T - T B3 ⁶⁴ l Tw Txap у^₈ I .

Принимая во внимание функциональные связи между коэффициентами разложения для давления и температуры, вытекающие из (11), граничные условия для уравнения (12) с учетом (6) записываются в виде уравнения (13).

После нахождения распределения давления вдоль оси продольного канала, температурное поле определяли из (9) с учетом уравнений (11).

d P0

6 z '

z - 0

'

------— (1 + Vis(r_xap

EuReD       хар

—

^Tex,0 )) ’

уравнением:

f r ' T ' ( z ' ,r ' ) u ' (r ' )dr '

T 'sr (z ' ) -                                         (15)

f r ' U ' (r ' )dr ' 0

Для моделирования процесса теплопере-носа высоковязких сред разработана программа на ПЭВМ. Расчет проведен по экспериментальным данным исследования течения расплава зерновой смеси гречихи и сои для скорости нагрузки 0,08 мм/с [5].

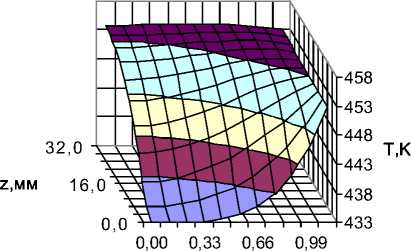
Исходные данные и результаты расчета приведены в таблице. На рисунке 1 приведено распределение температурного поля расплава смеси в зависимости от длины канала.

Из рисунка 1 видно, что при малых значениях z влияние диссипативной функции проявляется главным образом у стенки. При увеличении приведенной длины это явление распространяется на все сечение канала. При большом z профиль температур целиком определяется диссипацией. В случае теплообмена, обусловленного только теплотой трения, форма кривых распределения температур является следствием взаимодействия эффектов нагрева за счет вязкого сдвига с эффектами охлаждения за счет теплопроводности.

d²P 0 ^'

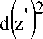
- 0^;P0

z - 0

. - 0 z - 1

r,мм

Рисунок 1. Распределение температурного поля расплава смеси зерна гречихи и сои

Методом машинного эксперимента осуществлена проверка полученных решений на адекватность реальному процессу теплопере-носа. Отклонение расчетных данных от экспериментальных по абсолютному значению не превышало 12 % (таблица 1).

Т а б л и ц а 1

Исходные данные и результаты расчета

Параметр

Значение

Радиус канала, м Длина канала, м Температура на входе в канал, К Температура стенки канала, К Характерная температура, К Критическая температура, К Скорость потока в канале, м/c Избыточное давление на выходе, кПа Эмпирический коэффициент μ 0 , кПа·с Эмпирический коэффициент μ 1 , кПа·с Теплопроводность      расплава, Вт/(м·К) Удельная теплоемкость расплава, Дж/(кг·К) Плотность расплава, кг/м3 Расход среды через канал, кг/м3 Число Vis Число Прандтля Число Рейнольдса Число Эккерта Число Эйлера

0,0011 0,0320 433 453 443 459 0,8·10-4 31,00 11,1 0,240 0,220 1600 1200 1,157·10-8 0,562 8,073·107 1,189·10-5 6,01·10-8 1,167·104

Выводы:

• 1.    Выявлен характер изменения поля температур высоковязких сред в различных сечениях цилиндрического канала.

• 2.    Полученная модель позволяет с достаточной точностью (±12 %) рассчитать не только значения температур высоковязких сред в цилиндрическом канале, но и провести анализ влияния основных параметров системы на характеристики диссипативного разогрева материала.