Математическая модель низкотемпературного воздействия на биоткани

DOI:

Математическое моделирование тепловых процессов, возникающих при низкотемпературном воздействии на биоткани, является важным инструментом анализа в приложении для различных областей медицины и биотехнологий [13; 34–36]. Особо следует выделить применение математических методов с целью повышения эффективности медицинской диагностики на основе радиотермометрии [21; 37]. Это связано с развитием новых криогенных технологий и использованием их в разных областях человеческой деятельности.

Имеется целый ряд математических моделей, описывающих тепловые процессы в биологических тканях. Однако возникает проблема создания новых математических моделей для моделирования фазовых переходов, возникающих при воздействии низких температур на биологические ткани. Эти модели требуют разработки численных алгоритмов для их решения и создания соответствующих программных продуктов.

Математическое описание тепловых процессов с фазовыми переходами, восходит к работам Г. Ламе и Б. Клайперона. Развитием стала модель Йозефа Стефана [39], позже названная «задачей Стефана» [29; 30]. Среди работ, посвященных вопросам разрешимости задач с фазовыми переходами, можно выделить работы А.А. Самарского, О.А. Олейника и др. [9; 10; 23; 24; 30].

Основные теоретические результаты, связанные с изучением нелинейных процессов теплопроводности в активных средах с источниками или стоками, зависящими от искомых полей получены в работах: А.А. Самарского, С.П. Курдюмова, Г.Г. Еленина, А.П. Михайлова, В.А. Галактионова, К.Б. Павлова, Л.К. Мартинсона, А.Н. Тихонова, Н.С. Пискунова, О.А. Олейника, О.А. Ладыженской, Т.Д. Вентцеля, В.П. Маслова, М.И. Вишика, С.И. Похожаева, А.С. Калашникова, С.Н. Кружкова, С.Н. Антонцева, Ж.-Л. Лионса, Ф. Браудера, Х. Брезиса [1; 2; 9; 10; 14; 20; 22–24; 27; 28; 31; 33; 38].

Цель данной работы является изучение динамики температурного поля биологических тканей при низкотемпературном воздействии на биоткани криозондом со сферически — симметричной формой аппликатора с использованием численных методов.

1. Постановка задачи

Для охлаждения или замораживания биологических тканей используются инструменты со сферическими и полусферическими формами аппликаторы. В качестве приложения укажем на задачу разрушения тканей в медицине [3; 5; 6; 11; 37]. Указанная форма аппликаторов позволяет изучать динамику температурного поля биологических тканей на основе решения следующей задачи со свободной границей [12; 16; 17]:

ди ихх - Х2 [к + (1 - к) п (х - и)] — = ^х1 вивп (х — и),  1 < х < s (t) , t > 0, и (х, 0) = 0,   1 < х < s (0), ди                                             ,             ,,                     , ,         ,             ,          ,

---[Н +(h — Н) п (1 — и)] и = —g (t) + (1 — y) РП (и — 1), х = 1, t> 0,   (1) ох и (s (t) ,t) = 0,        S ' , t> 0, дх

^[<* =°,   [ охL = ^х"^Рх' , '> °,

Используются следующие обозначения:

,               aro           T — TA h = 1 + p, p = T, g (t) = h-=——

Л ck mk T1 e и = —-----jtr , Н = 1 + PY, Y = г,

( t — T *)1 e к = а, ср

р - л       - /¥ с (Т - Т*) ’   X VA Г°’

Т = 36,6 °C, Т * = 0 ± 3 °C, Та — температура аппликатора криозонда, Л, с, р, Л — являются теплофизическими характеристиками биологической ткани, c _k , m _k — теплоемкость и скорость массы крови; х > 0 — означает параметр выхода на заданный режим охлаждения; β является параметром нелинейности. Знак черта над или под символами обозначает соответственно незамороженную или замороженную области биологической ткани, [ ] _ж * — означает скачок соответствующей функции.

В задаче (1) определению подлежат температурное поле и = и(х,у), свободная граница s = s(t) и граница раздела фаз х * = x*(t).

Стационарная задача, которая соответствует задаче (1), при в = 0 имеет точное аналитическое решение

/ \                   \ ^(и - ^х* ) т             *

и (х) = и + (1 — х) (—*---—, 1 < х < х , и (х) = X- (2s + х*) (s — s2) , х* < х < s,

где

—    * . Н ^{( ф} - ^х * ) ^{( х} * - 1)         ^—9^ + ^{(1 — y)} ^

^и = ^{х +}           ^, ф =----- А ----,

1 + Н (х* — 1)                 Н ах* и s являются положительными решениями следующей нелинейной системы

х * — X (2s + х) (s — х * ) ² = 0, 6

2     *2 , 2Н (ф — х*) , , n п s 2 —х + X Jj + н /<х * — 1> = °. Пусть х *(0) = 1,1, s ° = 1,1 — начальное приближение,

(3)

F 1 (х * , s) = х * + A (2s + х * ) (s — х * ),

F ₂ (х * , s) = s ² — х * 2 + В (ф — х * ) (х * — 1)

гдеА = — * 2 ,В = 2М .

Согласно методу Ньютона [1; 3; 7; 24–26; 30; 37], получаем:

__1 = 1 — a (s + 2х*),  —1 = А (4s — х*), дх*ds dF2        .    „ ,    .          .dF

— — —2х + В (— 2х + ф — 1),  —— — 2s.

дх*

_{Д х} * (°) = Д = — 2,42 + 3,3АВ (ф — 1,1)0,1

х Д 2,2 + 10,23В — 3,3Вф ’ д (°) _ Д2 _ Вф — 3,31В + 0,33А6ф — 0,3АВ — 2,42

^s = J =        2,2 + 10,23В — 3,3Вф

Если для е = 0,0001 выполняется неравенство max (|Ах *⁽⁰⁾| , | As ⁽⁰⁾ |) 6 е, то вычисления заканчиваются. Если неравенство max (|Ах *⁽⁰⁾ | , | As ⁽⁰⁾ |) 6 е не выполняется, то тогда х *⁽⁰⁾ = i *⁽¹⁾ , s ⁽⁰⁾ = s ⁽¹⁾ и строим новую систему уравнений. Аналогичный процесс проводим для последующих итераций.

Начальное приближение определяем графическим способом и в качестве начального приближения можно взять х ⁽⁰⁾ = 1,1, s ⁽⁰⁾ = 1,2.

Применяя метод итерации, процесс вычисления неизвестных границ строится по следующим формулам:

х *^(к+1) = _А ( 2s ^{( k )} + х *^(к) ) ^8 ^{( к )} - х^^² ,

s ^(k+1) = ± (х *^(к) ) ² — В (ф — х *^(к) ) (s^") — х *^(к) ) ² , к = 0,1,...

Итерационный процесс продолжается до тех пор, пока изменения всех неизвестных на двух последовательных итерациях не станут малыми в соответствии со следующим неравенством:

х ^(к+1) — х ^(к) <  е , i = 1, 2,...,п.

Для определения условия сходимости используется принцип сжатых отображений.

2.    Интегральные уравнения для задачи гипотермии

Для описания динамики охлаждения биологических тканей поставим следующую задачу со свободной границей:

дХ2 — Iti =^2х1-вмв, 1 <х 0, и (х, 0) = 0,   1 < х < s (0), ди

• —hu = — Аф (t), х =1, t >  0,                       (4)

дх

, , , ч               ди (s (t), t)

и (s (t) ,t) = 0, ------------= 0, t> 0, дх где ф (t) = ^.

Асимптотическая устойчивость решения задачи (4), позволяет искать решение в виде суммы и (х, t) = и (х) + и (х, t), где и (х) является решением соответствующей стационарной задачи с s (t) = s = const. Функция и (х, t) является решением следующей задачи:

д2и   ди дх2 — ^ = F (х,и) ’ 1 <х 0, и (х, 0) = и0 (х),   1 < х < s (0), ди                  ,

• —--ди = — дф (t), х = 1, t >  0,                        (5)

дх и (s (t) ,t) = —и (s (t)) ,                 = —'             , t> 0, дх           дх

Пусть выполняется $ ^ 1 (h ^ 1). Тогда верно равенство v (1, t) = ф (t). Решение задачи (5) будем искать в виде суммы тепловых потенциалов [8; 18; 19; 21]:

V (x,t) = /"^ G (x,t; t, 0) v o (t)dt + [ ¹ — ⁽ ^'t ^{;1,t , )} ф (t')dt'+ 1                               0        ^{d t}

+ [     G (x,t;s (t') ,t')^ (t') dt + / [     G (x,t; t,t' ) F (t,v)dtdt'

J 1                                        0 71

где

G (x, t; t, t ' ) = G _o (x — 1,t; t - 1, t ' ) — G _o (1 — x,t; t — 1, t ' ) ,

G o (x, t; t, t ' ) =

i           _      2

—,            e 4 ( ‘-‘‘ ) .

2 У П (t — t ' )

Для любой дифференциальной плоскости и подлежащей определению функции s (t) уравнение (6) удовлетворяет дифференциальному уравнению, начальному условию и краевому условию и (1,t) = ф (t) искомой задачи (5). Если потребовать, чтобы выполнялись оставшиеся условия задачи (5), то получается следующая система интегральных уравнений:

У G (s (t) ,t; t, 0) v o (t)dt + У G t (s (t) ,t;1,t')dt'+

+ / G (s (t) ,t; s (t ' ) ,t^r) ^ (t'^dt' + f /     G (s (t) ,t; t,t'') F (t,v)dtdt' =

J1o 71

= ^{—u (s ( t )) ,}

^ + f G . (s (t) ,t;t, 0) v o (t)dt + [MtlBф (t)d_t ' +

• 2       1                                     1

+ Г * д^з^у.;^^^ ^ (t ' )dt ' —

. 7"            dx(9)

• —    ,* ,.(o)                         , (f —

o 1

[ * H^{o) dG (s (t) ,t} ; ^{s (t} ) ,t')                       ^{du (s ( t ))}

• ^—    Z /1   ------ dx------ ^{F ( t} , ^{v ) dtdt} = —.

Таким образом, имеем уравнения (6)–(9), которые образовывают замкнутую систему нелинейных интегральных уравнений для определения v (x,t), ^ (t) и s (t).

Для поиска неизвестных и = и (x) и s требуется решить стационарную задачу [1].

Далее, для поиска пары и = и (x) и s применяется функция Грина. В итоге получается нелинейное интегральное уравнение Вольтера [8; 15; 18; 19]

и (x) = х² J' (t — x ) U (t)dt

и нелинейное уравнение

X ² J [1 + h (t — 1)] и ^в (t) t ^{1 e} dt = hq.

Если в = 0, то получается и (x) = — (2s + x) (s — x)2 .

Если 0 6 в < 1, то (10), (11) не имеет точного решения, поэтому ее приближенное решение ищется в виде и = A (s — x)e ,

где параметры A, s , b относятся к неизвестным и их требуется тоже определить.

В случае, когда в = 0, получаем:

1 2^П

г ^ f⁰) (       Г

Ji r^p[

( s (t) — Е) ² 4t

j — exp [

⁽2 - ^{s ( t )} - Е)

1 Г s (t) — 1 ⁺Vn Z (t—^T^exp

I

( s (t) — 1) 2 4 (t — t ‘ )

4t j ф (t ‘ )dt ‘ +

]} и m+

1      r *

^p 2^ J_o

— exp

-

---3 ^exP • t ‘ ) ²

⁽² - ^{s ( t )}

exp

-

4(t - Л

H^{( t )}

-

+ [2 —

■—

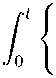
(t — t ’ ) ³/²

( s (t) — 1) 2 4 (t — t ‘ )

^ (t) dt ‘

| [^{s ( t ) — E ] ex}p [

s (t) — Е] exp

-

-

( s (t) — Е) ² 4t

■

(2 — s (t) — Е)2"| ]            ।

4t           ^{и ( Е ) d E} +

( s (t) — 1) 2

--------77? exp

2 (t — t’)³/²

^{s ( t ) — s (t}T

4(t — 1 ‘ )

+

■ ^[2 — ^{s ( t )} — ^{s ( t} ‘ ^)] exp [^—“      ^4^   ~ ~j | ^^{( t ) dt} = — ^u . ^{( s ( t ))}.

Определив из системы функции ^ = ^ (t) u s = s (t), c помощью квадратуры (6) (F (Е, v) = 0), находим v (x, t), 1 < x <  s (t), t >  0.

Относительно h (t) система (14), (15) является системой интегральных уравнений Вольтера. Поскольку неизвестная функция s = s (t) входит в систему сложным образом, то вопрос разрешимости данной системы остается открытым. Полагая t = T , получаем, что при T ^ то , первое из данных уравнений системы обращается в тождество, а второе уравнение системы преобразуется к виду:

H (T) + 2 Г G . ( s (T), T ; s (t ' J X) н (i ' )dt = 0.

Согласно (6) v (x, T ) ^ 0, и поэтому и (x, T ) ^ и (x), при T ^ то .

Применение конечномерной аппроксимации дает систему из нелинейных алгебраических уравнений для определения узловых значений U i = и (x _i ) и числа к.

Использование программного комплекса для ЭВМ «Сферически — симметричная гипотермия и криодеструкция биологической ткани в медицине» [16], позволяет определить режимы охлаждения, динамику температурного поля в случае 0 6 в < 1 и визуализировать температурные поля.

Проведены численные расчеты на ЭВМ с применением разработанного программного комплекса. Результаты расчета представлены на рисунках 1, 2.

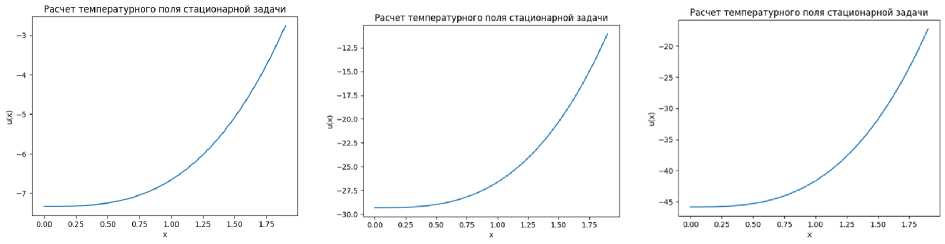
а) в = 0 , Н = 1 , fi = - 10

б) в = 0 , Н = 1 , fi = - 15

в) в = 0 , Н = 1 , fi = - 20

Рис. 1. Распределения температурного поля (стационарный случай), показанные для трех случаев: а), б), в)

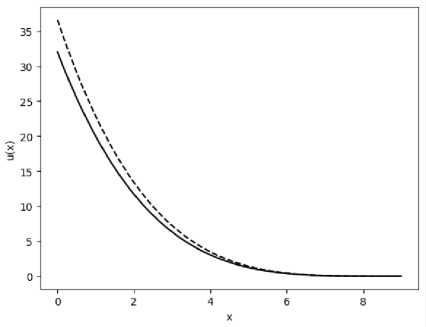
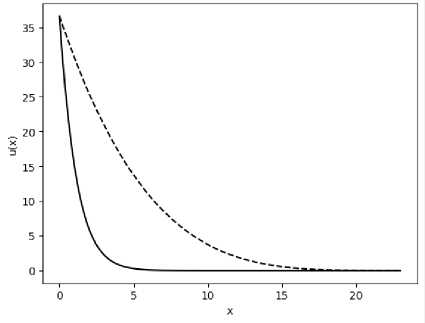
Рис. 2. Примеры расчетов температуры 0 6 в <  1

Заключение

В работе построены модели для расчета характеристик биоткани при воздействии на них низкой температурой. Описанные методы решения одномерных задач позволяют установить функциональные зависимости основных параметров низкотемпературного воздействия на биоткани от входных данных, рассчитать глубину криопоражения, замораживания и охлаждения, скорость замораживания, необходимую экзпозицию криовоздействия.

Предлагаемые в работе подходы можно использовать помимо криомедицины также в химических технологиях, строительстве, при решении задач, возникающих при добыче нефти и газа и в других областях.