Математическая модель образования кристаллических зародышей в переохлажденном расплаве эвтектического сплава

Ввиду сложности явления исследователи обычно выделяют один из процессов, например, рост частиц новой фазы, а протекание остальных процессов постулируют какими-нибудь простыми соотношениями. При этом учитывается влияние этих процессов на выделенный процесс, но не учитывается влияние выделенного процесса на остальные процессы (что изменило бы их течение и, в свою очередь, течение выделенного процесса).

Наиболее распространены теоретические методы математического моделирования процессов кристаллизации в расплаве, разработанные М. Авраами [1–3] и А.Н. Колмогоровым [4]. Эти методы позволяют получить уравнение зависимости доли кристаллов в расплаве от скорости их роста, интенсивности образования и от времени протекания процесса, что дает возможность рассчитать скорость и время протекания процессов кристаллизации в переохлажденном расплаве. При этом уравнения интенсивности зародышеобразования и скорость роста кристаллов задаются произвольными простыми зависимостями от температуры расплава, времени протекания процесса и различных физико-химических характеристик расплава.

Применение методов Авраами и Колмогорова ограничено рядом допущений. В частности, они не позволяют учитывать динамическое изменение характеристик расплава (к примеру, изменение концентрации компонентов или температуры), обусловленное процессами образования и роста в расплаве кристаллов различного состава. Это не позволяет применять методы Авраами и Колмогорова для описания эвтектической кристаллизации многокомпонентного расплава, когда возможно одновременное образование кристаллов фаз разного состава.

Таким образом, требуется разработка методов, которые комплексно описывали бы протека- ние процессов кристаллизации при затвердевании переохлажденного эвтектического расплава, учитывая динамически изменяющиеся факторы. Трудность их разработки заключается в сложности получаемых зависимостей. Однако в связи с развитием вычислительной техники появилась возможность решения таких сложных уравнений численными методами. Подходы к построению и решению таких уравнений создаёт теория зарождения новой фазы при протекании гетерофазных химических реакций [5, 21–38], которая позволяет учитывать и особенности процессов кри- сталлизации в многокомпонентных расплавах.

Цель работ. Создание математической модели процессов кристаллизации при затвердевании переохлажденного эвтектического расплава, учитывающей динамическое изменение характеристик расплава. Теоретическое описание таких процессов приобрело большое значение в связи с развитием производства металлов в аморфном состоянии методом закалки расплавов [6].

Методика. Имея в виду применение изучаемых закономерностей к процессам аморфизации эвтектических сплавов типа Fe _x B_{1 - x} , рассмотрим двухкомпонентный расплав компонентов A и B. При охлаждении такого расплава возможно выделение кристаллов чистого компонента A и химического соединения A B   ( n и n –

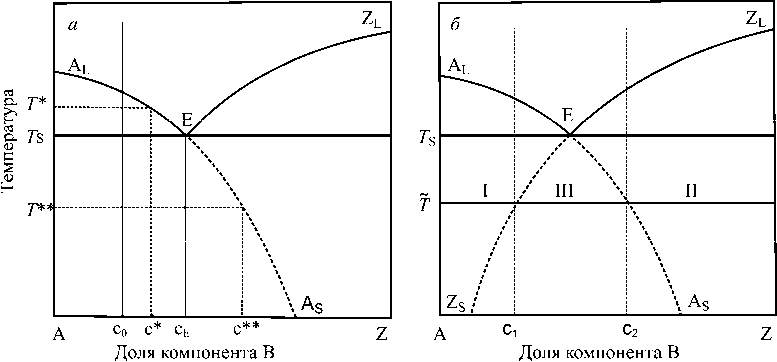
Рис. 1. Модельная диаграмма состояния двухкомпонентной системы: а – неполная диаграмма; б – полная диаграмма

AB соответствующие стехиометрические коэффициенты), которое мы для краткости будем обозначать символом Z . Пусть система обладает простейшей эвтектической диаграммой (рис. 1, а) с эвтектической точкой E. Линии ALE и ZLE определяют равновесие между расплавом и чистыми веществами A и Z соответственно.

Рассмотрим случай, когда расплав с долей c 0 компонента B (меньшей c E ) медленно охлаждается до температуры T ^*. В результате равновесного охлаждения мы получили бы твердую фазу A и раствор состава c ^*. При кристаллизации расплава со значительной скоростью общее равновесие не соблюдается. Но так как скорость перескока частиц из расплава на поверхность кристаллического зародыша значительно превосходит скорость диффузии компонентов в расплаве, можно говорить о локальном равновесии у поверхности зародыша. Поэтому в случае моментального переохлаждения расплава и появления в растворе зародышей компонента A можно считать, что на их поверхностях будет реализовано локальное равновесие, т.е. у поверхности расплав будет иметь (без учета поверхностных эффектов) состав c ^*. Полное равновесие установится лишь позднее, когда зародыши компонента A вырастут в макрофазу.

Таким образом, равновесные диаграммы состояния могут быть использованы и при неравновесном охлаждении. При этом линии на диаграммах показывают состав расплава в непосредственной близости к зародышам новых фаз.

Продолжая подобные рассуждения, можно рассмотреть случай моментального охлаждения расплава и ниже температуры TS. И в этом случае у поверхности кристаллических зародышей установится локальное равновесие с расплавом. Как видно из рис. 1, а, в соответствии с линией ALE чем больше переохлаждение, тем более расплав у поверхности зародыша обеднен компонен- том A и обогащен компонентом B. Следует ожидать, что при моментальном переохлаждении расплава до температуры ниже TS это изменение будет продолжаться в соответствии с некоторым гладким продолжением линии ALE в область низких значений температуры. Так при температуре T** образующиеся зародыши компонента A будут находиться в динамическом равновесии с расплавом некоторого состава c**.

Аналогичные рассуждения могут быть проведены и для заэвтектических расплавов, только выделяться здесь будут зародыши фазы Z.

Используя эту методику, продолжим линии ALE и ZLE в область низких значений температуры и получим диаграмму состояния, изображенную на рис. 1, б. Диаграмма отражает локальное равновесие выделяющихся кристаллических фаз A и Z c окружающим их пока еще незакристал-лизовавшимся раствором.

При мгновенном переохлаждении расплава до температуры T в расплаве, в котором валовая доля компонента B меньше c 2 , будут выделяться зародыши фазы A, окруженные раствором состава c 2 . В растворе, в котором валовая доля компонента B больше c 1 , будут выделяться зародыши фазы Z, окруженные раствором состава c ₁. Таким образом, в соответствии с диаграммой на рис. 1, б для температуры T все растворы можно разделить на три группы:

• 1)    растворы с валовой долей компонента B меньшей c 1 . Здесь при температуре T могут выделяться лишь зародыши фазы A, окруженные раствором состава c 2 ;

• 2)    растворы с валовой долей компонента B большей c ₂. Здесь при температуре T могут выделяться лишь зародыши фазы Z, окруженные раствором состава c 1 ;

• 3)    растворы с валовой долей компонента B большей c 1 и меньшей c 2 . Здесь при температуре T могут образовываться и зародыши фазы A и зародыши фазы Z. Реальная картина процесса будет определяться кинетикой зарождения и роста зародышей.

Рассмотрим теперь процессы, происходящие в переохлажденном расплаве с течением времени. Предположим, что расплав состава c большего c 1 , но меньшего c 2 переохлажден до температуры T . В расплаве могут образовываться зародыши фаз A и Z, причем в зависимости от кинетических характеристик системы будут образовываться либо зародыши одной из фаз, либо обеих. Пусть в расплаве образуется больше зародышей фазы A. Тогда по мере образования и роста зародышей фазы A расплав вблизи них будет обедняться компонентом A, его состав будет смещаться в сторону c 2 . В конце концов, система перейдет в состояние, при котором образование зародышей фазы A может прекратиться. При этом возможно два случая:

• а)    зародыши второй фазы Z к этому моменту так и не начнут выделяться – процесс зародышеобразования при данной температуре остановится;

• б)    еще до этого момента начнут выделяться зародыши второй фазы. В этом случае будет образовываться эвтектика.

В случае быстрого непрерывного охлаждения расплава картина процесса усложняется. В зависимости от преимущественного выделения зародышей каждой из фаз при соответствующей температуре возможно колебательное изменение состава охлаждаемого раствора, например, выделение вначале зародышей фазы A, затем фазы Z, потом опять A и так далее.

Используемая математическая модель [5, 7], модифицированная применительно к рассматриваемому случаю, учитывает следующие факторы:

• а)    образование зародышей новой фазы;

• б)    их дальнейший рост;

• в)    связанное с этим изменение концентрации компонентов расплава.

Математическая модель

Уравнения интенсивности образования зародышей A: < 2                    1/, ,'2/ qAc = TT-A- I , KA = (^Y3 (vA )/3 Ya kkT, £a = -A , 13lnEa )                 V '     ' KA

A G ( q A ) = ^kT I - q A ln £ a + ^A³

„ _     . 1 — С

P a = 4 ⁿ R Ac D P N a .. , M A c

G 2 = q K q

J A = N 0 ^pA

G? _ex J ^A G ( q Ac ) 1 A 2 n p I      kT '

I

7

Уравнения интенсивности образования зародышей Z:

^qZc =

n A n B

*_кт , £ = а ^a B , Z    K_Z

(            %1

P z = ^{4 n R}Zc Dp' ^P N a ( ( 1 ^{— С} ) M Z ^— M A n A

,

^GZ = 9 K / q / ■

J Z = N 0 ^pZ

GeJ Д°(qzc) 1

I

l

где q - число молекул в зародыше, qc - число молекул в критическом зародыше, к - коэффициент поверхностной энергии, v - удельный объем зародыша, у - межфазное натяжение на границе зародыш – расплав, k – постоянная Больцмана, T – температура, a – активность соответствующего компонента, £ - пересыщение раствора по соответствующему зародышу, K - константа равновесия химической реакции образования зародыша, AG(q) - изменение энергии Гиб- бса при образовании зародыша из q молекул, p – вероятность присоединения частицы реагента к поверхности критического зародыша, Rc – радиус критического зародыша, D – коэффициент диффузии компонента B в растворе, р - плотность, Na - число Авогадро, c - массовая доля ком- понента B в растворе, M – молекулярная масса компонента, J – интенсивность образования зародышей, N0 - исходное число молекул в растворе, G2 - вторая производная от AG (q).

Уравнения, определяющие скорость роста частиц A:

¹ — c s = K a e^xP

2K£

1 ³ q A ³ J

b_A = 4nR_ADN_aр ^У c-c^ . A A a    M_Ac

Уравнения, определяющие скорость роста частиц Z:

( 1 ^— c s ) n A ^csn^B = K Z ^exP

2 k^

1 ³ q A ³ J

,

^bZ = ^{4 n R}Z^DNa P ^T

^{c — c}S

Mz (1 — cf ) — Ma

где c_s – массовая доля компонента B у поверхности растущей частицы, b – скорость встраивания одной молекулы реагента к растущей частице.

Уравнения распределения частиц по размерам:

dNA d(NAbA ), x

+---5----= 0, qg(qbA,“), d td дN д(N^b )       /\

+ V/V= 0, qG(qbz,те), д t д q                x'

kTIAkTI

NbA =    7777 v Nbz =г, pag (qbA)          PzG (qbz)

где qb – граничный размер частицы, начиная с которого она подчиняется уже не микро-, а макрозаконам, N (t, q) - количество зародышей в системе, Nb = N (t, qb) — количество зародышей граничного размера, G' - производная AG (q).

Уравнения баланса компонентов системы: те                                 те

NA (t )=No (1 - са^)- J na (t, q) qdq - nA J Nz (t, q) qdq, qb,A те

NB (t )=No сам- ns J Nz (t, q) qdq, qГZ c = NAMAI (NAM A + nBmb ),(20)

где c ₀ ^м – исходная мольная доля компонента B в расплаве.

Начальные условия:

na(0,qA)=0,Nz(0,qz)=0 (qbA ^qA <те, qbz ^qz <те) •

Для определения констант равновесия химических реакций при образовании зародышей, фиксируя значения AhFe = 12,35 кДж/моль и AhFe3B = 67,9 кДж/моль [8] в эвтектической точке ce = 0,17(ат.), Te = 1447 K, на основе выведенной полуэмпирической формулы

f A h l Те"!. )

R TT

V ^ ¹¹ e 7

рассчитывали значения констант равновесия для переохлажденного расплава:

(                              (     1447-T1 z x

K _F e 3 B = 0,0972exp I - 5,364------- I , K Fe = 0,83exp I - 1,03------- I (23)

По уравнениям математической модели была построена соответствующая разностная задача, которая решалась на компьютере.

Расчеты

Изложенная модель предполагает моментальное охлаждение расплава до заданной температуры, что практически недостижимо. Поэтому целью изложенных далее расчетов был анализ общих закономерностей кристаллизации в переохлажденном расплаве. С другой стороны, при задании функции изменения температуры в выбранном микрообъеме расплава разработанная методика может быть применена для широкого круга технологических процессов. Так в работе [9] проводился расчет для изучения процесса получения аморфной ленты методом спинингова-ния расплава на медный барабан.

Использованные значения параметров приведены в таблице. Методика выбора физикохимических параметров системы обсуждалась в [7, 10].

Принятые в расчётах физические характеристики системы

Физико-химические характеристики для расплава
1. Предэкспоненциальный множитель в уравнении для коэффициента диффузии D 0 , м2/с	6,297∙10–7 (на основе [11])
2. Энергия активации диффузии бора в расплаве Fe–B, Дж/моль	80 000 (на основе [11])
Для зародышей железа в расплаве Fe–B
3. Межфазное натяжение, Дж/м2	0,204 [12]
4. Удельный объем твердого железа, м3/кг	1,376462∙10–4 [13]

5. Молярная масса железа, кг/моль	55,85∙10–3 [14]
6. Теплопроводность твердого железа при температуре 1400 К, Вт/(м∙К)	31,5 [15]
7. Температуропроводность твердого железа при температуре 1400 К, м2/с	6,6∙10–6 [15]
8. Энтальпия кристаллизации железа, Дж/моль	–12 350 [16]
Для зародышей Fe 3 B в расплаве Fe–B
9. Межфазное натяжение, Дж/м2	0,3 [17]
10. Удельный объем твердого бора [м3/кг]	4,248∙10–4 [18]
11. Молярная масса бора [кг/моль]	10,82∙10–3 [14]
12. Удельный объем твердого Fe 3 B, м3/кг	1,398601∙10–4 [19]
13. Теплопроводность твердого Fe 3 B при температуре 1400 К, Вт/(м∙К)	34 [20]
14. Температуропроводность твердого Fe 3 B при температуре 1400 К, м2/с	2,02∙10–5 [20]
15. Энтальпия плавления, Дж/моль	–67 900 [8]

Расчеты выполнены для значительных переохлаждений расплава эвтектических ( c ₀ ^м = 0,17) и околоэвтектических составов системы Fe–B. Расчет выполняли до момента 90 %-ной кристаллизации расплава. Для каждого момента времени рассчитывали количество образующихся в выбранной массе расплава (1 кг) зародышей каждой из фаз и определяли среднее расстояние между зародышами.

Результаты расчетов отражены на рис. 2. С первого момента начинается интенсивное образование зародышей кристаллов Fe и Fe 3 B. Образующиеся зародыши растут и к моменту времени 10 ^{- 3} с масса их становится ощутимой – доля закристаллизовавшегося расплава начинает расти. Интенсивность образования зародышей Fe вначале больше, чем интенсивность образования зародышей Fe 3 B. Выведение железа из жидкой фазы превышает выведение бора и, начиная с момента 10 ^{- 3} с, доля бора начинает ощутимо увеличиваться. В расплаве формируются более благоприятные условия для зарождения кристаллов Fe 3 B – интенсивность его образования начинает превышать интенсивность образования кристаллов Fe. Величина среднего расстояния между зародышами ( δ ) может дать информацию о расстояниях между слоями фаз в эвтектике.

С увеличением переохлаждения расплава увеличивается вязкость расплава, и, следовательно, уменьшаются коэффициенты диффузии компонентов. Условия для роста кристаллических зародышей существенно ухудшаются. При весьма больших переохлаждениях (до 750 К) образуется большое число (~1017 кг–1) зародышей, которые не могут вырасти до размеров более 0,01 мкм. Такие за-

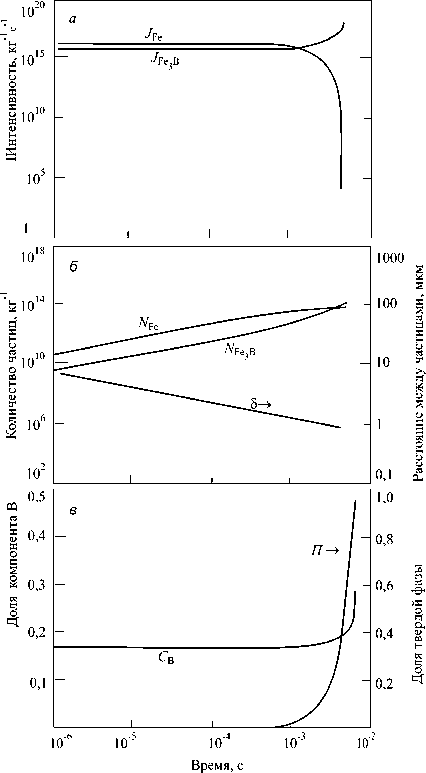
Рис. 2. Кинетика кристаллизации переохлаждённого до температуры 1000 К расплава системы Fe–B с содержанием бора 17 % (моль): N – количество зародышей, J – интенсивность их образования, δ – среднее расстояние между ними, П – доля закристаллизовавшегося расплава, C B – концентрация бора в расплаве

родыши сложно называть кристаллами, можно утверждать, что расплав затвердевает в аморфном (нанокристаллическом) состоянии.

Проведенный расчет позволил определить среднее расстояние δ между растущими зародышами, что, в принципе, можно сопоставить с размером эвтектической структуры.

Выводы

• 1.    Выполнено математическое описание процессов зарождения и роста зародышей в переохлажденном эвтектическом металлическом расплаве. Разработанная математическая модель позволяет учитывать влияние изменяющихся параметров системы на процессы образования и роста кристаллических зародышей в переохлажденном расплаве.

• 2.    По уравнениям математической модели проведены расчеты затвердевания переохлажденного эвтектического расплава Fe–B для различных переохлаждений и концентраций бора. Выявлены закономерности кристаллизации при затвердевании переохлажденного эвтектического расплава.