Математическая модель оценки электродинамических свойств поля излучения рупорной антенны в ближней зоне

Природа наделила организмы удивительной способностью использовать природные электромагнитные излучения микроволнового диапазона для поддержания своего гомеостаза [1]. Эти излучения, как правило, связанные с изменением внутренней энергии нагретых тел, характеризуются широким спектром излучения с длиной волны от долей миллиметра до десятков сантиметров и низкой интенсивностью (менее 10 мВт/см²). Указанная выше особенность взаимодействия организмов с электромагнитными излучениями природного происхождения послужила основой разработки новых физиотерапевтических технологий для коррекции нарушений регуляторных функций в организме человека [2]. Исследования последних десятилетий по оценке эффективности этих технологий доказывают высокую значимость их применения при автономном и комплексном (вместе с медикаментозными средствами) лечении широкого спектра заболеваний человека [3]. За внешней простотой применения разработанных физиотерапевтических технологий, не требующих в большинстве случаев специальной подготовки, проблемными остаются вопросы учета электродинамических свойств используемых электромагнитных излучений. В первую очередь это относится к оценке интенсивности используемого электромагнитного излучения и особенностям изменения его электрической и магнитной составляющих в ближней зоне излучения. Если в отношении интенсивности электромагнитного излучения имеет место ориентировочная информация (она указывается изготовителем физиотерапевтического оборудования), то для распределения векторов напряженности электрического поля E и магнитного поля H информация, как правило, не приводится. В совокупности это может приводить к ошибочным обобщениям в отношении механизмов взаимодействия организмов с электромагнитными излучениями. Именно этим обусловлена актуальность разработки математической модели (ММ) оценки электродинамических свойств электромагнитного излучения в ближней зоне. Использование этой модели для конкретного вида излучателя позволит расчетным способом оценивать параметры электромагнитного излучения при исследовании взаимодействия электромагнитных излучений с биологическими объектами. В практике исследований эффективности физиотерапевтических технологий широкое применение получили рупорные антенн (РА), так как их отличает компактность конструкции, достаточно широкая полоса согласования и удобство подключения к измерительной аппаратуре.

Электромагнитное поле рупорной антенны в ближней зоне

Экспериментальные исследования влияния поля излучения РА на объекты, расположенные в ближней зоне, должны учитывать точные характеристики электромагнитного поля излучения в заданном частотном диапазоне. Квалифицированный анализ такого влияния и обработка полученных результатов, основанные на контроле плотности потока мощности, требует детального определения всех составляющих вектора Пойнтинга в ближней зоне, характерной особенностью которой является необходимость использования строгих электродинамических соотношений.

Для исследования поля излучения пирамидальной РА в ближней зоне используем результаты строгого электродинамического решения задачи возбуждения секториальной E -плоскостной РА и секториальной H -плоскостной РА (рис. 1) с прямоугольными возбуждающими волноводами. Для таких прямоугольных РА с плавным изменением размеров основной особенностью является возможность строгого определения внешнего возбуждающего поля, соответствующего волне Н 10 прямоугольного волновода. В секториальной E -плоскостной РА расширение рупора происходит в плоскости вектора E . Для такой антенны удобно использовать цилиндрическую систему координат, так как фазовый фронт волны в раскрыве РА образует часть поверхности цилиндра, ось которого проходит через точку O .

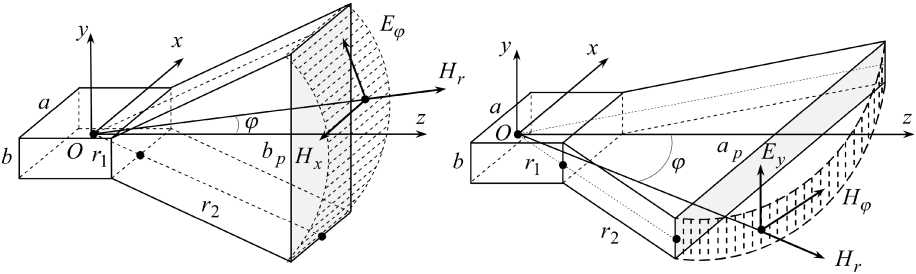
Рис. 1. Секториальные E - и H -плоскостные рупорные антенны

Тогда волновое уравнение для составляющей Е^ с учетом граничных условий принимает следующий вид [4]:

д 2 Е^ 1 d Е   д ² Е^ (

+ -^ +     + 1 к

д r2   r дr    дx1 V

—

r

Е „ = 0,

где к = ю^гaцa ; го - циклическая частота электромагнитного поля; sa, цa - абсолютные диэлек- трическая и магнитная проницаемости среды. Классический метод разделения переменных приводит к следующему решению [1]:

ЕФ = A Г H2 \y r) + PH? (yr)

nx cos ; a

H r = iA ——Г H ² ) ( y r ) + pH¹ ( y r ) ! sin—;

юц0a L                    J a

Hx = — iA—Г H02) (yr ) + pH01) (yr )1cos ^x, юц0 L                    J a где y = к\1 — (V2a)2 ; X - длина волны электромагнитного поля; a - размер широкой стенки возбуждающего волновода; A – амплитудный коэффициент, определяемый возбуждающим полем; первые слагаемые в квадратных скобках соответствуют падающей волне, распространяющейся в направлении положительных значений z , вторые слагаемые соответствуют отраженной волне, распространяющейся в направлении отрицательных значений z ; p – комплексный коэф- фициент отражения от раскрыва РА. Отметим, что для РА обычно |р| < 0,2, что приводит к не- значительному уменьшению мощности излучения РА, что легко учесть в программном комплексе ММ антенны, при этом общая структура поля в раскрыве не изменяется. Без ограничения общности в дальнейшем будем считать p = 0.

В секториальной H -плоскостной РА (см. рис. 1) расширение рупора происходит в плоскости вектора H . Волновое уравнение для составляющей Ey с учетом поля возбуждения в цилин- дрической системе координат записывается следующим образом [1]:

д ² E   1 д E   д ² E

= 0.

—+--- + + k 2 E дr2   r дr    дф2

Решение этого волнового уравнения также получают методом разделения переменных:

E - = B ^{[ Н}П ^{2 )}( ^kr ) + pH ?⁾( ^kr ) 1 cos т^Пф-;

L2

Hr = -i— [H2 (kr) + pH (kr )1 sin   ;(4)

юцдr L                    J

H ф=- iikB- [ H n ²’' ( kr ) + pH * "' ( kr ) ] ^cos 5т •

®Цо l                     ^   2фо где штрих означает дифференцирование по аргументу kr ; n = п/2фо , 2фо - полный угол раствора рупора; B – амплитудный коэффициент, определяемый полем возбуждения. Из соотношений (2), (4) следует, что волны как в E-плоскостной, так и в H-плоскостной РА могут рассматриваться как волны линейного источника, расположенного на расстоянии r1 от начала рупора. Кроме того в реальной РА возникают волны высших типов в месте перехода от волновода к рупору, а также у раскрыва рупора. С помощью этих волн можно полностью удовлетворить граничным условиям в зонах сингулярности РА, однако высшие типы волн быстро затухают при распространении, поэтому их влияние приводит к уменьшению мощности излучения РА без изменения общей структуры поля в раскрыве, определяемой соотношениями (2), (4).

Электромагнитное поле излучения пирамидальной РА представляет собой комбинацию полей секториальных E -плоскостной РА в плоскости вектора E и H -плоскостной РА в плоскости вектора H [1, 2]. Экспериментальные исследования амплитудно-фазового распределения (АФР) поля в раскрыве РА, анализ соответствия теоретических расчетов диаграмм направленности (ДН) РА и результатов измерения ДН для антенн различной конфигурации подтверждают правильность концепции комбинации полей излучения секториальных антенн. Подчеркнем, что принципиально важным для такого подхода является выбор амплитудных коэффициентов A , B в выражениях (2), (4), обеспечивающий баланс мощностей излучения секториальных антенн. Для выбора этих коэффициентов предлагается следующий метод.

• 1.    Введем эквивалентные электрические и магнитные токи в раскрыве секториальных антенн, исходя из структуры электромагнитных полей (2), (4): для E- плоскостной РА: j^e_x = - H_y ; j - = H_x ; j m = E_y ; для H -плоскостной РА: j - = H_x ; j ^” = E_y , так как вектор нормали й

• 2.    Определим мощность излучения РА следующим образом:

• 3.    Проведем дискретизацию поверхности S_a на одинаковые прямоугольные конечные элементы. Для достижения приемлемых точностей моделирования электромагнитных полей достаточно выбрать наименьший размер стороны элемента d min <Х/ 16 [5]. Для численного интегрирования выражения (5) будем использовать квадратурные формулы Гаусса – Лежандра с числом узлов 16–24. Применение высокоэффективного программного комплекса позволяет оперативно получать результаты моделирования с относительной погрешностью порядка 10 - 9 .

• 4.    Использование условия баланса подводимой мощности от внешнего генератора и излучаемой мощности позволяет определить амплитудные коэффициенты A , B для секториаль-ных РА. Такой баланс необходим для обеспечения равенства энергетических характеристик при расчете электромагнитных полей отдельно для E- плоскостной РА и H -плоскостной РА, так как для них используются разные ММ. Отметим, что расчеты ДН РА не требуют такого баланса амплитудных коэффициентов A , B , так как в результате вычислений получают только нормированные зависимости. В результате рационального выбора амплитудных коэффициентов A , B можно получать распределения плотности потока мощности излучения в произвольной плоскости для произвольного угла наблюдения. Рассмотрим основные этапы метода выбора коэффициентов A , B .

• 4.1.    По соотношениям (2), (4) производится расчет распределений эквивалентных токов в апертуре секториальных РА. Эти распределения трансформируются для апертуры пирамидальной РА с помощью стандартных численных процедур геометрического подобия.

• 4.2.    По известным распределениям эквивалентных токов в апертуре РА можно рассчитать значения составляющих векторов E , H поля излучения в произвольной точке наблюдения с координатами ( x , y , z ) по следующим строгим выражениям [6]:

к поверхности раскрыва S_a имеет только одну z -составляющую.

P ^ = Re j П • Й ds ,

Sa где П = 0,5E х H* - комплексный вектор Пойнтинга, определяемый из строгих электродинамических соотношений. В качестве поверхности интегрирования выберем апертуру Sa пирамидальной рупорной антенны. Такой выбор широко используется в методе физической оптики, и в первую очередь обусловлен предположением отсутствия затекания токов проводимости на внешнюю «теневую» поверхность антенны. Это предположение выполняется тем точнее, чем выше удельная проводимость материала стенок рупора и качество технологии изготовления. Тогда замкнутую поверхность, охватывающую РА, можно заменить конечной поверхностью Sa , что значительно упрощает анализ поля излучения без заметного ухудшения качества математического моделирования РА.

Ex = I j^rA ds'; Hx = л \7 J Г"jm (Fr + rx2Dr ) + ikZcjeerzBr 1 ds'; 4nik •                       4nikZ_ ' L \           iJ

Sa

E y =         j^e e ( F r + r y D r ) + чМг ds '; H y =   ' J J' xm r y² D r ds ‘ ;

4 n ik*     ^x           ’  Z„                 ⁷   4 n ikZ„ ;

Sa                          cc

E z

Z c

4 n ik

I" j ^er r D

J Jy'z'y^r

—

ik m jx ry r Zc

ds'; Hz = A 7 7 J [jmryrzDr — ikZcj'erxBr1 ds', 4nikZ„ * L                        J c Sa

где r _x = x — x '; r _y = y — y '; r z = z — z' , штрих означает принадлежность к координатам точки ис-

7 I /                                                                      — 1 — ikr + к ² r²

точника; Zc =л/ц a pa a - волновое сопротивление среды; функции Fr =------- r2

• 3    + 3ikr — к2 r2         1 + ikr        exp (—ikr)„

Dr =-----------ф; Br =—-—ф; ф =-------- . С помощью выражений (6) можно рассчитать r4                   r2

распределение вектора Пойнтинга в заданных точках, следовательно, можно получить детальную информацию о плотности потока мощности излучения РА. На рис. 2 приведен график распределения плотности потока мощности на осевой линии в ближней зоне РА со следующими характеристиками: ap =0,115 м; bp =0,105 м; a =0,053 м; b =0,030 м; r1 + r2 = 0,113 м для E-плос костной РА; Tj + r- =0,155 м для H-плоскостной РА; расчеты производились на частоте 4,7 ГГц. Отчетливо выделяется область реактивного ближнего поля, где помимо продольной компоненты вектора Пойнтинга существуют и поперечные компоненты. Монотонный участок распределения удобен для построения экспериментов, где особую важность имеет прогнозируемый уровень плотности потока мощности.

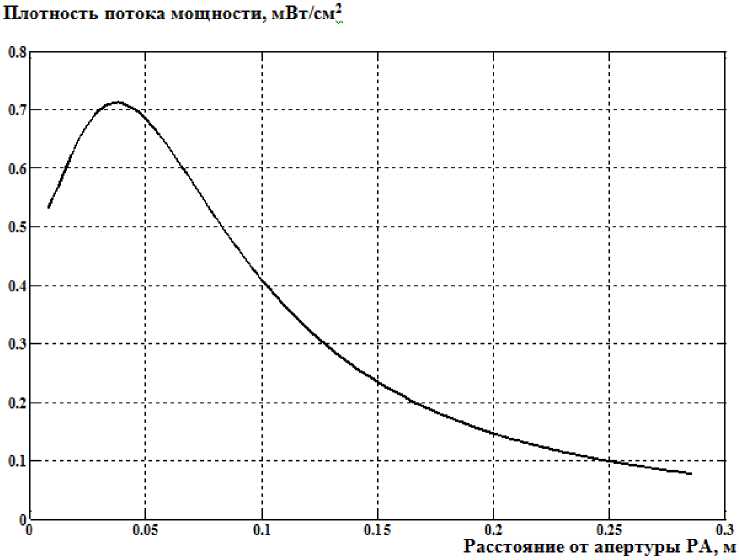
Рис. 2. Распределение плотности потока мощности излучения РА

Выводы

• 1.    Применение строгих электродинамических соотношений для построения ММ пирамидальной РА позволяет с высокой точностью рассчитать требуемые энергетические характеристики ближнего поля, где проводятся основные эксперименты для изучения взаимодействия биологических объектов с электромагнитным полем. Применение известных методов расчета поля излучения РА с использованием асимптотических приближений дальней зоны не дает гарантированных оценок энергетических характеристик поля излучения в ближней зоне.

• 2.    Полученные результаты моделирования поля излучения в ближней зоне показывают высокую эффективность и универсальность предложенных ММ.

• 3.    Характерной особенностью предложенного метода аппроксимации АФР поля в раскрыве РА является необходимость тщательного выбора коэффициентов A , B для баланса энергетических характеристик E- плоскостной и H -плоскостной РА. Существенного ускорения моделирования можно добиться при использовании высокоэффективного программного комплекса численного интегрирования методом Гаусса – Лежандра.