Математическая модель оценки рисков в процессе выбора исполнителя технологической операции на производстве

стемы [1]. В своей деятельности предприятия с целью снижения рисков, должны применять в работериск-ориентированный подход, который основывается на принятии решений и использовании программных средств [2, 3]. Предприятие, исходя из стандарта ISO 9001:2015 должно проводить оценку рисков посредством анализа, подбора воздействия и оценки результата воздействия. С практической точки зрения процесс принятия решений требует апробации на аналогах – моделях т.к. апробация на реальных объектах не всегда экономически целесообразна. Статистические и математические методы оценки рисков на современных производственных предприятиях используются не в полном объеме. В основном аналитикой рисков занимаются финансовые организации [4]. Особенно важно оценивать риски в процессе изготовления изделий, в которых не учитываются потери по времени, где возможны большие финансовые потери [5]. Рассмотрим статистический подход для определения количественных оценок на примере управления рисками процесса выбора исполнителя технологической операции на многономенклатурном производстве.

ОПИСАНИЕ ЗАДАЧИ

Процесс производства начинается с планирования и формирования перечня производственных задач, которые достигаются за обозримый период. Задачи разбиваются на технологические операции. Каждая технологическая операция выполняется на рабочем центре

(РЦ). Выбор в пользу того или иного РЦ не всегда может быть адекватным. Для автоматического-управления процессом определения передачи задания на рабочий центр необходимо понимание внутренних и внешних факторов, влияющих на выбор исполнителя с учетом негативных последствий.

Нетривиальность решения поставленной задачи определяется:

• -    сложностью процесса изготовления, структуры производства, учетом большого количества параметров;

• -    многообразным воздействием внутренних и внешних факторов;

• -    невозможностью использования математической статистики и моделей процесса функционирования.

Таким образом, необходимо комплексное решение проблемы минимизации рисков, где основными этапами являются: идентификация рисков; анализ рисков; минимизация рисков и мониторинг [2-3].

МЕТОДИКА ОЦЕНКИ ЭФФЕКТИВНОСТИ

Управление рисками – сложный и динамический процесс, который характеризуется множеством возмущающих факторов, имеющий как предсказуемый, так и случайный характер возникновения [4, 5]. Аналитический метод и метод статических испытаний – методы, которые обеспечивают оценку вероятностных событий, однако аналитический метод более трудоемкий и требует большие вычислительные ресурсы ПЭВМ. На предприятиях с большим массивом данных технологических операций использование метода статистических испытаний оправдано. Метод позволяет оценить значения средних (минимальных и максимальных) ожидаемых значений результатов и их отклонений.В работе используется имитационное моделирование процесса выдачи заданий в производство [6,7], производится многократный опыт с моделью, в которой реализованы пошаговые алгоритмы поиска показателя риска.

Пусть необходимо минимизировать риск невыполнения технологической операции на механообрабатывающем производстве. Критерий минимизации риска обозначим K _min r . Критерий K _min r является функцией изначально заданных условий U ⁽⁰⁾ , формируемых на этапе планирования. K _min r зависит от множества факторов технического характера М ф2 _х и индивидуальных факторов исполнителя М ф^ . K _{min r} является функцией экономических потерь ф . Представим факторы риска в виде следующего множества:

• м » -МО Х • M isi ) , (1) где М ф2 _х — множество факторов технического характера, влияющих на оценку риска; М^ -множество индивидуальных характеристик, влияющих на оценку риска.

Критерий K _{min r} , определяющий минимальный риск представим в виде функции:

K mm r = f 'U^' , M^s* , ф ) . (2)

Сущность метода состоит проведении N испытаний в результате которых получают N возможных значений X. Производится вычисление среднего арифметического значения и принимают полученное значение в качестве приближенного значения искомого числа. Общий алгоритм метода в поставленной задаче представлена на рис. 2. Практическая реализация алгоритма построена на основе автоматизированной системы учета технологических данных, в которой производится регистрация всех отметок выполнения технологических операций (ТО). Моделирование процесса производится с ограниченным количеством критериев. Процесс моделирования заключается в получении изначальных заданных целевых показателей и

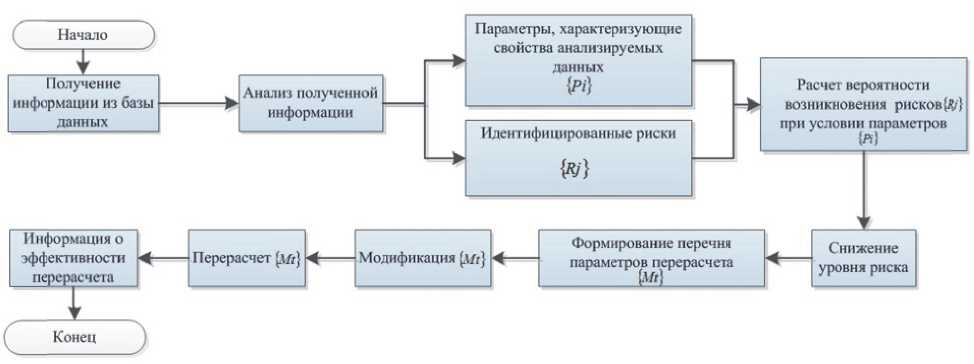
Рис. 1. Схема управления рисками выбора исполнителя

выработке значений по управлению заданными

ходимо просчитать число выполняемых итера-

параметрами.

ций, которое можно вычислить по выражению:

. Д[к]Т n - ^^' еи

начальные условия принимают значения слу-

чайных величин полученных на A Ti , где U (0) должен отвечать f ( и ^<0)).

Проведя n-итераций, получим статистический набор величин, которые обработаем ис-

Используя теорему Бернулли [8,9] получаем, что К_ср = m/n, где m – количество успешных испытаний, n – общее количество испытаний. Если М[К ср ]= р ;

Р- g

Д[ К_ср ]= _n , тогда

J m ...

P 1— < e>> I n I

^ q - ^ lim P n ' e      n ^"

m

— Р

n

< e

= 1.

пользуя математические методы статистики [8].

Среднее значение рассчитывается по следующей формуле:

КСР

nK

Z—i j = 1 j

s

n

Получаем количественную оценку риска невыполнения задачи. Эффективность принимаемых решений полученных от сравнительной оценки показателей эффективности рассчитываются по следующей формуле:

где n – количество итераций.

При большом числе реализаций n случайной

A P =

К min pj

К min pi

к min pi

величины вероятность того, что величина отклонений среднего математического ожидания от математического меньше любого положительного числа e стремится к значению «1»:

lim P { ^_ср - М [ K ] } < е = 1 . n ^ю ^И           I

Из полученного выражения получаем, что к _ср « м [ к ] . Оценку дисперсии Д[К] случайной величины определяем по формуле:

Д [ к ] = ¹ X n ( K i - K , ) ’ . n

Для приведения оценки Кср к значению, близкому к математическому ожиданию М[К], необ- где К – значения сравнительных показателей эффективности.

Для оптимального принятия решения необходимо так же учитывать затраченное на расчеты время, экономическую составляющую и значения ограничений.

ОЦЕНКА РИСКА НА ПРИМЕРЕ ВЫДАЧИ ОПЕРАЦИИ В МЕХАНООБРАБАТЫВАЮЩЕЕ ПРОИЗВОДСТВО

В качестве примера необходимо распределить заготовительные операции по РЦ. В ка-

Уровень выполняемой

ТО ____

Доступность РЦ

Выявление данных технического характера

Уровень приоритета

Определение параметров

■> Уровень конкуренции

^ Сроки изготовления

Имитация процесса

Получение массива данных

Выявление экономических характеристик

Анализ результатов

Выявлснис индивидуальных характеристик

Уровень брака

Уровень производительности Специфика производительности

Оценка эффективности

Рис. 2. Алгоритм действий имитационной модели

Таблица. Классификация индексов

Значение индекса качества Описание классификации риска 1 риск отсутствует - в случае, когда отсутствуют факторы, исключающие невыполнение ТО за срок, установленный в ТО 0,90-0,99 допустимое значение риска - в случае, когда существуют факторы, влияющие на процесс, но исключающие невыполнение ТО 0,75-0,89 риск средний - в случае, когда один или несколько исполнителей выполняют ТО со значительным срывом. 0,6-0,74 критическое значение риска, при котором исполнитель либо чрезмерно загружен, либо в очереди его задач находятся задачи, сильно зависящие от внешних, независящих от исполнителя факторов (поставка материала точно к сроку). Ниже 0,6 риск недопустимый, исполнитель исключается, т.к. задача является заведомо невыполнимой честве критерия индекса качества определена классификация в соответствии с таблицей.

Весь перечень задач (рис. 3) распределяется по типу номенклатуры (прокладка, стенка и т.п.) и по каждому типу из базы ТО определяется потенциальный исполнитель – просматривается в хронологическом порядке история выполнения ТО.

На каждый объект номенклатуры формируются средние значения начальных параметров К_ср . На рис. 4 отражена выборка показателей номенклатуры «Ловерс У-01-01». Из выбранного набора определяется набор параметров, ограничением значений в соответствии с критериями индекса и рассчитывается приращение ∆ P .

ЗАКЛЮЧЕНИЕ

Предлагаемая модель трудоемка в реализации и требует большого объема информационных данных. На практике данная модель оправдала себя в том числе при критических рисках. Модель позволяет получить оценку целесообразности сделанного выбора и оценить её эффективность.

Дальнейшее развитие описанной модели заключается в использовании неограниченного числа внешних факторов, что позволит более точно учесть специфические особенности объекта и более точно определить РЦ для выполняемой технологической операции.

^ Таблица *                                                                                                       о || 0 I k^Hj

№п/п	н 0) 1X а о X С	с О 2 й	Наименование работ	дц	о 00 0) У	X X г я Ф о 3	X го а> О	S ф о Н	>Х Ф X СИ Ч z 2 о с о о	о ох н 5 S ф Sogo X О $ 9 О ° о Ч g S	Изделие	Kmin
1	с	1001.17	Наконечник ПГ18 ОСТ5 6070-74	АБ В-100	1	5	Заготовительная	0 004	539885-10 11.16, 666699 03 10.16	ПО6-15-00133	Изделие 1	0,11
2	с	10.01 17	Наконечник ПГ18 ОСТ5 6070-74	МДВ-202	1	10	Слесарная	0 008	539885 10 11 15. 666699-03 10.16	П06-15-00133	Изделие 1	0.27
3	с	16.03 17	Люверс	У-01-О1	16	5	Заготовительная	0 08	474299 09 12 14	П06-14-ОО536	Изделие 106	0.16
4	с	16 03 17	Люверс	AM3-300	16	10	Слесарная	0.272	474299 09.12 14	Г106 14 00536	Изделие 106	0.90
5	с	16.03.17	Люверс		16	20	Штамповочная	0.0528	474299-09 12 14	П06-14-ОО536	Изделие 106	0.90
6	с	16.03 17	Люверс		16	50	Штамповочная	0.0528	474299-09.12.14	П06-14-0О536	Изделие 106	0.89
7	с	28.03 17	Ловитель		8	5	Заготовительная	0.136 568740-10.06.16		П06-15-0М03	Изделие 707	0 09
8	с	28.03 17	Ловитель		8	10	Слесарная	0.0664	568740-10.06.16	П06-15-0О403	Изделие 707	1
9	с	28 03 17	Винт		2	5	Заготовительная	0 097		П06-15-0О403	Изделие 707	0.01
10	с	28 03 17	Винт		2	10	Слесарная	0 004		П06-15-00403	Изделие 707	1
11	с	03 04.17	Стенка		1	10	Слесарная	015	674817-08 12 16	П06-16 00299	Изделие 2	1
12	с	03 04 17	Прокладка		2	5	Заготовительная	0 295	574490	П06 15 00440	ИИ	0.24
13	с	03 04.17	Прокладка		2	10	Слесарная	0.0172	574490	П06 15 00440	ИИ	0.41
14	с	03 04 17	Шайба 2,5x6,5x0,5 СТЭФ-1	ГОСТ	8	10	Слесарная	0 533	674612 06 02 17. 732121-04 04.17	П06-16-00330	251	0.06
15	с	03 04.17	Шайба 2,5х6.5хО.5.СТЭФ-1.		8	5	Заготовительная	0.219	674612-06 02.17. 732121-04 04.17	П06-1640330	251	0,62
16	с	03 04 17	Шайба 2.5х6.5х0.5 СТЭФ-1		8	10	Слесарная	0 533	674710-06 02.17. 732120-04 04.17	П06-16-00295	251	0.08

*                                                                                                                       111____________________________________ ►

Рис. 3. Перечень задач ТО

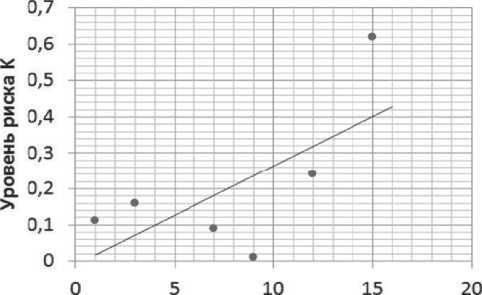
Значение показателя

Рис. 4. График итераций на «Ловерс У-01-01»