Математическая модель одномерного пространственного сканера для распределенной системы обработки информации
Бесплатный доступ
В данной статье рассматривается математический аппарат построения пространственного сканера для распределенной системы обработки информации. Пространственные сканеры позволяют обнаруживать пространственно-модулированные сигналы в распределенном входном воздействии. Они также применяются для настройки параметров пространственных фильтров, которые необходимы для выделения из распределенного входного воздействия заданных пространственных мод (магистралей). Пространственные сканеры и пространственные фильтры в совокупности образуют блок обработки распределенного сигнала.
Математическая модель, входное воздействие, граничные условия, коэффициент передачи, система с распределенными параметрами, распределенный сигнал, пространственный сканер
Короткий адрес: https://sciup.org/140287830
IDR: 140287830 | УДК: 519.711.3
Текст научной статьи Математическая модель одномерного пространственного сканера для распределенной системы обработки информации
Положим, что имеется распределенный объект, схема которого указана на рис. 1.
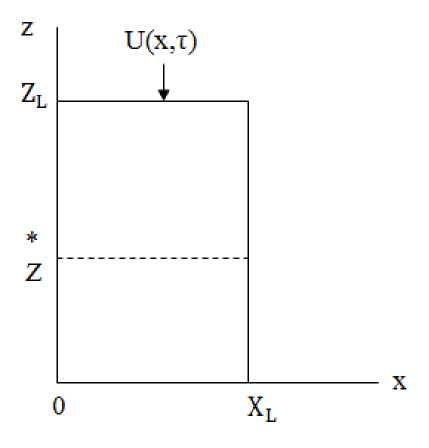
Рис. 1. Схема распределенного объекта
Математическую модель представленного выше объекта можно описать следующим уравнением:
d2T(x,z, т ) d2 T(x ,z ,т )
А-----+ T(x, z, т) + ---—3---= 0,
dx 2 dz2
(0 где А - заданное число, х, z - пространственные координаты, т - время, Т (х,z,т) - фазовая переменная, Xl, ZL- заданные величины. Граничные условия, помимо входного воздействия, будем считать нулевыми. Они будут представлены в виде следующих соотношений: T(x = 0,z,t) = T(x = Xl,z,t) = 0, dT(x, z = Zl,t) dz = U(x,t), dT(x, z = 0,t) _ dz Положим, что входное воздействие представлено в виде ряда Фурье по пространственной координате, которое, с учётом граничного условия T(x = 0, z, т) = T(x = Xl, z, t) = 0, записывается в виде: U(x,T)= ZiiiW-sinCTfx), ф. = я'^ где Cj(t) - заданные функции (т. е. функции, несущие информацию о полезном сигнале). Требуется определить T(x,z = 2^,т), где Z - заданное число (0 Реакция объекта на каждую моду входного воздействия следует определять в виде: Ti(x,z,T) = Hi(z,i) • sin^ ■ x), где Hi(z,T) - определяемые функции. Подставляя выражение Ti(x,z,T) = Hi(z,t) • sin^ ■ x) в уравнение математической модели рассматриваемого распределенного объекта и преобразуя, получим следующее: - Л^Л Hi(z,T) + Hi(z,T) + d2Hi(ZT)= 0, или д2^т)+ (1 - Л-Vj2) • Hi(z,T) = 0 Функцию Hf(z,T) следует искать в виде: Hi(z,T) = Bi,i • ee •' ■ B24• e eiz, где ei = (A • 'ч — 1)1/2, B1,i, B2,i - функции, определяемые из граничных условий. Подставив Hi(z,T) = B1,i • eei'z+ B2,i • e-ei'z в формулу реакции объекта на моды входного воздействия Ti(x,z,t) = Hi(z,t) • sin^ • x) и далее ∂T(x,z=0,τ) в---—---= 0, придём к следующему соотношению: B1,i • Pi - B2,i • Pi = 0, или Bi,i = В2Д . Подставив Hi(z,T) = B1,i • eei'z+ B2,i • e-ei'z в формулу реакции объекта на моды входного воздействия Ti(x,z,t) = Hi(z,t) • sin^ • x) и далее ∂T(x,z=Z ,τ) в---------= U(x, т) = 0, получим: ∂z Bi,i • Pi • (eerZL- e- e'ZL) = C/t) Значение B1,i определяется из следующего соотношения: ̅C̅̅i(τ) 1,i Pi^rZL- e- eTZL) Реакцию объекта на каждую моду входного воздействия можно записать в виде: ̅̅̅ β ∙Ż - β ∙Ż Ti(x, 2,т) = c^l- Д^) • Sin(Vi • x) Функция выхода рассматриваемого объекта определяется из следующего соотношения: ̅C̅̅i(τ)∙ (eβi∙Ż- e- βi∙Ż) Ti(x, 2,т) = 2i=i ei(e₽i’zL- e- erzL) ^ sin(^i - x) Коэффициент передачи (Kt = Ti(x, 2^,т)/ (C,(t) • sin(Vi • x))) по каждой пространственной моде определяется из следующего соотношения: eβi∙Ż - e- βi∙Ż Ki = ei • (ePrZL- e-PrZL) ’ 1 = 1,го, где ei = (A • ^12 — 1)1/2. Положим, что A = 1/G, где G является непрерывной функцией, пробегающей все значения Ф2, 1 = 1, го (эту функцию называют обобщенной координатой). Для значений G ^ Ф2, (1 = 1, го) ei ^ 0, а значение abs(Ki) ^ го. Уравнения А • —T^z-) + T(x, z, т) + ^-Txz-) = 0, (0 XL), T(x = 0, z, t) = T(x = XL, z, t) = 0, dT описывают модель одномерного пространственного сканера, коэффициент передачи по каждой пространственной моде которого определяется из соотношения eβi∙Ż - e- βi∙Ż Ki = et • (eefZL- e- efZL) , 1 = 1, го, где в1 = (A • ^12 - 1)1/2. Если входное воздействие представлена в виде U(x,t)= Zi=1 Ci(T) • sin(^i • x), то изменяя значении A от 0 до го, могут быть определены пространственные частоты ^12 пространственных мод, формирующих входное воздействие U(x,t).
Список литературы Математическая модель одномерного пространственного сканера для распределенной системы обработки информации
- Першин И.М. Синтез систем с распределенными параметрами. - Пятигорск: Изд-во "РИО КМВ", 2002. - 212 с.
- Першин И.М. Синтез систем с распределенными параметрами // Мехатроника, автоматизация, управление. 2005. №6.
- Першин И.М. Распределенная система передачи информации // Мехатроника, автоматизация, управление. 2005. №11.
- Першин И.М. Распределенная система передачи информации // Управление и информационные технологии. Межвузовский научный сборник. Пятигорск, "РИА-КМВ". 2007. С. 43-57.
- Першин И.М. Система обработки распределенных сигналов // Труды VIII международной научно-технической конференции по динамике технологических систем. Том 1. Ростов-на-Дону. 2007. С. 196-202.
- Першин И.М. Распределенные системы обработки информации. Пятигорск, "РИА-КМВ". 2008. - 148 с.


