Математическая модель определения продажной цены продукции, гарантирующей безубыточность основного вида деятельности промышленного предприятия с заданной вероятностью

Внедрение прогнозно-адаптивного подхода и математической модели управления промышленным предприятием в условиях неопределенности [1] в ОАО «Кузнецкие ферросплавы» показала, что для определения продажной цены продукции, гарантирующей безубыточность основного вида деятельности промышленного предприятия с заданной вероятностью, целесообразно использовать математическую модель, представленную в данной статье.

Постановка и математическая модель задачи

Условия задачи:

• 1)    в качестве вида деятельности рассматривается производство одного (основного) вида продукции (для ферросплавных производств основным видом продукции является производство ферросилиция);

• 2)    данный вид продукции производится многими предприятиями и ни одно из них не занимает доминирующее положение на рынке;

• 3)    спрос на данный вид продукции является неэластичным по цене;

• 4)    суммарные производственные мощности всех предприятий при полной загрузке смогут покрыть любые запросы всех потребителей.

Поскольку спрос на продукцию не зависит от ее цены, в дальнейшем будем рассматривать две независимые случайные величины:

C – средняя себестоимость единицы продукции;

S – суммарный объем потребления продукции в год.

Объем продаж продукции рассматриваемого предприятия в зависимости от совокупного спроса S обозначим, как f(S). Это может быть любая зависимость, найденная на основании исто- рических данных, с учетом технологических ограничений и т. п. В простейшем случае это некоторая логистическая функция, которая сверху ограничена некоторым значением, равным максимальному объему выпуска основного вида продукции предприятия. Пример графика подобной функции представлен на рис. 1.

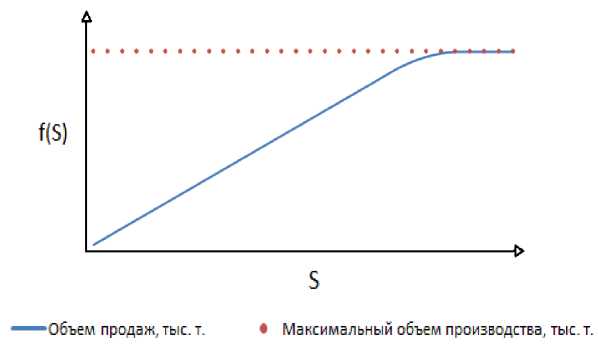
Рис. 1

Целью задачи является нахождение некоторой фиксированной продажной цены продукции в рамках конкретного контракта, гарантирующей безубыточность одного (основного) вида деятельности промышленного предприятия с заданной вероятностью.

Поскольку аналитическую модель для такой задачи построить практически невозможно (присутствуют стохастические переменные, имеется необходимость оценки многих параметров во времени), построим имитационную модель и найдем решение с помощью многократного проведения численного эксперимента.

Предположим, что изменения цен, объемов продаж и периода времени дискретны (что вполне допустимо, поскольку частота дискретизации может быть достаточно мала).

Введем обозначения:

N – множество возможных значений цен;

M – множество возможных значений совокупного спроса на продукцию, за единицу времени;

• Y    – размер временного интервала, на который производится расчет задачи;

C ij – цена на продукцию (в рублях), соответствующую варианту i , в единицу времени j , i e NJ e Y;

P_i j – вероятность того, что в единицу времени j цена примет значение, соответствующее ва-рианту i,i e N,j e Y;

V ij – спрос на продукцию (в единицах продукции), соответствующий варианту i , за единицу времени j , i e M,j e Y;

O ij – вероятность того, что в единицу времени j спрос примет значение, соответствующее варианту i , i e M,j e Y;

A j - постоянные затраты (в рублях) за единицу времени j , j eY;

B j – объем производства (в единицах продукции), который планируется зафиксировать в качестве минимального в контракте, за единицу времени j , j e Y;

• β    – требуемая частота случаев, при которой совокупные доходы будут не ниже совокупных расходов;

• γ    – зафиксированная цена в контракте;

• Z    – количество итераций расчета;

D – количество итераций, в которых совокупные доходы были выше совокупных расходов.

Предварительной задачей для моделирования является расчет значений P ij , C ij , V ij , O ij , i e N,j e Y, то есть необходимо осуществить прогнозирование временных рядов. Для этого можно использовать множество подходов. Для примера отметим два следующих, каждый из которых обладает своими преимуществами и недостатками.

Математическая модель определения продажной цены продукции, гарантирующей безубыточность основного вида деятельности…

Первый . Прогнозирование на основе эконометрических моделей [2].

Преимущества прогнозирования на основе эконометрических моделей:

• –    объективность полученных прогнозов и оценки качества полученных моделей;

• –    возможность математического поиска факторов (в том числе и тех, которые оказывают неявное влияние), воздействующих на результирующую переменную;

• –    имеется широкий спектр моделей, позволяющий подобрать наиболее подходящую в зависимости от условий задачи.

Недостатки эконометрических моделей:

• –    ориентация на исторические данные, что при каких-либо качественных изменениях факторов, влияющих на результирующую переменную, снижает качество модели;

• –    высокие требования к качеству и количеству исходных данных;

• –    высокие требования к уровню квалификации специалистов, осуществляющих эконометри-

• ческое моделирование.

В качестве эконометрических моделей можно, например, использовать:

• 1.    Авторегрессионную модель ( AR ( p )) [2]:

• 2.    Модель авторегрессии – скользящего среднего ( ARMA ( p , q )) [2]:

^X t = ^С + E^ « i • ^X t-i + £ j .

^ t = ^С + E^ « i • ^X t-i + E^ P i • E t-j + ^E i ^.

Второй . Прогнозирование на основе экспертных оценок [3]:

Преимущества данного подхода:

• •    во многих случаях пользователь не обладает достаточной или достоверной статистической информацией, необходимой для математических методов расчета прогноза;

• •    возможен учет влияния факторов, которое невозможно определить на основании историче-

• ских данных.

Недостатки:

• •    возможен субъективизм как при получении прогнозов, так и при оценке качества полученных моделей;

• •    необходимость хорошего знания экспертом предметной области;

• •    существует вероятность упустить влияние факторов, которые, на первый взгляд, не оказывают воздействие на результирующую переменную.

При выборе оптимального подхода для прогнозирования временных рядов следует учитывать их преимущества и недостатки. Также отметим, что при прогнозировании временных рядов возможно комбинирование различных подходов, что позволяет в некоторых случаях использо- вать преимущества и нивелировать недостатки нескольких подходов.

Таким образом, задача сводится к нахождению такого значения γ, при котором будет выполнено ограничение на β, то есть количество случаев, при котором совокупные доходы будут не ниже совокупных расходов. Для этого многократно сгенерируем возможные ситуации с задан- ными вероятностями и подсчитаем, сколько раз выполняется ограничение.

Обозначим L ym – объем продукции, который мы сможем продать сверх заложенного по контракту, в период времени y, если спрос будет соответствовать номеру m :

= f/(^ m(y)y )  ^B y '/(^ m(y)y ) — ^B y

I      °'^⁽^ m(y)y ⁾ >  ^B y

—

L ym(y)

.

Совокупные доходы (при вариантах цен n ( y ) и значениях спроса m ( y ), за все периоды времени Y ):

I z = Е уек У • B_y + C_yn (y) • L_ym (y) .

Совокупные расходы:

O z   ^Z ygy (^C_n (y)y (^B y + L y _m (y)^ + A y ).

Алгоритм расчета задачи представлен в виде блок-схемы (рис. 2), в которой Генерация_С(y) – функция, которая возвращает прогноз издержек на момент времени y; Генерация_V(y) – функ- ция, которая возвращает прогноз спроса на момент времени y.

В результате многократного использования алгоритма для различных заданных вероятностей на модельных данных можно получить таблицу соответствия между контрактной ценой на продукцию и вероятностью, с которой данная цена позволит осуществлять безубыточную деятельность предприятия. Графически данная зависимость, рассчитанная на модельных данных, представлена на рис. 3.

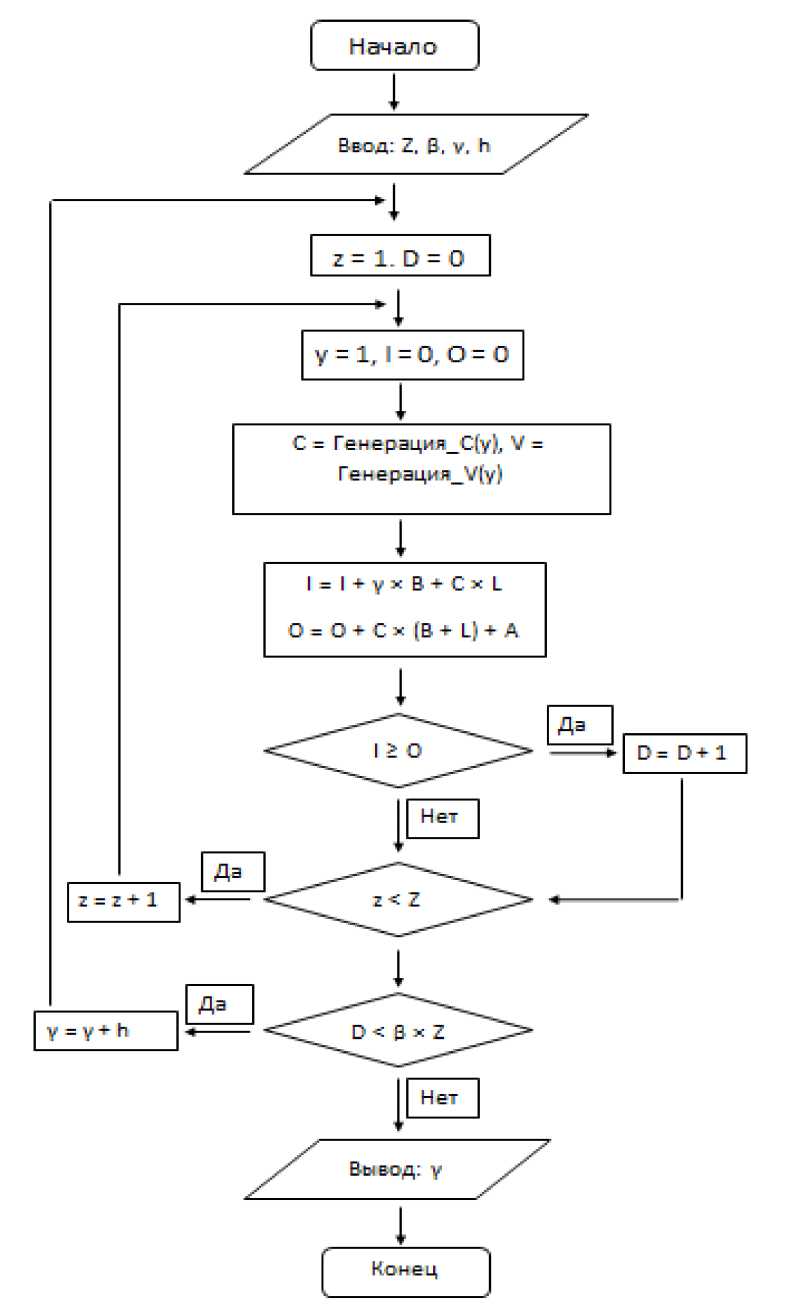
Рис. 2

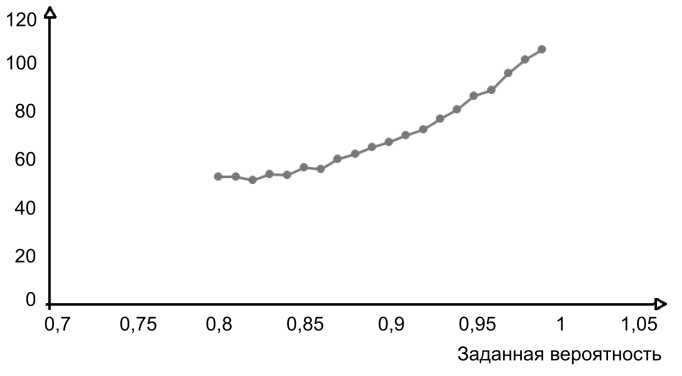
Рис. 3

Математическая модель определения продажной цены продукции, гарантирующей безубыточность основного вида деятельности…

Заключение

Представленная математическая модель позволяет аналитикам промышленного предприятия расчитывать продажные цены на основной вид продукции предприятия с гарантией безубыточности.