Математическая модель оптимального распределения ресурсов в строительной сфере в условиях их дефицита

Материально-техническое обеспечение в сфере строительства является одной из важнейших ее составляющих, непосредственным образом влияющих на успешность реализации строительных проектов. Несвоевременная поставка необходимых для строительства ресурсов приводит к незапланированному увеличению сроков выполнения строительных проектов, увеличению сметных стоимостей как отдельных работ, так и всего проекта, неравномерной загруженности необходимого оборудования, техники, транспортных средств и иным существенным последствиям [1, 2].

Таким образом, проблема оптимального распределения имеющихся ограниченных ресурсов является важной и актуальной задачей при планировании и организации строительных работ, особенно в условиях дефицита ресурсов. Решение этой задачи непосредственным образом влияет на качество и результат выполнения строительных проектов, продолжительность и ритмичность строительства, затраты и производительность труда [3, 4].

Под ресурсами в строительстве будем в дальнейшем понимать любые виды ресурсов, поставляемые на строительный объект и необходимые для выполнения строительного проекта: строительные материалы, конструкции и детали, человеческие ресурсы, запасные части, комплектующие, энергоресурсы, оборудование и прочие ресурсы [5].

Цели и задачи

Целью данной научной работы является разработка математической модели, основанной на методах векторной оптимизации, позволяющей оптимально распределять ограниченные по запасам ресурсы разного вида между строительными мероприятиями, работами или объектами с целью повышения эффективности выполнения строительных проектов.

Для решения поставленной цели необходимо решить следующие задачи:

– сформулировать и обосновать математическую модель распределения ограниченных ресурсов между строительными объектами, работами или мероприятиями;

– описать методику проведения вычислительных процедур для реализации модели в численном виде;

– на основе вычислительных экспериментов оценить эффективность применения модели распределения ресурсов при управлении строительными проектами.

Математическая модель оптимального распределения ресурсов

В данном разделе приведем математическую модель оптимального распределения ресурсов между строительными объектами и мероприятиями, которая отличается научной новизной. Она основана на теории оптимального управления на основе решения оптимизационных задач [6–9]. Данную модель можно одинаково эффективно использовать как для распределения ресурсов для выполнения строительных работ на нескольких строительных объектах, так и для распределения ресурсом между различными работами или мероприятиями по проведению строительства на одном строительном объекте.

Проблема заключается в том, что обычно ресурсы ограничены и, как правило, их количества не хватает для полноценного обеспечения всех строительных объектов. Но в условиях дефицита ресурса мероприятия по организации строительных работ на объектах строительства все равно осуществимы, так как необходимые ресурсы на такие мероприятия обычно планируются с некоторым запасом, который обеспечит идеальное его исполнение. В условиях дефицита ресурсов возможно выполнение мероприятий и с меньшим количеством ресурса, но эффективность мероприятия при этом может упасть на величину, не превышающую 20–30 %. Назовем минимальное количество ресурса, приводящего к выполнению мероприятий при проведении строительных работ, в рамках разумного падения его эффективности, достаточным количеством ресурса, отводимого на организацию строительных работ.

Приведем математическую постановку задачи оптимального распределения ресурсов между строительными объектами [8].

Пусть имеется n видов или типов некоторого ресурса, который обозначим как R 1 , R 2 , …, R n , его необходимо перераспределить на m строительных объектов с максимальным эффектом. Мероприятия или строительные объекты обозначим через M ₁, M ₂, …, M_m .

Введем следующие матрицы:

a ij , i = 1, 2, …, n ; j = 1, 2, …, m – необходимое количество ресурсов i -го типа, который должно получить j -й строительный объект (мероприятие) для проведении строительных работ при их идеальной реализации;

b ij , i = 1, 2, …, n ; j = 1, 2, …, m – достаточное количество ресурсов i -го типа, который должно получить j -й строительный объект или мероприятие для реализации строительных работ с минимально возможной эффективностью.

Также необходимо для построения адекватной модели распределения ресурсов учитывать важность строительных объектов или мероприятий [10]. Обозначим через W j , j = 1, 2, …, m – вес или важность j -го объекта или мероприятия по проведению строительных работ с точки зрения его вклада в решение комплексной задачи выполнения строительного проекта.

Кроме этого, для учета ограниченности ресурсов обозначим через Z i общий запас ресурсов i -го типа.

Необходимо определить х_i j – количество ресурсов i -го типа, которое должно получить j -е мероприятие или объект так, чтобы эффективность выполнения строительных проектов была максимальна.

Для решения этой задачи введем некоторый критерий эффективности [7] 8 j , который показывает, на какую долю уменьшится эффективность j -го мероприятия по проведению строительных работ, если ресурс i -го типа, распределяемый на него, в рамках допустимого значения уменьшить на единицу. Предполагая, что эффективность мероприятий по проведению строительных работ равномерно зависит от наличия ресурсов, из чего следует то, что падение эффективности мероприятия, связанное с нехваткой единицы ресурса, обратно пропорционально разности между достаточным и необходимым количеством ресурса [9]. Исходя из этого, критерий эффективности можно записать в виде

8 j =

a ij

^{- Ъ}У

i = 1,2,

■, n , j = 1, 2, — , m .

Критерием оптимизации F_i для нахождения оптимального распределения ресурса i -го типа будет служить целевая функция, которая имеет смысл обобщенной величины падения эффективности проведения строительных работ из-за недостатка необходимых ресурсов. Согласно [9] она должна быть мультипликативной от веса мероприятия W j , критерия эффективности 8 j , а также от количества ресурса, которого недостаточно на данное мероприятие: a ij – х ij . Согласно приведенным требованиям, целевая функция будет равна

F k ( X j ) = ^L ⁸ ij ( ^аУ ^- X j ) W j ^ min, ^k = 1,^2, — , n .                                             (2)

j = 1

Преобразовав алгебраически условие оптимизации (2) и изменив его направление, можно записать выражение, тождественное (2) с точки зрения оптимизационных задач:

F k ( x j ) = £ 8 ij W j X ij ^ max, k = 1,2, — , n , j = 1

а учитывая соотношение (1), можно записать

F k ( x « ) = t ^j ^ max, k = 1.2, — , n .

j = 1 a ij ^- b ij

Перейдем к ограничениям оптимизационной задачи. Как было сказано ранее, выделяемые на мероприятие по проведению строительных работ ресурсы не могут быть меньшими по величине, чем достаточные, но и не должны превышать необходимые. Если окажутся избыточные ресурсы, они будут направлены в общий резерв. Математически данные условия можно записать в виде

X ij <  a ij , X ij >  b ij , i = 1,2, • — , n , j = 1,2,. — , m .

Кроме этого, отведенные на мероприятия ресурсы могут быть целыми, если они представляют неделимые объекты (это необязательное условие), и не могут превышать его запаса:

m

^ x j < Z, , i = 1,2, — , n .                                                                         (4)

j = 1

В результате, учитывая целевую функцию (3) и ограничения, получаем многокритериальную (векторную) задачу целочисленного линейного программирования [8] следующего вида:

Fk ( Xy ) = У — Ц- ^ max, k = 1,2, ••■, n ;

j = 1 a y - b y

m

У x y ^ Z i , i = ^1,2, . , n ;

^j =^

‘ xy ^ ay, xU UIJ ,

X y - целое, i = 1,2, .., n , y = 1,2, .., m .

Следует отметить, что оптимизационная задача (5) является векторной [7], то есть она требует оптимизации распределения ресурсов по каждому из объектов или строительных мероприятий. С точки зрения организации вычислительных процедур по модели (5), векторная оптимизация достаточно трудоемкая, так как требует проведения вычислений по каждому ресурсу отдельно. Для решения этой проблемы имеется возможность перейти к однокритериальной задаче оптимизации, учитывая то, что задача по каждому ресурсу линейная.

При построении однокритериальной задачи линейного программирования лучше всего использовать метод обобщенной целевой функции [11, 12], когда критерии оптимизации (3) суммируются, формируя общую целевую функцию. Математическая модель задачи целочисленного линейного программирования, которая будет использовать обобщенную целевую функцию, оптимизирующую все ресурсы по единому критерию, будет иметь вид:

nm max;

F ( X y ) = УУ yt i = 1 y = 1 a iy    b iy

-

У x y ^ Z i , i = ^1,2, . , n ;

^y =^

‘ xy ^ ay, x - > b xiy - i^y ,

X y - целое, i = 1, 2,.., n , y = 1, 2,.., m .

Если запас ресурса превышает необходимое количество, то остаток ресурса переводится в резерв. Количество резерва ri можно определить по формуле ri =^Lxy -Zi, 1 = 1,2,.,m.

y '= 1

Решать оптимизационную задачу (6) можно аналитически при небольшом количестве ресурсов и мероприятий (объектов), однако намного эффективней при этом использовать вычислительную технику [13, 14]. Для численного решения задачи был разработан вычислительный лист на базе MS Excel, который позволял автоматизировать вычисления по оптимальному распределению ресурсов на строительные мероприятия.

Методика организации вычислительных процедур

Приведем методику проведения вычислительных процедур в среде MS Excel на следующем примере. Данная методика может быть использована для автоматизации расчетов для любого количества мероприятий или объектов и произвольного числа ресурсов.

Имеем 8 маскировочных мероприятий по проведению строительных работ, в ходе которых требуется распределение 7 видов ресурсов. Данные по мероприятиям и ресурсам приведены в табл. 1.

Таблица 1

Table 1

Вводим исходные данные в расчетный лист MS Excel, как показано на рис. 1.

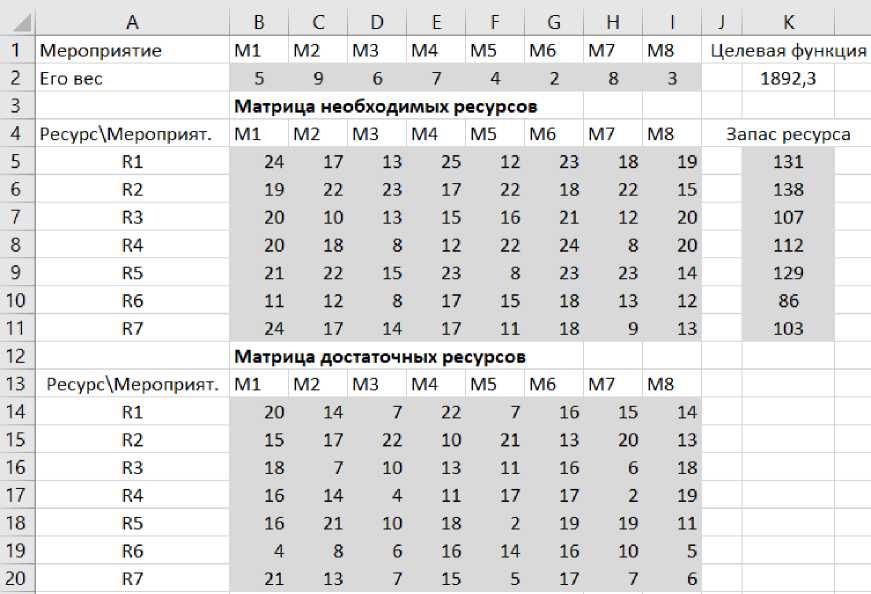
Рис. 1. Исходные данные для автоматизированного распределения ресурсов

Fig. 1. Initial data for automated resource allocation

Исходные данные для примера апробации модели

Input data for the model validation example

Мероприятие	М 1	М 2	М 3	М 4	М 5	М 6	М 7	М 8	Запас ресурса
Вес W i	5	9	6	7	4	2	8	3
Необходимые ресурсы
R 1	24	17	13	25	12	23	18	19	154
R 2	19	22	23	17	22	18	22	15	138
R 3	20	10	13	15	16	21	12	20	107
R 4	20	18	8	12	22	24	8	20	112
R 5	21	22	15	23	8	23	23	14	150
R 6	11	12	8	17	15	18	13	12	86
R 7	24	17	14	17	11	18	9	13	103
Достаточные ресурсы
R 1	20	14	7	22	7	16	15	14
R 2	15	17	22	10	21	13	20	13
R 3	18	7	10	13	11	16	6	18
R 4	16	14	4	11	17	17	2	19
R 5	16	21	10	18	2	19	19	11
R 6	4	8	6	16	14	16	10	5
R 7	21	13	7	15	5	17	7	6

Для решения задачи линейного программирования (6) выделяем под переменные диапазон ячеек В23-I29 и вводим в них произвольные числа, можно их оставить пустыми. Остальные ячейки оформляем в соответствии с рис. 2, расчетные функции в MS Excel приводим в соответствии с табл. 2. Там же приведены параметры надстройки «Поиск решений» (Solver), которая непосредственно выполняет решение оптимизационной задачи.

Таблица 2

Table 2

Расчетные формулы для решения задачи (6) в MS Excel

Calculation formulas for solving problem (6) in MS Excel

Лист MS Excel
Ячейка	Формула	Диапазон автозаполнения
K2	=СУММ(B32:I38)	–
K23	=СУММ(B23:I23)	K23-K29
B32	=B$2*B23/(B5-B14)	В32-I38
К32	=K5-K23	К32-К38
Параметры надстройки «Поиск решений»
Поле		Значение
Ячейка целевой функции		$K$2
Направление оптимизации		Максимум
Изменяемые переменные		$B$23:$I$29
Ограничения		$B$23:$I$29 <= $B$5:$I$11
Ограничения		$В$23:$1$29 >= $В$14:$1$20
Ограничения		$К$23:$К$29 <= $К$5:$К$11
Ограничения		$B$23:$I$29 = целое

В результате исполнения надстройки «Поиск решений» получены результаты, которые приведены на рис. 2.

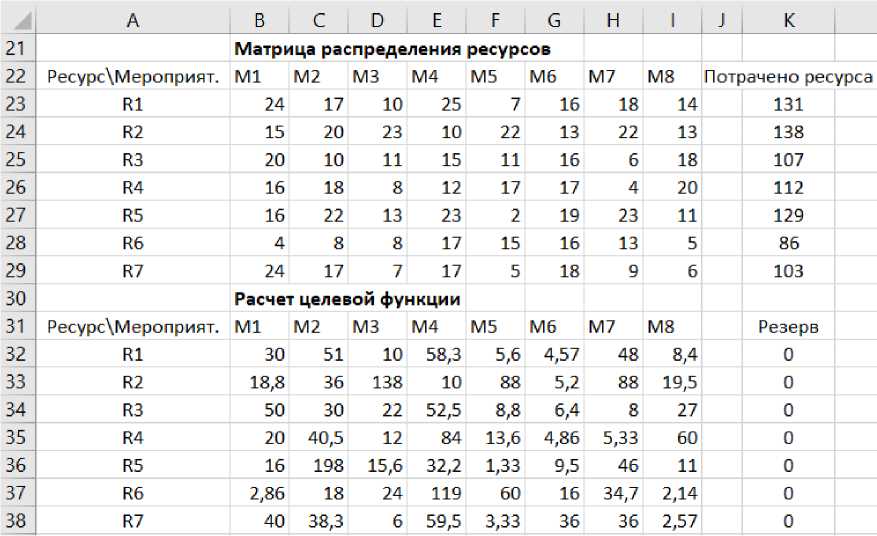
Рис. 2. Результаты распределения ресурсов между мероприятиями Fig. 2. Results of the distribution of resources between activities

Результаты оптимального распределения ресурсов по строительным мероприятиям или объектам приведены на рис. 2 в ячейках В23-I29. Приведенное решение оптимально.

Для проверки адекватности модели распределения ресурсов были проведены вычислительные эксперименты, которые заключались в генерации различных условий для распределения ресурсов на строительные мероприятия или объекты, а затем решалась задача (6) с использованием вычислительной техники. Эксперименты показали высокую устойчивость решения к внешним условиям, отсутствие ограничений на исходные данные и однозначность получаемого результата. Это может служить основанием того, что разработанная модель пригодна для практического использования в планировании и управлении строительными проектами.

Оценка эффективности модели

Предложенная модель распределения ресурсов позволяет определить эффективность применения модели распределения ресурсов на строительные мероприятия или объекты. В качестве критерия эффективности рационально взять целевую функцию вида (2), которая и служит основой оптимизации (6). Тогда показателем эффективности KE как функции от распределения ресурса х ij будет выступать следующий критерий [15]:

nm

KE ( X j ) = ZZ i = 1 j = 1

W j ⁽ a ij - x ij )

.

a ij - b ij

Обозначим через x^c ij , i = 1, 2, …, n ; j = 1, 2, …, m – обыкновенное распределения ресурса без решения оптимизационной задачи (6), а x^* ij , i = 1, 2, …, n ; j = 1, 2, …, m – оптимальное распределение ресурсов, полученное из решения (6).

Поясним смысл распределения xcij. Это распределение ресурса между мероприятиями предполагается получить лицом, принимающим решение по планированию и управлению строительными проектами, на основании интуиции и опыта. Обычно это распределение находится между необходимым и достаточным ресурсом и подбирается так, чтобы выполнялись требования ограниченности ресурса (4). Считая, что это распределение равномерное, для моделирования распределения xcij можно использовать формулу x% = aj +Y(bij -aj), i = 1,2,^,n, j = 1,2,^,m, (8)

где у - некоторый параметр, который подбирается максимально большим с условием выполнения ограничения (4).

На основании этого с учетом (7) эффективность E применения модели распределения ресурсов при проведении маскировочных мероприятий будет равна

E =

KE ( x^c _/;) - KE ( x * ) ---L_3 j Z i_3 L0 . 100 %

KE ( x^c ij )

nm        ^c nm       ^*

^ ^ W j ^{( a}j  ^x j ) - ^^ W j ^{( a}j ^x j )

i = 1 j = 1 ^aij - ^bij        i = 1 j = 1 ^aij - ^bij

nm zz i = 1 j = 1

W j ( a j - x cj ) ^aij ^{- b}-j

• 100%.

Для обоснования эффективности были проведены вычислительные эксперименты, суть которых заключалась в следующем.

Случайно генерировались необходимые и достаточные ресурсы для каждого мероприятия или объекта, а также запасы ресурсов. При этом количество видов ресурса и число мероприятий также было различным.

Затем для каждого эксперимента по формуле (8) генерировалось обыкновенное распределение ресурсов x^c ij и на основании решения оптимизационной задачи (6) вычислялось оптимальное распределение x^* ij . Далее вычислялась эффективность для каждого эксперимента по формуле (9). Вычисления были реализованы в среде MS Excel с использованием надстройки «Поиск решений».

Например, для данных, изображенных на рис. 2, обыкновенное распределение ресурсов x^c ij приведено в табл. 3.

Таблица 3

Обыкновенное распределение ресурсов для данных из рис. 2

Table 3

Ordinary resource allocation for the data from Fig. 2

Ресурсы	Мероп				риятия
	М 1	М 2	М 3	М 4	М 5	М 6	М 7	М 8
R 1	24	17	13	25	12	23	18	19
R 2	16	19	22	12	21	15	20	13
R 3	18	7	12	13	13	18	6	20
R 4	18	16	6	11	19	19	4	19
R 5	21	22	15	23	8	23	23	14
R 6	5	8	6	18	16	18	10	5
R 7	23	15	9	16	5	17	9	9

Были проведены более 50 вычислительных экспериментов, которые показали, что средняя эффективность оптимального распределения ресурсов по сравнению с обыкновенной составляет 34,513 % (для примера данных из рис. 2 эффективность составила 36,25 %).

Заключение

В данной работе описана разработанная и основанная на методах векторной оптимизации математическая модель, которая позволит оптимально распределять ограниченные по запасам ресурсы разного вида между строительными объектами или строительными мероприятиями или работами с целью повышения эффективности выполнения строительных проектов.

При этом получены следующие основные результаты:

• –    на математическом языке поставлена, разработана и обоснована математическая модель распределения ограниченных ресурсов между строительными объектами, работами или мероприятиями;

• –    описана методика проведения вычислительных процедур для реализации модели в численном виде в среде MS Excel;

• –    на основе вычислительных экспериментов была оценена эффективность применения модели распределения ресурсов при управлении строительными проектами, которая в среднем составила более 34 %.

Таким образом, предложенная модель распределения ресурсов приводит к значительному увеличению эффективности организации и управления строительными проектами [16] и увеличивает вероятность своевременного их завершения с минимальными затратами.