Математическая модель посевной и посадочной машины

В современных условиях технология посева сельскохозяйственных культур должна отвечать требованиям повышения продуктивности, ресурсо-, энерго-, влаго- и трудосбережения, защиты почв, экологической безопасности.

В реальности производство сельскохозяйственных культур при использовании сложившихся технологий посева и существующей техники в среднем по России, в частности по Забайкалью, урожайность остаются низкой.

Основные направления технологии посева и способы достижения показателей эффективности приведены в таблице 1.

Таблица 1

Направления развития технологии посева сельскохозяйственных культур

Технология посева	Способы достижения показателей эффективности
Высокопродуктивная	Качество семян. Факторы прорастания семян. Оптимальная густота. Вегетационный период. Оптимальные сроки сева. Равномерность площади питания.
Влагосберегающая	Прямой посев. Посев по мульчирующему слою из измельченной соломы. Совмещение операций. Посев под пленку.
Почвозащитная	Посев с минимальной обработкой почвы. Совмещение операций. Разбросной посев широкозахватными разбрасывателями. Уменьшение уплотнения почвы движителями.
Ресурсо- и трудосберегающая	Посев с минимальной обработкой почвы. Разбросной посев. Совмещение операций. Точный высев.
Экологически безопасная	Посев с локальным внесением основной дозы удобрений. Посев под пленку. Рассадный способ.

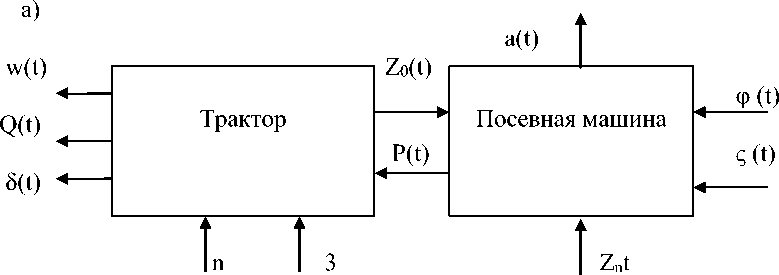
Для посевного агрегата, состоящего из колесного трактора и прицепной сеялки, динамическая модель может быть представлена схемой, изображенной на рисунке 1 а.

На посевной агрегат действуют непрерывно изменяющиеся возмущения, обусловленные многими факторами, главные из которых:

‒ неровность рельефа поверхности поля – Z n (t), воздействующая на посевную машину через опорные колеса и рабочие органы (сошниковые группы) благодаря изменению глубины заделки семян;

‒ физико-механические свойства почвы – ς(t) (механический состав, структура, влажность, твердость, плотность и др.);

‒ воздействие трактора на посевную машину – Z 0 (t), возникающее при его движении по неровностям рельефа поверхности поля.

Под воздействием этих возмущений изменяются выходные показатели, которые определяют эффективность работы посевного агрегата. Основные выходные показатели:

‒ W(t) – производительность агрегата;

‒ Q (t) – расход топлива;

‒ δ (t) – коэффициент буксования трактора;

‒ а (t) – глубина заделки семян;

‒ P (t) – тяговое сопротивление посевной машины.

Если рассматривать отдельно составляющие посевного агрегата (трактор и сеялку), то динамическая модель сеялки может быть представлена по принципу «вход и выход», (рис. 1 б), где для сеялки входными параметрами будут:

‒ Z n (t) – неровность поверхности поля;

‒ ς (t) – неравномерность сопротивления почвы;

• ‒    Z 0 (t) – изменение координаты точки присоединения сеялки с трактором.

Выходными параметрами для сеялки можно считать глубину заделки семян – а (t) и тяговое сопротивление сеялки – P(t). Возмущающие воздействия и выходные переменные являются функциями от времени и между собой слабо коррелированы [4].

Ввиду сложности анализа динамической системы посевной машины с тремя входными и двумя выходными параметрами ограничимся рассмотрением упрощенной динамической модели сеялки (рис. 1 в).

При воздействии силы тяги трактора в процессе работы посевная машина совершает поступательное движение и в то же время под влиянием возмущающих сил совершает сложные колебания. В общем случае математическую модель посевной и посадочной машин можно представить по принципу «вход ‒ выход» в операторной форме: [1]

Y = A( F ) • X,

где Y ‒ вектор выходных параметров [ a (t), P(t), и др.]; X ‒ вектор внешних параметров [Z n (t), ς (t), Z 0 (t)]; А – оператор системы (посевной и посадочной машин), зависящий от внутренних параметров; F ‒ вектор внутренних параметров [f 1 , f 2 …f n ], характеризующий элементы посевной машины (координаты, массу сошниковой группы, опорных колес и механизмов привода и т.п.).

Построение математической модели посевной и посадочной машин заключается в определении вида оператора А=А( F ), определяющего алгоритм преобразования внешних воздействий X [Z n (t), ς (t), Z 0 (t) и др.] в выходные параметры Y [ a (t), P(t) и др.]. Структура оператора зависит от конструктивной схемы машины и от значений внутренних параметров. Поэтому для каждой конструктивной схемы сеялки на этапах разработки и проектирования очень важен вопрос о рациональном выборе внутренних параметров, обеспечивающих необходимое преобразование внешних воздействий и удовлетворяющих агробиологическим, технологическим и энергетическим показателям качества.

На основе агробиологических и технологических показателей повышения продуктивности, с учетом зональных почвенно-климатических особенностей и анализа динамических характеристик сеялок, техническая политика в области технологии посева зерновых должна быть направлена на разработку и внедрение следующих мероприятий:

• ‒    точного посева по глубине заделки семян;

• ‒    посева с локальным внесением основной дозы удобрений в каждый рядок с почвенной прослойкой;

• ‒    прямого посева по фонам измельченной соломы и с минимальной обработкой почвы;

• ‒    бороздового посева для засушливых условий;

• ‒    гнездового посева как средства борьбы с полеганием хлебов;

• ‒    разбросного посева широкозахватными высокопроизводительными агрегатами в зонах достаточного и избыточного увлажнения как средства сокращения сроков сева, уменьшения уплотнения почвы;

• ‒    разбросного посева с локальным внесением основной дозы удобрений и совмещением предпосевной культивации в зонах недостаточного увлажнения, системы загрузочнопосевных комплектов как средства повышения производительности посевных работ;

• ‒    разработкой квадратно-гнездового и пунктирно-гнездового посева, двустрочного посева с преимущественным междурядьем в 70 см для пропашных культур.

  

  Z n (t)         Z n (t)

  
  

  б)

  
  

  f 1       f 2 …   f n

  
  

  Р(t)

  
  

  Посевная машина (сеялка)

  
  

  в)

  
  

  a (t)

  
  
  
  
  

  Z n (t) ς (t)

  Z 0 (t)

  
  
  

  Рис. 1. Динамические модели посевного агрегата (а), посевной машины (б), и упрощенные модели сеялки (в)

  
  

Динамика посевной и посадочной машин по обобщенным координатам φ 0, φ с и α при применении уравнения Лагранжа описывается следующими уравнениями [2, 3]:

• –    в продольно-вертикальной плоскости:

J1 ф. + bp + cp = R0 (t)12 - Ghx + Rc (t)1;(2)

Jpс + b2pc + c2^c = [Fn (t) + Fp (t)]1(3)

• –    в горизонтальной плоскости:

J3(i + b3a + c3a = F(t),(4)

где J 1 – момент инерции сеялки в продольно-вертикальной плоскости относительно точки 0 по координате φ 0 ; b 1 – коэффициент, учитывающий сопротивление изменения положения сеялки по координате φ 0 ; h 1 , l, l 2 – плечи сил R 0 , G, R c относительно точки присоединения с

Вестник ВСГУТУ. № 3 (54). 2015

трактором 0; G – сила тяжести сеялки; R c – результирующая сила, действующая от сошников; R 0 – реакция опорно-приводных колес; с 1 – коэффициент жесткости системы «сеялка ‒ почва»; J 2 – приведенный момент инерции сошника относительно точки О 1 ; с 2 – коэффициент жесткости системы «сошник ‒ почва»; b 2 – коэффициент, учитывающий сопротивление от изменения положения сошника по координате φ с ; F n (t) – возмущающая сила, возникающая при изменении рельефа поверхности поля; F p (t) – возмущающая сила, возникающая при изменении свойств почвы; J 3 – момент инерции сеялки относительно оси прицепа с трактором в горизонтальной плоскости; b 3 – коэффициент, учитывающий сопротивление изменения положения сеялки по координате α в горизонтальной плоскости; с 3 – коэффициент жесткости системы или коэффициент, учитывающий свойства сеялки возвращаться в первоначальное положение по координате α в горизонтальной плоскости.

Подставив в уравнения 2, 3, 4 значения коэффициентов и после некоторого преобразования, получим уравнения в операторной форме, которые в изображениях переменной по Лапласу при нулевых начальных условиях имеют вид [4, 5]:

W ( 5 ) =

k _{0           ;}

T² s ² + t₂s + 1

W_z ( 5 ) =

W p ( 5 ) =

^ z ^{5 2 +} 11k z  .

t 2 s² + t₄5 +1 ’ ^T p ^{5 + 1 ) k} p   .

T²5 ² + T₄5 + 1 ;

W г =

kг

T² 5 ² + T₆5 + 1 ,

где W(s) – передаточная функция сеялки по координате φ 0 ; W z (s) – передаточная функция сошника по координате φ с от действия неровности поверхности поля; W р (s) – передаточная функция сошника по координате φ с от действия неравномерности сопротивления почвы; W г (s) – передаточная функция сеялки в горизонтальной плоскости.

Динамические свойства посевной и посадочной машин в продольно-вертикальной и горизонтальной плоскостях характеризуются передаточными функциями 5, 6, 7, 8, где видно, что сеялка по обобщенным координатам φ 0 , φ с, α совершает колебательное движение. Постоянные времени Т 1 , Т 3 , Т 5 характеризуют инерционные свойства, Т 2 , Т 4 , Т 6 – демпфирующие свойства посевных и посадочных машин.

Увеличением коэффициента демпфирования посевной и посадочной машин возможно уменьшение колебательных свойств сошника.

Выводы

• 1.    Определены уравнения движения посевной и посадочной машин по обобщенным координатам φ 0 , φ с, и α.

• 2.    Полученные передаточные функции характеризуют динамические свойства посевных и посадочных машин.

• 3.    Постоянные времени Т 1 , Т 3 , Т 5 отражают инерционные свойства , а Т 2 , Т 4 , Т 6 – демпфирующие свойства посевных и посадочных машин.