Математическая модель поведения коллектива, учитывающая предыдущие состояния

В работах [2, 3] предложены статистическая и динамическая линейные модели для описания механизмов принятия управленческих решений в коллективе. В этих работах предполагалось, что каждый член коллектива может реагировать лишь на некоторое усредненное «мнение» коллектива по поводу принятия обсуждаемого решения. На практике, как правило, при многоступенчатой процедуре принятия решения на принятие решения индивидуумом влияет как его собственное мнение на предыдущих этапах, так и влияние коллектива. Разумеется, степень влияния коллектива индивидуальна. При этом под влиянием коллектива мы понимаем то обстоятельство, что его мнение может измениться в случае, если ему станет известна точка зрения влиятельной для этого индивида части коллектива (руководителя, коллег-друзей и т.д.).

Эту работу можно рассматривать как продолжение работ [2, 3]

Напомним, принятые в [2, 3] определения и обозначения. Всюду ниже мы говорим о принятии отдельным членом коллектива (индивидуумом) некоторого решения, относящегося к деятельности коллектива. Будем говорить, что индивидуум оказался в состоянии R , если он пришел к выводу о необходимости принятия обсуждаемого решения.

Как и ранее, мы будем предполагать, что.

• 1.    В основе модели лежит гипотеза о том, что в любой момент времени индивидуум, принимая решение о том, чтобы оказаться в состоянии R руководствуется как личным отношением к упомянутому состоянию, так и отношением к этому вопросу окружающих его субъектов (членов коллектива).

• 2.    Будем считать, что отношение к состоянию R каждого индивидуума определяется в фиксированные моменты времени t = 0,1,2,....

• 3.    Будем предполагать, что коллектив состоит из N индивидуумов.

• 4.    Коллектив оказывает влияние на индивидуума с номером j , состоящее в том, что вероятность изменения решения этим под воздействием коллектива ^ нетривиальна, хотя бы для одного j .

Кроме того, будем считать, что

Мы рассматриваем модель с дискретным временем, предполагая, что в отмеченные моменты времени t = 0,1,2,... возможно изменение ситуации по поводу принятия обсуждаемого решения. Указанные моменты могут провоцироваться достаточно стандартными событиями, происходящими в коллективе: общее собрание, изменение качественного состава коллектива, смена руководства,…. Будем считать, что на решение индивида о принятии решения в момент времени t +1 оказывают принятые им решения в моменты времени t и t -1 т влияние коллектива.

Обозначим через р ( t ) вероятность того, что в момент времени t индивидуум с номером j принял решение о том, чтобы оказаться в состоянии R . Будем считать, что начальные вероятности р (0), j = 1,2,..., N известны. Отметим, что эти вероятности могут быть рассчитаны при помощи модели, предложенной в [1].

Сформулированные выше предположения можно формализовать следующим образом:

р ( t + 1) = а р ( t ) + в р ( t - 1) - а , j = 1,2,... N ; t = 0,1,2,...         (1)

где а , ва е [ 0,1 ] . При этом, в соотношениях (1) мы считаем, что P j ( - 1 ) = 0, j = 1,2,..., N .

Мы предполагаем, что на вероятность нахождения в состоянии R в момент времени t +1 оказывают влияние два предыдущих состояния. Основным допущением является при этом гипотеза о том, что влияние на каждого из индивидов равномерно в том смысле, что коэффициенты а,в в модели (1) не зависят от j. При этом, мы вправе считать, что а ? в, т.е., что влияние предыдущего состояния гораздо значительнее, чем прерпредыдущего.

Введем следующие обозначения:

^п ( t ) =

( р 1 ( t П ^р 2 ( t )

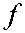
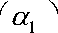
а а

V р ( t L

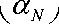
Пользуясь этими обозначениями, запишем систему (1) в векторном виде

П ( t + 1 ) = а П ( t ) + в П ( t - 1 ) - f ,   t = 0,1,2,...

Уравнение (2) исследуем методом производящих функций, полагая

TO

Q(z) = Zп(t)zt, |z| < 1. Умножая (2) на z и суммируя по всем ', получим t=0

jr n ( ' + 1 ) z t = a Z ^ ' ) z + в Тп( t ) z ' - f Z z ' . Отсюда следует, что t = 0                         t = 0                     t = 0                     t = 0

t ^{- 1} Z ^ t + 1 ) z ' ^{+ 1} = a Z ^ t ) z ' + в Z ^ ' - 1 ) z ' ^{- 1} - f Z z ' . Последнее означает, t = 0                              t = 0                        t = 1                              t = 0

что       z ^{- 1} ( Q ( z ) -Q ( 0 ) ) = a Q ( z ) + в ^ ( z ) - ( 1 - z )^{- 1} f .      Но      тогда

(1 - az -в2 )Q( z ) = Q( 0)-z (1 - z)-1 f. Пусть zx, zT - корни многочлена 1 - az - ez2. Ввиду того, что по предположениям a ? в, корни этого многочлена близки к a-1, поэтому можно считать, что zx |> 1, |z2|> 1. Тогда Q( z ) = -р 1 (zxzT ) 1 (1 - zzJ 1) (1 -zz21) (q(0)-z(1 -z)1 f). Поскольку zxzT =- в-, имеем Q( z ) = (1 - zz/) (1 - zz21) (Q(0)- z(1 - z)1 f). Отсюда

TO                 , ОО

Q(z)=Z(zz-1) Z(zz У (Q(0)-z(1-zVf)= k=0

to Г k               A                                             TO      t+1 _  t+1        ..

Z Zz-z-k+j zk(«(0)-z(1 -z)"* f) = Z ,12 zk(n(0)-z(1 -z)"* f) = k=0 < j=0           J                               ’   k=0 z1 z 2 (zx - z 2) V>

TO

=Z k=0

k+1

z1  - z 2

kk z1 z 2 ( z1 - z 2 )

A n ( 0 ) - 2 -- j ^{+ 1} f

V           j = 0        J

TO        k + 1       k + 1

= y            z^k ^ ( 0 )

k z k z k ( z 1 ^- z 2 )    ^{V 7}

-

TO

-z k=0

k + 1       k + 1          to

-z 1__ - z 2___ k^k^S j+ ^{+ 1}

k k(     V Zz f z1 z2 ( z1 - z2 )   j =0

( ^z 1 - z 2 )

TO

z

z ₁

-

z

z k z k n ( ⁰ ) z

-

( ^z 1 - z 2 )

TO

z

z ₁

-

z

z ₂

k z

TO

TO

■k z zj+1 f=z j =0           k =0

k+1      k+1

z1   - z 2      к„ j k k(     VZ z1 z 2 ( z1 - z 2 )

TO

^-4 Z z^ ( ^z 1 ^z 2 ) k = 0 V z 2

zT z k n ( 0 ) ^z

z l    V¹ - k k

^- 7-----7 Z ^z 2 ^z

( ^z 1 ^{- z} 2 ) k = 0

TO

j + 1 z J +

TO              TO

+ 7^2^ Z z - k z k Z z j + 1 f

( ^z 1 ^z 2 ) k = 0         j = 0

Найдем     суммы

TOTO   TOTO

Z z - ^kz^k Z z-f , Z z - z k Z zf .

k = 0         j = 0          k = 0         j = 0

Очевидно,

да             да              да ( s        Л             да

X z - ^kz^k X zf = X X z - j zf = X k = 0         j = 0           s = 0 у j = 0      у          s = 0

1 - z ₂

s - 1

- 1

1 — z₂

z

sf=X s=0

z s ^{+ 1} - 1

^z 2 ^{( z} 2    1 )

zsf

да

=X k=0

k + 1

z ₂

k z 2 ( z 2

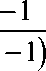
k z^k f .

да             да              да ^k + 1

Аналогичным образом, X z-kzk X zjf = X —r1     zkf. Но тогда k=0        j=0         k=0 z1 ( z1 - 1)

1     да/__\             _ _     да    _k + 1  1             _     да    _k + 1  i

Q ( z ) =

,  ¹  . X z - z ² z ^Q( 0 ) + / z ¹ z x X "T7 Ц z ^k f - / z ² z x X- z ² z ^k f

( z ^{- z} 2 ) ^ ( z 2 ^z 1 J          ( ^z 1 ^{- z} 2 ) ^ ^z 1 ( ^z 1 ^- 1 )      ( ^z 1 ^{- z} 2 ) ^ ^z 2 ( ^z 2 ^- 1 )

Из последнего равенства, пользуясь единственностью разложения в ряд Лорана (см., например, [3]), получаем

t z2       zt - 1

( ^z 1 ^{- z} 2 ) ^z 2 ^{- 1} ( ^z 2 ^- 1 ) j

P j ( t ) ="^-12 P j ( ⁰ ) + тт^ _zt -■- n “ j

^{( z} 1    z 2 / V z 2     ^z 1 У            ^{( z} 1    z 2 ) ^z 1   ^{( z} 1    1 )

j = 1,2,..., N ; t = 0,1,2,... (3)

Формулы (3) позволяют давать некоторые прогнозы на результаты голосования в любой из выделенных моментов времени. Например, математическое ожидание M (t) числа членов коллектива, принявших решение голосовать «за», можно подсчитать следующим образом

N

M (t )=XPj( t )=  — j=1           ( z1 - z -2

z..       z\ - 1 N

^- 7-----7 ^- 1?n X ^a

( ^z 1 ^{- z} 2 ) ^z 2   ( ^z 2 ^- 1 ) j = 1

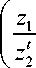
( ^z 1 ^{- z} 2 )

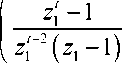
z 2 - ² ( z 2 - 1 ) J

В    частности,

V p (o) + — z ¹-- z ¹—¹—

^j : 1 ^{j ()} ( z 1 - z 2 ) z t ^{- 1} ( z 1 - 1 )

z ₁

( ^z 1 ^{- z} 2 ) v ^z 2

N

- z 2 X P ( 0 ) + ^z 1 У j = 1

N

X a , j = 1

N

Xa j =1

-

t = 1,2,...,

NN

M ( 1 ) =T— Л T¹ -12 X ^Pj ( ⁰ ) + X a - ^{( z} 1    z 2 ) V z 2     ^z 1 у j = 1            j = 1

что

демонстрирует совокупное влияние на матожидание числа проголосовавших «за» после первого этапа. Первое слагаемое полученной формулы описывает

N возможные изменения начального матожидания M (0) = ^Pj (0) за счет j=0

принятых ранее решений каждым из индивидов, второе слагаемое описывает влияние внешних воздействий на каждого из членов коллектива.

Анализ формулы (4) показывает, что при t ^ да

( zx

z 2

( z 1 - z 2 )

t

^ о,

поэтому      для      достаточно      больших      значений

t

х        1           zt - 1

^{M (} t ⁾^(--- '|    —4_Z

⁽ z 1    z 2 ) V z 1    ⁽ z 1    ^X)

z 2 ^- 2 ( z 2 - 1 ) J

N

Z “ j .

j = 1

Это означает, что вопрос о

принятии

решения (M (t)>~^) может быть решен за счет достаточно большого числа этапов и интенсивного суммарного воздействия на коллектив.

N

Z “ j .

= 1