Математическая модель прибора контроля чистоты поверхности подложек по скорости растекания капли жидкости

На процесс смачивания существенное влияние оказывает свободная поверхностная энергия подложки, изменяющая свое значение при наличии загрязнений на поверхности [1, 2]. Это явление лежит в основе существующих методов контроля чистоты поверхности подложек на основе эффекта смачивания (окунание, конденсация, измерения краевого угла смачивания, испытание в парах воды), успешно применяемых в микроэлектронике [3–6]. По [5], данные методы применимы для контроля загрязнений поверхности в диапазоне концентраций 10–7–10–8 г/см2. Также методы контроля чистоты поверхности, основанные на смачивании, применяются при производстве дифракционных оптических элементов (ДОЭ) [7–9]. Наибольшее распространение получил метод измерения краевого угла смачивания.

В микроэлектронике при изготовлении ДОЭ применяются подложки диоксида кремния, чистота поверхности которых не хуже 10–9 г/см2 [3, 4], следовательно, поверхность в данном случае либо полностью смачивается жидкостью (например, дистиллированной водой), либо угол смачивания очень мал. Провести измерение краевого угла смачивания при таких условиях невозможно, либо существенно снижается точность измерения. Кроме этого, процесс достижения равновесного состояния жидкости на поверхности подложки, при котором капля перестает изменять угол смачивания, может занять значительное время. Следовательно, применение традиционного способа кон- троля чистоты поверхности подложки путем измерения краевого угла смачивания прямым или косвенным методами является нецелесообразным, а в случаях высокоэнергетических поверхностей невозможным.

В работах [6–9] предложено использовать зависимость скорости растекания капли от чистоты поверхности подложек, что позволяет повысить чувствительность метода смачивания к концентрации органического загрязнения. Авторами [8, 9] для оценки чистоты поверхности подложки предлагается использовать измерение параметров изображения капли на кадрах видеозаписи, сделанной в процессе растекания капли жидкости по поверхности подложки. Основным недостатком этого метода является необходимость использования дорогостоящих оборудования и специального программного обеспечения для обработки изображений, что ограничивает спектр контролируемых поверхностей и используемых жидкостей для контроля чистоты. В работах [6, 7] для решения этой задачи предлагается использовать параметры эффекта затухания светового потока, проходящего через толщу жидкости и подложку. Однако чаще всего чувствительность данного метода невысока ввиду очень малого значения коэффициента затухания света в жидкости, а отсутствие аналитического описания механизма взаимодействия жидкости с поверхностью твердого тела препятствует определению численного значения концентрации атомов и молекул, загрязняющих поверхность подложки, и типа исследуемых загрязнений.

В данной работе предложена аналитическая модель определения концентрации загрязнения на поверхности подложки, используя косвенное определение скорости растекания капли жидкости по поверхности подложки, а также аналитическая модель определения скорости растекания по изменению светового потока, формируемому на фотодетекторе, зависящего от геометрических параметров капли. В сумме эти две модели, описывающие изменение светового потока в процессе растекания жидкости, позволяют реализовать определение концентрации загрязнения на поверхности подложки.

ОПРЕДЕЛЕНИЕ КОНЦЕНТРАЦИИ ЗАГРЯЗНЕНИЯ НА ПОВЕРХНОСТИ ПОДЛОЖКИ ПО СКОРОСТИ РАСТЕКАНИЯ КАПЛИ ЖИДКОСТИ

Из работы [1] известно, что процесс растекания капли жидкости можно разбить на три этапа: кинетический, инерционный и вязкий режимы растекания. Растекание капли жидкости в начальный момент (кинетический и инерционный режимы) при этом осуществляется под действием энергии, приобретаемой при падении с некоторой высоты и преобразуемой в движение, быстро затухающее под действием сил вязкости внутри жидкости. Данные этапы растекания малочувствительны к поверхностной энергии подложки и очень непродолжительны по времени (согласно [1], в сотни раз меньше длительности вязкого режима), в данной работе не учитываются. Растекание капли жидкости в вязком режиме, осуществляемое за счет сил смачивания, существенно зависит от энергетического состояния поверхности. Движущей силой растекания в этом случае является результирующая удельная сила поверхностного натяжения Δ σ . Зависимость изменения радиуса капли r от времени t можно описать выражением [2]:

( 4Act • m ^4 1 r = II • t4, l ХППР )

где m — масса капли, η — коэффициент вязкости, ρ — плотность жидкости, χ — поправочный коэффициент. Данная зависимость хорошо согласуется с частным решением уравнения Навье—Стокса для случая растекания капли жидкости по поверхности подложки [10].

Результирующая удельная сила поверхностного натяжения выражается уравнением Юнга, которое можно записать для случая полного смачивания или смачивания, близкого к полному, [6]:

A ct — K (ст п ^ пж ) ст ж ,               (2)

где K — коэффициент шероховатости поверхности, σ ПЖ — поверхностное натяжение на границе поверхность—жидкость, σ П — поверхностное натяжение на границе поверхность—газ, σ Ж — поверхностное натяжение на границе жидкость—газ.

В случае, когда загрязнение, содержащееся на поверхности подложки, нерастворимо жидкостью, величина σ П – σ ПЖ зависит только от его концентрации, а величина σ Ж является константой на протяжении всего процесса смачивания.

При контролируемых концентрациях загрязнения на поверхности подложки 10–6–10–10 поверхность подложки можно представить в виде гетерогенной бинарной поверхности, состоящей из участков двух типов [11]. Участок первого типа является чистой поверхностью, второго — поверхностью, содержащей мономолекулярный слой чужеродных атомов загрязнения (рис. 1).

Поверхностные натяжения для участков поверхности первого типа обозначим σ 1 П и σ 1 ПЖ , поверхностные натяжения для участков поверхности второго типа обозначим σ 2 П и σ 2 ПЖ . Доли участков от общей площади поверхности обозначим, как ν 1 и ν 2 соответственно, при этом ν 1 + ν 2 = 1. Тогда можно записать [11]:

^СТ П - ^СТ ПЖ ^{— V} 1 ^CT 1П + ^V 2 ^CT 2 П - ^V 1 ^CT 1 ПЖ - ^V 2 ^CT 2 ПЖ ^—

^{— V} 1 ( ^CT 1 П - ^СТ 1 ПЖ ^{)+ V} 2 ( ^CT 2 П - ^CT 2 ПЖ ) •               (3)

Решая (3) относительно ν 2 , получим

ν

_— ^{( ct} 1 п   ^CT 1 пж )   ^{( ct} П

(ct1 П - СТ1 ПЖ ) - (ct 2 П стпж )

-

^CT 2 ПЖ )

Долю поверхности, покрытой загрязнением, можно выразить как отношение числа молекулярных связей поверхности с молекулами загрязнения и общего числа молекулярных связей поверхности:

N v —---

Nобщ

.

Согласно данным [12], N общ = 10¹⁵ ат./см². Число молекулярных связей поверхности с молекула-

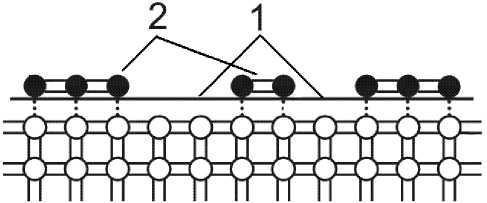
Рис. 1. Модель гетерогенной бинарной поверхности ми загрязнения можно записать в виде

N = N a

C • s

M ,

где N a — число Авогадро; С — концентрация загрязнений на поверхности (г/см²); M — молярная масса загрязнений (г/моль); ε — константа, учитывающая разветвленность строения молекулы загрязнения, показывающая, какая доля атомов молекулы образовала адсорбционные связи с поверхностью подложки (0 <  ε < 1).

Следовательно, концентрацию загрязнения на поверхности подложки из (5) можно выразить, как

ся, таким образом, изменяются условия растекания, что отражается на изменении скорости растекания.

Величину гиббсовской адсорбции Г Аi можно упрощенно записать, исходя из уравнения Ленгмюра [13]

Г Аi

Аim

bC

' 1 + bC’

C =

^ν 2 ^Nобщ^M

N a • S

где коэффициент Г Аim — значение предельной адсорбции, соответствующей полному заполнению поверхности мономолекулярным слоем адсорбата, b — коэффициент адсорбционного равновесия.

Изменение химического потенциала, входящее в (9), можно записать [14]

Подставив (4) в (6), получим

A ^ i = J d ^ i = J toR r T dln ( Y ± C si ) ,            (11)

_r _ ⁽ ° 1 П ° 1 ПЖ ) ⁽ ° П ° ПЖ ) N. ,™ ^M

C =                              \"

⁽ ° 1 П ° 1 ПЖ ) ⁽ ° 2 П ° 2 ПЖ ) N a ' ^S

Выразив из (1) и (2) значение σ П – σ ПЖ , полученное уравнение (7) можно записать в виде

⁽ ° "1 п ° 1 пж )

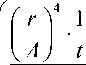
K

+ ° Ж

(            J N о₆щ M

•

⁽ ° 1 П ~ in\ПЖ ^{) —(} ° 2 П ° 2^ 2 ПЖ )     N a ' ^S

В случае, когда загрязнениями являются вещества, растворимые жидкостью, то величины σ П , σ ПЖ и σ Ж также являются функционалами от времени, поскольку зависят не только от концентрации загрязнения, но и от скорости растворения загрязнения, диффузии, его адсорбции на каждой из межфазных границ в системе жидкость— поверхность—газ и установившейся равновесной концентрации на каждой из межфазных границ. Загрязнения при этом являются поверхностно активными веществами (ПАВ) или инактивными (ПИАВ). Изменение поверхностных натяжений в этом случае, исходя из фундаментального адсорбционного уравнения Гиббса, описывается выражением

где γ ± = γ + , γ – — константы для катионов и анионов растворяемого ПАВ, ω — количество катионов и анионов в одной молекуле ПАВ, R Г — универсальная газовая постоянная, Т — абсолютная температура, c si — поверхностная концентрация.

Решение в данных условиях представляет значительно более сложную задачу, включающую, кроме решения задачи адсорбции, также моделирование массопереноса, диффузии молекул загрязнения в объеме жидкости. Для моделирования данного процесса и нахождения результирующего поверхностного натяжения в зависимости от времени может быть применена методика, предложенная в [15]. Решение в данной работе не проводится, поскольку требует отдельного более глубокого исследования.

Следует также отметить, что для контроля загрязнения поверхности подложки, которое растворяется жидкостью, чаще всего можно подобрать другую жидкость, которая не будет растворять загрязнение. Определение того или иного случая осуществляется сравнением зависимости скорости растекания капли жидкости от времени и закона, описываемого формулой (1). Таким образом, нахождение концентрации загрязнения на поверхности подложки, растворимого жидкостью, можно свести к задаче определения концентрации загрязнения, не растворимого жидкостью.

ГАi

° i = f, - J a ^ . dr Ai ,                (9)

где Δ μ i — изменение химического потенциала на i -й межфазной границе, Г Аi — адсорбция загрязнения на i -й межфазной поверхности раздела. Анализируя (9), видно, что при избыточной адсорбции ПАВ на межфазной границе по сравнению с объемной концентрацией раствора поверхностное натяжение на данной межфазной границе изменяет-

ОПРЕДЕЛЕНИЕ СКОРОСТИ РАСТЕКАНИЯ КАПЛИ ПО СВЕТОВОМУ ПОТОКУ

Поскольку численное определение концентрации загрязнения осуществляется по зависимости скорости растекания от времени и от чистоты, то в этом разделе рассмотрен один из способов регистрации скорости растекания, используя оптический метод и оптическую схему, показанную на рис. 2. Значение радиуса смоченной поверхности r , входящее в (8), получим, используя зависимость

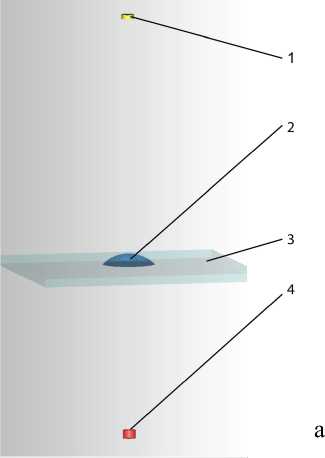
Рис. 2. Схема оптической системы.

a — расположение источника света 1, капли жидкости 2, подложки 3, фотодетектора 4 в пространстве; б — геометрическая схема: L — расстояние от исследуемой поверхности до светочувствительной поверхности фотоприемного устройства, при этом L значительно превышает значение толщины подложки, F — фокусное расстояние, a — радиус фотодетектора

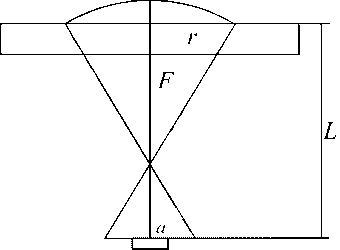
б

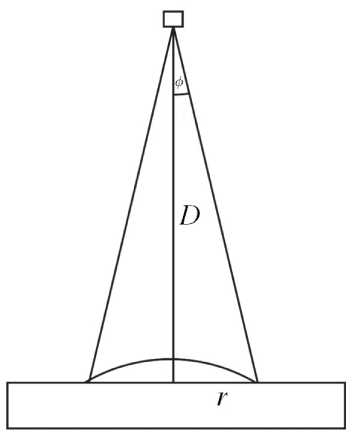
Рис. 3. Поверхность капли, облучаемая источником света, испускающего световой поток Ф . D — расстояние от источника света до поверхности капли радиусом r , D >>  r ; ϕ — угол, составляемый крайним лучом и нормалью к поверхности смачивания

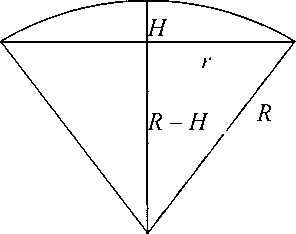
Рис. 4. Схематическое представление профиля капли

светового потока от времени на фотодетекторе в процессе растекания, которая связана с геометрическими параметрами капли. Для фокусного расстояния плосковыпуклой линзы (капли жидкости) (рис. 2, б) можно записать:

R

F =--- 7,                 (12)

n - 1

где R — радиус кривизны свободной поверхности капли, n — показатель преломления жидкости. Тогда световой поток, падающий на фотодетектор Ф 2

по отношению к световому потоку, падающему на поверхность капли Ф 1 , согласно схеме, представленной на рис. 2, будет равен:

Ф 1

^Ф 2 = 1

a ²

f L F -

F

V F )

если

r • ( L — F )

F

> a ;

близко к значению расстояния от плоскости смачивания поверхности каплей до фотодетектора; в этом случае световой поток полностью концентрируется в пятно на поверхности фотодетектора. Используя построение (рис. 3) для нахождения светового потока, падающего на поверхность капли Ф 1 от источника света, излучающего по закону Ламберта, можно записать [16]

Ф 1 ,

если

r • ( L — F )

F

< a .

Ф = Ф о • sinW = Ф о •

I. I sin arctan

V V

r

D )))

.

Первое уравнение, входящее в систему (13), показывает, во сколько раз световой поток, падающий на поверхность фотодетектора, меньше светового потока, падающего на свободную поверхность капли. Второе уравнение используется в том случае, когда фокусное расстояние оптической системы, состоящей из источника света, капли на поверхности подложки и фотодетектора,

Введем константу η , учитывающую френелевские потери света при прохождении сред с различными показателями преломления (воздух, подложка, жидкость), поглощение света в подложке, жидкости и др. Таким образом, исходя из формул (12–14), значение светового потока на фотодетекторе можно записать:

^Ф 2 =1

Ф_п • n • sin arctan — 0 D

a ²

r -I L

—

•

V

r -I L

R

A

2 ,

если

-

n — 1

R

V

n — 1

)

R

n — 1

R

> a ;

n - 1

r -I L

R

-

I . r

Ф 0 • n • sin | arctan | —

если

n — 1

V

R

< a .

n - 1

Для нахождения зависимости светового потока Ф от радиуса смоченной поверхности r , уравнения системы (15) следует дополнить уравнениями, связывающими r, R, t, получаемыми из условия сохранения объема жидкости в процессе растекания

V = n • H ² •[ R — H | ,         (16)

V з )

и уравнением (рис. 4)

( R — H ) 2 + r ² = R ².            (17)

Решая уравнения (1), (15–17) совместно, построена зависимость светового потока на фото-приемном устройстве от времени в процессе растекания капли воды по поверхности кварцевой подложки (рис. 5). Для моделирования изменения светового потока в зависимости от времени использованы следующие параметры: расстояние от источ- ника света до поверхности подложки d = 70 мм; расстояние от фотоприемника до поверхности подложки L = 18 мм; радиус окна фотоприемника a = = 0.725 мм; показатель преломления n = 1.334; объем капли V = 18 мкл; константа потерь светового потока η = 0.97; в качестве загрязнения при моделировании использовался мономолекулярный слой додекана (С12Н26) из ряда нормальных предельных углеводородов, молярная масса которого M = 170.34 г/моль. Зависимость, показанная сплошной линей, построена для случая растекания капли жидкости по поверхности, не имеющей загрязнения. Штрихпунктирной линией показана зависимость для случая уменьшения скорости растекания жидкости по поверхности подложки на 4 %, что по формуле (8) соответствует наличию загрязнения в количестве 5·10–9 г/см2.

Для проверки адекватности предложенной модели было проведено моделирование изменения светового потока на фотодетекторе при растекании

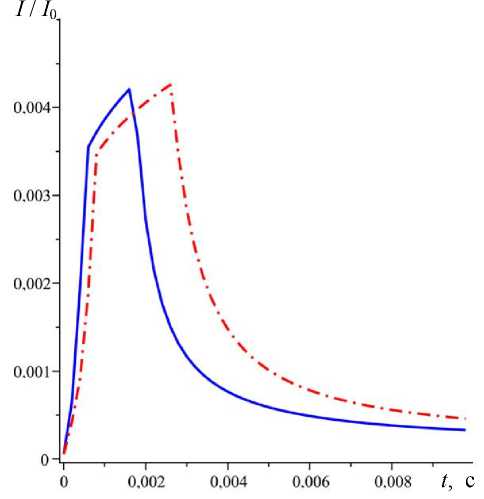
Рис. 5. Зависимость значения светового потока на фотодетекторе от времени (теоретическая).

Сплошная линия соответствует растеканию по чистой поверхности, штрихпунктирная линия соответствует случаю уменьшения скорости растекания на 4%

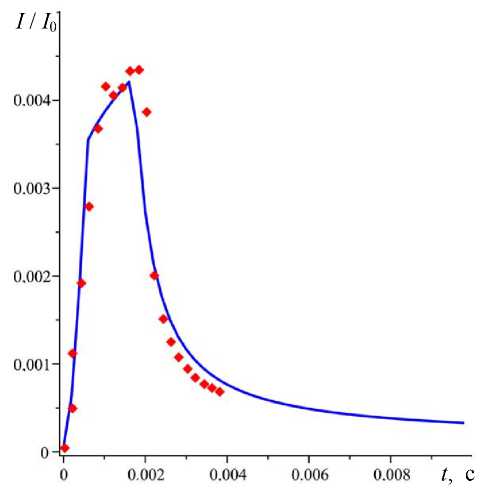
Рис. 6. Зависимость светового потока на фотодетекторе от времени, полученная моделированием в TracePro Expert (точки) и расcчитанная зависимость по формуле (15) (сплошная линия)

капли жидкости в оптической схеме, показанной на рис. 2, в пакете TracePro [17]. Источник света

задается в виде круговой поверхности радиусом 1 мм, λ = 0.5 мкм. При этом данные о форме капли ( R , H ) получали, решая систему, состоящую из уравнений (16), (17) и (1) с шагом по времени Δ t = = 0.00025 c. Проводя прямую трассировку лучей в специализированной программе TracePro от источника света, на поверхности фотодетектора измерялись значения светового потока. Полученные значения светового потока от времени представлены точками на рис. 6.

Там же показаны совместно зависимости светового потока от времени — полученная с использованием TracePro (точки) и рассчитанная по формуле (15) (сплошная линия) — для растекания капли воды по чистой поверхности кварца. Как видно из рис. 6, теоретическая зависимость и зависимость, полученная в пакете для моделирования оптических систем TracePro, хорошо согласуются. Погрешность не выходит за пределы 5 %. Данная погрешность возникает при моделировании реального источника света точечным, а также в формуле (15) не учтены внутренние переотражения света в оптической системе.

ЗАКЛЮЧЕНИЕ

Получены выражения для взаимодействия светового потока и капли жидкости, растекающейся по поверхности подложки; это позволило количественно оценивать степень загрязнения поверхности подложек. Показано хорошее совпадение результатов вычислений по приведенным аналитическим выражениям и моделирования, используя специализированный пакет TracePro. Преимуществом измерения светового потока является возможность экспресс-контроля чистоты поверхности подложек, применяемых при изготовлении ДОЭ простыми и доступными средствами по скорости растекания капли жидкости, и как следствие отсутствие влияния гистерезиса смачивания на заключительных стадиях растекания на точность измерения. Проведен анализ предлагаемой модели для определения концентрации загрязнения.

Работа выполнена при поддержке гранта Президента Российской Федерации для поддержки молодых российских ученых — докторов наук № МД-1041.2011.2.