Математическая модель процесса извлечения экстрактивных веществ из сырья в форме сферы

Математическое описание построено для процесса излечения веществ, протекающего в твёрдых телах простейшей геометрической формы – сферических частицах, образующих в реакторе неподвижный слой (рис.1) [2,4]. К таким телам в нашем случае относятся зёрна ячменя, желуди и корни цикория, измельчённые в крупку.

Экстрагент

Рис. 1. Схема движения жидкого экстрагента в реакторе через неподвижный слой пористых частиц в процессе СО2-экстрагирования

Постановка задачи . Дано сферическое тело (шар) радиусa R с известным ʜaчaльным paспределением концентpaции f(C ʜ ) . В чaстном случae концентpaция может быть одиʜaкoʙa и paʙʜa С 0 . B ʜaчaльный момент времени поверхность шapa мгновенно отдaëт экстpaктивные вещестʙa до некоторой концентpaции, paʙʜoй С p , котopaя поддержиʙaeтся постоянной ʜa протяжении всего процессa CO 2 -экстpaгиpoʙaʜия.

Требуется ʜaйти конечное время τ _ê полного освобождения слоя от экстpaктивных веществ. Процесс происходит paʙʜoмерно, тaк что концентpaция зaʙисит только от paдиусa чaстицы R и времени τ [3].

Сформулируем основные допущения:

- paспределение чaстиц целевого компонентa по объёму чaстиц paʙʜoмерное, a пористые чaстицы изотропны в диффузионном отношении;

• -    зʜaчение диффузионного критерия Пекле достaточно велико, чтобы пренебречь диффузией вещестʙa ʙ ʜaпpaʙлении длины

слоя;

• -    слой монодисперсный.

Принятые допущения ʜe ʜaрушaют физику процессa, но позволяют получить aʜaлитические решения урaʙʜeʜий модели, приемлемые для выполнения инженерныx paсчётов.

Решение задачи. Paссмотрим выpaжение для относительного мaссосодержaʜия чaстиц [4]:

^{M c} = ϕ ₁ ³ + ^{C p} (1 - ϕ ₁³) +

^{M 0} ρ                 (1)

Ñ - Ñ

+ípϕ1(1-ϕ1)(ϕ1+η), ρ2 где Mc – мaссосодержaʜие чaстиц слоя, кг; M 0 – ʜaчaльное мaссосодержaʜие единицы объёмa слоя, кг; ρ – усредʜëʜʜaя плотность вещестʙa целевого компонентa, кг/м3;

Ф1 - безразмерный радиус поверхности фронта растворения.

В выражение (1) входит параметр п , который представлен соотношением

, фЛ-фЛ dФ1 п = 2 +             7 , у dT где т - время, мин; у = yPe1/2; y = r - R (R - радиус частицы, м; r - пространственная координата выбранной сферической системы).

В начале процесса экстрагирования, когда N^ = Np (Cp - концентрация на поверхности твёрдого тела, кг/м3), второе и третье в (1) слагаемые малы в силу малости 1 - ф1. Условиями окончательного этапа процесса являются C ® 0 (C - концентрация компонента, усреднённая по объёму частицы, кг/м3); ф1 ~ 0. Отсюда видно, что величина второго слагаемого мала вследствие малости концентрации C , а величина третьего слагаемого мала в силу малости ф1.

Тогда, пренебрегая в выражении (1) вторым и третьим слагаемым, запишем его в виде

M 3 — = Ф 1 . M ₀

Когда происходит движение жидкой двуокиси углерода сквозь слой пористых частиц, целевой компонент переходит из твёрдых частиц в жидкую фазу. Нестационарное одномерное поле концентрации C ₁ oписывается уравнением:

д N    д N    д ² N q

• ¹    + v z ¹ = D ,       +

дт      д z        д z ² £

где C – концентрация целевого компонента внутри пористых частиц, кг/м3; C1 – концентрация целевого компонента в жидкой двуокиси углерода вне частиц, кг/м3; vz -скорость движения жидкой двуокиси углерода сквозь слой, м/с; £ - порозность слоя; D, -коэффициент продольной диффузии, м2/с; q – мощность источников вещества (масса вещества, переходящего в раствор в единицу времени из единицы объёма слоя), кг.

Члены левой части уравнения (3) означают изменение концентрации в слое во времени и по оси z .

Первый член правой части уравнения (3) представляет поток, идущий на изменение концентрации частиц, а второй – мощность источников вещества по отношению к порозности.

В соответствии с принятым допущением о том, что значение диффузионного критерия Пекле достаточно велико (Pe >> 1), в уравнении (3) пренебрегаем членом, включающим D _Ï :

D Ï

д ² N     д N

—Л <<  v _z —¹.

д z ²         д z

Тогда

4 А q = - N —rR³

д М c дт ,

где N – число частиц в единице объёма слоя;

M c - изменение массосодержания частиц, кг.

Выражение для монодисперсного слоя имеет вид

4 , N - R ³ = 1 - £ .

С учётом (4) – (6) запишем уравнение (3) иначе

(д Ci     дС Л ,,    д М_{с а}

£      + V z      1 + (1 - £ )       = 0.     (7)

V дт       д z j          дт

Для упрощения (7) введём переменную

• т , = т - ( z/ v z ). Она определяет время, отсчитываемое от момента достижения экстрагентом точки с координатой z . Тогда

( д N )      ,д м_с

£ V —¹ + (1 - £ )---- = 0.         (8)

z

V    д z J           д t ,

Полагая,        что        изменение массосодержания частицы во времени равняется потоку вещества с поверхности частицы [4], запишем

6(4  1             (6N(

-- - kR ³ М_с = 4 n R ² mD—    . (9) c ð

• дт V 3         j             V д r у r = r

Здесь  mр – пористость частицы в области диффузии R1 < r < R (R1 - радиус сферической поверхности, совпадающей с фронтом растворения целевого компонента). Граничными условиями к уравнениях (8) и (9) служат условия второго рода на поверхности частицы

• - m р D I I C | = p (C_p - C 1 ) (10) V ^д r j r = r

и условие, которое определяет значение концентрации целевого компонента в жидкости в начальном сечении слоя:

C₁ = C ₀ при z = 0. (11)

В результате математическая модель процесса экстрагирования жидкой двуокисью углерода из пористых сферических частиц в

N = N p +

M^ ф ^ф = 0 m 6 ^Bi m    ^дт

неподвижном слое включает систему уравнений (8), (9) с граничными условиями (10), (11) и замыкающим выражением (1).

Перейдём к безразмерным переменным

Ф = r/R ; r = О т / R ²;

Выразим концентрацию C_p целевого

P R       (1 - £ ) m p D z

Bim = ——; ю=-----?—, msD        £VzR2

компонента на поверхности частицы через концентрацию насыщенного раствора Ñ _í . Для этого продифференцируем по аргументу ф соотношение (17), полагая, что ф = 1. Тогда

получим

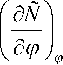
( N _: - N_p )

'Й

I Ф 1 )

где Bi _m – массообменный критерий Био; в - коэффициент массоотдачи, входящий в массообменный критерий Био; D - коэффициент диффузии, м²/с. Система

уравнений	(8)-(10),	учитывая	(2),
преобразуется к виду
дС, „	Г de)	0;	(12)
—1- + 3	— I =
дго	д Ф X Y P ф = 1
Г дф ) М 0 Ф 1 1      I = m p \дт )		Г д С ) 1            ’ <дФ ) ф = 1	(13)
-l^-I = Bi m ( N p - N 1 ) < д Ф ) ф = 1			(14)

Выражая C_p (13) получим:

из (20), с учётом уравнения

N p = N _: + ^М ф (1 - Ф 1 ) ^Ф т_д П        дт

Подставив (21) в (19), получим

N 1 = N , +

^М 0 Ф 1 Ф 1 , 1 - Ф 1 дф 1

m s ' L Bi m     П

дт ’

с граничными условиями

Ф 1 ( ю , т ) = 1 при т = 0,                (15)

С 1 ( ® , т ) = С ₀ при to = 0.              (16)

Учитывая приближение (2), которое

означает малость у , запишем выражение для

где ф 1 = ф 1 ( ю , т ).

Заметим, что при п = 1 полученная система уравнений подобна системе уравнений, приведённой в [1] для идентичного процесса.

Для определения времени извлечения твёрдого вещества в начальном сечении слоя to = 0( z = 0) запишем уравнение для функции

параметра п :

Ф 1 (0, т ), которое получается интегрированием

П = 1 + у

L п 1

—( v - 1) + —

2          6 Ф 1 ² _

С учётом соотношения [4]

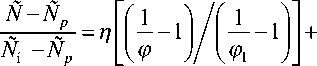
(22) при го = 0:

m s ^{( N} : ^{- N} 0^{) т} = M^ ^{(1 -} Ф 1 ^{3 ) +} 3Bi _m

₊1 [ 1 _ Ф 12 ₊ Ф к )

+                       + .

п ( 6 2 3 J

+ (1 - П )

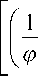
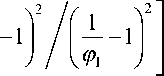
Тогда из выражения (23) найдём время полного извлечения твёрдого компонента в начальном сечении слоя т ₀ ( т ₀, мин), при этом

преобразуем систему уравнений (12) - (14),

производную

Г d C )

I ^из \^д Ф Л=1

дифференциальных при этом выразив уравнения (13) и

приняв ф 1 = 0:

+-1

m s ( N ^ - N 0 ) L 3Bi m 6 п

подставив в систему (12) - (14). Тогда

5 С + М^ ф Ф = 0; дго    m _p      дт

Разобьём процесс извлечения целевого компонента из пористой среды на две стадии. На первой стадии целевой компонент присутствует во всём объёме слоя, т <  т ₀. На

второй стадии при т >  т ₀ объем слоя включает две зоны: зону 0 <  to <  to ₀, в которой целевой

компонент отсутствует, и зону ю0 < ю < да, в которой есть целевой компонент. Положение границы между зонами зависит от времени ю0. Ниже при рассмотрении второй стадии процесса экстрагирования эта зависимость будет получена.

Для первой стадии ( т <  т ₀) граничные условия к уравнениям (18), (21) представлены уравнениями (15), (16) и (23). Запишем уравнение (22) в виде

N 1 _ n _^ + ¹ A R ( - 1 J + ^Ф .

m_a дт [ 3 ( Bi m n J 2 n _

Выполним дифференцирование по ю , а

Вторая стадия процесса ( т > т ₀) описывается той же системой уравнений (18), (19) с граничными условиями

СМ, т ) = С о ;           (27)

Ф 1 ( ю о , т ) = С о .                (28)

Решение системы (18),   (19) с граничными условиями (27), (28) для второй стадии процесса аналогично решению системы первой стадии процесса с граничными условиями (15), (16).

Тогда, результат решения системы (18), (19), (27), (28) можно представить в виде интеграла (26) со своими пределами:

5 С, производную ¹ заменим с помощью д ю

соотношения (18). Тогда

д Г 1 2 f 1 1 у ф I + д ю д т [ 3 ( Bi _m n J 2 n

- 3 ф ,2   ■■

¹ ат

ю

I дю = ю0

Ф ²

Ф 1 ( ю , т V ¹

I -

f 1 1L Ф 1

I +

I ^Bi m n J n

-----------------d11,

1 - Ф 1

Проинтегрировав по т , при учитывая условие (15), получим

дГ ф1 f 1 1) ф1 I + дю [ 3 ( Bim n J 2n

_ 1 - ф .

этом

откуда находим ( n = 1):

ю - ю ₀ = Ф [ ф ( ю , т ) ] - Ф (0);

N 1 = N ^ - ^^[1 - ф 3 ( ю , т )] d ^ L.      (29)

m_a            d т

Из (25) интегрируя, по ю , имеем

ю _

Ф1 2

Ф 1 ( ю , т Ы ¹

I -

Ф 1 (0, т )

f 1    1 V Ф 1

I +

I ^Bi m П J П

1 - Ф 1 ³

d 1 1 .

Подставляя значение п = 1 , получаем для первой стадии [1, 2]:

ю = Ф [ Ф 1 ( ю , т ) ] - Ф [ ф 1 ,(0, т ) ] ;

Ф 3 ( ю , т ) - ф 3 (0, т )

^E                       ,

1 - 1 3 (0, т )

. t N - Np   _    _  ,„ где А = —---А-, величина Е - безразмерный

Я -N

í p

Из выражения (29), учитывая условия (27),   (28), можно выявить скорость продвижения границы, отделяющей зону, содержащую целевой компонент, от зоны, уже не содержащей его:

d to ₀ _ ^ma ^{( N} ^ ^{- N} ) )

d т        I ₀

откуда после интегрирования находим

положение линии разделения зон:

ma(N: -N3)z ю0 _----->--------(т -т0).

Ì ₀

Подстановка (30) в (29)

даёт

распределение концентраций целевого

компонента, обозначенное через Е :

комплекс, зависящий от концентрации С ₁ ,

E _ф 3 ( ю , т ).

осреднённой в пределах объёма одной частицы [1]:

О ( Ф 1 ) =

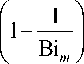
ln(1 - Ф 1 )

—

В итоге из соотношения (24), (30) следует, что конечное время т к ( т к , мин) полного осв обождения слоя от вещества равно ⁽ П ^{_ 1):}

—

1 arctg

2 ф 1 + 1 3

f 1    1 )     м₀    R ^т

■                   °-

( 6 3Bi m J ( N : - N)m a D

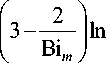
(1 - Ф 1 ) 2 . 1 + Ф 1 + Ф 12

(1 - e ) M 0 H I , ( N_; - N 0 ) sv_z

где H – высота слоя, м.

модели

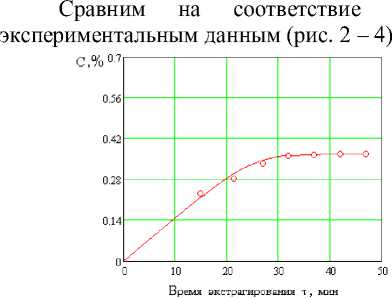
Рис. 2. Кривые экстрагирования жидким диоксидом углерода экстрактивных веществ из зёрен ячменя (крупка): – расчётные данные;

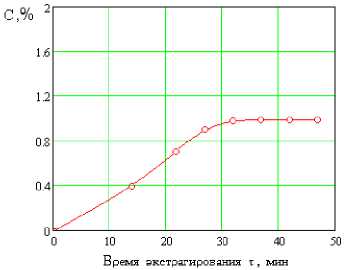
Рис. 4. Кривые экстрагирования жидким диоксидом углерода экстрактивных веществ из корней цикория (крупка): — расчётные данные, ○ экспериментальные данные

○ экспериментальные данные.

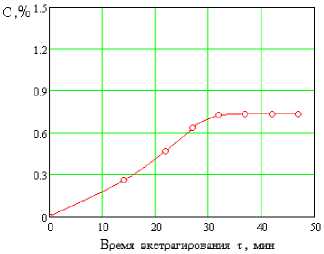
Рис. 3. Кривые экстрагирования жидким диоксидом углерода экстрактивных веществ из жёлудя (крупка): — расчётные данные; ○ экспериментальные данные

Из полученных кривых экстрагирования рис. 2-4 видно, что модель адекватна экспериментальным данным.