Математическая модель процесса потребления вычислительных ресурсов при их неполном освобождении

Бюллетень науки и практики / Bulletin of Science and Practice

УДК 519.248                                        

Современное компьютерное оборудование обладает очень широкими возможностями, изначально оно было разработано для установки только одной операционной системы и для выполнения только одного приложения. Технология виртуализация смогла преодолеть это ограничение и сделала возможным одновременный запуск нескольких операционных систем и выполнение нескольких приложений на одном компьютере при этом такие виртуальные машины оказываются абсолютно изолированными друг от друга и ведут себя, как отдельные физические компьютеры. С помощью технологии виртуализации значительно повышается эффективность имеющегося в распоряжении предприятия оборудования за счет консолидации рабочих нагрузок, что позволяет существенно сократить количество серверного оборудования и снизить эксплуатационные издержки на содержание IT-инфраструктуры предприятия. На сегодняшний день миллионы людей во всем мире используют технологию виртуализации для экономии времени, денежных средств и электроэнергии, достигая при этом более высоких результатов без расширения аппаратных ресурсов [1].

Однако, пользователи виртуальных машин, могут столкнуться с такой проблемой, как утечка вычислительных ресурсов, которая возникает в результате неполного освобождения занятой памяти приложениями. Это приводит к тому, что потребление ресурсов в виртуальной машине неконтролируемо возрастает, в результате может наступить момент, когда новое выделение памяти для исполнения пользовательских запросов становится невозможным.

Поэтому с целью анализа и оптимизации параметров производительности виртуальной машины, актуальным является моделирование процесса изменения объема вычислительных ресурсов при их неполном освобождении при применении технологии виртуализации. Моделированию процесса потребления вычислительных ресурсов, посвящены многочисленные работы отечественных и зарубежных ученых. Значительная часть этих работ отводится применению при моделировании методов теории массового обслуживания [2–5]. Однако модели, разработанные учеными, не исчерпывают все их многообразие, актуальным по-прежнему остается разработка новых моделей, максимально приближенным к реальным процессам.

Математическая модель

В качестве новой математической модели процесса потребления виртуальной машиной вычислительных ресурсов при обработке запросов пользователей с неполным освобождением ресурсов выберем бесконечно линейную систему массового обслуживания M|M|∞ [6–7]. На вход такой системы M|M|∞ поступает простейший поток запросов с интенсивностью λ, время обслуживания запросов пользователей распределено по экспоненциальному закону с интенсивностью µ (Рисунок).

При поступлении заявки (запроса) в систему для выполнения выделяются вычислительные ресурсы, которые в большей степени освобождаются, когда запрос покидает систему. Если в момент поступления запроса недостаточно свободных вычислительных ресурсов виртуальной машины для его обработки, то такой запрос теряется. Будем считать, что потенциальный поток запросов к серверу является бесконечным.

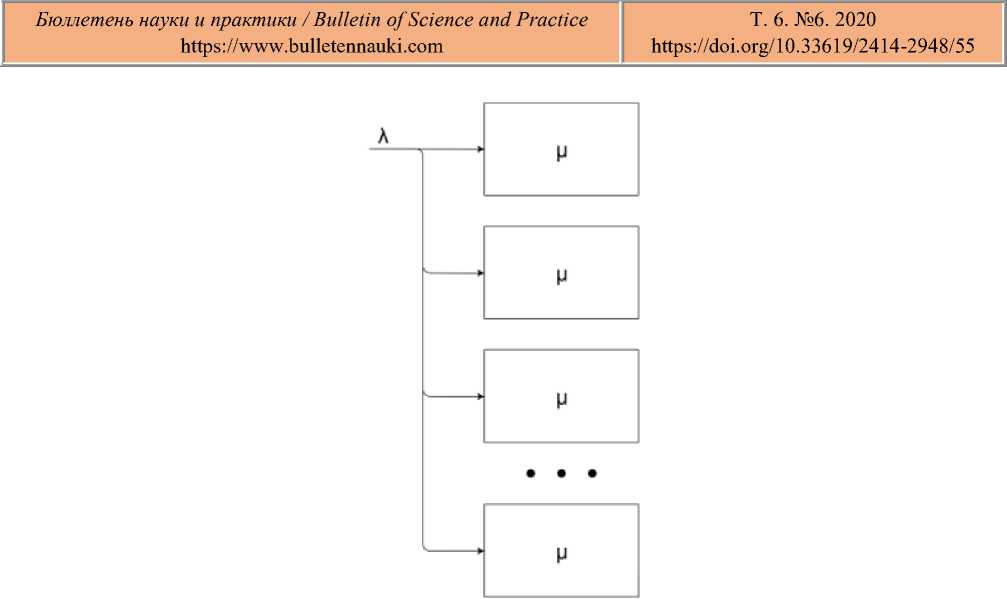
Рисунок. Система массового обслуживания M|M|∞.

Для функционирования данной системы важными являются два случайных процесса: число обсуживаемых запросов k ( t ) в системе и объем свободных вычислительных ресурсов S ( t ). Изменение числа обслуживаемых запросов k ( t ) и объема свободных вычислительных ресурсов S ( t ) происходит в следующих ситуациях:

• 1.    На виртуальную машину поступает новый запрос. Полагая, что поток запросов на машину является простейшим с интенсивностью λ, запишем вероятность того, что за время At на виртуальную машину поступит новый запрос как AAt + о (At) При этом каждый новый запрос связан с захватом некоторого объема ресурсов φ для его обработки. Размер φ является случайной величиной с функцией распределения F^x) и моментам М{^} = а₁ и М{ф²] = ^а2 .

• 2.    В случайный момент времени запрос полностью обрабатывается виртуальной машиной. Будем полагать, что продолжительность обработки запроса является случайной величиной с функцией распределения F(x) = 1 — e^-flt . Каждый запрос обрабатывается и покидает виртуальную машину независимо от продолжительности обслуживания других запросов, с интенсивностью μ. Тогда за время ∆ t запрос покинет виртуальную машину с вероятностью ka At + o(At). При этом каждый обработанный запрос частично освобождает ресурсы некоторого объема η . Размер η является случайной величиной с функцией распределения F|(x) и с моментами М{п} = с₁ и М{ц²} = с₂, причем, учитывая наличие утечки вычислительных ресурсов, всегда с₁< а₁ и с₂< а₂.

Нахождение вероятностных характеристик

В дальнейшем, применяя методы теории массового обслуживания [6–7], а также подход, описанный в [8–9], найдено, что изменение объема свободных вычислительный ресурсов при неполном освобождении ресурсов можно описать выражением: V(t) = у i^(t)       KF)

• -Li=i9 + 1г=1П,

тогда общий объем свободных ресурсов виртуальной машины в момент времени t составит: V(t) = V(0) + V(t), где i(t) — случайный процесс, характеризующей число пришедших запросов за время t, а l(t) — число запросов, завершающих обслуживание в момент времени t.

Тогда средняя величина изменения объема свободных ресурсов за время t составит:

MV(t) = ^ c 1 (1 - e^-^) + Aa 1 t, M V (t) = 7(0) + MV(t)                    ⁽¹⁾

а дисперсия объема свободных ресурсов за время t :

= ~ c₂(1 — e ^- ^) — 2 ^ a 1 c 1 (1 — e "^ ^f) — Xa₂t.

где V (0) — начальный объем свободных вычислительных ресурсов виртуальной машины.

Результатом исследования являются формулы (1) и (2), определяющие вероятностные характеристики величины объема свободных ресурсов виртуальной машины при их неполном освобождении, а именно математическое ожидание и дисперсию.

Заключение

Разработанная математическая модель процесса потребления вычислительных ресурсов и найденные вероятностные характеристики позволяет оценивать и прогнозировать процесс изменения объема свободных ресурсов виртуальной машины во времени и анализировать параметры ее производительности.