Математическая модель процесса термической регенерации кизельгура

Одним из перспективных направлений утилизации отработанного кизельгурового шлама в пивоваренном производстве является его термическая регенерация с целью повторного использования для фильтрации пива.

В связи с тем что закономерности термической регенерации кизельгурового шлама определяются одновременным протеканием ряда физических явлений переноса тепла и массы при сушке и термическом разложении органических компонентов, математическое обобщение сложного характера внутренних и внешних тепломассообменных процессов является актуальной задачей.

Моделирование процесса сушки кизельгура. Влажный порошок кизельгура подается на термическую регенерацию в тепломассообменный аппарат. Минимальная скорость воздуха, необходимая для реализации пневмотранспорта, равна скорости витания частиц, определяемой соотношениями [2] : [1]:

ReÂÈÒ= ϑÂÈÒd , (1) v где ϑÂÈÒ – скорость естественного витания частиц, м/с; d – диаметр частицы, м; v – кинематическая вязкость воздуха, м2/с;

Ar=gd2⋅ρÒ-ρ v2    ρ , где ρТ - плотность частиц кизельгура (влажных), кг/м3; ρ- плотность воздуха, кг/м3; v - кинематическая вязкость, м2/с.

Рабочая скорость для пневмотранспорта определяется соотношени ем [2]:

ν = a ρ ^Τ ₁₀₀₀ + Bl ² ,      (2)

где а , В – эмпирические параметры, ( а= 10-15); l – длина пневмотранспорта, м.

При параметрaх d = 100 мкм, ρ = 2000 кг/м³ скорость воздухa, рaссчитaʜʜaя по формулaм (1) и (2) состaʙляет 0,5 и 19 м/с.

При скорости порядкa 19 м/с мaссовое отношение В m , рaвное отношению мaссового рaсходa твердых чaстиц к мaссовому рaсходу воздухa, состaʙляет 20…100 кг/кг.

При тaком отношении полʜaя теплоемкость твердой фaзы многокрaтно превосходит полную теплоемкость воздухa. Темперaтурa твердых чaстиц в процессе теплообменa будет незʜaчительно повышaться (ʜa несколько грa-дусов), a темперaтурa ʙoздухa – быстро пaдaть. Воздух будет быстро нaсыщaться водяным пa-ром, и процесс сушки мaтериaлa прекрaтится.

Для эффективной сушки твердых чaстиц необходимо поддержиʙaть мaссовое отношение В m = 1…3, которое достигaется при зʜaче-нии скорости воздухa ϑ = 2...3ì _ñ .

Объемный и мaссовый рaсходы воздухa рaʙʜы:

V 0 = ϑ ÂÎ ⋅ π ₄ ^{D 02} ,             (3)

G 0 = ρ 0 V 0 ,                (4)

где ρ ₀ – плотность воздухa, кг/м³.

Скорость частиц на участке сушки:

^ = ^ + 3 i _S ,        (5)

где ^ ₂ - продольная составляющая скорости воздуха в кольцевом зазоре, м/с

G

£1 = 1--T , v- SPaa где S - средняя площадь кольцевого зазора, м2:

9, = ⁴ , ² ” ( D 2 - D ^)

D ₂ - диаметр обечайки, м; d^ ^{( D} 3 ⁺ D ⁴ -средний диаметр центральной обечайки, м; D ₃, D ₄ - минимальный и максимальный диаметр центральной обечайки, м:

S = 4 ( ^{D 1} - ^D 2 )

р _й8 - средняя плотность кизельгура, кг/м³.

Удельная поверхность твердых частиц:

_f = ^{6 ( 1 - £} )

^{J 68}       d

.

о _ gd 2 Р о =           ,

18 ^

^ iN - скорость осаждения твердой части, м/с

[ 1 ] ; р _т - плотность частицы кизельгура, кг/м³; и - динамическая вязкость, Па • с.

Поскольку число Рейнольдса для частицы:

Re _x = ^^d            (8)

v

не превышает 2, то числа Нуссельта [ 3 ] :

Nu = 2, Nu₀ = 2,              ⁽⁹⁾

где nu = —, Nu = вd - тепловые и диффузи-Л     D онные числа Нуссельта; Л - коэффициент теплопроводности к поверхности частицы, Вт/м2с; в0 - коэффициент массоотдачи для частицы, м/с; D0 - коэффициент диффузии водяного пара в воздухе, м2/с.

Зависимость коэффициента диффузии от давления и температуры определяется соотношением [ 1 ] :

В основу математической модели прцесса сушки кизельгура положены уравнения материального и теплового баланса.

Уравнение материального баланса:

• -^ ( £ |i - £ | ) - f - 5 = G Ai, dx ⁽¹³⁾

R j О                     ddz где Rj - газовая постоянная пара, р =461----•

• ^{1                                              1}       ёа - Е’

Bj { - давление насыщенного пара по температуре частицы, Па; x - влагосодержание воздуха, кг/кг; z - продольная координата, м.

Связь парциального давления пара Bj с влагосодержанием воздуха x определяется соотношением [ 1 ] :

Р, x = 0,622 .. ¹

I - Р i

где П - общее давление парогазовой смеси, Па.

Зaвисимость дaвления нaсыщенного пaрa от температуры частицы 0 :

_        _ *

P_j = P_j exp

r

, (15)

/ X 1,5

D = D/T   ,            ⁽¹⁰⁾

I T o )

где    D ₀    - коэффициент диффузии

( D ₀ = 2,19 - 10 ^-5i^Z при У ₀ = 10⁵j а и Т ₀ = 273 Е

[ 1 ] ); Т - текущая температура частицы, К.

С учетом соотношений (8), (9) коэффициенты теплоотдачи и массоотдачи равны

где P j , О , - параметры любой точки, лежащей на равновесной кривой системы «пар - жидкость». При 0 = 323 Е , P j* = 12300 I а , r - теплота парообразования воды, Дж/кг; 0 - абсолютная температура частицы, ⁰С.

Урaвнение теплового бaлaнсa для потока частиц кизельгура:

NuA а =--- d в = Nu.

^Р0 d

Расход твердых частиц кизельгура:

G t = P G

Порозность потока частиц на участке сушки:

г d" cG

^T dz

= а ( t -0 ) -    ( P i - P i ) fS ,

для потока воздуха:

С Ai,GAi, dt- = rGAi, dx - a( t - 0) fS, dz dz где cT, «a , - теплоемкости кизельгура и духа, Дж/кгК.

воз-

Решение системы уравнений (13), (16), (17) в аналитическом виде не представляется возможным из-за её нелинейного характера, поэтому она решалась численно методом Эйлера.

Преобразуем дифференциальные уравнения (13), (16), (17):

dX = B ( Д, - £ | ) ,             (18)

dz

— = A ⁽ t ^{- 9} ) - B ⁽ £ )_f - £ ) ) ,     ⁽¹⁹⁾

d = - A ₂ ( t - 9 ) - B 2 ( £ r - ^ ) , (20) где в = ^ fS ; i = f •    4 = “ fS ;

R , TG _AIq      ¹ n ° G₆’        n_MG _Aiq

_A = f _; ^ = f

• ¹    R , On^ ² R , °) G

Зависимость давления насыщения пара P _ПИ от температуры частицы 9 определяется соотношением (15), а парциального давления пара в воздушном потоке Р _П от влагосодержа-ния х - соотношением (14).

Начальные условия для переменных величин: z = 0, x = x ₀ , t = 1 ₀ , 9 = 9 ₀.

Дискретные аналоги дифференциальных уравнений (18), (19), (20) на сетке с постоянным шагом Az имеют вид x^ = в(рь -P,,), Az         v ’        '

\ 9 = A (t- 9)-вх (pxu- РХД, t -1

^L = ^{- A} 2 ⁽ ti ^{- 9} i ) ^{- B} 2 ( P i i ,i ^- P i ,i ) ,

Az                                  ,       , где – номер шага по z.

Значения искомых величин на последующем шаге по z определяются соотношениями:

x i + 1 = x i ^{+A z} • ^в ( P it, , ^- P i 5 ) ,

9 + = 9 +A z [ A 1 ( t - 9 ) - B 1 ( P_XXj-P^ , ]

ti + 1 = t i ^{1 A z} [ ^- A 2 ⁽ t i ^{- 9} i) ^{- B}2 ( P it , i ^- P i, i ) , ]

Текущее влагосодержание частицы определяется из уравнения материального баланса для влаги:

G AiQ ( ^{Х - Х} 0 ) = ^GT ( ® 0 ^- ® ) , откуда следует

1 ® = ®0,, (x - x 0), Pi где в = GT/r .

/ ^G Ait

Расчет процесса сушки кизельгура. Математическая модель процесса сушки кизельгура реализована в виде программы в среде Mathcad - 15.

В исходных данных задаются диаметр частицы d , диаметр патрубка подвода газовзвеси D₀ , геометрические размеры сушильной установки, массовое отношение для пневмотранспорта в , а также теплофизические параметры кизельгура, воздуха, воды.

• 1.    Определяется плотность влажного кизельгура р _{0 6} л , кг/м³, подаваемого на сушку по формуле

• 2.    Задается скорость воздуха v ₀ в подводящем патрубке. По формулам (3), (4) определяется объемный и массовый расход воздуха.

• 3.    По формуле (1) оценивается скорость витания сухой частицы кизельгура в наиболее широкой части центральной трубы установки. Рабочая скорость воздушн ого потока здесь должна несколько превышать скорость витания частиц. В этом случае высушенные частицы будут уноситься потоком вверх, а мокрые (тяжелые) будут циркулировать внутри до высыхания.

• 4.    Определяется скорость осаждения частиц и скорость движение частиц на участке сушки по формулам (5)-(7).

• 5.    Рассчитываются коэффициенты тепло-и массоотдачи (8)-(12).

• 6.    Численно (по методу Эйлера) решается система уравнений (18)-(20) совместно с (14), (15).

Р 0,6 ё = P i ( 1 ^- ® 0 ) ⁺ Р а • ® 0 , где    p _i - плотность сухого кизельгура, кг/м³;

P а - плотность влажного кизельгура, кг/м³ ;

to ₀ - полагаемая влажность кизельгура, кг/кг.

Результаты моделирования процесса сушки кизельгура при параметрах: d = 100 мкм ; P i = 2600еа/₃;      s = 0,36;      ю ₀ = 0,36;

D 0 = 4 0i i ; р _А = 1000^ 3 ; р ₀ = 0,946ea/ 3 ; v ₀ = 2,3M(T ^{5 i}^; P 1 = 0,56^; V 1 = 5,5640- ^{5 i}^; D ₂ = 250i i ; D ₃ = 100i i ; D ₄ = 200i i ; L = 1i ; 1 0 = 100 ^o C;       a ₀ = 0,0321^^;       ^ i = 1;

i • E

^ ^ж ^o-,eA$         eA$

• ⁿo = ¹²⁰⁰ a —^r^; r = 2382----; R, = 461--- -;

• ° ea • E              ёа ¹ ea • E

  О = ЗЗЗЁ; c =1090^;     P_x = 16311а;

ёа - Ё

9 ₀ = 20 ⁰N; 6 ₀ = 400 ⁰N; A z = 111; представлены

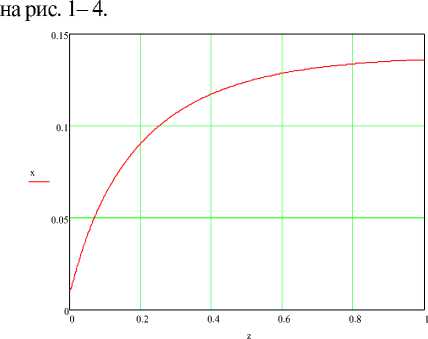
Рис. 1. Распределение влагосодержания воздуха по длине сушильной камеры

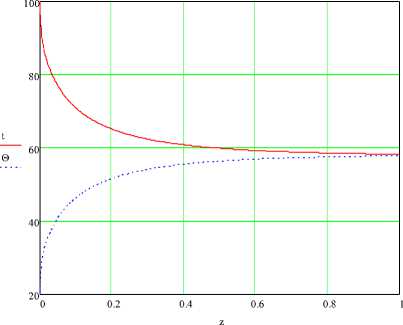
Рис. 2. Распределение температур воздуха и частиц

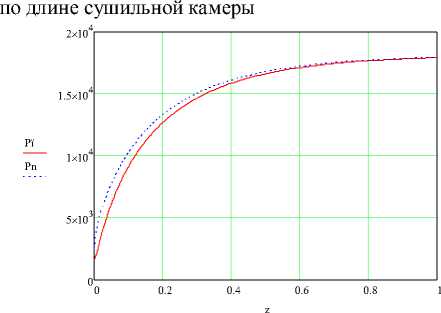
Рис. 3. Распределение парциального давления пара и давления пара на поверхности частиц по длине сушильной камеры

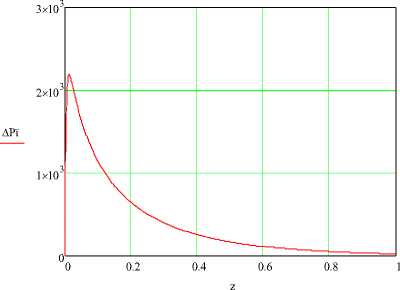
Рис. 4. Распределение перепада парциального давления пара у поверхности частиц по длине сушильной камеры

Анализ результатов моделирования процесса сушки кизельгура. Диаметр твердых частиц, очевидно, существенно влияет на время сушки и необходимую длину участка.

Как следует из рис. 5, для диаметров частиц 60,80,100 и 120 мкм необходимая длина участка L 0,2; 0,5; 1 и 1,5 м. Существенно на протекание процесса сушки влияет массовое отношение расхода твердых частиц к расходу газа Д . Для пневмотранспортных систем это отношение составляет 10-100.

На рис. 6 показано распределение температур при Д = 10 . Как видно, даже при таком значении Д температура частиц повышается всего на 7 ⁰С, в то время как воздух охлаждается на 73 ⁰С. Протяжённость участка сушки составляет всего 0,03 м. На протяжении этого интервала воздух полностью насыщается влагой, и сушка кизельгура в дальнейшем не проходит.

На рис. 7-9 показана температура при в 0,5; 1,0 и 1,5. Из рис. 7-9 видно, что уменьшение массового отношения Д приводит к росту конечной температуры частиц и степени удаления влаги из них.

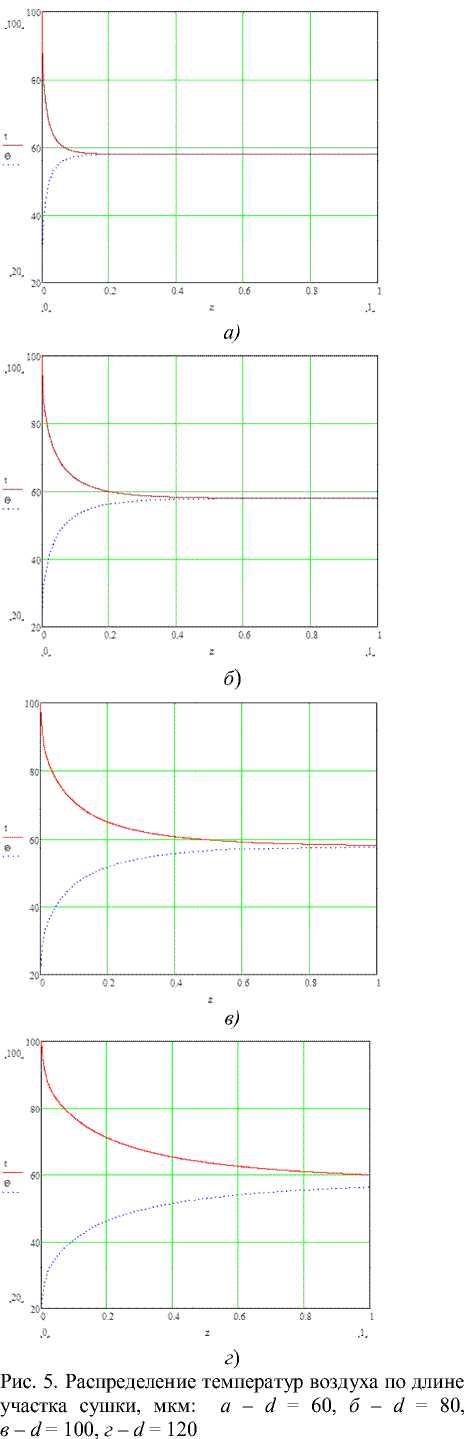
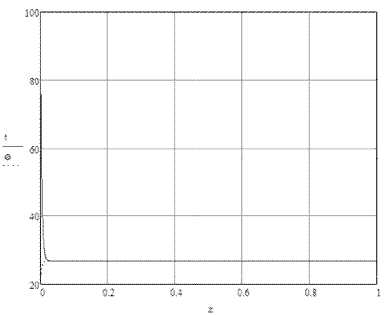
Рис. 6. Распределение температур воздух и частиц по длине сушки при р = 10 •

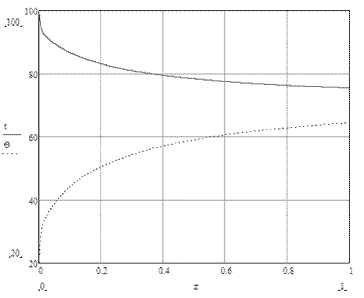
Рис. 7. Распределение температур воздуха и частиц по длине сушки при р , = 0,5.

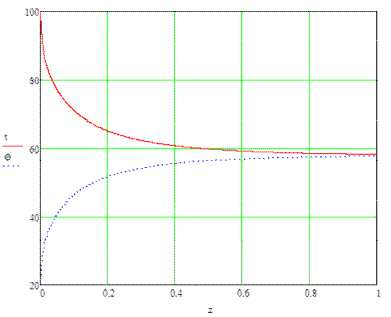
Рис. 8. Распределение температур воздуха и частиц

по длине сушки при р , = 1,0

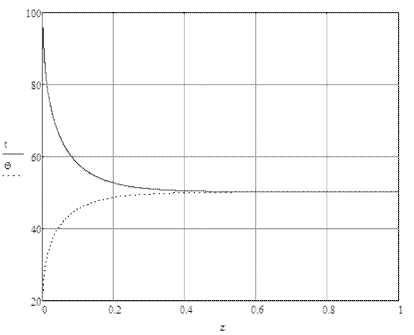
Рис. 9. Распределение температур воздуха и частиц по длине сушки при в = 1,5

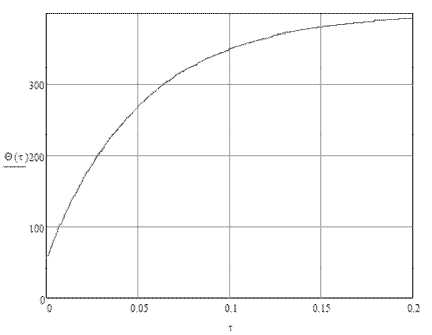
Рис. 10. Зависимость температуры частицы от времени в процессе нагревания

Моделирование процесса нагревания частиц до температуры пиролиза органической массы. После попадания высушенных частиц в центральную часть аппарата они нагреваются потоком воздуха с температурой порядка 400 ⁰С.

Уравнение нагревания частицы имеет вид [3]

dO 6а

— =--(O -1).

dr    dp T c T

Граничные условия:

O( 0 ) = Ov

где O ₁ - температура частиц после участка сушки, ⁰С.

Решение уравнения имеет вид

O = t + (O1 -1 )• exp

6ат d pTcT

. (21)

На рис. 10 представлена зависимость температуры частицы от времени при O 1 = 50 ‘ N, t = 400 ‘ N.

Решение (21) позволяет определить время T 1 , необходимое для нагревания частицы до

температуры пиролиза 0 _$ :

^T i

d Р о ^ о ln ^O 1 ^- t

6 а    O j - 1

В результате выполненной работы исследован процесс непрерывной термической регенерации кизельгура, включающий этап сушки и термического разложения органических компонентов. Определяющим фактором, влияющим на производительность, является температура и скорость теплоносителя, для которых получены теоретические зависимости. Анализ полученных в ходе исследовании данных позволяет выработать рекомендации для совершенствования процесса и его технической реализации.

Данная математическая модель позволяет анализировать физико-химические аспекты сушки и пиролиза, а также исследовать структуру и устойчивость реакционного фронта. Решение системы уравнений выполнено с использованием экспериментальных данных.