Математическая модель процесса ультрафильтрационного концентрирования вторичного молочного сырья в трубчатом мембранных аппаратах с фильтрующими элементами типа БТУ 05/2

This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International License

Родионов Д.А. и др. Вестник ВГУИТ, 2021, Т. 83, №. 1, С. 36-43 Введение

Рассматривается задача оптимального планирования проекта. Для управления техническими системами и технологическими процессами применяются методы математического моделирования и оптимизации технологических процессов производства. При построении системы автоматического управления мембранным процессом рекомендуется использовать усовершенствованную математическую модель, позволяющую прогнозировать параметры мембранного разделения.

В работе [1] авторы описывают процесс ультрафильтрации молочной сыворотки для выделения белков с раздельным отводом части потока концентрата и математические модели этого процесса. Приведена формула расчета коэффициента обогащения концентрата. Построена математическая модель процесса уменьшения производительности мембраны из-за блокирования пор сгустками геля.

Авторами [2], на основе балансных соотношений разработана эмпирическая модель процесса ультрафильтрационного концентрирования и деминерализации подсырной сыворотки с учетом величины осмотического давления вторичного раствора молочной сыворотки, позволяющая рассчитывать значения концентрации и объемы пермеата и ретентата в промежуточных камерах и на выходе из плоскокамерного ультрафильтрационного аппарата.

Для описания процесса ультрафильтрации с учетом гелеобразования в условиях периодической очистки мембраны авторы [3] Строили математическую модель следующим образом: 1) толщина образующегося слоя геля δ считается постоянной вдоль мембраны и меняется только с течением времени; 2) свойства геля считаются постоянными; 3) количество пор мембраны, засоряемых за время dt, пропорционально плотности потока; 4) Механическая очистка поверхности мембраны приводит как к частичному удалению слоя геля, так и к частичной очистке пор мембраны; 5) время, затрачиваемое на очистку поверхности мембраны, не учитывается; считается, что изменение характеристик процесса, связанное с очисткой, происходит скачкообразно.

Авторами [4] разработана математическая модель процесса электрогиперфильтрационного разделения промышленных растворов, позволяющая рассчитывать объемные расходы ретентата, а следовательно, и пермеата, по камерам и текущий объем раствора в промежуточной емкости.

В своей работе [5] авторами представлена математическая модель массопереноса многокомпонентных растворов в баромембранных аппаратах рулонного типа. Результатом полученной математической модели является распределение полей концентраций веществ в межмембранном канале.

При моделировании процесса мембранного концентрирования белков молочного сырья авторы [6] Пришли к следующим выводам увеличение концентрации раствора до наибольшего значения состоит в увеличении скорости отвода растворителя, что можно гарантировать только при стабильно высокой селективности мембраны. На практике выполнения этого условия добиться достаточно тяжело, что объясняется наличием концентрационной поляризации, которая начинает проявлять свое негативное влияние достаточно быстро при концентрировании растворов высокомолекулярных соединений. Таким образом, значения параметров β1, β2 зависят от вида и конструктивных особенностей оборудования, а также селективности мембраны в нем.

Авторы в работе [7] предложили математическую модель плоского обратноосмотического канала с двумя полупроницаемыми стенками. В своей работе решают взаимосвязанные системы уравнений, включающая уравнения гидродинамики и конвективной диффузии с соответствующими граничными условиями. Получили распределение скоростей и концентраций растворенного вещества по длине и высоте межмембранного канала. Показали возрастание концентрации в примембранной области по длине межмембранного канала. Авторами проведена проверка адекватности математической модели.

Для прогнозирования процессов разделения эмульсий, выбора оптимальных условий проведения этих процессов необходимы соответствующие математические описания. В связи с этими авторами [8] разработана комбинированная краевая задача для непрерывного процесса конвективной диффузии в пространстве между непроницаемой стенкой и мембраной и молекулярной диффузии в мембране в виде аналитического решения соответствующей системы дифференциальных уравнений нестационарной диффузии для переноса вещества в движущейся жидкости и в мембране, обеспечивающей из-за своих свойств селективной проницаемости разделение веществ.

В работе [9] авторами Получены зависимости для описания работы мембранного модуля. С использованием полученных зависимостей про – ведено сравнение противоточной и прямоточной схем контактирования. При достаточно длинных мембранах различие между схемами контактирования незначительно.

Авторами [10] представлена математическая модель, учитывающая эффекты температурной и концентрационной поляризаций, депрессию пара над раствором. Для пленочных мембран МФФК2, МФФК3, МФФК4 экспериментально определен и проанализирован коэффициент паропроводности. Получены уравнения для расчета температур горячей и холодной поверхностей мембраны, необходимые для определения эффекта температурной поляризации. Предложено модифицированное уравнение паропроводности, с выделением эффекта депрессии пара над раствором и концентрационной поляризации. Для мембранной дистилляции морской воды экспериментально определен и проанализирован параметр, отражающий данный эффект. Разработана методика инженерного расчета мембранно-дистилляционного аппарата.

Автором в работе [11] предлагается модель для расчета концентраций кубовых красителей в разделяемой сточной воде в зависимости от увеличения сопротивления и слоя геля. Результаты экспериментальных данных и расчетных значений имеют отклонение в пределах 2,7–3,1 %.

В работе [12] Предложена новая модель процесса мембранного концентрирования, дополненная не учтенными ранее входными воздействиями, возмущающими воздействиями, выходными параметрами и обратной связью. Это позволяет оперативно вносить необходимые изменения в значения возмущающих воздействий в результате несоответствия полученных значений выходных параметров диапазонам допустимых значений параметров, либо приближения к границам этих диапазонов. Проведен анализ дальнейших перспектив развития математического моделирования мембранных процессов с использованием элементов теории автоматического управления.

Авторами [13] предложена методика моделирования процессов мембранного концентрирования жидких пищевых сред на основе передаточных функций. Проведена структурная и параметрическая идентификация модели процесса концентрирования в мембранном аппарате с отводом примембранного пограничного слоя. Экспериментально подтверждена адекватность модели.

В работе [14] предложена математическая модель процесса мембранного концентрирования молочных сред в ультрафильтрационном аппарате с отводом поляризационного слоя, разработанная на основе методов информационного моделирования и методики, включающей: анализ процесса как объекта моделирования и выявление основных входных и выходных параметров объекта, выбор вида входных воздействий, структурную идентификацию объекта моделирования, выбор критерия близости (функции невязки), определение значений параметров модели (параметрическую идентификацию), проверку адекватности и непротиворечивости модели. Описаны устройство и принцип работы ультрафильтрационного аппарата с отводом поляризационного слоя. Математическая модель процесса мембранного концентрирования реализована программными средствами. Приведены результаты оценки адекватности и непротиворечивости модели экспериментальным данным, на основе которых сделаны выводы о точности математической модели.

Математическое описание мембранных процессов разделения, рассмотренных в работах [1–20], не полностью учитывает кинетику мембранного процесса, включающую диффузионные, осмотические и гидродинамические процессы. Поэтому целью данной работы является, разработать математическую модель, основанную на решении уравнений конвективной диффузии, на основе уравнения Навье-Стокса и уравнения неразрывности потока. Проверить адекватность разработанной математической модели путем сравнения расчетных и экспериментальных данных по кинетическим зависимостям.

Результаты и обсуждение

Математическая запись задачи:

д U д V ~

—+— = о ;

д x    д у

д U	d U	д U	1 д P	Г д 2 u	д 2 U
--+ U-- дт     d x		+ V --=---+ v д у    p д x		+ ч д x   д у
д V	д V	д V	1 д P	г д2v	д 2 V I
— + U —		+ V— = -	+ v	—+
дт	д x	д у	P д У	ч д x 2	д У 2 J

; (2)

; (3)

и d C + V « = D   .

д x     д у     д у

Начальные условия:

С ( 0, y ) = С исх .

Граничные условия для уравнений гидродинамики:

U(x,+R) = 0; U(x, – R) = 0.

Граничные условия с учетом модифицированного выражения для уравнения конвективной диффузии, скорость фильтрации:

k. • e

1           I                       k_

1 +-- 1  1 - exp J --— - k,

( k 1 • E )           ( ^D g •

x

.     .     .     .       д c (x, r )

x C ( x , R ) • V ( x , R ) = D—|---

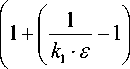
1 - exp J

k^- - k

Dg •     3

,      \          \     d C ( x , - R )

x C ( x , - R ) • V ( x , - R ) = D---

X

. (8)

Рассмотрим решения уравнений гидродинамики:

д и д т	+ и 9и д x	д и    1 д Р + V = S y     p д x	+ v	д 2 и + д 2 и ) ; (9) у д x2   S y )
д V дт	SV + и— д x	д V    1 д Р + V— =--- S y    p S y	+ v	" S2 V   s 2 v у —т + —т ;(10) чд x 2    d y 2 )
		д и  д V 1 д x   д y	= 0	.                (11)

Так как мы рассматриваем стационарный процесс, то можно записать d U  d V A

--+ — = 0 . дт   дт

Тогда система уравнений примет вид:

и + v ^d-U =

—

d x

S y

1 d P

p d x

и V + v S v =

—

d x

S y

( а² и  д² и

+ v „ ₇ + „ ₇ , д x    d y²

1 д P --+ v

P ^S y

д 2 V  d ² V У

—г+—г I ; (14) д x ²    д у ² )

d и d V ~ --+ — = 0 .

S x   d y

По высоте в сечении канала давление не изменяется, то есть

S P = 0 ^d y

В итоге система уравнений гидродинамики имеет вид:

и д и + V д и = д x     d y	1 д Р я + v p д x	г д2 и  д2 и У. уд x2     d y 2 )	(17)
д V S V V — + и— д т д x	т. д V + V— = v S y	Уд2 т   a 2 V у уд x2    d y 2 )	(18)
	д и  д V 1— д x   д y	0 .	(19)

Уравнений гидродинамики примет вид:

д2и  1 дР v—=--.

д у    p д x

Граничные условия:

U(x, R)=0; U(x, – R)=0.       (21)

Решать данное уравнение будем относительно P=f(x) , т. к. давление изменяется только вдоль канала.

Тогда, учитывая, что р = v • p , имеем:

d2 и dy2 = 1 dР ; р dx (22) аи = 1 ( Sy   р 1 ' дР У |y + C1; , дx ) (23) и = 1 (SP' 2р у дx у ) y2 + C1 y + C2; (24) где С1, C2 – постоянные интегрирования.

Найдем С 1 и С 2 из уравнений (23–24):

1 ( SPA .

и ( x , R ) = — I — I R ² + CR + C   (25)

2р уд x )

1 (SPA .

и ( x , R ) = — I — I R ² + CR + C = 0 ; (26)

2р уд x )

1 Г SPA .

= — I    I R ² - CR + C = 0 ; (27)

2р уд x )

1 ГSPA .

-I — I R ² + 2 C = 0 ;        (28)

руд x )

C 2 =--1 (д Р ) R =;

2р уд x )

-

\ (SPA 1 (SPA

—I —I R ² +—I —I R ² + CR = 0 ; (30) 2 р Уд x )      2 р Уд x )

C 1 =0 .                 (31)

Интегрируя по dx и подставляя значения граничных условий U(x, R)=0, U(x, - R)=0 получим решение данного дифференциального уравнения в виде:

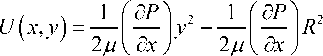
или и (x,R) =    (дР)(R2 - у2);     (33)

2 р уд x )^x       ’

Далее определим расход жидкости через канал как:

R

Q = b J и ( x , R ) =

^{: -} b i R i t" fl P | ( ^{r 2 -} у ²) dy =

^{J - R} 2р уд x )^x        '

= - b_ (a P ^, R ₍R ²- y„dy

2 р уд x )^J- ^{rV        7}

+ R

R² у - y-

- R

b (s p ^ 2 р у a x )

R ³ - — + R³

R ³

Q = -

2 bR ³

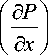
где b высота межмембранного канала.

Рассматриваем дифференциальное уравнение для водопроницаемости с учетом осмотического потока (рисунок 1):

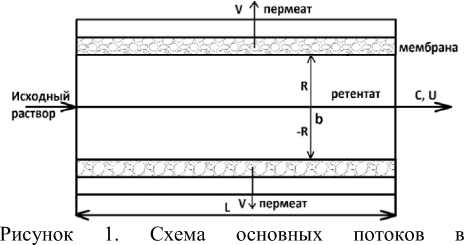
баромембранном процессе

Figure 1. Diagram of the main flows in the baromembrane process

И конечный момент

P ( L ) = Pk(46)

P = C - e0 + С2 - e0 + ш(47)

a

P0 = C + С2 + ш )(48)

a

С2 = P - С - ш(49)

a

P = C - e "L^L + С ₂ - e"' а^L + ^Ш . к 12

a

P = C - e "L^L + | P_o- С , - ^Ш |- e" "L^L

V          a J

P = C - e "L^L + P₀ - e" "L^L -

Тогда

J = к - ( A P -A V_p ) = к - ( P₀ - P ( х ) -A n ) , (37) где J – выходной удельный поток; k – эмпирические коэффициенты; АР - перепад рабочего давления в межмембранном канале до и после мембраны; А V - удельный поток растворителя

. _{C -} е - ^ • ^L - ^ш _е - а ^{- 1 - L} 1 _a

C i =

= P 0

за счет перепада давления до и после мембраны, которые определяются по следующей

зависимости.

A V_p = B - exp( n - A C ) - exp I - I .     (38)

Тогда дифференциальное уравнение для изменения расхода в межмембранном канале

с учетом осмотического потока:

Q x + dx - Q x = dQ = bJdx

Отсюда получаем:

dQ=- ь - j dx

Приравняем уравнения для расходов (36) и (40) получим:

2bR ³ (d P )    , _r

-      I     I = - ь - J

3 ц V d x J

Граничные условия:

AP ( 0 ) = A P o ;

A P ( L ) = A P k ;

Далее, обозначив    3 ц / 2 R ³ = a

и

3 ц J /2 R ³ = ш , получим дифференциальное

уравнение для перепада давления в виде:

^d-^{A P} - aAP + ш = 0         (44)

d x ²

Решение данного дифференциального уравнения в общем виде будет:

P ^>( х ) = C - е ах + С - e- ах'х + ^Ш (45) a

Найдем постоянные интегрирования C и C в начальный P (0) = P

P^. -Po - е"^'L + Ш е"^'L a ера- L - е - 4а-L

P^ -P_o - e "^^{- L} + ^Ш е "^^{- L} a

еЛа-^L - е -^^{- L}

- ^Ш (54) a

Подставим найденные C и C в (45) и по-

лучим выражение для расчета давления по длине канала:

P„ -P„ - е"^L + ^Ше"а"'^L

К 0

P ( х ) =------ г-----^-- е ^^{- х} +

V /            еЛа- L - е- 4а-L

+ P 0 -

P^-Po -е"*-L + ш е"^L a е4а- L - е - 4а- L

>        (55)

^ш - e - * х

a

V                                    J

Подставив найденные значения давления в межмембранном канале в формулы для проницаемости мембран (55), рассчитаем значение продольной составляющей скорости потока.

Подставим найденные значения P = f ( x )

в уравнения для определения продольной (37) и поперечной скоростей (34), обозначив f ( x ) = к - ( A P -A n ) и

f ( x , y ) = ( 2 ц ) ¹ ( d P /d x ) ( R ² - y ² ) , получим сле-

дующую систему уравнений, решением которой является распределение поля концентрации вещества в межмембранном канале:

dC      dC d82c f2 (x, y )^+f (xH- = D^-y    (56)

d x       d y      d y

с ( 0, y ) = С исх ;              (57)

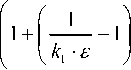
1 - exp J

( ^k 2 —

V   D.-

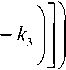
X

C ( x , R ) - ./ , ( x ) = D ^ C I R

k. • e

1            i                   i

1 +--1  1 - exp Jk

( k1 • £ J           (

x

; (59)

,      x , x dC(x,-Л)

x C ( x , - Л ) • f 2 ( x ) = D ⁽_d )

Для проверки адекватности математической мы сравнивали экспериментальные данные с теоретическими результаты экспериментальных данных представлены на рисунке 2.

J-6, m3/m2∙c ф э            ф р            пс э

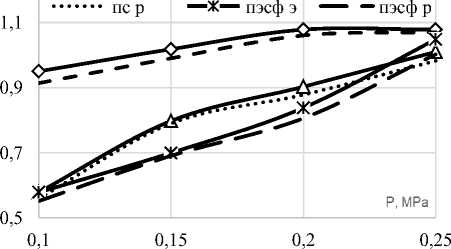
Рисунок 2. Кинетические зависимости выходного удельного потока от трансмембранного давления для ультрафильтрационных мембранам типа БТУ05/2 с материалом активного слоя Фторопласт (Ф), Полисульфон (ПС), Полиэфирсульфон (ПЭСФ)

Figure 2. Kinetic dependences of the output specific flux on the transmembrane pressure for ultrafiltration membranes of BTU05 / 2 type with the material of the active layer Ftoroplast (F), Polysulfon (PS), Polyethersulfone (PESF)

Проверка адекватности предложенной математической модели проводилась средствами имитационного моделирования в PTC Mathcad. Реализующая расчет основных характеристик ультрафильтрационного процесса концентрирования подсырной сыворотки. В PTC Mathcad были заданы параметры и условия ультрафильтрационных процессов, реализованных ранее в лабораторных условиях. Полученные экспериментальные значения выходного удельного потока от трансмембранного давления для ультрафильтрационных мембранам типа БТУ05/2 с мембранами из фторопласта (Ф), полисульфона (ПС) и полиэфирсульфон (ПЭСФ) были сопоставлены с результатами расчета (рисунок 2).

Заключение

Решение математической модели в системе PTC Mathcad показало высокий показатель сходимости, отклонения расчетных данных от экспериментальных не превышало 10% что является оптимальным показателем для инженерных расчетов.

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 20–38–90036.

The reported study was funded by RFBR according to the research project № 20–38–90036.