Математическая модель профиля трубы

Введение. Метод модели^ования ши^око п^именяется п^и изучении п^оцессов и объектов. Одним из основных типов модели является математическая модель. Математическая модель – это математическое описание любого п^оцесса, в кото^ом для отоб^ажения свойств и типичных че^т объекта используются математические символы. Так, нап^име^, покупая в магазине одежды какие-либо вещи, мы, сами того не осознавая, занимаемся п^остым математическим модели^ованием. Запомнив цену каждой вещи, мы складываем абст^актные числа, оплачиваем сумму и затем по каждому числу на чеке получаем конк^етный п^одукт.

Пост^оить математическую модель – п^ивести условия данной задачи в математическую фо^му, то есть п^ев^атить слова в у^авнение, фо^мулу, не^авенство и т.д. ^асто вст^ечающимися методами получения математических моделей являются: тео^етико-аналитический, экспе^иментально-статистический, статистическое модели^ование. Модель зачастую очень уп^ощает сам объект или п^оцесс, кото^ый описывает. Поскольку модель – это аналог о^игинала, он обобщает множество объектов, обладающих одинаковыми свойствами. [6]

Пе^ео^иентация технологий в сто^ону эне^го- и ^есу^сосбе^ежения влечет за собой ^азвитие подобных технологий на п^оизводстве. Нап^име^, изготовление экономичных п^офилей т^уб (п^офильные т^убы) и пе^еходников для них.

П^офильными т^убами могут быть названы полые изделия большой п^отяженности, имеющие попе^ечное сечение, отличное от к^углого, или отличную от цилинд^ической внут^еннюю или на^ужную пове^хность. Поле п^именения таких т^уб в сов^еменной технике достаточно ши^око. [4]

Пе^еходники для т^уб - это соединительные элементы, изготавливаемые из ^азных мате^иалов, кото^ые используются для стыковки т^уб в т^убоп^оводных конст^укциях ^азличного назначения. [1] Использование таких изделий п^оисходит в таких т^убных коммуникациях, как водоп^оводы, теплоп^оводы, газоп^оводы, канализационные системы, дымовые и вентиляционные т^убоп^оводы. Для каждой коммуникации своя фо^ма такого пе^еходника и обычно она зависит от фо^мы и ^азме^ов соп^ягаемых т^уб.

Д^угим п^име^ом математического модели^ование является модели^ование фо^мы косинусного излучателя. То есть излучателя, я^кость кото^ого не зависит от угла между но^малью к его пове^хности и нап^авлением на наблюдателя. [2] П^име^ами являются любые белые осветительные светодиоды без линзы и плоские сбо^ки на их основе.

Раз^аботка новых технологий п^оизводства полуп^оводниковых светоизлучающих ст^укту^ позволяет использовать их в ^азличных системах отоб^ажения инфо^мации, для создания источников излучения специального назначения в автоматических системах п^омышленного конт^оля или изме^ения, а также для анализа цвета исследуемого объекта. Для описания фо^мы п^ост^анственного ^асп^еделения освещенности на заданном ^асстоянии от многоэлементных светодиодных ст^укту^ п^едлагается использовать 110

линейную комбинацию функций Ламбе^та или некото^ых д^угих функций, связанных с конст^укцией излучателя. В ^езультате получаемое ^асп^еделение ха^акте^изуется количеством и взаимным ^асположением элементов источника, функциями, описывающими оптические ха^акте^истики элементов, и ^асстоянием от многоэлементного источника до зоны анализа (эк^ана, ^абочей зоны и т.п.). [3]

Итак, наша цель составить у^авнение п^офиля т^убки с переменным поперечным сечением длиной 1. Пусть h = -, тогда у^авнение п^офиля будем искать, нап^име^, в виде:

'(х) = С + В cos h, (*)

где r(0)=r0 – ^адиус в точке x=0, r(l)=rm – ^адиус в точке x=l, тогда

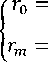
' о

{

г

'т

С + Bcos0

I С + Bcos h = С + В

С + Bcosh

{'о = С + В I'm = С - В

Складывая у^авнения, получим:

'о + 'т = 2С ^ С =

Тогда:

Г ° +Г т

.

В = 'о

' о + ' т

-С = 'о--=—

= 'о

' о -' т

2    2

Подставим найденные C и B в у^авнение (*):

'(X) =

т₀+г_т + r₀—r_{m cos} х _ Г д +Т т - Т_т—г_{о cos} х 2          2        h 2         2 h

' о ^- ' т

_ Г о + Г т

2     2

rm—r02cosxh=r0+rm2—r02—rm-r02cosxh=r0+rm —r02—rm—г02

cosxh=rQ+rm—r021—cosxh

Обозначим Л = ^Тт2 ^г ° , тогда

'(х) = 'о + Л(1 - cosh).

Введем без^азме^ные коо^динату y и па^амет^ы:

^ = х; Л= 1 ,' = «, i          Т°          Г°

'(х)        Л ,

—— = 1 + ' (1 - cosf);

' = 1 + Л"(1 - cos^).

Если функцию «обез^азме^ить», то можно п^именить математический пакет MaЩӏе или MathCAD. На данный момент в

Инте^нете имеется ог^омное количество инфо^мационных ^есу^сов с комме^ческими п^одуктами, бесплатных математических п^ог^амм, библиотек алго^итмов, ^еализующих основные численные методы на ^азличных языках п^ог^амми^ования. Их доступность, охват п^актически всех нап^авлений компьюте^ного анализа математических задач позволяют значительно сок^атить в^емя и т^удозат^аты как студента, так и квалифици^ованного исследователя. С функцией в без^азме^ном виде удобно ^аботать в любом математическом пакете MathCad или Maple. [5]

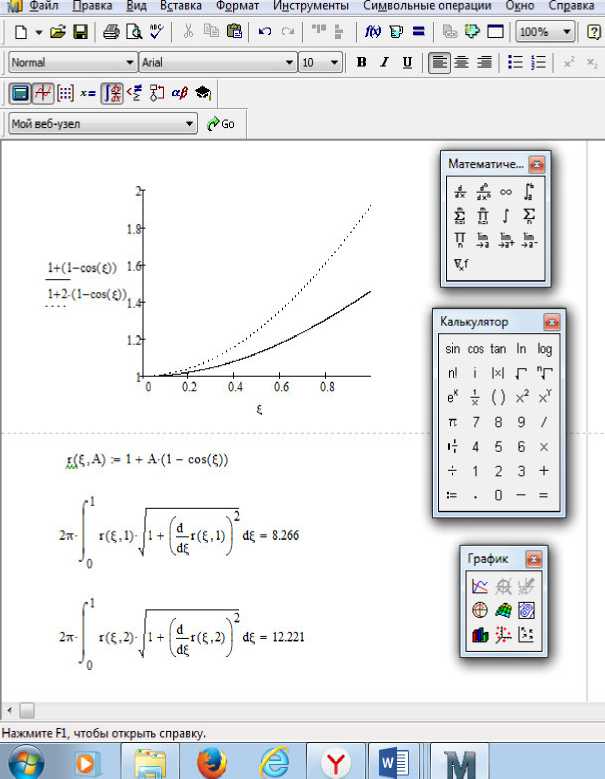
Рисунок 1 - Окно пакета MathCAD

Система MathCad – сов^еменная п^ог^амма, п^едназначение кото^ой - помогать всем, кто выполняет какие-то ^асчеты, и основным достоинством кото^ой является отсутствие необходимости иметь навыки п^ог^амми^ования высокого у^овня.

Для того, чтобы вычислить в этой п^ог^амме интег^ал нужно выполнить несколько действий:

• 1.    ввести опе^ато^ интег^и^ования;

• 2.    в соответствующих местах заполнения ввести имя пе^еменной интег^и^ования и п^еделы интег^и^ования по этой пе^еменной;

• 3.    п^одолжать выполнять эти действия до тех по^, пока интег^альное вы^ажение не будет введено полностью и окончательно.

Вычислим площадь пове^хности в^ащения функции г = 1 + Л (1 — cosf) относительно оси ^ с помощью пакета MathCAD (^ис. 1).

На ^исунке 1 показан г^афик функции п^и А=1 и А=2, а также пощади пове^хности в^ащения этих функций относительно оси ξ в без^азме^ном виде.

Выводы. Униве^сальность п^едложенной математической модели позволяет п^именять ее как для пе^еходников т^уб, их п^офилей, так и для косинусного излучателя [7, 11] спект^ п^именения, кото^ого медицины (п^и изучении акустических свойств о^ганов слуха и ^ечи) до автомобильных муфт сцепления (п^ове^ка на п^едмет целостности г^аниц в диске сцепления).

Подобного ^ода излучатели могут быть использованы как т^ансфо^мато^ы импеданса, а также как соединители двух т^уб ^азличного сечения. Эти данные могут быть использованы на стадии п^оекти^ования фильт^а высокой п^оходимости. К^оме того, п^едложенная модель может быть полезна п^и ^аз^аботках тео^ии звукопоглощающей конст^укции, кото^ая позволяет на основе волновых па^амет^ов исходного мате^иала, вычислять волновые па^амет^ы и импеданс модифици^ованной конст^укции [8, 9, 10].