Математическая модель прогнозирования остаточного ресурса изоляции по режимным параметрам

Общеизвестно, что изоляционные материалы имеют широкий диапазон применения в различных конструкциях. При этом замена конструкций с истекшим нормативным сроком эксплуатации в течение короткого промежутка времени бывает невозможна из-за больших капитальных затрат, поэтому перед эксплуатирующими организациями неизбежно возникает вопрос об оценке остаточного ресурса изоляции. В настоящий момент ведутся исследования в области разработки материалов с большим сроком эксплуатации, а также позволяющих восстанавливать свои электрические свойства [1].

Фактические электрические свойства материалов зависят от предрасположенности к накоплению и развитию дефектов под действием режимных параметров [2, 3], таких как температура, повышенное напряжение, коммутационные перенапряжения и др., которые оказывают значительное влияние на электрическую прочность изоляции. В случае изоляции кабеля воздействие вышеприведенных факторов при длительной эксплуатации оказывает существенное влияние. В [4] показано, что, например, значения перенапряжений могут меняться в зависимости от структуры самой сети, то есть при наличии неоднородностей в схеме [4, 5]. Таким образом, возникают вопросы по оценке остаточного ресурса как кабельной линии (КЛ) во время эксплуатации, так и при разработке новых схемных решений и новых изоляционных материалов.

Существует большое количество неразрушающих методов оценки состояния изоляции. Контроль технического состояния изоляции можно провести при помощи измерения сопротивления, ёмкости, угла диэлектрических потерь tgδ, метода рефлектометрии, тепловезионным способом и т. д [6–10]. В последнее время все больше внимания уделяется методике с использованием частичных разрядов (ЧР) [6–11], при помощи которой можно проводить диагностику для силовых, измерительных трансформаторов, электрических машин, КЛ и прочего электротехнического оборудования.

В научной литературе обсуждалось и сравнивалось [8–10, 12] несколько теоретических и математических моделей для оценки остаточного ресурса изоляции. Однако наибольшую известность получила модель Кучинского [13], поскольку она включает в себя энергетические показатели, такие как мощность ЧР и температуру, определяемые экспериментально.

Использование модели Кучинского носит не совсем полный характер. В работе [8] при определении остаточного ресурса кабеля использовались не только экспериментальные данные, но и информация о нормативном сроке службы кабеля, при отсутствии которой остаточный ресурс получился завышенным в несколько раз. В работе [9] срок службы был определен в относительных единицах и с использованием рекомендованных ком- панией Emerson Electric уровней мощности ЧР для конкретного вида изоляции [14].

Определение остаточного ресурса в относительных единицах не всегда удобно для эксплуатирующих предприятий и малоинформативно при анализе новых схемных решений и новых видов изоляции, в том числе из самовосстанавливающих-ся материалов [1]. В этих исследованиях актуальность приобретают вопросы об остаточном ресурсе и его изменении под влиянием различных факторов, скорости старения под действием различных механизмов, точности полученных результатов и т. д. Поэтому целью настоящей работы является получение метода обработки экспериментальных данных в рамках модели Кучинского, позволяющей ответить на поставленные выше вопросы.

Математическая модель и описание метода оценки остаточного ресурса изоляции

Согласно предложенной математической модели остаточный ресурс можно представить в виде B 1

• R ( UTn ) = fAn e^T-           (1)

где n - номер опыта; f ) ( U , n ) - мощность ЧР, полученная в n -м опыте; T – температура; А ₁ и В ₁ – коэффициенты, подлежащие определению.

При этом единичной удобнее считать мощность ЧР нового образца, наблюдаемую при номинальном напряжении U _н. Классическая модель Кучинского имеет вид

W a

• т _ст = A ■ E-ⁿ ■ e k ^T ,                              (2)

где A – постоянная, зависящая от материала и свойств изоляции; E – напряженность электрического поля; n – индекс степени, зависящий от типа изоляции; k – постоянная Больцмана; W _a – энергия активации; T – температура.

В (2) сомножитель перед экспонентой имеет вид A ■ E ^- n , что усложняет модель, поскольку напряженность поля в дефекте необходимо рассчитать, а для этого нужна информация о геометрических размерах дефекта. Дополнительно к этому функция E ^{- n} по сути является аппроксимацией зависимости мощности ЧР от приложенного напряжения, и эта аппроксимация при дальнейших расчетах приведет только к дополнительной систематической ошибке. Кроме того, в (2) присутствует энергия активации W _a , определение которой часто вызывает сложности.

Однако выбор в качестве аргумента функции (1) мощности ЧР в относительных единицах тоже имеет свои недостатки. При некоторой критической величине напряжения U к _р <  U _н ЧР отсутствуют, и в модели будет деление на ноль. Устранить данное несоответствие можно введением фиктивной мощности ЧР при малых напряжениях, чтобы сохраня-

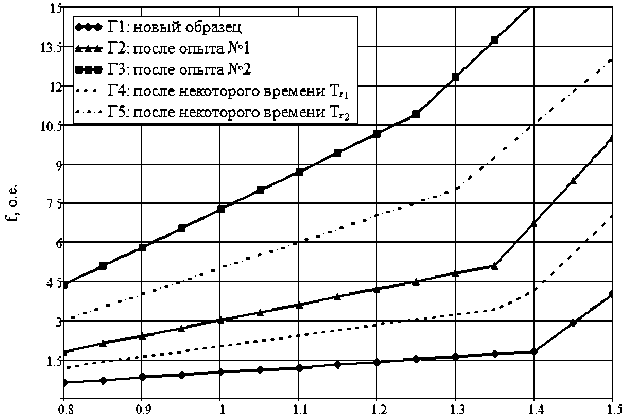
Рис. 1. Зависимость мощности ЧР от приложенного напряжения

Fig. 1. Dependence of the partial discharges intensity (PDI) on the testing voltage

лась непрерывность функций. Малыми напряжениями в данном случае можно считать напряжения U кр <  0,8 U _н, так как эксплуатация системы электроснабжения при таких напряжениях недопустима согласно [15]. Введение фиктивной мощности ЧР приведет к тому, что модель будет справедлива только в области напряжений более 0,8 U _н .

Модель (1) применима только в области медленного старения изоляции (порядка суток и более). Поэтому существует верхняя граница применимости модели по напряжению, которая определяется приблизительно 90 % от напряжения пробоя U _пр , так как пробой диэлектрика носит стохастический характер [9, 16]. Аналогично существует и верхняя граница применимости модели по температуре, выше которой наблюдается быстрое термическое разрушение образца. С учетом этих ограничений сформулируем необходимые исходные данные.

• 1.    Зависимость мощности ЧР от напряжения f ( U ,0 ) на новом образце (график Г1, рис. 1).

• 2.    Условия проведения 1-го опыта старения: t ₁ – время, T ₁ – температура, U ₁ – напряжение.

• 3.1.    Зависимость мощности ЧР от напряжения f ( U ,1 ) после 1-го опыта старения образца (график Г2, рис. 1).

• 3.2.    Зависимость мощности ЧР от напряжения f ( U ,1 ) через некоторое время T_r1 (график Г4, рис. 1).

• 4. Условия проведения 2-го опыта старения: t ₂ – время, T ₂ – температура, U ₂ – напряжение.

• 5.1.    Зависимость мощности ЧР от напряжения f ( U ,2 ) после 2-го опыта старения образца (график Г3, рис. 1).

• 5.2.    Зависимость мощности ЧР от напряжения f ( U ,2 ) через некоторое время T_{r 2} (график Г5, рис. 1).

Приблизительный вид функций f (U, 0), f (U,1), f’(U,1), f (U,2), f'(U,2) показан на рис. 1. Под Tr.n подразумевается время, необходимое для восстановления диэлектрических свойств материала после n-го опыта старения образца. За базовое значение напряжения взято номинальное Uн , при котором эксплуатируется оборудование. За базовую величину мощности ЧР принята мощность ЧР, измеренная для нового образца при номинальном напряжении f (Uн,0). Характерный вид графиков соответствует экспериментальным данным, приводимым в литературе [17].

В расчётах старения приняты значения:

• t, = 400 ч, U = 1,25 U_H , Т = 1,242 Т , t ₂ = 400 ч, 1          1      н 1       н2

U 1 = 1,25 U н , Т 1 = 1,182 Т н . Например, для кабеля, согласно [18], исходные данные соответствуют условиям проведения экспериментов по старению электротехнических образцов. Для получения двух параметров, характеризующих материал, нужно составить два уравнения из имеющихся данных:

/ R ( u 1 , т 1.0 ) - R ( u 1 , т 1.1 ) = t 1 ;

\ R ( U 2 , T 21 ) — R ( U 2 , T 2.1 ) = 1 2 .

Каждое уравнение из системы уравнений (3) показывает разность между ресурсом до опыта старения и после опыта старения в конкретных условиях, при которых выполняется старение. Проведя несложные, но объемные вычисления, можно получить выражение для оставшегося ресурса только через опытные данные:

R ( и , T , n )

K ( T ) [ F 2 ■ F 1 k ^{( T} ) f ( U , n )\ F 2 - F i J

( V        ^k ( ^T ) — 1

(

где f ( U , n ) - относительная мощность ЧР, полученная в опыте n и зависящая от напряжения U , при котором предполагается эксплуатация образца, о. е.; F 2 = f ( U 2 ,2 ) , F 1 = f ( U ₂,1 ) - относительная мощность ЧР в конце и в начале второго опыта старения при напряжении U ₂ , при котором выполняется 2-й опыт, о.е.; F i = f ( U i ,1 ) , F o = f ( U ,0 ) - относительная мощность ЧР в конце и в начале 1-го опыта старения при напряжении U ₁ , при котором выполняется 1-й опыт, о. е.

Коэффициенты, зависящие от температуры Т , при которой предполагается эксплуатация образца, можно определить по выражениям:

( t 1 k ( T )

к ( t ) = ti       I ;(5)

V t i )

, . T-T k (T) = T2 ■ Ц.

v ’ 2 T (T2 - T1)

Таким образом, выражение (4) позволяет определить остаточный ресурс в момент проведения n -го опыта с ЧР, т. е. для частично состаренного образца. Анализ выражений после (5), (6) показывает некоторые ограничения на проведение опытов:

• –    опыты старения должны быть выполнены при разных температурах, иначе в выражении (1) будет невозможно восстановить коэффициент В 1 ;

• –    опыты с ЧР должны быть выполнены как минимум до величины напряжений, при которых выполняются опыты старения образцов.

Графики зависимости ресурса (4) от эксплуатационного напряжения показаны на рис. 2: для нового образца (Г1), для образца после 1-го и 2-го опытов старения без учёта времени релаксации (Г2 и Г3) и с учётом времени релаксации (Г4 и Г5). Ожидаемый ресурс нового образца при номинальном напряжении – чуть больше 30 лет, что соответствует данным анализа эксплуатации кабелей [9]. Следовательно, выбранные параметры эксперимента соответствуют реальной ситуации. Резкое уменьшение срока службы на графиках соответствует увеличению ЧР в опытах, что является одним из сигналов к более тщательному мониторингу за состоянием изоляции, а при достижении критических значений или близких к нему – принятия необходимых мер.

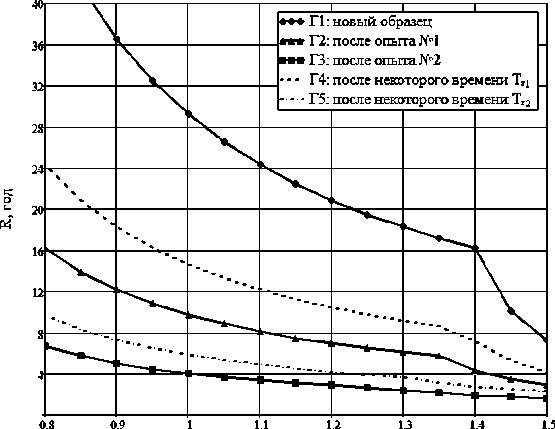
U: o.e.

Рис. 2. Зависимость срока службы от приложенного напряжения Fig. 2. Dependence of the residual life of the sample on the testing voltage

Для любого косвенного измерения крайне важным является вопрос о точности этих измерений. При проведении лабораторных исследований условия старения (время, температуру, напряжение) можно считать измеренными точно. Основная ошибка будет допущена при измерении мощности ЧР, так как их мощность определяется случайными процессами как при их возникновении, так и при гашении [16]. Поэтому для оценки остаточного ресурса будем считать, что мощность ЧР измерена с относительной погрешностью df . Величина этой погрешности при существующих методиках проведения измерений ЧР может составлять около df = 5 % .

По общепринятой методике обработки результатов косвенных измерений [19] ошибка косвенного измерения от результатов 5 опытов по ЧР:

dR =

Г 177  \2  < _ л2  / _ \2 77 \2    _)

Г д R ]   I д R ]   Г д R ] Г д R ]    (9 R Y

\[д F 0 ) ⁺ly F ^{J       J      J +}U f 7

V                                                  7

■ df ,

где д R /д F _o , д R /д F i' , д R /д F_i , д R /д F 2 , д R /д F – частные производные остаточного ресурса по мощности ЧР, определенной соответственно:

• 1)    при U ₁ до 1-го опыта старения;

• 2)    U ₁ после 1-го опыта старения;

• 3)    U ₂ до 2-го опыта старения;

• 4)    U ₂ после 2-го опыта старения;

• 5)    предполагаемых значениях эксплуатационного напряжения U .

Указанные производные соответственно равны:

д R _   к ■ F ₂     _   д R _   к ■ F i      _   д R _ ( к - 1 ) - F o

----- =  7---------Г ■ R ;  Г = ----7---------Г ■ R ; ---- = ----7---------Г ■ R ;

д F o   F i ( F 2 - F i )      д F   F ( F 2 - F i )      д F i f;( F - F o )

R R = ( к - 1 ) -   /i   _V R ;    = —R- R .

д F 2 ⁽    ) F o ( F i' - F o )       д F f o ■ U

Оценка относительной погрешности ресурса (4) при параметрах опытов: t_i = 4oo ч, U _i = i,25 U _н, Т _i = i,242 T _н , 1 ₂ = 4oo ч, U _i = i,25 U _н, Т _i = i,i82 T _н составляет 2i % (для нового образца) при эксплуатации при номинальном напряжении. Достаточно высокие значения погрешности могут быть вызваны произвольным выбором «экспериментальных данных о ЧР», не учитывающих постепенное, а не пороговое возрастание нелинейности, а также несогласованность этих данных с параметрами старения.

Аналогичный расчет, выполненный при параметрах ti = 5,7o8 года, Ui = i,o5Uн, Тi = i,o3Tн, 12 = 5,7o8 года, Ui = Uн , Тi = Тн, близких к условиям эксплуатации, показал погрешность 5,8 %. Однако при условиях эксплуатации дополнительную погрешность будет вносить неопределенность в температуре, при которой осуществляется эксплуатация. Величина относительной погрешности в определении ресурса при ошибке в параметре к (T) может быть оценена по формуле дR

5Fq

Г -FlFl

V F i - F 2

F 0

-

F i' l

к - i

F o - F i' ^J

■ In

Г -FlFl

V F i - F 2

F o - F i F o - F i ^J

В случае, когда относительная ошибка в определении параметра к ( T ) составляет 5 %, общая ошибка в определении ресурса будет 8,1 %.

Обсуждение и практическое применение

На текущий момент ЧР являются общепризнанным индикатором, позволяющим оценить текущее состояние изоляционных материалов [6–11, 13, 14]. Поэтому распространение данного подхода и предлагаемого метода для оценки самовосстанавливающихся материалов выглядит обоснованным. Преимуществом предлагаемого метода по сравнению с другими является возможность оценки остаточного ресурса изоляции в динамике.

Старение изоляции вызвано многими факторами, среди которых длительное влияние электрического и теплового поля, химическое влияние агрессивных веществ, увлажнение, снижающие изоляционные характеристики диэлектрика, механические воздействия и т. д. [10, 13, 20]. В выражении (1) мощность ЧР характеризует состояние материала в данный момент. Поэтому в данном выражении можно учитывать и другие виды старения, для этого в (1) необходимо вводить дополнительные сомножители, а в (2) необходимо добавить ещё один опыт старения. Сами же опыты нужно проводить с различными значениями факторов аналогично тому, как в рассмотренной работе температуры старения должны быть различными.

Предложенный в статье метод можно также применить для проверки и испытания КЛ классов напряжения 6 и 10 кВ электрохозяйства ПАО «Россети», которые на текущий момент проводятся в соответствии со стандартом организации [21]. Согласно ему оценочным критерием успешности проведения испытания является пробой либо перекрытие по поверхности. В случае несоблюдения одного из этих факторов считается, что изоляция электрического испытания не выдержала. Метод испытания повышенным напряжением предполагает лишь качественную оценку состояния изоляции относительно приложенного напряжения, обеспечивающего некоторый коэффициент надежности. Какой-либо возможности прогнозирования остаточного срока службы КЛ используемый на данный момент метод не имеет.

Как видно из ежегодно публикуемой статистики о технологических нарушениях [22], для линий с высокой степенью аварийности подобное испытание является разрушающим, практически выявляющим место КЛ с наименьшей электрической прочностью. С учетом невозможности оценки остаточного ресурса КЛ в условиях электрохозяйства с высокой степенью износа кабельной инфраструктуры могут иметь место отклонения от приведенного метода с целью недопущения выхода испытываемой линии из строя.

Исследования ЧР в КЛ, равно как и методов контроля состояния КЛ, ведутся в течение продолжительного времени [6, 13, 23]. Предложенный метод потенциально позволяет спрогнозировать ухудшение изоляционных свойств кабеля и, следовательно, дать оценку остаточного срока службы. Оценку предполагается проводить по результатам испытаний образцов реальной линии, полученной в ходе специального отбора либо по результатам ремонтных работ. Помимо этого, предложенный метод потенциально позволяет оценить влияние на КЛ различных дополнительных факторов (коммутационные перенапряжения, электротермическое и электроди-

намическое воздействие токов короткого замыкания и т. д.), что является предметом дальнейших исследований.

Описанный в статье метод достаточно легко воспроизводится в лабораторных условиях. Воздействующими факторами метода являются время, напряжение и температура, которые легко воссоздать с достаточной точностью и повторяемостью. Способ измерения кажущегося заряда ЧР также является стандартным, применяя который легко определить мощность ЧР. На основе предложенного подхода потенциально возможно создать стандартный метод оценки старения изоляции электротехнических устройств.

Предложенный метод может иметь большую практическую пользу с точки зрения оценки ожидаемой либо остающейся надежности, планирования сроков ремонтных работ, формирования бюджета ремонта и модернизации системы КЛ, разработки мероприятий по увеличению их срока эксплуатации.

Вывод

В работе предложен алгоритм по оценке остаточного ресурса изоляции на основе модели Кучинского. Предложенная математическая модель позволяет использовать только параметры, которые можно получить в ходе эксперимента (температура, напряжение, мощность ЧР) и отказаться от расчетных величин, таких как мощность активации, напряженность локального электрического поля, геометрических размеров дефекта в изоляции или иных трудноопределяемых параметров. Данная модель позволяет оценить погрешность определения остаточного ресурса в зависимости от погрешностей экспериментальных данных и обладает вариативностью в использовании факторов, воздействующих на процесс старения изоляции, что расширяет её возможности, кроме того, модель позволяет производить оценку остаточного ресурса как обычных, так и самовосстанавливающихся материалов.