Математическая модель распространения дыхательных шумов в респираторном тракте

Понимание физических процессов в воздушных путях легкого, различие процессов у здоровых и пациентов, страдающих различными легочными заболеваниями (астма, муковисцидоз, респираторные инфекции и т.д.), и причин, вызывающих эти различия, в значительной степени может облегчить определение критериев компьютерной диагностики, основанной на анализе дыхательных шумов.

Различные дыхательные шумы в разных областях бронхиального дерева легких связаны с разными типами течения воздуха в воздушных путях: ламинарный, переходный, турбулентный [ 1 ] . Любая генерация звука в каналах с потоком газа вызывается нелинейными механическими эффектами в самом потоке или/и при взаимодействии потока с границами канала. При этом часть энергии потока преобразуется в возмущения потока и давления. Легочные заболевания вызывают изменения воздушных путей, что приводит к появлению дополнительных шумов. Обзор механизмов возникновения дыхательных шумов приведен в [3].

Математическое моделирование возникновения и распространения дыхательных шумов в легких можно разделить на две части: моделирование анатомической структуры воздушных путей и моделирование их функционирования, физических процессов, протекающих в воздушных путях и связанных с течением воздуха.

В литературе приводятся различные подходы к математическому моделированию физиологии воздухоносных путей легких [1, 3, 4, 9–11, 14, 18, 19, 21– 24, 26, 32, 33]. Здесь отметим некоторые из них.

Kitaoka с соавт. [ 19 ] разработали трехмерную (3 D ) модель дыхательных путей человека от трахеи до терминальных бронхиол, используя алгоритм, анализирующий ветвление бронхов и распределение воздухоносного пространства. Алгоритм относительно прост и дает реалистичные результаты, отражающие бронхиальное дерево с морфометрическими характеристиками, которые оказались очень близки к анатомическим данным. Алгоритм предлагает новую методологию для более детального понимания структурно-функциональных связей трахеобронхиального дерева и позволяет осуществлять 3 D- моделирование, основанное на рассмотрении взаимодействий воздухоносных путей и паренхимы легких.

Schmidt и соавт. [ 26 ] предложили цифровую эталонную модель бронхиального дерева нормального легкого, основанную на изображениях легких, полученных с помощью компьютерной томографии высокого разрешения. Данные изображения использовались для углубленного компьютерного исследования ветвления бронхиального дерева и статистического анализа его объемного строения.

Авторы работы [ 21 ] моделировали бифуркационные потоки воздуха в ассиметричных воздухоносных путях легкого человека.

По данным Ma и Lutchen [22] импеданс легких на вдохе, измеренный с помощью вынужденных колебаний в низкочастотном диапазоне, оказался чувствительным показателем к тяжести заболевания и степени неоднородности его распределения в легких. В этом исследовании авторы выдвинули основанную на результатах компьютерных томографий мультимасштабную модель человеческого легкого, которая включает в себя верхние и центральные дыхательные пути, мелкие дыхательные пути и часть альвеолярной ткани. При построении своей модели авторы комбинировали 3D-модель верхних дыхательных путей (реконструкция данных магнитно-резонансной томографии) с 3D-моделью центральных дыхательных путей (на основе мультиспиральной компьютерной томографии) от входа в гортань до 6-й генерации. Моделирование на уровне мелких дыхательных путей дистальнее центральных ветвей трахеобронхиального дерева было основано на гипотетическом дереве дыхательных путей для нормального здорового легкого. Для блока альвеолярной ткани предполагалась однородная фазовая вязкоупругая модель. Используя численные методы гидродинамики, моделировались нестационарные воздушные потоки в больших дыхательных путях. Экспериментальное измерение потока при форсированном дыхании проводилось во рту. Импеданс малых дыхательных путей был рассчитан на основе одномерной линейной модели. Вычисленные общая динамическая устойчивость и эластичность легких очень хорошо соответствовали экспериментальным значениям. Результаты показали, что нестационарное 3D-моделирование и рассмотрение реалистичной модели строения верхних и крупных дыхательных путей до 4–6-й генерации могут обеспечить достаточно точную оценку импеданса легкого на вдохе. Сопротивление верхних дыхательных путей составляет значительную часть полного инспираторного импеданса легкого. Сопротивление верхних дыхательных путей занимает 45–70% от общего сопротивления легких на частотах от 0 до 1 Гц и 70–81% на частотах от 1 до 8 Гц. В работе Cebral [10] показано, как результаты виртуальной бронхоскопии могут быть использованы при выполнении аэродинамических расчетов в анатомически реалистичных моделях.

Ozer с соавт. [ 24 ] в своих исследованиях использовали модель граничных элементов ( Boundary Element Model ) для моделирования распространения звука в паренхиме легких. Результаты математического моделирования сравнивались с экспериментальными исследованиями на фантомных моделях легкого человека. Исследователи количественно оценили влияние различных параметров в модели на получающееся акустическое поле в фантомах легких. Затем в модели граничных элементов применялся алгоритм локализации для прогнозирования положения акустического источника в фантоме.

В [ 11 ] была разработана комплексная модель передачи звука через легкое свиней и проведена экспериментальная оценка точности моделирования. В разработанной «предметной» модели используются характеристики паренхиматозной части легкого и заложена архитектура крупных дыхательных путей, определенная из изображений компьютерной томограммы легких. Модель также использовалась для вычисления и визуализации виброакустического давления и движения внутрилегочных дыхательных путей под воздействием входного акустического сигнала. В работе моделировался акустический отклик при диффузном фиброзе легких и опухоли легкого.

Отдельным направлением математического моделирования является изучение генерации и распространения дыхательных шумов в верхних отделах дыхательных путей [ 33 ] .

Ряд работ [17, 18] посвящен математическому моделированию дыхательных шумов в здоровых легких и звукообразования, базирующемуся на аналоговом подходе. В этих работах процессы в дыхательных путях моделировались процессами в линейных электрических цепях.

В настоящей статье авторы моделируют изменения в амплитудно-частотной характеристике дыхательных шумов, вызванные астматическим заболеванием. При моделировании учитываются анатомические изменения, вызванные заболеванием, и аналоговый подход используется для расчета шумов, возникающих в респираторном тракте.

Методы и организация исследования

Моделирование анатомической структуры воздушных путей

С точки зрения математического моделирования, воздушные пути представляют собой ветвящуюся систему трубок различных длин и диаметров. Трубки моделируют трахею, бронхи, бронхиолы, терминальные бронхиолы, альвеолярные ходы. Толщина стенок и их эластичные свойства зависят от размеров трубок и их расположения, а также от состояния здоровья. Альвеолярные мешочки моделируются источниками изменения давления: при выдохе давление в них выше атмосферного; при вдохе – ниже. Анатомически, начиная с трахеи, трубки разделяются на каждом уровне на две (рис. 1) [2]. Общепринятая схема ветвления Вейбеля содержит 23 уровня ветвления. Однако при математическом моделировании часто рассматривают меньше уровней ветвления: при моделировании нарушений течения воздуха, вызванных астмой, учитывается 12 уровней [32]; в [18] в акустической модели респираторного тракта – 10. В [17] при моделировании дыхательных шумов предложено рассматривать 35 уровней, что позволяет учитывать микроструктуру легкого. В [17] приведены средние размеры трубок и их характеристики (вязкость, упругость и т.д.) взрослого здорового человека. У больных эти размеры, особенно толщина стенок, могут значительно меняться. При моделировании ряда заболеваний необходимо также учитывать появление жидкости в воздушных путях. У детей размеры и эластичность трубок сильно зависят от возраста.

При простом моделировании можно предполагать, что каждая трубка ветвится на две одинаковые на следующем уровне. Более точное моделирование должно учитывать несимметрию ветвления [17, 18]. Несимметрия ветвления проявляется при частотах выше 2000 Гц, и его влияние на амплитудно-частотную характеристику растет с частотой [12]. Астматические изменения в легких вызывают характерные дыхательные шумы, основная частота которых лежит между 100 и 1000 Гц [28] и между 400 и 1600 Гц [29].

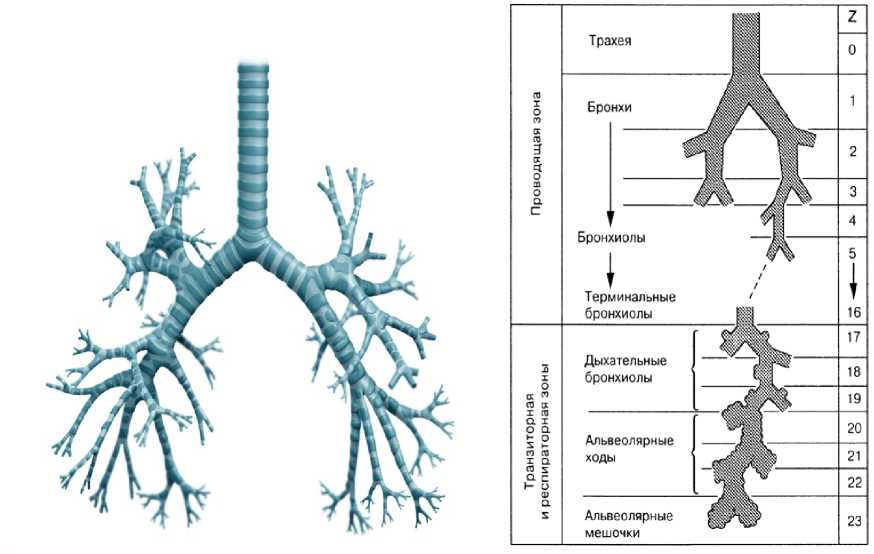
б

а

Рис. 1. Схема дихотомического ветвления путей Вейбеля с числом ветвлений 23: а – трахеобронхиальное дерево; б – разделение воздушных путей на уровни [2]

Ниже при моделировании вляния астматических изменений на амплитудночастотную характеристику дыхательных шумов мы будем использовать симметричную 35-уровневую модель.

Моделирование воздушных потоков

В зависимости от размеров трубки, их соотношений, скорости течения воздуха в трубке может реализоваться один из трех типов течения воздуха: ламинарный, переходний или турбулентный. При изменении во времени скорости воздушного потока характер течения также может меняться, более того, он может меняться вдоль достаточно протяженной трубки даже при постоянной скорости течения. Точное решение газодинамической задачи связано с решением нестационарных дифференциальных уравнений в частных производных одновременно для всей системы. Решение усложняется необходимостью учета эластичности стенок трубок. Для преодоления этих трудностей при анализе дыхательных шумов предлагается воспользоваться аналоговым моделированием, при котором рассмотрение воздушных потоков заменяется рассмотрением электрических процессов:

• •    каждая трубка замещается электрической цепью;

• •    падение давление на трубке эквивалентно падению напряжения в цепи;

• •    воздушный поток – электрическим током.

В электрической цепи (рис. 2) емкость C a и индуктивность L a моделируют сжимаемость и инерцию воздуха соответственно [17, 18]. Сопротивление R a и проводимость G a характеризируют потери, вызванные вязкостью воздуха и его нагревом; L wc , C wc , R wc моделируют свойства хрящей и L ws , C ws , R ws – мягких тканей. Введение в электрическую цепь двух ветвей R wc –L wc –C wc и R ws –L ws –C ws позволяет моделировать неоднородность свойств стенок по длине, например, стенки трахей содержат мягкие ткани, перемежающиеся хрящевидными кольцами. Изменение неоднородности стенок от трубки к трубке моделируется изменением относительного содержания хрящевой ткани. Каждый структурно-функциональный элемент респираторного тракта представлен в виде эквивалентной электрической цепи, параметры (величины сопротивлений, емкостей, индуктивностей) которой определяются его анатомическим расположением – номером уровня ветвления.

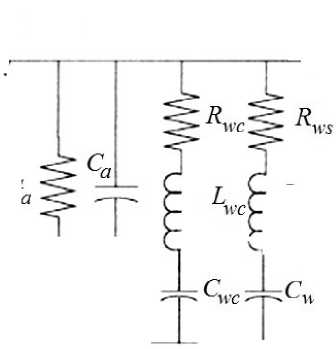
Рис. 2. Электрическая схема, эквивалентная одной трубке [29]. Описание элементов схемы см. в тексте

Расчет параметров эквивалентной схемы (см. рис. 2) осуществлялся с использованием выражений, приведенных в [17]: уравнения (1) и уравнения в табл. 1 и 3. Характеристики воздуха и мягких и хрящевидных тканей респираторного тракта приведены в табл. 2 и 4 в [17], размеры трубок (длина, радиус, толщина стенок), а также относительное содержание хрящевидной ткани в зависимости от генерации для взрослого человека – в табл. 5. Размеры и характеристики элементов дыхательных путей (трубок) данной генерации не зависят от их месторасположения в легком, и, следовательно, необходимо определить параметры только 35 элементов эквивалентной схемы.

R a и G a зависят от частоты, однако все параметры электрической цепи не зависят от тока и приложенного напряжения. Это позволяет использовать методы, разработанные для расчета токов и напряжений в линейных электрических цепях. В [17] обсуждается применимость предположения о независимости параметров цепи от интенсивности воздушного потока и показано, что такое приближение работает достаточно хорошо в широком диапазоне интенсивностей.

Электрическая схема каждой трубки (см. рис. 2) может быть представлена как пассивный четырехполюсник, а точка ветвления как параллельно-последовательное соединение четырехполюсников (рис. 3). Таким образом, все легкое представляется набором параллельно-последовательно соединенных четырехполюсников, а альвеолы представлены как источники напряжения. Наибольшее количество четырехполюсников соединено с источниками напряжения и уменьшается в два раза с переходом на следую еолах одинаково: напряж

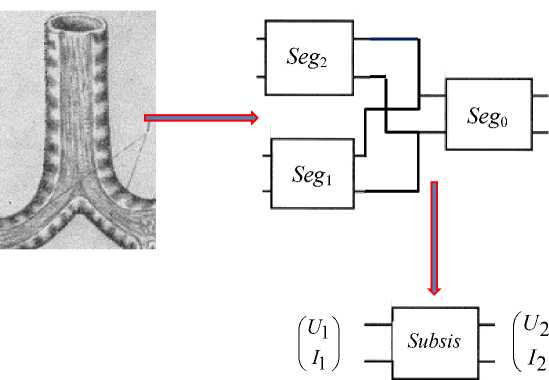
Рис. 3. Представление ветвления как параллельно-последовательного соединения четырехполюсников и их преобразование в один; напряжение U 1 и ток I 1 на входе и U ₂, I ₂ на выходе из четырехполюсника. Seg – сегмент ветви

Используя правила преобразования электрических цепей при расчете токов и напряжений [17], начиная с ближайших к источникам напряжения четырехполюсников, их параллельно-последовательное соединение преобразуется в один четырехполюсник. Во-первых, два параллельных четырехполюсника преобразуются в один: точка ветления представляется как два последовательно соединенных четырехполюсника. На следующем шаге эти два последовательно соединенных четырехполюсника преобразуются в один. В результате два уровня (две генерации) преобразуются в один эквивалентный. Рис. 3 иллюстрирует репрезентацию ветвления бронхиального дерева одним эквивалентным четырехполюсником. Операция повторяется необходимое число раз. Отметим, что в силу предполагаемой симметрии бронхиального дерева эквивалентные четырехполюсники между альвеолами, источниками напряжения и ветвлением заданного уровня во всем легком одинаковы.

Таким образом, анализ дыхательных шумов в любой точке ветвления сводится к анализу токов и напряжений в цепи, содержащей несколько эквивалентных четырехполюсников. Например, при анализе шумов в точке над трахеей один эквивалентный четырехполюсник будет соответствовать всему легкому ниже трахеи, второй – трахее и голосовому тракту; третий – моделировать звуковую проводимость тканей до поверхности кожи. При моделировании дыхательных шумов в ротовой полости весь респираторный тракт сводится к одному четырехполюснику.

Рассматриваемый подход позволяет: относительно легко учитывать большое количество элементов респираторного тракта (при 35 уровнях ветвления число учитываемых элементов больше 68 миллиардов); моделировать влияние возрастных изменений на дыхательные шумы; моделировать изменения этих шумов, вызванные различными легочными заболеваниями. Легочное заболевание моделируется изменением параметров электрической цепи (цепей) в определенной области легкого. В следующем разделе мы приведем результаты моделирования при астме.

Результаты

В качестве иллюстрации мы смоделировали частотные зависимости отношений давления на выходе (давление выдыхаемого воздуха в ротовой полости) к давлению на входе (альвеолярное давление) двух взрослых: здорового и больного с бронхообструктивным синдромом при бронхиальной астме на выдохе (рис. 4). В обоих случаях мы рассматривали простую симметричную модель ветвления воздушных путей с числом ветвлений 35. У больного предполагалось, что радиусы воздушных путей (внутренние радиусы трубок) r i уменьшились в два раза, а толщины стенок увеличились на r i /4 для ветвлений, начиная с номера 5 до 25, i = 5, …, 25. Все остальные параметры трубок не изменялись. Такое изменение параметров трубок может рассматриваться как приближенное моделирование астматического поражения воздушных путей. При моделировании учитывалось, что бронхиальная астма характеризуется обструкцией дыхательных путей и воспалительным процессом, который затрагивает все дыхательные пути от центральных к периферическим отделам трахеобронхиального дерева (мелким бронхам) [30]. Вариация области поражения, нижнего и верхнего значений i , не приводит к качественному изменению результатов.

В области частот от 200 до 1300 Гц наблюдается увеличение давления на выходе в обоих случаях. Однако в случае больного (см. рис. 4, а , красная кривая) это увеличение может быть более чем в два раза больше. В обоих случаях увеличение давления немонотонно с частотой. Вначале давление растет с частотой до первого максимума, примерно при 700 Гц, а затем резко снижается до минимума. У больного минимум и второй максимум наблюдаются при более низких частотах, чем у здорового. Отметим, что у здорового минимум опускается ниже давления на входе (давление в альвеолах), в то время как у больного давление на выходе в 1,8 раза больше давления на входе.

Дыхание сопровождается периодическим изменением давления в альвеолах, напряжения на входе. Это периодическое изменение можно представить в виде ряда Фурье (спектра Фурье), набора гармоник, частоты которых кратны частоте дыхания. Набор гармоник и частот специфичен для каждого человека. Однако, как показывают результаты моделирования, для сравнения дыхательных шумов здорового и больного достаточно сопоставить их амплитуды гармоник (огибающие) в достаточно широком диапазоне частот от 400 до 1300 Гц (см. рис. 4). Увеличение давления на выходе у больного должно соответствовать усилению амплитуд Фурье-спектра записанных дыхательных шумов в этой области частот. Этот результат хорошо согласуется с анализом реально записанных дыхательных шумов (рис. 5) и результатами, приведенными в [6, 7, 13].

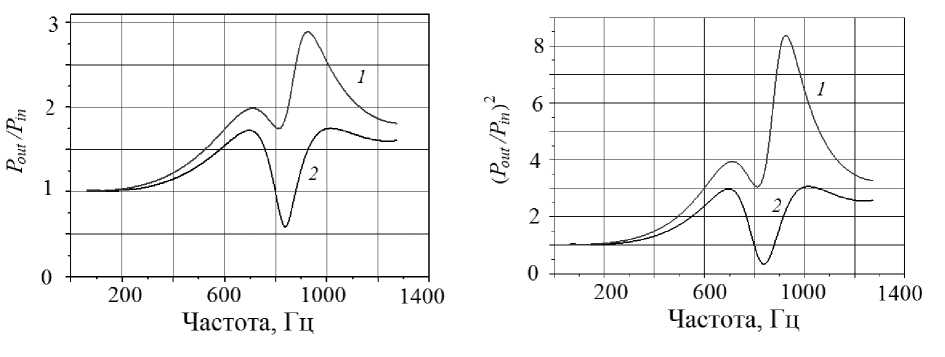
Рис. 4. Моделирование частотной зависимости отношения давления ( а ) и отношения частотной энергетической характеристики ( б ) на выходе к давлению на входе взрослых здорового ( 2 ) и больного ( 1 )

На рис. 5 приведены типичные Фурье-спектры дыхательных шумов, записанных с использованием разработанной нами системы их регистрации [7] в соответствии со стандартами «Компьютеризированный анализ дыхательных шумов» [16]. Она состоит из микрофона Sony ECM- 77 B , предусилителя, полосно-пропускающего фильтра, аналого-цифрового преобразователя и компьютера. Предусилитель, полосно-пропускающий фильтр и аналого-цифровой преобразователь конструктивно объединены во внешнюю звуковую плату Sound Blaster ( Singapore ), позволяющую переводить аналоговый сигнал в цифровой с частотой дискретизации 96 кГц. Для исключения низко- и высокочастотных шумов, не отражающих активность легких, частотный диапазон полосно-пропускающего фильтра был в пределах от 100 Гц до 2,5 кГц. Записи шумов производились в течение нескольких респираторных циклов, 25–30 с. Записи контролировались на наличие посторонних шумов и случайных вариаций интенсивности звука. Для сравнения амплитуд гармоник шумов, у больных и здоровых волонтеров, записанные шумы нормировались на их максимальные значения. Это позволило избежать влияния интенсивности дыхания на результаты. Частотноамплитудные характеристики шумов (см. рис. 5) определялись с использованием быстрого Фурье-преобразования. Более подробное описание процедуры измерений и обработки сигнала приведено в [6, 7].

Анализ изменений частотно-амплитудных характеристик Фурье-спектров, вызванных астматическим заболеванием, позволил нам разработать метод компьютерной (автоматической) диагностики заболевания [6, 7, 13]. Рассмотрение энергетических спектральных характеристик, пропорциональных квадрату давления, увеличивает разницу в спектрах больных с бронхообструктивным синдромом и здоровых (см. рис. 4, б ) и позволяет достичь более точной компьютерной диагностики [6].

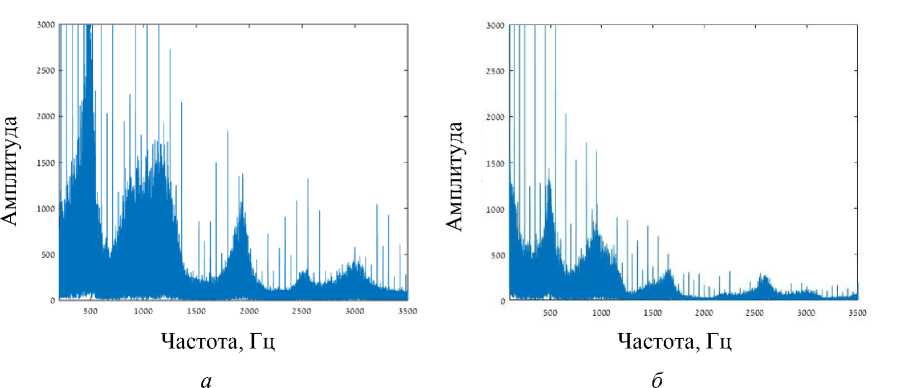
Рис. 5. Фурье-спектры, полученные при анализе шумов 14-летних девочек: а – страдающей астмой, во время обострения; б – здоровой. Запись в ротовой полости. Методика измерений описана в [7]. В обоих случаях записанный сигнал был нормирован на его максимальную величину. Теоретические результаты (см. рис. 4) хорошо совпадают с экспериментальными при частотах меньше 1500 Гц

Обсуждение

Созданная математическая модель распространения дыхательных шумов в респираторных путях имеет отношение к разработке передовых аускультативных методов, которые используют несколько неинвазивных датчиков для анализа дыхательных шумов человека [ 7, 8 ] . Любое функциональное моделирование органов сильно зависит от точности и репрезентативности имеющейся структурной модели. Ранее было отмечено, что это из-за отсутствия комплексных морфологических данных легкого человека предпочтительной моделью является модель трубок [20, 27]. С появлением реалистичного структурного описания легких и более точного отображения архитектуры легких моделирование, касающееся потока газа и осаждения частиц, теперь может быть выполнено с более высокой точностью.

Считается, что источником образования дыхательных шумов является вибрация стенок бронхов различного калибра, при этом сами стенки бронхиального дерева могут быть изменены вследствие отека, спазма и других патологических изменений [ 2 ] . Другой механизм образования этих шумов связан с потоком воздуха в легких и его изменениями во времени. В рассматриваемой модели оба механизма моделируются индуктивностями и емкостями в эквивалентной электрической цепи (см. рис. 2). Эти элементы цепи образуют резонансные контуры, которые приводят к усилению напряжения на выходе на определенных частотах; без индуктивностей и емкостей напряжение на выходе было бы меньше, чем напряжение на входе при всех частотах.

Дыхательные шумы, сопровождающие бронхообструктивный синдром, могут быть охарактеризованы как набор периодических волн с основной частотой в пределах от 100 до 2500 Гц. В работах [28, 29] указывается, что основная частота лежит между 100 и 1000 Гц и между 400 и 1600 Гц соответственно. Наши измерения в трех точках, ротовой полости, над трахеей, над правым легким, и их Фурье-анализ показал, что максимум шумов, вызванных этим заболеванием, лежит в этом диапазоне частот [6, 7, 13]. Как пример на рис. 5 приведены типичные Фурье-спектры, полученные при анализе шумов 14-летней девочки, страдающей астмой, во время обострения и здоровой 14-летней девочки. Предложенная математическая модель достаточно хорошо описывает амплитудно-частотную зависимость при частотах меньше 2 кГц, в области частот, где предположение о симметричном ветвлении справедливо [12]. При частотах меньше 1300 Гц модель предсказывает два максимума амплитудно-частотной зависимости, что подтверждается экспериментальными результатами. Численное различие между экспериментом и моделью можно объяснить следующими основными причинами: 1) расчеты проводились с использованием параметров, характеризующих легкое взрослого мужчины; 2) область поражения (нижнее и верхнее значения i), как и изменение толщины стенок воздушных путей, выбрана произвольно; 3) не учитываются шумы другого происхождения (сердечные, мышечные и т.д.), которые особенно важны при низких частотах; 4) модель не учитывает изменения упругости стенок дыхательных путей. Таким образом, предложенная аналоговая модель дает достаточно хорошее описание образования специфичных дыхательных шумов, свистящего дыхания, вызванных бронхообструктивным синдромом. Показано, что относительное усиление амплитуд гармоник (шумов) в характерном для специфического астматического дыхания диапазоне частот вызвано в основном сужением дыхательных путей.

Однако эта модель базируется на предположении малого изменения диаметра воздушных путей, когда характер воздушного течения не меняется. Такой подход не может смоделировать появление и длительность характерного для астмы свистящего дыхания продолжительностью от 80 до 250 мс [25]. На выдохе свистящее дыхание регистрируется несколько раз. Продолжительность каждого свистящего дыхания содержит от нескольких десятков до нескольких сотен периодов «усиленных» шумов. Этого достаточно для их четкой регистрации. Появление и длительность свистящего дыхания, можно предположить, определяются относительно медленными квазипериодическими (с периодом несколько герц) воздействиями на дыхательный тракт.

Комплекс признаков бронхиальной астмы может являться результатом проявления многих взаимосвязанных факторов, характеризующих бронхообструктивный синдром: легочной механикой, воспалением и ремоделированием стенок бронхов, активностью гладкой мускулатуры воздухоносных путей [15, 32]. Результаты исследований показывают, что комплексная модель сужения бронхов, описывающая результат взаимодействия гладкой мускулатуры воздухоносных путей, воздушного потока, давление в грудной клетке, может объяснить комплекс свойств, проявляющихся из-за сужения бронхов, вызванных самоорганизацией неоднородностей в строении воздухоносных путей и больших смежных областей с плохой вентиляцией (вентиляционные дефекты) [31, 32]. Математические модели, разработанные для описания процессов в легких при астме [1, 3, 4, 9–11, 14, 18, 19, 21–24, 26, 32, 33], насколько нам известно, не описывают усиление дыхательных шумов. Совместное использование математических моделей, описывающих изменение альвеолярного давления, динамику стенок воздушных путей, распространение шума по грудной клетке, и предложенной модели образования дыхательных шумов позволит более точно моделировать астматическое свистящее дыхание и понять процессы в легких и их взаимное влияние.

Заключение

Для преодоления ряда трудностей при анализе дыхательных шумов авторы использовали аналоговое моделирование, при котором рассмотрение воздушных потоков в воздухоносных путях легкого заменяется рассмотрением электрических процессов. Предложенное аналоговое моделирование показало, что усиление дыхательных шумов в характерном для бронхиальной астмы частотном диапазоне связано с сужением дыхательных путей. Это усиление, используя электротехническую аналогию, носит резонансный характер. Рассматриваемый подход позволяет относительно легко учитывать большое количество элементов респираторного тракта и моделировать изменения этих шумов, вызванные различными легочными заболеваниями. Предложенная математическая модель может помочь в разработке более точной компьютерной диагностики при анализе дыхательных шумов, а ее совместное применение с другими моделями позволит лучше понять процессы в легком.