Математическая модель разгонного ламинарного течения ньютоновской жидкости в анизотропном пористом канале прямоугольного сечения

Идентификация явлений переноса в технических и технологических системах широкого предметного назначения достигается применением пористых материалов природного и искусственного происхождения, которые обеспечивают максимально возможную удельную площадь поверхности межфазного взаимодействия [1,2]. Режим функционирования таких систем, как правило, нестационарный, так как входные характеристики потоков (расход, давление, температура и др.) существенным образом зависят от времени (например, в случае электрохимических устройств [3] сжигания углеводородно-нейтральных и возобновляемых видов топлива [4], а также микрохимических реакторов [5]).

Наряду с очевидными преимуществами пористых сред, существует и ключевой недостаток - значительное гидравлическое сопротивление [6], т.е. их использование эффективно тогда, когда увеличение количественных показателей реперных потенциалов будет превышать энергетические затраты на прокачку рабочего тела [7]. Проведение такого анализа путем прямого интегрирования системы фундаментальных уравнений непрерывности и переноса импульса Навье – Стокса невозможно из-за практически неформализуемой топологии порового пространства [8], что привело к синтезу макроскопических [9, 10] и микроскопических [11, 12] моделей. Модели макроскопического типа основываются на уравнении Дарси – Бринкмана – Форчхеймера [13], однако адекватность их применения для оценки нестационарных режимов еще предстоит верифицировать [14]. Тем не менее, при допущении об однонаправленности течения [15] в [16] было получено аналитическое решение задачи о начальном гидродинамическом участке изотропного пористого канала с прямоугольным поперченным сечением. Микроскопические модели базируются на детальной архитектуре парового пространства, имеющей регулярную структуру [17], причем не ясна правомерность использования такого подхода для описания порового пространства со стохастической структурой. Кроме того, эксперименты в микрометровом масштабе показали [18], что из-за неоднородности течения может происходить скольжение на границе жидкость – твердое тело, причем величина проскальзывания носит динамический характер и это обстоятельство затрудняет ее определение.

Наметившийся тренд дальнейшей интенсификации явлений переноса за счет пористых сред с заданной анизотропной структурой [19, 20] вызвал необходимость оценки гидродинамических параметров для них в нестационарных режимах и, в частности, определения времени выхода на стационарный режим в циркуляционном контуре охлаждения [21] с учетом времени релаксации напора.

1.    Постановка задачи

Рассматривается развитие напорного ламинарного течения вязкой несжимаемой жидкости в полубесконечном горизонтальном анизотропном пористом канале прямоугольного поперечного сечения высотой h _z и шириной h _x (рис. 1) при нарастающем градиенте давления до постоянного значения за конечное время τ 0 .

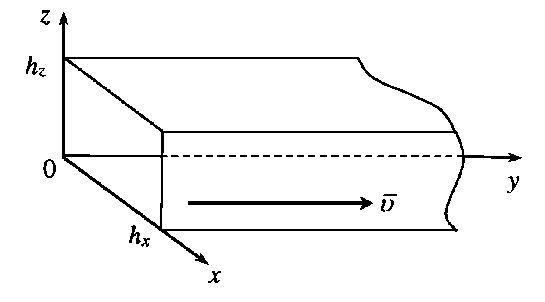
Рис. 1 . Расчетная схема

Макроскопическая модель гидродинамики в пористой среде представляется уравнением Дарси – Бринкмана – Форчхеймера без учета инерционного эффекта (допущение обосновано для ламинарного режима течения в [22]) в форме Ксу – Ченга [23]:

V • и = 0;                                    (1)

+ ⁽£ .v ) и =    ( -v p + £ f v 2 u - $ и ) ,               (2)

∂τ ε         ρf         ε K где т - время, с; ■£ - вектор скорости сатурированной жидкости во внутрипоровом пространстве, м/с ; ρf , µf – плотность и динамическая вязкость жидкой фазы, кг/м 3 , Па·с; ε – пористость; p – абсолютное давление, Па; K – проницаемость, м2 . Для изотропной пористой среды проницаемость является скалярной величиной, а в случае анизотропии – ортотропным тензором [24] по причине более простого экспериментального определения его компонентов.

Введем обозначение тензора проницаемости как K . Известно [25], что Якобианы вращения декартовой системы координат вокруг осей ox , oy , oz на углы α , β , γ таковы:

J (α) =

cos α

- sin α

; J (β) =

cos β 0

sin β 0

;

sin α

cos α

cos γ

- sin γ

- sin β

0 "

cos β

J (γ) =

sin γ 0

cos γ 0

,

поэтому матрица вращения есть

A=J(α)J(β)J(γ)= cos β cos γ                   - cos β sin γ             sin β sin α sin β cos γ + cos α sin γ sin α sin β sin γ + cos α cos γ - sin α cos β - cos α sin β cos γ + sin α sin γ cos α sin β sin γ + sin α cos γ cos α cos β

Структура ортотропного тензора проницаемости имеет диагональный вид в выбран- ной системе координат

K 0 =

K x 0   0

0 K y 0

0   0  Kz или в инвариантной форме записи

K¯ = AK¯0AT, где его компоненты равны

K xx = cos ² β cos ² γK x + cos ² β sin ² γK y + sin ² βK z ;

K xy = K yx = cosβ cosγ (sin α sin β cosγ + cos α sinγ) K x -- cosβ sinγ ( - sin α sinβ sinγ + cosα cos γ) K _y - sin α sinβ cosβK _z ;

K xz = K zx = cosβ cosγ ( - cosα sinβ cosγ + sin α sinγ) K x -

• - cos β sin γ (cos α sin β sin γ + sin α cos γ) K _y + cos α sin β cos βK _z ;

K _yy = (sin α sin β cosγ + cos α sinγ) ² K _x + ( - sin α sinβ sinγ + + cos α cos γ) ² K y + sin ² α cos ² βK z ;

K _yz = K _zy = (sin α sinβ cosγ + cos α sinγ) (cos α sinβ sinγ + sin α sin γ) K _x +

+ (sin α sinβ sinγ + cos α cos γ) (cos α sinβ sinγ + sin α cos γ) K y - sin α cos α cos ² βK z ;

K _zz = ( - cosα sin β cosγ + sin α sinγ) ² K _x + (cos α sinβ sinγ +

+ sinα cosγ) ² K y + cos ² α cos ² βK z .

Составляющая Дарси для анизотропного случая преобразована следующим образом

^fи/K = ^f K-1 U/ (k • K-1) = ^f K-1U/E, где K-1 – обратный тензор проницаемости; E – единичный тензор. Умножение на E слева трансформирует (2) с учетом (3) к виду d^+ (- »v) U =   (—Vp + 'V2U + ^f K-1u) .

∂τ ε           ρfε

Компонентная форма записи системы (1), (4), в предположении однонаправленности течения по оси oy, т.е. U= (0,uy, 0), такова duy = —dp + L (d2Uy + d2Uy — "If K* U

∂τ      ρf ∂y   ρf   ∂x2    ∂z2      ρf yy y , где

K yy = [F y (a, в, Y) K y + F x (a, в, Y) K x + F z (a, в)] /K, F _y (a, в, Y) = — cos ² a cos ² в cos ² y + 2 cos ² a cos y + cos ² в cos ² y + + cos ² a cos ² в — cos ² y — cos ² a — cos ² в + 1 — 2 sin a cos a sin в sin y cos y ; F _x (a, в , Y ) = — cos ² в cos ² Y + cos ² a + cos ² Y — 2 cos ² a cos ² Y + + cos ² a cos ² в cos ² y + 2 sin a cos a sin в sin y cos y ;

F z (a, в) = cos ² в — cos ² a cos ² в; K _y* = K z /K y ; K x = K z /K x .

Уравнение (5) дополняется краевыми условиями:

Uy (x, z, 0) = 0;

Uy (0, z, т) = Uy (hx, z, т) = Uy (x, 0, т) = Uy (x, hz, т) = 0, а градиент давления представлен псевдомультипликативным комплексом dpjyRr) = dp (y)

∂y dy + где dp (y) /dy = const,

1 + (т) = {

т /т о , 0 < т < т о , 1,     т ₀ < т <  то

– модифицированная односторонняя функция Хэвисайда [26]. Система (5) – (7) в безразмерной форме записи такова:

dv = C1+ (т) + Re-1 (d2V + д2Л —, (Re. Da)-1 w;

∂θ∂X ∂Z

V (X,Z, 0) = 0;

V (0, Z, 0) = V (Hx, Z, 0) = V (X, 0,0) = V (X, Hz, 0) = 0, где 0 = ит/dh; 0o = uто/dh; X = x/dh; Z = z/dh; V = Uy/u; dh = 2hxhz/ (hx + hz) -гидравлический диаметр канала, м; ■- - среднеинтегральная скорость жидкости по перечному сечению канала при 0 ^ то; Re = pfdhU/^f - число Рейнольдса; Da = Kz/dh - число Дарси; P = p/ (pfU2); Ф = Fy (a,в,Y) Ky + Fx (a,в,Y) Kx + Fz (a, в); C = — edP/dY; Y = y/dh.

2.    Решение

Результат применения одностороннего интегрального преобразования Лапласа [27] по переменной θ к начально-краевой задаче (8) – (10):

L + L — (Re   ' Da 1Ф^Ъ) =g Г [1 - exp (—60s)] ;

∂X2    ∂Z2

Vl (0, Z, s) = Vl (Hx, Z, s) = VL (X, 0, s) = Vl (X, Hz, s) = 0, где Vl (X,Z,s) - изображение V (X, Z, 6). Конечные интегральные синус-преобразования Фурье [28] по переменной X

H

x

F x [ V l (X, Z, s

)

V l (X, Z, s) sin (A m X) dX = V lF x (A m , Z, s),

где A m = mn/H x , m = 1, то , и по переменной Z

H

z

F Z ^[ V LF x ^{( A} m , ^{Z,s )]} = I

V LF' x (A m , Z, s) sin (^ n Z ) dZ = V bF _xF_z (A m , Ц п , s),

где ц _п = nn / H z , n = 1, то , вначале переводят систему (11), (12) в краевую задачу для обыкновенного дифференциального уравнения

”ТуТ^" - ( ^A m ⁺ s ^Re + ^{Da 1 ф} ) VLF' x = -А— п 2 ^[1 - ^{cos ( A} m H x ^{)] [1 — exp ( — 6} 0s ^)] ;

dZ ^{2 m                        x}      λ _m θ ₀ s ²

VLFx (Am, 0, s) = VLFx (Am, Hz, s) = 0, а потом в алгебраическое соотношение

V LF x F z = CRe ^{[1 — cos ( A} m H x ^{)] [1 — cos (} ^ n ^H z ^{)] [1 — exp ( — 6} 0 ^{s )]} / / [ A m ^ n B o s ² ( A m + ц П + s Re +s Da ¹ Ф )] .

С помощью формул обращения [27, 28] примененных интегральных преобразований получено из (13) решение:

∞∞

^{V ( X} , ^Z , ^{6 )} = TT it ^^     A2— ^{{ — 1 +} b mn ^{6 1}+ ^{( 6} 0 ^{— 6 ) + exp ( —}b mn ^{6 ) +}

^{H x H z} m =1 n =1 ^{b 2} mn

+ B o b mnj | sin (A m X) sin (^ n Z) ,

b mn    θ 0 b mn       b mn    θ 0 b mn

+ 1+ (6 — 6o) 2exp I — 6 + ^— I sh I — 6— I где amn   [1 cos (AmHx)] [1   cos (^nHz)] / (Amцп60), bmn   (Am + Mn + ^Da Ф) /Re.

Константа С определена из условия

H x H z

H x H z

У У V (X, Z, то) dXdZ = 1, откуда

∞∞

C = ^lim_u ., ^^ ^^ 73— {- 1 + b mn ^1 + ^{( 9} 0 - ^{9 )} + ^{exp ( - b} mn ^{9 )} + Hx Hz^ fe bm»

+ 1 + ^{( 9} - ⁹ 0 )

.2exp (-9+

⁹ 0 b mn

а коэффициент гидравлического сопротивления ξ из закона Дарси [1]:

dP = £

P f u ² dy

2 dh¹

т.е.

( = - 2C ( e.

Время установления стабилизированного течения θ ^∗ найдено при допустимом отклонении в 1% из уравнения

| 1 - V (1/2,1/2, 0 * ) /V (1/2,1/2, _TO ) | = 0, 01.

3.    Анализ

Проверка адекватности синтезированной математической модели проводилась на основе сравнительного анализа с аналитическим решением при напорном стационарном ламинарном течении вязкой несжимаемой жидкости в горизонтальном анизотропном пористом полубесконечном канале [29] формата 2-D. В этом случае ось ox (рис. 1) нивелируется, причем К / = 0 , в = Y = 0 и 9 о = 0, 01 , а для того, чтобы канал с прямоугольным сечением соответствовал плоскому каналу с сечением в виде полосы, достаточно выполнение условия H x ^ H z (например, H x : H z = 10 : 1 ). Если положить а = 0 и варьировать коэффициентом проницаемости К у , то как показано на рис. 2 выраженная гидравлическая анизотропия в направлении оси Oz приводит к более однородному профилю скорости, а изменение ориентации проницаемости от базовой системы координат zOy на угол α вызывает аналогичную трансформацию профиля скорости (рис. 3).

Результаты сравнения позволили применить предложенную математическую модель для оценки зависимости времени установления разгонного течения от времени достижения постоянства градиента давления в условиях анизотропности пористой среды. Увеличение трансверсальной проницаемости по отношению к аксиальной выравнивает поле скоростей по поперечному сечению канала с возрастанием соответственно коэффициента гидравлического сопротивления (рис. 4). Влияние угла ориентации выражено в меньшей степени (рис. 5). Продемонстрирована практически линейная функциональная связь между временем установления течения и временем достижения постоянного перепада давления.

Заключение

Разработана адекватная математическая модель для определения гидродинамических характеристик разгонного течения вязкой несжимаемой жидкости в пористом

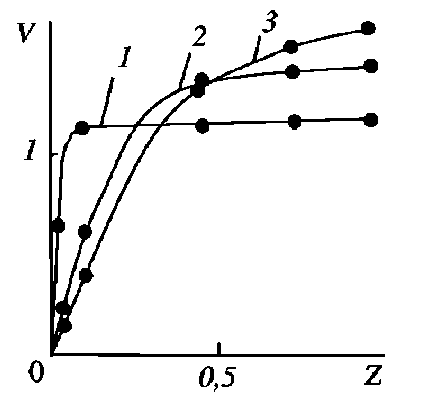
Рис. 2 . Профили скоростей установившегося течения в плоском канале при H x = 10 , H z = 1 , Da = 4 • 10 - 3 , a = 0 , Re = 10 , ε = 0 , 4 , θ ₀ = 0 , 01 для различных коэффициентов гидравлической проницаемости K * : 1 - 10; 2 -1; 3 – 0,1; • – данные [29]

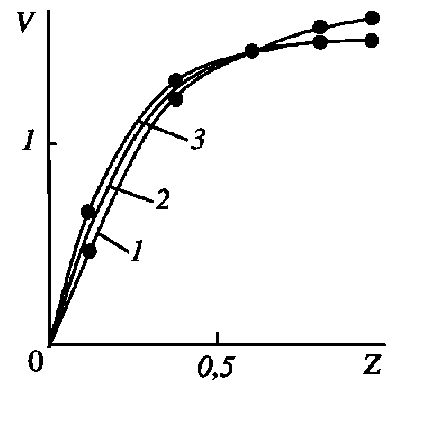
Рис. 3 . Профили скоростей установившегося течения в плоском канале при H x = 10 , H z = 1 , Da = 10 ^{- 2} , K * = 0 , 25 , Re = 10 , ε = 0 , 4 , θ ₀ = 0 , 01 для различных значений угла ориентации a : 1 - 0; 2 - 30 ° ; 3 - 90 ° ; • - данные [29]

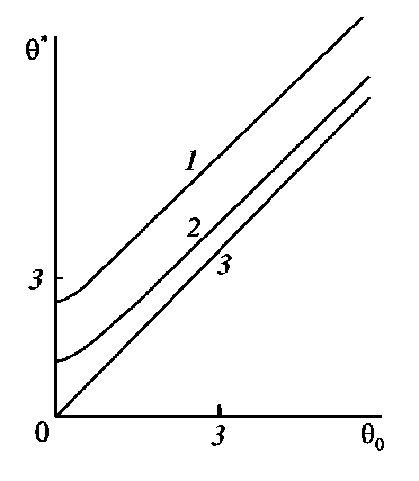
Рис. 4 . Время установления разгонного течения при H _x = H _z = 1 ; Da = 10 - 2 ; a = 0 ; Re =10 ; e = 0,4 для различных значений угла ориентации K * : 1 – 0,1; 2– 1; 3–10

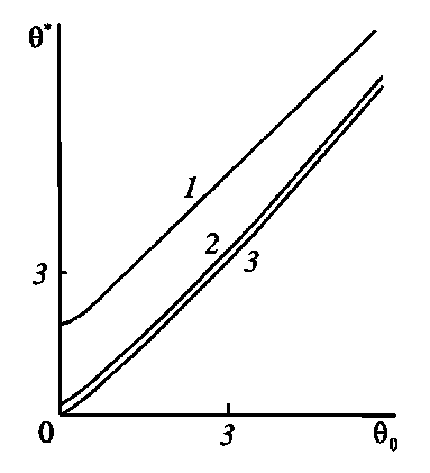
Рис. 5 . Время установления разгонного течения при H _x = H _z = 1 ; Da = 10 - 2 ; K * = 0,1 ; Re =10 ; e = 0,4 для различных значений угла ориентации a : 1 - 0; 2 - 30 ^° ; 3 - 90 ^°

анизотропном канале с прямоугольным сечением, которая позволяет идентифицировать время установления поля скоростей в зависимости от времени стабилизации градиента давления, коэффициента проницаемости и угла ориентации в анизотропной матрице.

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 19-38-90114.