Математическая модель регуляции углеводного обмена с учетом функциональных нарушений для прогнозирования риска ассоциированных заболеваний

докринной системы [3]. К нарушениям углеводного обмена относятся заболевания с повышенным содержанием глюкозы в крови1. По данным ВОЗ (всемирная организация здравоохранения) (2022), диабетом страдает более 800 млн человек, что составляет около 10 % всего населения планеты. Сахарный диабет – это группа метаболических (обменных) заболеваний, характеризующихся гипергликемией, которая является результатом дефектов секреции инсулина, действия инсулина или обоих этих факторов [4].

Сахарный диабет первого типа связан с нарушениями секреции инсулина в результате разрушения инсулинпродуцирующих ß-клеток и чаще выявляется у молодых пациентов до 30 лет с поражением более 80 % инсулинпродуцирующих клеток2. К механизмам развития диабета относят поражения поджелудочной железы аутоиммунного характера после вирусной инфекции или токсического воздействия. При сахарном диабете 2-го типа ткани невосприимчивы к действию инсулина, при этом его уровень в крови может быть нормальным или повышенным. У большинства (85 %) пациентов выявляется сахарный диабет 2-го типа. Снижению восприимчивости ткани к инсулину способствует ожирение, так как жировая ткань дополнительно блокирует пути воздействия инсулина [5].

В системе регуляции уровня глюкозы основными являются два гормона поджелудочной железы: инсулин и глюкагон. Инсулин и глюкагон действуют вместе, чтобы сбалансировать обмен веществ. Увеличение концентрации глюкозы в крови стимулирует высвобождение инсулина. Поджелудочная железа выделяет глюкагон, когда уровень глюкозы в крови падает слишком низко. Глюкагон повышает уровень глюкозы в крови за счет усиления транспорта гликогена из печени, а инсулин усиливает использование глюкозы тканями [6].

Для описания взаимодействия инсулина и глюкозы разрабатываются математические модели, с помощью которых можно получать оперативные прогнозные характеристики процессов в различных сценарных условиях. Модель, предложенная R. Hovorka et al. [7], описывает кинетику глюкозы при внутривенном введении, учитывая ее распределение между плазмой и тканями, инсулинзависимое и независимое потребление, а также подавление выработки глюкозы печенью под действием инсулина. В целом модель состоит из 9 обыкновенных дифференциальных уравнений и 15 параметров. Параметры модели были получены либо из клинических исследований на людях с диабетом 1-го типа, либо из распределений вероятностей в попу- ляции. В модели, предложенной J.T. Sorensen3, также используется камерный подход. Эта модель была первоначально разработана для описания процессов в здоровом организме с использованием 22 нелинейных дифференциальных уравнений, включая 3 уравнения для описания эндогенной секреции инсулина. Значения параметров были получены из литературы для среднестатистического индивида.

В модели, представленной в статье P.G. Fabietti et al. [8], учитывается поступление глюкозы в кровь из желудочно-кишечного тракта (ЖКТ), при этом рассматриваются быстро и медленно всасывающиеся углеводы. Особенностью модели является синусоидальное представление циркадной вариабельности чувствительности к инсулину. Четыре из 14 параметров модели были оценены на основании клинических данных. Модель является модификацией так называемой «минимальной модели» [9], являющейся одной из наиболее простых для более или менее адекватного описания процесса взаимодействия инсулина и глюкозы при внутривенном введение глюкозы.

Модель, представленная в статье M. Lombarte et al. [10], предназначена для описания гомеостаза глюкозы и инсулина у здоровых крыс системой уравнений, учитывающих поступление глюкозы из ЖКТ, утилизацию глюкозы тканями, производство глюкозы печенью, секрецию инсулина, клиренс инсулина, баланс базальных уровней глюкозы и инсулина. Модель имеет ряд ограничений, включая применимость лишь к здоровым крысам, упрощенное представление регуляции глюкозы без учета влияния других гормонов и индивидуальных вариаций, отсутствие временных задержек и неспособность моделировать инсулинорезистентность, являющуюся ключевым механизмом при диабете второго типа. Модель полезна для изучения базовых механизмов гомеостаза глюкозы, но ее прогностическая ценность ограничена из-за игнорирования сложных регуляторных взаимодействий и патологических состояний. Кроме того, сложность представляет вопрос переноса результатов моделирования на организм человека.

Модель, представленная в статье C. Dalla Man et al. [11], подробно описывает систему регуляции глюкозы, но имеет большое количество математических уравнений (12 дифференциальных и 18 алгебраических) и требует сложных методик для оценки множества параметров. Следует отметить, что самая быстрая петля обратной связи заключается в высвобождении накопленного инсулина сразу после стимулирования глюкозой за счет повы- шенных концентраций глюкозы в крови4. Этот первый пик инсулина достигает максимума примерно через 3–5 мин после введения глюкозы. Вторая петля обратной связи обусловлена глюкозозависимым усилением обеспечения инсулином, что дает видимый эффект примерно через 10 мин5. В связи с этим при разработке математических моделей важно учитывать времена запаздывания.

В модели, описанной в статье M. Gallenberger et al. [12], учитывается постоянный прирост скорости поступления глюкозы в крови за счет разницы между поступлением из печени и потреблением мозгом и нервными тканями. Скорость убывания глюкозы в крови описывается слагаемыми, учитывающими как инсулиннезависимое, так и инсулинзависимое потребление другими органами. Динамика концентрации инсулина в крови описывается через разность скоростей секреции и выведения из организма. Некоторые модели регуляторной системы «глюкоза – инсулин», представленные, например, в статьях [13, 14], описывают не только динамику массы глюкозы, инсулина, но и учитывают изменение количества β-клеток.

Модель, предложенная Н.А. Широковой [15, 16], описывает баланс инсулина и глюкозы при сахарном диабете через систему двух дифференциальных уравнений, учитывая поступление глюкозы с пищей, критические уровни для описания процесса выведения глюкозы через почки при гипергликемии, инсулинзависимое потребление глюкозы, выработку глюкозы печенью. Следует отметить, что модель, предложенная Н.А. Широковой, так же как и некоторые другие модели, не учитывает инсулиннезави-симое потребление глюкозы.

Резюмируя результаты обзора, целесообразно разделить модели на базовые, учитывающие только основные элементы системы, и комплексные, в которых рассматриваются промежуточные стадии преобразования элементов и дополнительные процессы.

В табл. 1, 2 приведены результаты сравнения базовых существующих моделей, описывающих гормональную регуляцию уровня глюкозы в крови, а также вид основных слагаемых математической модели, предложенной авторами данной статьи. Более комплексные модели6 [7, 10, 11] имеют общие недостатки, в первую очередь – большое количество параметров и необходимость проведения множества дополнительных метаболических исследований для их оценки. Это вынуждает использовать в численных расчетах средние значения, снижая достоверность результатов и ограничивая применимость моделей на индивидуальном уровне.

Анализируя данные табл. 1 и 2, можно заметить, что поступление глюкозы в кровь полагается константой или описывается некоторой функцией от времени, отражающей потребление пищи и всасывание глюкозы из ЖКТ в кровь. Вывод глюкозы в кровь, инсулиннезависимое потребление, а также

Таблица 1

Сравнение базовых математических моделей (слагаемые в уравнении для глюкозы)

Источник	Потребление глюкозы	Поступление глюкозы	Вывод глюкозы	Печеночная выработка глюкозы
Millsaps K. et al. 7 [21]	кр кр K 6 C гл C инс	–	–	–
De Gaetano A. et al. [14]	- K 1 с кр - K 6 c кр c-	K = const	–	–
Широкова Н.А. [15]	- K 6 ск Cz	f ( t )	- K 1 (( с кр - с кр**))	K 4 <  ( C кр* - с кр ) >
Hussain J. et al. [17]	- K 1 C KP - K 6 с гл с X	K = const	–	–
Lombarte M. et al. [10]	- K 10 - K 6 с X	f ( t )	–	к 4 <  ( C кр* - с кр ) >
Gallenberger M. et al. [12]	- k 1 C кр - k 6 с кр с кн	f ( t )	–	–
Предлагаемые в данной статье	- K  - k 6 с гр ( t ) с кн t ) 10      к 7 + с кр ( t )	f ( t )	- к 1 F n C кр ( t )	-{ ( C кр ( t - t 1 ) - C кр* )} K 4 F ne4 + C ( t - t 2 ) ■ ■( ( C Г - C кр ( t - 1 3 ) )) K 5 F ne4

Примечание: * – обозначения приведены в разделе «Концептуальная и математическая постановки задачи».

Таблица 2

Сравнение базовых математических моделей (слагаемые в уравнении для инсулина)

Источник	Выработка инсулина	Выведение инсулина
Millsaps K. et al.7	кр K 2 C гл	кр 2 K 3 C инс
De Gaetano A. et al. [14], Hussain J. et al. [17], Lombarte M. et al. [10], Gallenberger M. [12]	K 2 C г к л р	кр K 3 C инс
Широкова Н.А. [15]	K 2 {( C кр - C кт )}	кр кр K 3 C инс C гл
Предлагаемые в данной статье	K 2 f di1 c : ( t - 1 4 ) C Л t - 1 5 )	- K 3 F n C X ( t )

Примечание: * – обозначения приведены в разделе «Концептуальная и математическая постановки задачи».

выработка глюкозы печенью представлены в меньшем количестве работ, что указывает на то, что эти процессы часто игнорируются. Динамика инсулина во многих базовых моделях описывается схожими слагаемыми. В предложенной авторами данной статьи новой базовой модели учтены все указанные процессы, а также дополнительное регуляторное воздействие глюкагона путем добавления соответствующих слагаемых и уравнения в математическую постановку. Кроме того, в модель введены функциональные нарушения органов (печени, почек, поджелудочной железы), временные задержки по передаче регуляторных сигналов, а также модель позволяет учесть различные режимы питания (фастфуд с высоким содержанием быстрых углеводов, высококалорийная пища, несбалансированное в течение суток питание).

Цель исследования – разработка математической модели регуляции углеводного обмена с учетом эндокринной функции поджелудочной железы и функциональных нарушений в организме при различных режимах питания.

В работе представлены: содержательная постановка задач с описанием рассматриваемого физиологического процесса; новая концептуальная постановка с созданием структурной схемы процесса; математическая постановка, включающая в себя запись уравнений баланса глюкозы, инсулина и глюкагона в крови и глюкозы в печени; подходы к идентификации параметров модели; численное решение и анализ результатов с их верификацией.

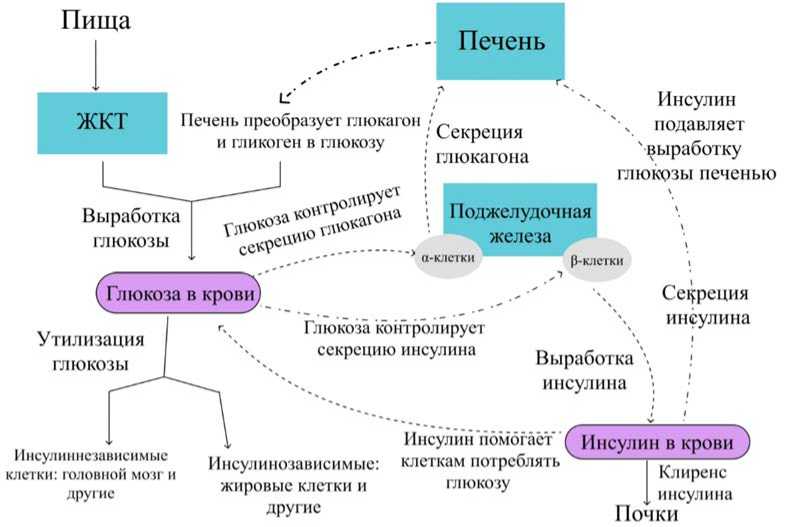
Концептуальная и математическая постановки задачи. На рис. 1 приведено схематичное представление регуляции углеводного обмена с учетом основных элементов системы.

При построении модели принимаются следующие концептуальные гипотезы:

• ■    в математической постановке будут использоваться обыкновенные дифференциальные уравнения (ОДУ) с запаздыванием;

• ■    интенсивность выработки инсулина поджелудочной железой пропорциональна концентрациям глюкагона и глюкозы в крови;

• ■    в организме непрерывно происходит потребление глюкозы тканями и органами, интенсивность этой утилизации описывается двумя составляющими, первая из них пропорциональна концентрациям инсулина и глюкозы с учетом насыщения (инсулинзависимое потребление), вторая – пропорциональна концентрации глюкозы (инсулиннезави-симое потребление);

• ■    при понижении уровня глюкозы ниже нормального под действием глюкагона происходит выход глюкозы из печени для поддержания нормального содержания ее в крови, при повышении уровня глюкозы в крови происходит обратный процесс;

• ■    вывод глюкозы, глюкагона и инсулина из организма осуществляется через почки, скорость их выведения пропорциональна соответствующим концентрациям;

• ■ скорость секреции глюкагона обратно пропорциональна концентрациям инсулина и глюкозы, что обеспечивает обратную связь в регуляторном контуре.

В данной работе для исследования процесса углеводного обмена используется следующий набор переменных: концентрация глюкозы в крови ( C _г^к_л^р ), концентрация инсулина в крови ( C _и^к_н^р_с ), концентрация глюкагона в крови ( C _г^к_н^р ), а также концентрация глюкозы в печени ( C _г^п_л^еч ), которая запасается в ней в виде гликогена.

Глюкоза в крови

Инсулиннезависимыс клетки: головной мозг и другие

И неуд и нозависи мыс: жировые клетки и другие

Инсулин помогает Г Инсулин в крови ют    гичгтюгл патк ^                   ■ ■^

клеткам потрсолять глюкозу

Клиренс инсулина Почки

Пища

• - Печень жкт

Р-клетки

Выработка глюкозы

Секреция инсулина

Выработка инсулина

Утилизация глюкозы

Секреция глюкагона

Глюкоза контролирует секрецию инсулина

Инсулин

■х подавляет 'выработку глюкозы печенью

Печень преобразует глюкагон и гликоген в глюкозу

Поджелудочная железа се«Р®“ ...........

Рис. 1. Схематичное изображение регуляции углеводного обмена

С учетом принятых обозначений и гипотез разработана концептуальная схема для описания процесса углеводного обмена, приведенная на рис. 2.

В математической постановке задачи для описания динамики введенных выше четырех переменных используется система ОДУ (обыкновенных дифференциальных уравнений) c запаздывающим аргументом в следующем виде:

C = f ( t ) - K 1 F n C - ( t ) - ( C KP ( t - t i ) - C KP* ) K ₄ F ne4 +

+ C KP ( t - 1 2 ) ( C KP** - C - ( t - 1 3 ) ) K 5 F ne4 -

- K6 CK (t) C■ t) - K(1)

K 7 + CKP (t)

dC^ = K2F»!CKP (t -14) CKHP (t - t‘ ) - K3FnCx (t),(2)

dC г ^кр

^K 8 ^F пж2

- K 9 F_nC KP ( t ),

dt     c KP ( t - 1 6 ) c x ( t - 1 7 )

печ dC^ =( ( CKP (t - ti )-CKP* )} K4 Fne4 -

- CKP (t - 12 )(( CKP** - CKP( t - 13) )) K5 Fne4,(4)

где K 1 – коэффициент, отражающий скорость выведения глюкозы почками, 1/с;

K ₂ – коэффициент, отражающий скорость секреции инсулина поджелудочной железой, л ∙ мкЕд /(с ∙ ммоль²);

K 3 – коэффициент, отражающий скорость выведения инсулина почками, 1/с;

K 4 и K 5 – коэффициенты, отражающие скорости потока глюкозы между кровью и печенью, 1/с, л/(с ∙ ммоль), если концентрация глюкозы в крови C _гл^р больше критического значения C _гл^р* , то поток глюкозы идет из крови в печень, если концентрация глюкозы в крови C _гл^р меньше критического значения C _гл ^р** , то поток идет из печени в кровь;

K 6 и K 7 – коэффициенты, отражающие скорость инсулинзависимого потребления глюкозы организмом (питания), ммоль/(с ∙ мкЕд), ммоль/л;

f (t) – функция поступления глюкозы в кровь из желудочно-кишечного тракта в зависимости от времени;

K 8 – коэффициент, отражающий скорость секреции глюкагона поджелудочной железой (ммоль² ∙ мкЕд) /(с ∙ л³);

K ₉ – коэффициент, отражающий скорость выведения глюкагона почками, 1/с;

K 10 – коэффициент, отражающий скорость ин-сулиннезависимого потребления глюкозы организмом, ммоль/(с ∙ л);

F п – функциональность почек;

F печ – функциональность печени;

F _пж1 – функциональность поджелудочной железы при выработке инсулина;

F _пж2 – функциональность поджелудочной железы при выработке глюкагона;

• t_i – коэффициент запаздывания, i принимает значения от 1 до 7;

• < > – скобки Мак-Кейли, возвращают значение 0, если аргумент отрицательный, и возвращают сам аргумент, если он положительный.

  

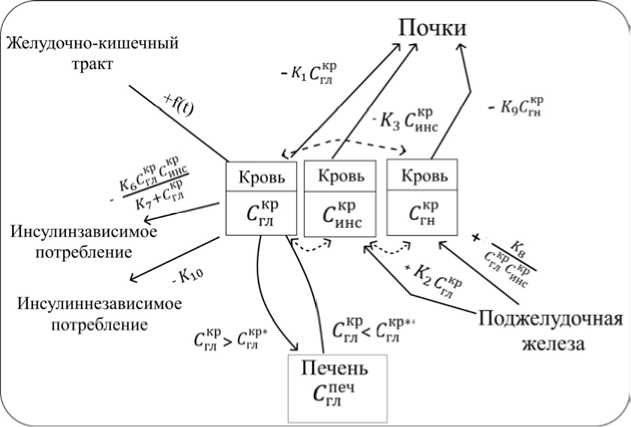
  Рис. 2. Концептуальная схема для описания процесса углеводного обмена

  
  

Левые части уравнений представляют собой производные переменных по времени (скорости изменения концентраций). В четвертом уравнении содержатся слагаемые скорости обмена глюкозы между кровью и печенью, аналогичные по модулю приведенным в первом уравнении, но с обратным знаком. Наличие функциональных нарушений органов будет приводить к корректировке скоростей изменения переменных в тех слагаемых, где функциональность выступает в качестве дополнительного мультипликатора, принимающего значения от 0 до 1. При снижении функциональности печени уменьшаются скорости запасания глюкозы и выхода из депо, при нарушении функциональности почек снижается скорость выведения веществ из организма, а при уменьшении функциональности поджелудочной железы снижается выработка гормонов (инсулина и/или глюкагона). Дополнительно можно учесть нарушения работы ЖКТ изменением функции поступления углеводов в кровь f ( t ). Кроме того, регулируя вид функции f ( t ), можно описать различные нарушения режима и рациона, учесть поступление в кровь быстрых и медленных углеводов, в том числе несбалансированное по времени.

Результаты и их обсуждение. В рамках исследования рассматриваются четыре сценария, которые описывают различные состояния организма и рационы питания. В первых трех сценариях рассматривается сбалансированное питание в течение суток с преимущественным потреблением медленных углеводов относительно быстрых. Четвертый сценарий описывает несбалансированное питание с преобладанием в рационе быстрых углеводов относительно медленных.

• 1.    Первый (базовый) сценарий описывает процесс без нарушений в организме, и функциональность всех органов принимается равной единице.

• 2.    Второй сценарий описывает ситуацию при диабете 1-го типа. При этом заболевании поджелудочная железа не может вырабатывать достаточное количество инсулина. В этом сценарии функциональность поджелудочной железы снижена и равна F _пж1 = 0,5, что соответствует значительному снижению выработки инсулина, при которой развивается сахарный диабет. Кроме того, F _печ = 0,5, что соответствует сопутствующему снижению функциональности печени по преобразованию глюкозы в гликоген и обратно.

• 3.    В третьем сценарии рассматривается диабет 2-го типа. В этом случае организм становится менее чувствительным к действию инсулина, что также приводит к повышению уровня глюкозы в крови. Однако, в отличие от диабета 1-го типа, поджелудочная железа продолжает вырабатывать инсулин. В третьем сценарии коэффициент K 6 снижен в 6 раз, это означает, что утилизация глюкозы инсулином нарушена на 83 %.

• 4.    В четвертом сценарии рассматривается процесс в отсутствии функциональных нарушений, при этом функция поступления углеводов в кровь f ( t ) отличается от первых трех сценариев и характеризует потребление быстрых углеводов.

В результате идентификации параметров в первом приближении планируется использовать некоторые осредненные коэффициенты, характеризующие углеводный обмен в норме. На данном этапе работы коэффициенты модели подобраны таким образом, чтобы в базовом сценарии при отсутствии нарушений в организме и сбалансированном питании концентрации инсулина и глюкозы были в пределах физиологической нормы. В табл. 3 приведены параметры модели для всех четырех сценариев. В первом приближении f (t) рассматривается как функция поступления глюкозы в кровь из желудочно-кишечного тракта в зависимости от времени и

Таблица 3

Значения параметров модели

Параметр	Значение	Размерность	Параметр	Значение (сценарий 1–3; сценарий 4)	Размерность
Индивидуальные коэффициенты			Параметры функции поступления глюкозы
K 1	1,00E-05	1/с	f 1max	1,10E-02; 2,20E-02	ммоль/(с∙л)
K 2	2,00E-03	л∙мкЕд /(с ∙ ммоль2)	f 2max	1,30E-02; 4E-02	ммоль/(с∙л)
			3max	1,20E-02; 3,7E-02	ммоль/(с∙л)
K 3	5,00E-03	1/с	a 0	1,02E-03; 2,8E-07	ммоль/(с2∙л)
			b 0	-6,16E-01; -2,36	ммоль/(с∙л)
K 4	3,0E-03	1/с	a 1	1,02E-03; 2,2E-02	ммоль/(с2∙л)
K 5	1,00E-03	л/(с ∙ ммоль)	b 1	-6,16E-01; -1,76E-01	ммоль/(с∙л)
K 6	3,00E-04	ммоль/(с ∙ мкЕд)	a 2	5,50E-03; 3,37E+05	ммоль/(с2∙л)
K 7	4	ммоль/л	b 2	-4,40E-02; -1,84	ммоль/(с∙л)
K 8	9,00E-03	(ммоль2 ∙ мкЕд) /(с ∙ л3)	a 3	3,37; 4E-02	ммоль/(с2∙л)
K 9	1,00E-04	1/с	b 3	-5,73E-01; -5,2E-01	ммоль/(с∙л)
			a 4	5,51E-03; 2,59E+13	ммоль/(с2∙л)
			b 4	-6,97E-02; -2,44	ммоль/(с∙л)
K 10	2,70E-03	ммоль/(с ∙ л)	a 5	2,44E+02; 3,7E-02	ммоль/(с2∙л)
			b 5	-6,56E-01; -6,66E-01	ммоль/(с∙л)
			a 6	5,09E-03; 1E+18	ммоль/(с2∙л)
			b 6	-8,98E-02; -2,36	ммоль/(с∙л)

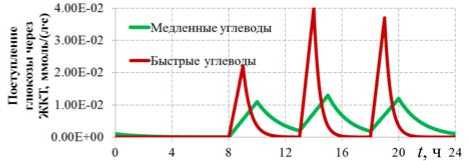
Рис. 3. График функции поступления глюкозы в кровь из желудочно-кишечного тракта f (t)

определяется кусочно-заданной функцией: линейным уравнением при возрастающем потоке ( f (t) = at + b ) и экспоненциальным уравнением при убывающем потоке ( f (t) = ae^bt ). На рис. 3 приведен график функции, соответствующий трем приемам пищи. Параметры f_{i max} в табл. 1 соответствуют максимальным значениям функции f (t) после i -го приема пищи.

В первых трех сценариях максимальные значения fi max близки для всех приемов пищи, что характеризует более равномерное поступление углеводов в кровь, при этом пиковые значения функции достигаются через 2 ч после приема пищи, а еще через 2 ч функция поступления углеводов приближается к 0. Подобный паттерн характерен при потреблении медленных углеводов. В четвертом сценарии поступление углеводов в кровь во время приемов пищи менее сбалансированно, в первый прием пищи (завтрак) поступает наименьшее количество, а во второй и третий прием (обед и ужин) – в разы больше, при этом пиковые значения достигаются через час после приема пищи, а еще через час наблюдается значительное истощение потока углеводов в кровь. Более кратковременные пики с большей амплитудой характерны при употреблении быстрых углеводов. При заданных параметрах общий поток углеводов из крови в ЖКТ для всех сценариев составляет около 305 г за 24 ч, что соответствует средним нормативам потребления.

На данном этапе для каждого из трех сценариев в модели заданы одинаковые начальные условия: C _г ^к _л ^р ( t = 0) = 4,5 ммоль/л; C _и ^к _н ^р _с ( t = 0) = 2,6 мкЕд/мл; C _г ^п _л ^еч ( t = 0) = 400 ммоль/л; C _г ^к _н ^р ( t = 0) = 3 ммоль/л. Времена запаздывания t ₁, t ₂, t ₃ принимаются равными 60 с, t 4 , t 5 = 180 с, t 6 , t 7 = 240 с.

Для численного решения системы уравнений используется метод Эйлера с шагом по времени, равным 4 с. Результаты получены для временного интервала от 0 до 24 ч. На рис. 4 приведены результаты расчетов для всех четырех сценариев.

На рис. 4, а , представлено сравнение сценариев, в которых рассматривается динамика концентрации глюкозы. Пики, наблюдаемые на графиках, соответствуют моментам приема пищи. Максимальное увеличение уровня глюкозы наблюдается во время обеда (около 13–14 ч), что соответствует пику поступления углеводов из ЖКТ. В первом сценарии уровень глюкозы достигает 8,2 ммоль/л и быстрее снижается в район нормативных значений. Во втором сценарии при сахарном диабете 1-го типа пиковые значения достигают 10,8 ммоль/л, а в третьем сценарии – 8,8 ммоль/л. При наличии диабета времена повышенного содержания глюкозы в крови (более 7 ммоль/л), а также сами уровни превышения больше, чем при отсутствии заболевания, что увеличивает риски развития сопутствующих заболеваний

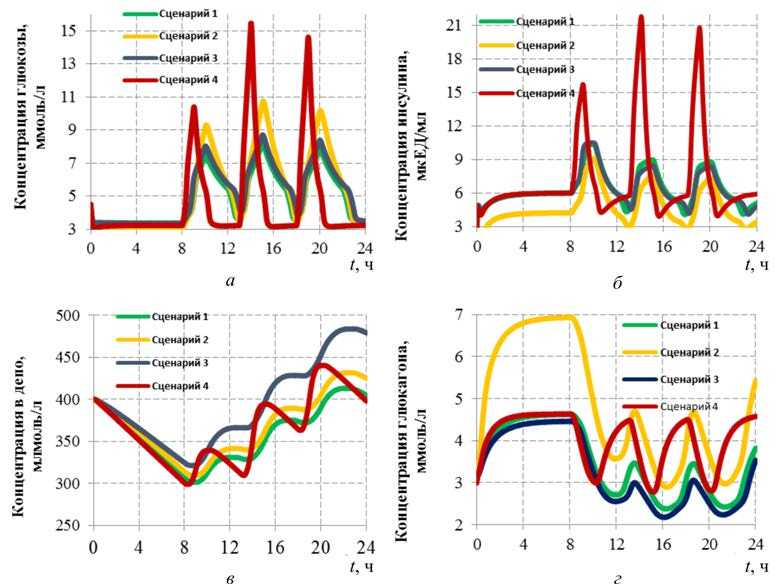
Рис. 4. Результаты численного моделирования

и осложнений. В четвертом сценарии пиковые значения глюкозы достигают 15,5 ммоль/л, что намного превышает значения в предыдущих сценариях. Несмотря на более кратковременный рост уровня глюкозы, полученные значения являются критическими (более 11 ммоль/л) и могут вызвать значительное повреждение сосудов. Таким образом, в сценариях 1–3 сбалансированное в течение дня поступление медленных углеводов способствует не такому значительному росту концентраций глюкозы даже при наличии диабета. При несбалансированном употреблении быстрых углеводов, например, фастфуда, особенно с увеличением калорийности в один из приемов пищи относительно других, даже при текущем отсутствии заболеваний и соблюдении суточных норм по углеводам в целом, наблюдаются повышающие риски здоровью уровни глюкозы в крови. В случае наличия заболеваний при таком режиме питания следует ожидать еще большего повышения уровня глюкозы и ситуация будет усугубляться.

Рис. 4, б, демонстрирует динамику концентрации инсулина в крови. В сценарии 1 выработка и действие инсулина находятся в равновесии, и концентрация соответствует физиологической норме. В сценарии 2 концентрация инсулина значительно снижена и колеблется в диапазоне от 0,3 до 9 мкЕД/мл, слабо реагирует на прием пищи. Такое состояние вызвано сахарным диабетом 1-го типа. В сценарии 3 выработка инсулина не нарушена и график практически совпадает с графиком сценария 1 в отсутствии заболевания. Максимум концентрации инсулина дос- тигает пика около 10,6 мкЕД/мл в третьем сценарии (в первом – 10,2 мкЕД/мл), что соответствует нормальной реакции организма. Некоторое повышение инсулина связано с тем, что организм пытается компенсировать высокий уровень сахара в крови, вырабатывая больше инсулина, чем необходимо в сценарии 3. Однако из-за резистентности клеток к инсулину его действие оказывается неэффективным, и уровень глюкозы в крови остается высоким. В сценарии 4 в ответ на более высокие значения глюкозы концентрация инсулина также повышается до 21,3 ммоль/л, что в целом соответствует адекватной реакции в здоровом организме.

Рис. 4, в, представляет собой изменение концентрации глюкозы в печени (депо). В первые 8 ч (в период сна) поток глюкозы идет из печени в кровь для поддержания уровня глюкозы в норме. Однако с 9 до 24 ч ситуация начинает меняться – уровень глюкозы в печени начинает увеличиваться. Это происходит из-за того, что печень активно запасает глюкозу в виде гликогена, реагируя на превышение порогового уровня глюкозы в крови. После 24 ч наблюдается стабилизация концентрации глюкозы в печени, которая возвращается к исходному уровню в сценарии 1, 4. В данном случае при отсутствии нарушений в организме наблюдается углеводный баланс. Важно отметить, что в сценариях 2 и 3 уровень глюкозы в крови превышает нормальные значения. Перенасыщение глюкозой приводит к тому, что организм начинает откладывать избыточное количество глюкозы в печени, увеличивая концентрацию в депо к концу дня на 25 и 80 ммоль/л соответственно в сценариях 2 и 3. Депо в печени имеет пределы накопления, и при каждодневном повторении такой ситуации следует ожидать, что избытки углеводов очень быстро начнут преобразовываться в жиры, повышая риски возникновения ожирения. Подобная ситуация будет развиваться и при отсутствии функциональных нарушений в случае увеличения функции поступления углеводов f (t). В сценарии 4 в отсутствии нарушений организм справляется с поддержанием углеводного баланса, в этом случае фактором риска выступает только высокой уровень глюкозы. Анализ современных данных литературы показал, что высокая доля углеводов в рационе является частой причиной ожирения, диабета и связанных с ними кардиометаболических заболеваний. Наиболее часто возникновение ожирения ассоциировано именно с диабетом 2-го типа, что подтверждает полученные результаты по большему накоплению запасов в сценарии 3. Высокое потребление углеводов вызывает эндокринную дерегуляцию, характеризующуюся гиперинсулинемией, что приводит к разделению энергии с увеличением запаса жировой массы [21, 22]. Контроль калорийности питания и снижение потребления сахара достоверно приводит к уменьшению распространенности в популяции случаев болезней системы кровообращения и смертности [23, 24].

Рис. 4, г, иллюстрирует динамику концентрации глюкагона в крови. В первом и третьем сценариях, отражающих нормальную выработку инсулина, уровни глюкагона практически идентичны, варьируясь от минимальных значений в 2,2 ммоль/л до максимальных в 4,7 ммоль/л в течение дня. В отличие от них, второй сценарий характеризуется значительно повышенной концентрацией глюкагона в крови до 6,9 ммоль/л. При дефиците инсулина наблюдается компенсаторное усиление образования глюкагона, что, в свою очередь, способствует гипергликемии. В сценарии 4 уровни глюкагона повышаются до 4,5 ммоль/л из-за более быстрого снижения концентрации глюкозы в крови и необходимости стимулирования высвобождения сахара из печени. В отсутствии внешнего источника с 0 до 8 ч решение системы приближается к стационарному состоянию, за исключением концентрации в депо, которая в это время снижается. Уровень глюкагона в крови понижается после приема пищи, что согласуется с известными литературными данными: в физиологических условиях после приема пищи, когда уровень глюкозы и инсулина повышается, концентрация глюкагона плавно снижается на 30–40 % от базального уровня [25]. Напротив, в период голодания отмечается постепенное увеличение секреции глюкагона на 50–70 %. Такая сбалансированная регуляция обеспечивает поддержание стабильного уровня глюкозы в пределах физиологической нормы (4–5,5 ммоль/л)8 [26, 27].

Полученную модель можно использовать для прогнозирования индивидуального риска здоровью, связанного со значениями концентрации глюкозы в крови и временем ее повышения относительно нормальных значений при различных режимах питания (фастфуд, высококалорийная пища, несбалансированное в течение суток питание). В зависимости от получаемых результатов в качестве мер профилактики заболеваний могут быть подобраны оптимальные индивидуальные рекомендации по балансировке количества потребляемых углеводов и приемов пищи в течение дня.

Выводы. Разработана новая математическая модель, описывающая регуляцию углеводного обмена, которая позволяет прогнозировать уровень глюкозы в крови как основного риск-индуцирую-щего фактора риска при различной пищевой нагрузке с учетом индивидуальных заболеваний органов пищеварительной системы. Результаты численного моделирования демонстрируют стабильное поддержание уровня глюкозы при нормальном обмене и сбалансированном потреблении медленных углеводов, а также отклонение от нормы при наличии диабета и при несбалансированном во времени поступлении быстрых углеводов, что позволяет лучше понять динамику метаболических изменений в организме.

Разработанные подходы могут стать основой для дальнейших исследований в этой области и способствовать разработке более эффективных методов профилактики заболеваний, связанных с нарушением углеводного обмена и болезнями поджелудочной железы. В дальнейших исследованиях целесообразно рассмотреть углеводный обмен в совокупности с жировым, что позволит более детально учесть механизмы развития диабета и сопутствующих патологий.

Финансирование. Результаты получены при выполнении государственного задания Министерства науки и высшего образования Российской Федерации на выполнение фундаментальных научных исследований (проект FSNM-2025-0001).