Математическая модель реологического поведения вязкопластической жидкости, которая демонстрирует проявление эффекта “отвердевания”

Такое поведение рассматриваемых материалов можно интерпретировать, как проявление эффекта “отвердевания” [2-4]. Известны примеры практического применения таких вязкопластических материалов [5], демонстрирующих эффект “отвердевания”. В [6] на уровне соответствующего механического аналога указывалось на возможность построения реологической модели вязкопластических жидкостей, которые могут также демонстрировать и проявление эффекта “отвердевания”.

Далее представлена реологическая модель вязкопластической жидкости, демонстрирующей проявление эффекта “отвердевания”. Рассмотрим, прежде всего, сдвиговое виско-зиметрическое течение с одной, тождественно не равной нулю, составляющей скорости.

Качественно, зависимость касательного напряжения т(|у|) от скорости сдвига у для материалов с указанным выше реологическим поведением должна иметь вид, представленный на рисунке 1.

Особенности такой кривой течения за ключаются в следующем.

До тех пор, пока выполняется условие |т| < т0, скорость сдвига равняется нулю (деформирование отсутствует). В этом диапазоне изменения касательного напряжения материал должен вести себя подобно твердому телу.

При превышении же модулем касатель ного напряжения соответствующего порогового значения т0 > 0 начинается процесс течения (деформирования). При этом связь между |т| и |/| должна иметь нелинейный характер, поскольку при приближении скорости сдвига к некоторому критическому значению (|/| ^ Yi), крутизна кривой течения должна неограни ченно возрастать:

lim <

Y ^ Y

d к И ) d \г\

> = да .

Поскольку крутизна кривой течения характеризует, вообще говоря, эффективную вязкость Mef жидкости, такой характер зависимости т(/|), связанный с неограниченным возрастанием ^eff, и можно интерпретировать, как проявление эффекта “отвердевания”.

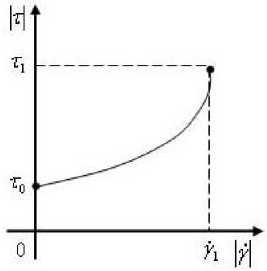
Рисунок 1. Характер кривой течения для вязкопластических материалов с эффектом “отвердевания”.

Таким образом, собственно течение будет иметь место лишь в тех зонах области, заполненной рассматриваемой жидкостью, где выполняется условие:

^т о <  И <  ^т 1 . ⁽²⁾

Все вышеизложенное означает, что в той области, где находится жидкость, наряду с зоной течения могут иметь место и зоны, в которых жидкость ведет себя подобно твердому телу. Причем, эти зоны могут быть двух типов.

Жесткие зоны первого типа должны быть обусловлены пластическими свойствами материала. На границе этих жестких зон с зоной течения выполняется условие Ц = т ₀.

Жесткие зоны второго типа должны быть обусловлены проявлением эффекта “отвердевания” и на их границах с зоной течения должно выполняться условие Ц = т 1 .

Учитывая, что, априори, предполагается выполнение неравенства т ₀ <  т ₁, жесткие зоны первого и второго типов всегда должны быть разделены зоной течения.

Все эти особенности механического поведения сплошных сред такого рода можно для диапазона (2) описать в рамках реологического соотношения:

тт = A + B. (Y1 - jf))n. (3)

Константы A и B определяются с учетом удовлетворения следующим условиям:

тт( 0) =т о; К Y1) = т и могут быть представлены через основные реологические параметры модели следующим образом:

A = т^ B = - ( т - т 0 ) • Y — ⁿ . (4)

В соотношении (3) предполагается, что на реологическую константу n накладывается ограничение вида:

0 <  n <  1.

Последнее условие заведомо обеспечивает выполнение (1) при | / | ^ Д и, соответственно, моделирование эффекта “отвердевания”.

Характер влияния реологической кон

станты n на кривые течения, построенные в

безразмерных координатах:

| ф Й-И ;  „ 1 = И , т1 - т 0             Y1

иллюстрируют данные, представленные на рисунке 2. В соотношениях (5) и далее верхним штрихом отмечены безразмерные величины.

На рисунке 3 линия \у ' | = 1 является вертикальной асимптотой к графикам зависимости эффективной вязкости от модуля скорости сдвига.

Проведенное рассмотрение для простейшего вискозиметрического течения с одной, тождественно не равной нулю, составляющей скорости приводит к следующей реологической модели вязко-пластической жидкости с четырьмя константами n , / 1 , т ₀, т 1 , которая демон

стрирует проявление эффекта “отвердевания”:

0 ;

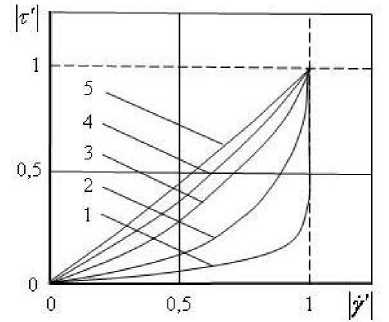
Рисунок 2. Влияние параметра n на кривые течения вязко-пластической жидкости с эффектом “отвердевания”: n = 0.1 (1); 0.3 (2); 0.5 (3); 0.7 (4); 0.9 (5).

I Y = 1

1 -

V ^т 1

^т 1

-

-

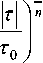
I ^т 1 < ^т 0 ;

• Д ; т 0 <  ^ <  т ;

Рассмотрим теперь обобщение предложенного соотношения (3) с учетом (4) на случай произвольного течения.

Наиболее часто модель нелинейновязкой жидкости на уровне связи между компонентами тензоров напряжений и скоростей деформаций представляют в форме:

т у =- P • 8 j + 2 • m ( 1 2 ) • S ij ;     i , j = 1,2,3 ;      (6)

I 2 = ^S 11 • ^S 22 ^{+ S} 22 • ^S 33 ^{+ S} 33 • ^S 11 ^{- S} \₂ ^{- S} 2₃ ^{- S} 3P

Влияние этого же параметра на безразмерную эффективную вязкость:

^eff =

^ eff

M s

d т

Mf = dY;

^T 1 ^{- T} 0

Y 1

можно проследить по зависимостям, представленным графически на рисунке 3. Здесь M S представляет собой принимаемое в качестве масштабного значение динамической вязкости.

где т ij , S ij - компоненты тензоров напряжений и скоростей деформаций, соответственно; P -давление; 8 у - символ Кронекера; м ( 1 2 ) -функция второго инварианта 1 2 тензора скоростей деформаций.

Принимая за основу выражение (3), с учетом (4) можно для зоны течения вязкопластической жидкости с эффектом “отвердевания” в общем случае предложить следующее соотношени е:

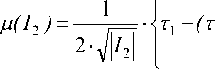
^-т 0 ) •

(

V

I

^ I 2 crit

n

^ ;(7)

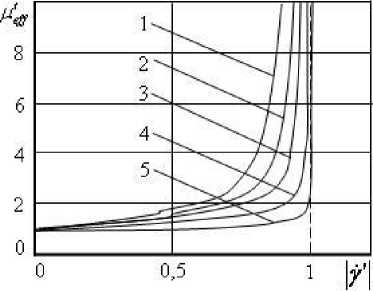
Рисунок 3. Влияние параметра n на эффективную вязкость: n = 0.1 (1); 0.3 (2); 0.5 (3); 0.7 (4); 0.9 (5).

|д|<д ., 2         2 crit-

где I _{2 crit} - критическое значение модуля второго инварианта тензора скоростей деформаций, при приближении к которому ( \l ₂ 1 ^ I _{2 crit} ) начинает проявляться эффект “отвердевания”.

Заметим, что в частном случае простейших вискозиметрических течений, когда: Y = ² • ^S ; 1 2 =^{-S 2} =^{- 1} • у ²; Y 1 = 2 • .Jl^ , соотношения (6), (7) трансформируются к виду (3) с учетом (4). Здесь S - единственная, тождественно не равная нулю, составляющая тензора скоростей деформаций.

Естественно, что параметр I _{2 ,crit} следует рассматривать, как самостоятельную реологическую константу, характеризующую поведение конкретной жидкости. Эта константа, как и три другие n , τ ₀ , τ ₁ должна определяться на основе обработки соответствующих экспериментальных данных.