Математическая модель решения обратной задачи геометрической оптики в профилометрии протяженных внутренних отражающих поверхностей

Детали с протяженными внутренними поверхностями широко распространены во всех областях техники. Под протяженной поверхностью мы будем понимать поверхность, длина продольного профиля которой как минимум на порядок превышает характеристические размеры ее поперечного сечения которой. Форма профилей протяженных внутренних поверхностей труб, гидро- и пневмоцилиндров, цилиндров двигателей внутреннего сгорания, волноводов, каналов охлаждения и смазки и т.п. определяет технические и эксплуатационные характеристики устройств с такими узлами и деталями. Измерение профилей протяженных внутренних поверхностей необходимо на всех этапах жизненного цикла изделий. Однако проблема измерения профилей протяженных внутренних поверхностей до сих пор не решена.

Механические [Антоненкои др., 2009], оптико-механические, пневматические и гидравлические методы измерения либо не дают полную и достоверную информацию о продольных и поперечных профилях протяженной внутренней поверхности, либо имеют низкую производительность измерений. Измерительные приборы, как правило, хрупки и дороги. Кроме того, все эти методы являются контактными, что дополнительно снижает сферу их применимости.

Оптические методы (стереоскопические [Родэ и др., 2007; Лапа, Браилов, 2014], интерференционные [Вишняков, Левин, 2011], растровые [Ефанов и др., 2006; Сивохин, Кузнецов 2012]) являются бесконтактными и могут обеспечить необходимую точность измерений полноту измерительной информации. Однако они трудноприменимы или неприменимы для измерения протяженных внутренних поверхностей. Кроме того, для восстановления профилей поверхности они требуют сложной математической обработки измерительной информации.

В работе [Каралаш и др., 2015] описан оптико-электронный метод измерения профилометрии протяженных внутренних цилиндрических поверхностей (ОЭМИ), основанный на математической модели отражения света от протяженной внутренней цилиндрической поверхности в приближении геометрической оптики. Метод обеспечивает бесконтактное снятие измерительной информации и не требует сложной обработки и интерпретации интерференционных полей или муаровых картин. В результате ОЭМИ превосходит традиционные методы измерения по достоверности, точности и производительности.

На Рис. 1 представлена оптическая схема снятия измерительной информации. Исследуемая поверхность освещается пространственно модулированным световым потоком. Свет, отраженный от поверхности, регистрируется цифровой телевизионной системой

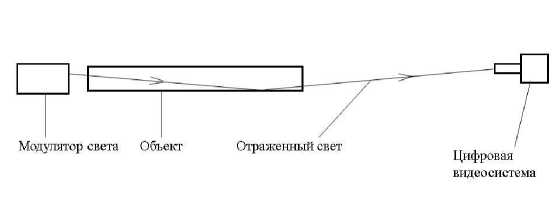
Рис. 1. Оптическая схема ОЭМИ.

Пространственная модуляция отраженного пучка определяется как видом исходной модуляции, так и формой исследуемой поверхности.

Вычисление параметров оптической системы исходя из характеристик, входящих и выходящих световых пучков - классическая обратная задача оптики. Как известно, в общем случае эта задача не имеет единственного решения. Тем не менее, для случая цилиндрической поверхности и поверхности с малыми отклонениями от номинального цилиндра разработана методика, позволяющая однозначно интерпретировать ход лучей в оптической системе и найти приближенное решение обратной задачи оптики.

В настоящей работе предпринята попытка найти условия разрешимости обратной задачи оптики для случая отражения света от протяженной внутренней поверхности не обязательно цилиндрической.

На Рис.2 схематически представлен ход лучей при отражении света от протяженной внутренней поверхности.

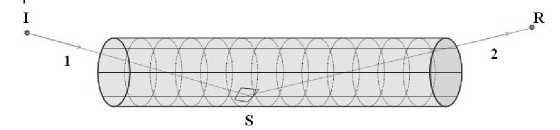
Рис. 2. ‘

Рис. 2.Ход лучей при отражении света от протяженной внутренней поверхности. I – источник света, 1 – падающий луч, 2 – отраженный луч, R – зрачок фоторегистратора, S – элемент поверхности в точке падения луча

Падающий луч (1) и луч отраженный (2) теоретически должны пересекаться в одной точке — точке отражения от поверхности (S), поэтому, зная координаты источника света (I) и зрачка фоторегистратора (R), а также зная углы, под которыми луч (1) вышел из источника и под которыми луч (2) попал в зрачок приемника, можно однозначно определить координаты точки отражения света S и вектор нормали к отражающей поверхности в этой точке. На практике ситуация отличается от теории, по крайней мере, в трех аспектах. Во-первых, все экспериментально измеряемые параметры оптической системы известны с некоторой погрешностью. Во-вторых, лучи имеют ненулевое сечение и ненулевой угол расходимости, вследствие чего падающий луч засвечивает на поверхности не точку, а пятно, вытянутое параллельно оси поверхности. В-третьих, сама поверхность имеет как мелкие шероховатости, так и протяженные отклонения от идеальной формы. Поэтому требуется построение регуляризирующей процедуры, сводящей к минимуму влияние случайных факторов на конечный результат.

Используя направляющие орты (V 1 ) и (N _f ) лучей (1) и (2) и вычисляя их векторное произведение, можно построить перпендикулярный им отрезок (ZP). Далее, принимаем середину (Q) это отрезказа первое приближение точки пересечения падающего (1) и отраженного (2) лучей. Далее проводим плоскость (Рг) через конечную точку расположения источника (I ), точку расположения зрачка фоторегистратора (Я) и точку Q, а затем строим ортогональные проекции (Я 1 ) и (Я ₂ ) лучей (1) и (2) соответственно. Орту (V) биссектрисы угла между (R1) и (R2), исходящую из точки Q, принимаем за нормаль к отражающей поверхности. Следуя описанной стратегии, предъявим явные вычислительные формулы.

Пусть заданы две прямые своими уравнениями в каноническом виде х — а1

^L i ^: к------- bi — Qi

У -	— Q f	z — а з	х -	- с 1
b f	— Q f	и L f . Ьз — а з	А 1	— С 1

У — С ₂ _ z — С з

Af — С2    Аз — С3 ’ которые имеют направляющие векторы:

s t ^{_ (b} i ^— Q i , ^b 2 ^— й2, ^ь з ^— а з ) ^{_ (l} i , Z ₂ , ¹ з ⁾

s t ⁼ (А 1 — С 1 , A f — С 2 , А з — С з ) _ (k ₁ ,k f ,kз')

Вектор, перпендикулярный обеим прямым, может быть определен как векторное произведе- ние направляющих:

^ _ [s t , s f ] _

-→ г ki li

-→ 3 ^k f l f

^ ^к з ¹ з

^{_ г} (^з ^{— к}зУ + ^{3 (} к з ! 1 ^— W + ^{3 (k} i ^l f ^— k f l i ) ^_

_ — _х

-→     -→ -→ г + —у 3 + —z к

Уравнение плоскости, которая проходит через прямую L _f параллельно вектору п , имеет в качестве вектора нормали вектор — р , являющийся результатом двойного векторного произведения векторов s f , [s t , s t ]:

—Р _[st, [st, st]]_ г              3              к

_      ki           kf           кз      _ lfkз — lзkf —11кз + 1зк1 li kf — lfki

_ г (k f l i k f — k f l f k i + k з l 1 k з — k з l з k 1 ) —

^{— 3 (к} 1 ^l 1 ^k f ^{— k} 1 ^l 2 ^k 1 ^{— k} 3 ^l 2 ^k 3 + ^k 3 ^l 3 ^k 2 ⁾ +

+к (k 1 l з k 1 — k 1 l 1 k з — k 2 l 2 k з + k 2 l з k 2 ) .

Уравнение плоскости, которая проходит через точку С (С 1 , с ₂ ,сз ) параллельно вектору — ^ , может быть задано в следующем виде:

Р 1 : п _{Р т} (х — c i ) + п _{Р у} (у — C f ) + п _{Р г} (z — С з ) _ 0

или

Р1 : —р^х + —руу + —ргz — Dp _ 0, при Dp _ —Ррсci + —ру Cf + —рг Сз).

Запишем прямую L 1 в параметрическом виде. Затем, подставив значения x,y,z в уравнение плоскости, найдем точку их пересечения.

t i

х — а1    у — af    z — аз bi — Qi    bf — af    Ьз — аз

Х1 — й 1 + t 1 (b 1 — ^ i )

У 1 ^{— й} 2 ^{+ t} 1 ^(k 2 ^{— й} 2 ) ^z 1 ^— Й 3 + Ь 1 ⁽ Ь з ^— й з )

^П р _т ^(й 1 ^{+ t} 1 ⁽^ 1 ^{— й} 1 )) ^{+ П} р _у ^(й 2 ^{+ t} 1 ⁽^ 2 ^{— й} 2 ^{)) + П} рг ^(й 3 ^{+ t} 1 ⁽^ 3 ^{— й} 3 )) ^— D p ^— 0

Полученное уравнение является линейным относительно t 1 , откуда легко можно получить:

t _—          П р _т й 1 + П р у й 2 + П р , й з + D p

^П р _т ⁽^ 1 ^{— й} 1 ) ^{+ П} р _у ⁽^ 2 ^{— й} 2 ) ^{+ П} р , ⁽^ 3 ^{— й} 3 )

Далее определим точку N 1 (x 1 , у 1 , z 1 ).

Аналогичным образом, найдем координаты второй точки. Уравнение плоскости, которая проходит через прямую L1 параллельно вектору it имеет нормальным вектор t = 1, [1, 122]] .

j            к

^ 2                   ^ 3

1 з ^к 2  ^—кцк з ⁺ 1 з ^к 1   1 1 ^к 2 ^— ^ 2 ^к 1

t —

1 2 к з

г

^— г ⁽/ 2 ? 1 ^к 2 ^— / 2 ? 2 ^к 1 ⁺ 1 з 1 1 ^к 3 ^— / з ^ 3 ^к 1 ) ^—

^{— j} (М 1 ^к 2 ^— ^2 ^к 1 ^— ^2 ^к 3 ⁺ 1 з 1 з ^к 2 ) ⁺

+к (1 1 1 з к 1 — 1 1 1 1 к з — / 2 / 2 к з + 1 2 1 з к 2 ) .

По аналогии, уравнение плоскости, которая проходит через точку А(й 1 ,й ₂ ,й з ) параллельно вектору п р :

Р 1 : п. (х — й 1 ) + П р ^ (у — Й 2 ) + П р , (z - й з ) — 0

Р 1 : П р ^ х + П р _у у + П р , z — D p — 0, при D p — (п р ^ й 1 + П р _у й 2 + П р , йз)

Запишем прямую L 2 в параметрическом виде, подставив значения x,y,z в уравнение плоскости, найдем точку их пересечения.

_t = х — € 1 _— у — С 2 _— z — С 3

^ 1 — С 1    ^ 2 — С 2     ^ 3 — С з

{ Х 2 — С 1 + t 2 (^ 1 — С 1 )

У 2 — С 2 + t 2 (^ 2 — С 2 )

z 2 — С 3 + t 2 (^ 3 — С 3 )

^П р $ ^{( с} 1 ^{+ t} 2 ⁽^ 1 ^{— С} 1 )) ^{+ П} р _у ^{( с} 2 ^{+ t} 2 ⁽^ 2 ^{— С} 2 )) ^{+ П} р _г ^{( с} З ^{+ t} 2 ⁽^ 3 ^{— С} 3 )) ^{— D} Р ^{— 0}

Рассчитаем значение t ₂ при х ₂ , y ₂ ,z ₂ :

_______ П р _т С 1 + П р _у С 2 + П р , С з + Dp _______ П р _т (^ 1 — С 1 ) + П р у (^ 2 — С 2 ) + П р , (й з — С з )

Далее определим точку N ₂ (х ₂ ,у ₂ , z ₂ ).

Найдем координаты середины отрезка N 1 N 2

N Х²^ ^у^^ ,^z 2+₂. ^ _=Лу х _с ,у _с _z _c )

Построим плоскость W через точки A, D, N _c :

Напишем определитель:

W —

х — Й 1

х _с — Й 1

й 1 — й 1

У ^{— й} 2

У с — й 2

^ 2 — Й 2

z — й з z c — й з ^й з ^{— й} з

х — й 1	У — й 2	z — й з
т 1	m 2	т з
9 1	9 2	9 з

= (ж - а х ) (т 2 9 з - 9 2 ^ 3 ) + (у - < 2 ) (т з 9 х - т х 9 з ) + (z - 1 3 ) (т х 9 2 - 9 х т 2 )

= ж (т 2 9 з - 9 2Г П 3 ) + у (m 3 9 1 - т х 9 3 ) + z (т х 9 2 - 9 1 m 2 ) - (а _х (т 2 9 з - 9 2 т з ) + < 2 (т з 9 1 - т х 9 з ) + + а з (т х 9 2 - 9 х т 2 ))

Равенство нулю (W = 0), которого дает искомую плоскость.

В этой плоскости лежат прямые N _C D и N _C A, которые являются проекциями для CD и AB соответственно. Сумма нормированных направляющих векторов N _C D и N _C A дает биссектрису, направление которой совпадает с нормалью к идеальной отражающей поверхности.

Пусть входная система представляет собой квадратную матрицу падающих лучей I размерностью (п х п) . Тогда выходная система также представляет собой квадратную матрицу отраженных лучей J той же размерности.

Применяя к каждой паре лучей описанное выше преобразование, получаем локальное описание освещенного участка поверхности в виде матрицы R координат отражающих точек и нормалей к поверхности в этих точках.

Сдвигая группу излучающих элементов и, соответственно, матрицу I , можно провести сканирование всей поверхности и получить набор перекрывающихся матриц R ^ , описывающих всю исследуемую поверхность. Перекрытие матриц позволяет применить методики скользящего среднего при вычислении координат и нормалей, а также оценить дисперсию измеренных величин. Таким образом появляется возможность уменьшения погрешности измерений, вносимых неоднозначностью определения нормалей при наличии микрорельефа, формирующего диффузное отражение света.

Сканируя внутреннюю поверхность от левого ее торца к правому (см. рис. 2), мы получим набор координат и нормалей для набора точек поверхности, количество и взаимное расположение которых определяется как взаимным расположением источника и приемника света, так и угловым шагом сканирования. В случае протяженной внутренней поверхности углы между падающим лучом и нормаль к поверхности близок к прямому, поэтому при ненулевом сечении луча длина светового пятна в продольном направлении больше диаметра луча, соотношение длины пятна и диаметра луча в среднем составляет величину порядка отношения длины поверхности к размеру ее поперечного сечения, но меняется от точки к точке вместе с изменением угла падения луча. Расстояние между центрами световых пятен также меняются от точки к точке даже при постоянном угловом шаге сканирования. Тем не менее, на основе полученного массива координат и нормалей форма внутренней протяженной поверхности может быть интерполирована и визуализирована в виде 3-d модели.

Разработан комплекс программ, реализующий описанные алгоритмы получения и обработки измерительной информации. Открытым пока остается вопрос о выборе метода сканирования протяженной внутренней поверхности. На первый взгляд, наилучшие результаты должно было бы дать сканирование поверхности лазерным лучом, поскольку он обладает малой расходимостью, что обеспечивает более точное определение координат точки отражения, и высокой яркостью, что упрощает задачу регистрации отраженного света. Однако когерентность лазерного света при отражении его от реальной поверхности с макро и микронеровностями приводит к появлению в плоскости зрачка фоторегистратора диффузной спекл-картины [Jacquot, 2008], что не позволяет однозначно определить угол отраженного луча и вносит недопустимо большие ошибки в определение координат и нормалей точек поверхности. В связи с этим, более перспективным представляется использование некогерентных источников света. В настоящее время авторами теоретически разрабатываются и моделируются возможные оптико-механические схемы сканирующих систем с некогерентными источниками света.

Полученные в работе результаты найдут применение в системах контроля качества изготовления деталей и узлов с протяженными внутренними поверхностями, при оценке технического состояния таких узлов и деталей в процессе их эксплуатации и при оценке их остаточного ресурса.