Математическая модель шероховатой поверхности контактного трибосопряжения

В подвижных контактных трибосопряжениях, работающих в условиях граничной смазки и внешнего трения, наиболее распространено абразивно-усталостное изнашивание, возникающее при многократном деформировании поверхностных слоев [1]. На деформацию поверхностных слоев существенное влияние оказывает тепловое и напряженное состояние в зоне контакта, зависящее от геометрических параметров микронеровностей контактной поверхности, режима нагружения и механических свойств тел трения.

В поверхностном слое, вследствие высокой концентрации энергии трения возникают градиенты температуры, деформаций и напряжений, определяемые по результатам конечноэлементного анализа температурного и напряженно-деформированного состояния элементов трибосистемы. Оценку температурного и напряженно-деформированного состояния элементов сопряжения с учетом реального микрорельефа трущихся поверхностей подвижного контакта целесообразно выполнять на различных уровнях представления объекта с выделением соответственно микро-, субмакро- и макроуровней.

В качестве примера рассмотрим высоконагруженное подвижное контактное сопряжение с композиционным смазочным материалом в виде графито-масляных макродепо, выполненных в плоской платформе (рис. 1).

Пятна фактического контакта

б)                            в)                    х

Рис. 1. Представление элемента контактного трибосопряжения с выделением конкретных объектов на уровнях: а - макро, б - субмакро, в - микро

На макроуровне представления поверхности трения (см. рис. 1, а) рассматриваются вопросы структурной оптимизации отдельных элементов и взаимодействие трибосистемы с окружающей средой. На субмакроуровне (см. рис. 1, б) конкретизируются граничные условия задач теплопроводности и контактного теплообмена, а на микроуровне (см. рис. 1, в), методами математической

Лазарев В.Е., Грамм М.И., Лазарев Е.А., Лаврик А.Н. Математическая модель шероховатой Franek F., Pauschitz A., Voriaufer G., Jisa R.поверхности контактного трибосопряжения статистики описывается топографическая структура поверхности с оценкой суммарного значения функции спектральной плотности, как основного критерия энергетической насыщенности и решаются задачи контактного анализа.

При создании математической модели шероховатой поверхности на микроуровне особую важность представляет процедура ее симплификации (упрощения), поскольку профилограмма поверхности в оригинальном виде сложна для дискретизации в виде конечно-элементной сетки из-за непредсказуемости рельефа и трудностей его математического описания [2]. Создание конечно-элементных моделей субмакро- и, особенно, макроуровней также затруднено спецификой формирования множества конечных элементов достаточно малых размеров для описания микрорельефа шероховатости значительной протяженности и ограниченными в этой связи вычислительными возможностями ЭВМ.

Получаемые в результате конечно-элементного анализа параметры температурного и напряженно-деформированного состояния элемента подвижного трибосопряжения, содержащего фрагмент шероховатой поверхности, например размерами 80x80 мкм, нуждаются в экспериментальной проверке, в частности уровня температуры в реперных точках. Использование в этих целях моделей микроуровня не представляется возможным в связи с крайне малыми размерами, поэтому целесообразно осуществлять экспериментальный контроль получаемых результатов конечно-элементного анализа привлекая модели субмакро- или макроуровней.

При моделировании топографических особенностей фрагмента шероховатой поверхности используется симплифицированный (например, при помощи цифровой фильтрации частот случайного сигнала) вектор поверхностной матрицы высот микронеровностей оригинального образца из латуни CuZn25 (рис. 2). Поверхность образца сканирована бесконтактным оптическим профилометром и восстановлена в цифровом виде стандартными программными средствами с дискретизацией до матрицы в 256x256 точек.

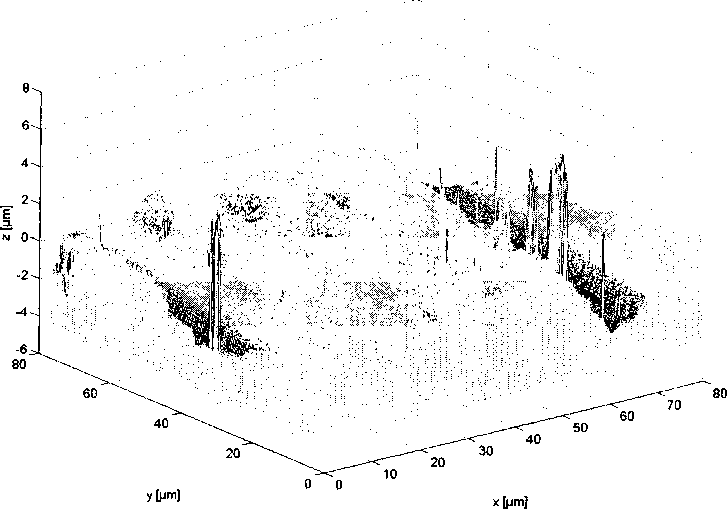
Рис. 2. Результаты сканирования и цифровой обработки поверхности латунного образца

При представлении оригинальной матрицы высот микронеровностей в виде совокупности векторов, формирующих матрицу поверхности, удовлетворительные результаты может дать способ параллельного переноса произвольного оригинального вектора (рис. 3). Однако полученная таким способом поверхность не обладает свойством общности для большинства инженерных поверхностей, поскольку представляет собой частный случай формирования поверхности механической обработкой (например, фрезерованием, плоским шлифованием или полированием) с явно выраженным направлением перемещения обрабатывающего инструмента.

Расчет и конструирование

Известна возможность создания математической модели шероховатой поверхности в виде совокупности отдельных формирующих векторов, причем каждый последующий вектор получают преобразованием предыдущего. В этом случае внешний вид полученной поверхности близок к внешнему виду реальных инженерных поверхностей, прошедших механическую обработку (например, плоским шлифованием), а топография поверхности удобна для создания конечноэлементной модели.

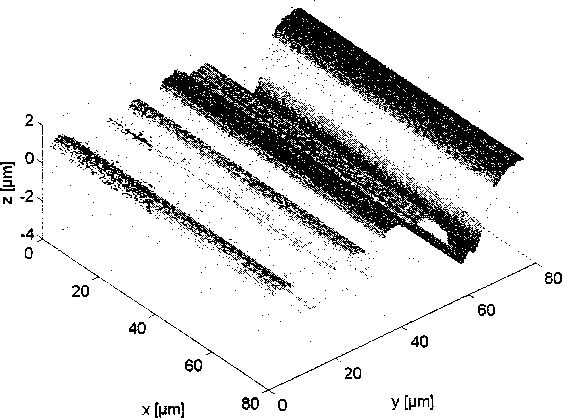
Рис. 3. Формирование рельефа фрагмента шероховатой поверхности параллельным переносом исходного профиля

Для реализации этого подхода в инженерной практике используют ортогональные преобразования, поскольку они позволяют осуществить преобразование оригинального вектора при полном сохранении его энергетической насыщенности, как эквивалента энергетических затрат, необходимых для разрушения формируемых данным вектором высот микронеровностей поверхности. Таким образом, эти преобразования представляют собой наглядный и эффективный инструмент генерации случайных сигналов с заданными энергетическими свойствами, которые могут быть использованы для создания конечно-элементных моделей контактных сопряжений.

Сущность метода ортогональных преобразований заключается в формировании модели контактной поверхности последовательным вращением оригинального произвольного вектора матрицы высот поверхности при полном сохранении его геометрических и, следовательно, энергетических характеристик, поскольку ортогональные преобразования позволяют изменить амплитуды вектора, но сохранить, суммарное значение функции спектральной плотности. Случайный сигнал, при этом, следует рассматривать в дискретном его представлении, как совокупность отсчетов в соответствии со степенью дискретизации.

Математически, ортогональные преобразования могут быть выполнены произведением оригинального вектора и ортогональной матрицы, т.е. матрицы, для которой сопряженная ей матрица равна обратной. Такое преобразование называют поворотом вектора, а ортогональную матрицу - матрицей вращения. Таким образом, для создания модели шероховатой поверхности в виде совокупности отдельных формирующих векторов, каждый последующий вектор получают поворотом предыдущего на некоторый угол ф.

Если в качестве оригинального вектора принят вектор случайного профиля матрицы поверхности, то суммарное значение функции его спектральной плотности должно быть определено как где: ^Р(®)5 - суммарное значение функции спектральной плотности вращаемого вектора;

^ Р^со)_м - суммарное значение функции спектральной плотности оригинальной матрицы;

N - количество векторов оригинальной матрицы.

Лазарев В.Е., Грамм М.И., Лазарев Е.А., Лаврик А.Н.         Математическая модель шероховатой

Franek F., Pauschitz A., Vorlaufer G., Jlsa R.поверхности контактного трибосопряжения

Оценка величин спектральной плотности оригинальной поверхности и поверхности, полученной при помощи ортогональных преобразований, может быть выполнена представлением моделированной матрицы высот поверхности в виде амплитудно-частотного спектра с определением суммарного значения функции спектральной плотности.

Для проведения ортогональных преобразований вектора высот исследуемой матрицы необходимо выполнить предварительную подготовку ортогональной матрицы вращения Т. Для этого можно использовать известную матрицу Гивенса:

cos ф -sin ф sinp cos#?

Использование модифицированной матрицы Гивенса удобно ввиду возможности задания угла поворота вектора в явном виде и моделирования поверхности с идентичным суммарным значением функции спектральной плотности (рис. 4).

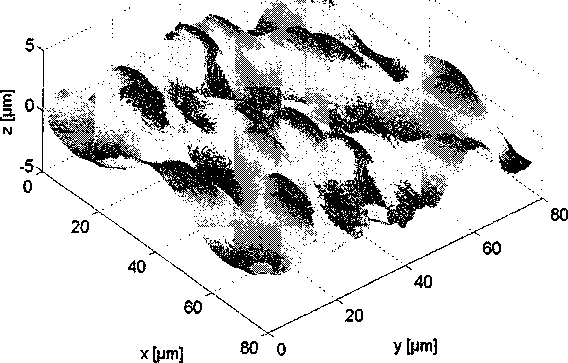
Рис. 4. Формирование рельефа фрагмента шероховатой поверхности поворотом исходного профиля и параллельным переносом

Ортогональная матрица для поворота вектора с числом элементов более двух может быть представлена аналогом матрицы Гивенса с заполненными диагоналями и всеми внедиагональными элементами, равными нулю.

Характерно, что при изменении формы получаемой поверхности ее спектральная плотность остается неизменной по отношению к спектральной плотности поверхности, полученной путем параллельного переноса исходного профиля без осуществления операции вращения.

При условии постоянства номинальной площади исследуемого образца и неизменной степени дискретизации - суммарное значение функции спектральной плотности, характеризующее уровень энергетических затрат на разрушение микронеровностей в контакте, может быть использовано, как оценочный критерий при фильтрации случайного сигнала с целью упрощения поверхностной топографии. В том случае, если разность суммарных значений функции спектральной плотности для матрицы поверхности до и после выполнения фильтрации несущественна или суммарные значения функции спектральной плотности для оригинальной матрицы поверхности и ее топографической модели близки, то можно предположить близкие значения энергетических затрат для механического разрушения оригинальных и моделированных микронеровностей [3].

Произведение оригинального вектора 2_ф (I, j) и ортогональной матрицы вращения Т представляет собой вектор 2_ф та_ф (i, j), внешне отличающийся от оригинального:

Z

Расчет и конструирование

но с неизменными энергетическими характеристиками, т. е. с величиной суммарного значения функции спектральной плотности оригинального вектора

Моделирование шероховатой поверхности субмакромодели сопряжения следует разбить на три этапа. Первый этап предполагает формирование векторов микромодели, при помощи последовательных ортогональных преобразований оригинального вектора микромодели шероховатой поверхности, полученного профилометрированием. Второй этап предусматривает формирование вектора субмакромодели последовательной стыковкой подготовленных и продольно перенесенных векторов. На третьем этапе осуществляются ортогональные преобразования суммарного вектора субмакромодели и формирование результирующей матрицы высот микронеровностей.

Для исключения появления регулярности рельефа получаемого сигнала целесообразно использовать метод ортогональных преобразований векторов с выбранными случайным образом углами поворота ф.

Создание результирующей матрицы субмакромодели осуществляется ортогональным преобразованием суммарного вектора субмакромодели с последующим его параллельным переносом по аналогии с формированием топографии матрицы шероховатой поверхности на микроуровне. Оценка уровней энергетической насыщенности оригинальной матрицы поверхности и матрицы модели, полученной при помощи ортогональных преобразований, может быть выполнена представлением дискретного сигнала в виде амплитудно-частотного спектра и определением его спектральной плотности Piaf, как функции амплитуд Л(о) микронеровностей от частоты: Р(о) = |Дю)|².

Равенство суммарных значений спектральной плотности оригинальной матрицы высот микронеровностей и ее модели свидетельствует об адекватности оригинала и модели. При этом предполагается равенство энергетических затрат, требующихся для разрушения микронеровностей рельефа оригинальной поверхности и ее модели в ходе процесса трения и изнашивания.

Выводы

• 1.    Ортогональные преобразования вектора случайного сигнала позволяют, сохраняя его суммарную спектральную плотность, создавать модели шероховатых поверхностей с заданными энергетическими характеристиками, методом параллельного переноса.

• 2.    Для последовательного и пропорционального наращивания энергетической насыщенности оригинального вектора субмакромодели в процессе фрагментарного моделирования возможно использование метода стыковки при продольном переносе симплифицированных и ортогонально преобразованных векторов микромодели.

• 3.    Адекватность модели шероховатой поверхности ее оригиналу, полученному при помощи профилометрирования, может быть подтверждена оценкой суммарного значения функции спектральной плотности модели и матрицы высот микронеровностей оригинальной поверхности.

Научная поддержка

Работа выполнена при поддержке международной ассоциации по обеспечению сотрудничества с учеными Содружества независимых государств - INTAS (Brussels, Belgium) в рамках программы Fellowship Grant for Young Scientists (Ref. Nr. 03-55-2135) совместно с Австрийским центром компетентности в трибологии - АС2Т Research GmbH (Wiener Neustadt, Austria).