Математическая модель системы профессионального образования федерального и регионального уровней

Выпускники системы профессионального образования (ПО) являются основным источником удовлетворения потребности в рабочей силе на рынке труда, и их численная прогнозная оценка служит основой для расчета баланса трудовых ресурсов на перспективный период.

Прогнозирование численности обучающихся студентов позволяет в перспективе оценить объем государственных затрат на финансирование образования, которое для образовательных учреждений (ОУ) высшего профессионального образования с 2011 года станет подушевым.

Для описания потоков распределения выпускников школ и учреждений профессионального образования по приемам в учреждения системы профессионального образования применяется модель, аналогичная модели переноса вещества. Потоки людей записываются в виде балансовых уравнений на основе закона сохранения их численности. Записанная таким образом модель обладает свойством аддитивности и позволяет с достаточной точностью описывать коллективное поведение поступающих.

Новизной предложенной модели, отличающей ее от предшествующих [1], [3], является учет следующих особенностей:

• •    детальное описание структуры приема в образовательные учреждения профессионального образования всех уровней;

• •    переходы учащихся с курса на курс.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Система балансовых уравнений, с учетом дискретного времени, представлена в разностном виде.

Математическая модель состоит из трех частей: моделирование объемов приемов в образовательные учреждения профессионального образования; моделирование численности выпускников; моделирование количества обучающихся студентов.

Первая часть математической модели – моделирование объемов приемов в учреждения про

фессионального образования – записывается в виде системы из пяти разностных уравнений, соответствующих приемам пяти уровней профессионального образования (начальное (НПО), среднее (СПО), высшее (ВПО) (бакалавр), высшее (специалист), высшее (магистр)):

N 9     9 N 11     11 N 9r 9r N       11r     11r N 99

Pi  = Ui ■ ki - + Ui  ■ ki - + Ui  ■ ki - + Ut  ■ kt  -  + Ui ■

S       9    9 S       11     11 S       9r    9r S       11r

Pi = U i ■ k. - + U, ■ k_t - + U_t ■ k. - + U,   ■ k_t - +

N   N _ S     N   Nr _ S

+ V.   ■ k. ~ + V. , ■ k. - i i                  i-1       i

+ ( V V + v i S ) ■ k SV - S

<

p ^Vs = k ' ■ ( U ,¹ ■ k , ¹-' + U ^{,11 r} ■ k i

11 r _ V

+ V N ■ k ” -V +

+ V Nr ■ k ” -V + V S ■ k ,S-V + VSr ■ P V = (1 - k ' ) ■ ( U ," ■ k,"- ^V + U ,^{1, r} + V Nr ■ k ,Nr-V + V S ■ k , -V + V Sr ■ k i

• k i

Sr-V + V - ^Vr k V-V )

p Vm = kb_m ■ v iVb

• ■ k"^r-V + V N ■ kN

-^Sr -V + V - 1 ■ kV-V )

V +

Здесь используются следующие обозначения: P^N – прием НПО, P^S – прием СПО, P^Vs – прием ВПО (специалисты), P^Vb – прием ВПО (бакалавры), P^Vm – прием ВПО (магистры), U ⁹ – численность выпускников 9-х классов, U ¹¹ – численность выпускников 11-х классов, U ^{9 r} – выпускники 9-х классов прошлых лет, поступающие в текущем году, U ^{11 r} – выпускники 11-х классов прошлых лет, поступающие в текущем году, V^N – выпуск НПО текущего года, V^S – выпуск СПО текущего года, V^Nr – выпуск НПО прошлого года, V^Sr – выпуск СПО прошлого года, V^V – выпуск ВПО текущего года.

Для обозначения модельного времени вводится индекс i , который изменяется от начальной i s = 1 до конечной i f = 19 границы интервала исследования с шагом один год. Календарное время (годы) измерения данных меняется по закону t(i) = i + 2001. Так, t(i s ) = 2002 и t(i f ) = 2020.

Нестационарные коэффициенты вида k _i ^X_Y характеризуют долю потока X, вливающегося в поток Y.

Вторая часть модели описывает динамику выпусков из ОУ ПО. Выпуски из учреждений СПО и ВПО определяются численностью студентов на старших курсах прошлого года. Соответствующие уравнения записываются следующим образом:

V S = QV^S ■ ( ktgS^ + ktgS 41 + ktgS 5-i + ktgS ⁶ -i )

V V = V Vs + v Vb + v Vm

- V V = QV Vs ■ ( ktgVs i-1 + kigVsL + ktgVs 6 - i + ktgVs] -1 ) ,         (2)

V V = QV Vb ■ ( ktgVb 4 + ktgVb ⁵ -i )

V Vm = Qv Vm ■ ktgVm i.

где V_i ^S – выпуск ОУ СПО; QV^S – коэффициент, характеризующий выпуск СПО; ktgS _i ^j – численность студентов СПО в год i на курсе j ; V _i ^V – выпуск ВПО в целом, V _i ^Vs – выпуск специалистов; V _i ^Vb – выпуск бакалавров; V _i ^Vm – выпуск магистров; QV^Vs , QV^Vb , QV^Vm – коэффициенты, характеризующие выпуск ВПО соответственно для специалистов, бакалавров и магистров; ktgVs _i ^j – численность специалистов ВПО в год i на курсе j ; ktgVs _i ^j – численность бакалавров ВПО в год i на курсе j ; ktgVm _i ² – численность магистров на 2-м курсе в год i .

Третью часть модели составляют уравнения (3–22), описывающие динамику численности студентов по курсам.

Уравнения для нахождения численности контингента студентов по курсам имеют следующий вид:

ktgVs} = qVsp1 ■ pVs ktgVsij = qVsj-1j ■ ktgVsi-1, j = 2..7 k-gib = qVb'' ■ PVb ktgVb/ = qVbj-1,j ■ ktgVb/--1, j = 2..5 ktgVmX = qVmp ■ pV ktgVm2 = qVm1,2 ■ ktgVm1—i ktgSl = cS ■ pS ktgSi2 = cS ■ PiS + qS1,2 ■ ktgSi—1

ktgSi* = c 3 ■ P ^S + qS ^2,3 ■ ktgSp

(4–9)

(11–14)

ktgS/ = qS j ^{- 1,}j ■ ktgS ip, j = 4..6 ,

(20–22)

где qVs^{p ,1}, qVb^{p ,1} – коэффициенты связи между

численностью студентов на первом курсе ( 1 ) и приемом ( p ) соответственно для специалистов и бакалавров; qVs j^{- 1,} j , qVb j^-1,j - коэффициенты перехода с курса j – 1 на курс j соответственно для специалистов и бакалавров ВПО (диапазон изменения j соответствует диапазону курсов обучения); c ₁ ^S , c ₂ ^S , c ₃ ^S – доля зачисленных соответственно на 1-й, 2-й и 3-й курсы в приеме СПО; qS j^{- 1,} j - коэффициент перехода с курса j - 1 на курс j для СПО.

Подход, использующийся для оценки численности студентов и выпуска учреждений СПО и ВПО, не применим для оценки численности студентов учреждений НПО, поскольку для учреждений, реализующих программы НПО, статистика распределения обучающихся по курсам

не представлена.

Данные о приеме НПО представлены в разрезе по продолжительности обучения поступающих (от 1 до 4 лет). Соотношения для расчета численности обучающихся и выпуска учреждений НПО в зависимости от приема записываются в следующем виде:

ktgNi = QktgN х х [Ni + N^ + Ni + N4 + Ni2-1 + N3-1 + N41 + N!3-2 + N4-2 + Ni-S ]

V N = QV N ■ ( N 1 - 1 + N 2-2 + N 3-3 + N 44 ) , ⁽²⁴⁾

где N _i ^k – численность поступивших в ОУ НПО в i -м году студентов по программам со сроком обучения k лет; QV^N , QktgN – коэффициенты пропорциональности, связывающие прием в учреждения НПО с выпуском и численностью студентов соответственно.

ОПИСАНИЕ ВНЕШНИХ ВОЗДЕЙСТВИЙ

В предложенной выше модели выпускники 9-х и 11-х классов школ являются фактором, осуществляющим внешнее воздействие на систему профессионального образования. Численность выпускников общеобразовательных школ напрямую влияет на объем приемов в образовательные учреждения профессионального образования. В свою очередь, численность выпускников школ напрямую зависит от демографического фактора рождаемости. Зависимость численности выпускников 9-х и 11-х классов от числа родившихся детей выявлена и описана в работе [2].

Численность выпускников 9-х классов школ определяется на основе демографического показателя рождаемости с помощью линейного уравнения:

U i ⁹ = 0,13 ■ X i _{- 14} + 0,75 ■ X i _{- 15}, (25) где U _i ⁹ – число выпускников 9-х классов, X i– 14 – число родившихся на 14 лет ранее; X i –15 – число родившихся на 15 лет ранее. Коэффициенты 0,13 и 0,75 определены при помощи регрессионного анализа.

Численность выпускников 11-х классов U _i ¹¹ определяется на основе численности выпускников 9-х классов двумя годами ранее с помощью линейного уравнения:

U ¹ = 0,65 -< 2 - (26)

Коэффициент, связывающий численность выпускников 9-х и 11-х классов, также определен при помощи регрессионного анализа.

Следуя таким соображениям, можно построить прогноз численности выпускников 9-х и 11-х классов до 2020 года на основе ежегодной численности родившихся детей до 2003 года.

ИДЕНТИФИКАЦИЯ ПАРАМЕТРОВ МОДЕЛИ

Математическая модель системы профессионального образования содержит 34 линейных конечно-разностных уравнения и 53 параметра (32 стационарных и 21 нестационарный).

Уравнения (3–5), (8–10) и (11–24), описываю- щие динамику приемов, выпусков и численности студентов ОУ ВПО, справедливы как для совместного, так и раздельного учета государственных и негосударственных учреждений ВПО.

При раздельном учете государственных и негосударственных вузов общее число уравнений модели возрастает до 54, число стационарных параметров – до 46, нестационарных – до 30.

К постоянным относятся параметры, характе- ризующие вероятность переходов студентов с курса на курс и выпуска студентов со старших курсов. Эти параметры достаточно надежно идентифицируются в виде средних на обучающей выборке ретроспективных данных, описывающих численность студентов по курсам и годам.

К нестационарным относятся параметры, ха- рактеризующие распределение выпускников школ и учреждений профессионального образования по приемам в учреждения профессионального образования, поскольку подчиняются явным тенденциям к изменениям, вызванным объективной социально-экономической ситуацией. Для идентификации таких параметров использовалась ап-

проксимация с помощью логистической кривой вида f (t) =

c

1 + b - e - a ' t

с учетом ограничения на чис- ленность выпускников. Например, для выпуск- ников 11-х классов:

k11_ V + k11_ S + k11_ N <  1,        (27)

где k 11_ V , k 11_ S и k 11_ N – соответственно доли выпускников 11-х классов, поступающих в ОУ ВПО, СПО и НПО. Средние относительные ошибки в процентах соответственно равны 3,1, 1,9 и 4,5 %.

ПРОВЕРКА АДЕКВАТНОСТИ МОДЕЛИ

Для проверки адекватности модели был проведен пост-прогноз с целью сравнения модельных и фактических данных.

При этом вся выборка имеющихся данных с 2002 по 2009 год была разбита на две – обучающую выборку (с 2002 по 2007 год) и контрольную (с 2007 по 2009 год). Далее проверялось соответствие фактических данных на период с 2007 по 2009 год с расчетными значениями для этого же периода. Пригодность модели для прогнозирования определялась на основании следующих числовых оценок: средние относительные ошибки в процентах (СООП) и О-критерия.

В таблице приведены величины и средние относительные отклонения в процентах для этих величин между фактическими и расчетными данными. Средние относительные ошибки не превышают 9 %, а O-критерий превосходит 0,9 для всех прогнозируемых величин, что свидетельствует о пригодности приведенной модели.

РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ ДО 2020 ГОДА

На рис. 1–3 приведены фактические данные с 2002 по 2009 год и результаты прогнозирова-

Результаты расчетов средних относительных ошибок и О-критерия для прогнозируемых величин

Величина	СООП	О-критерий
Прием ВПО	4,57 %	0,971
Прием СПО	3,79 %	0,965
Прием НПО	6,15 %	0,949
Выпуск ВПО	2,54 %	0,984
Выпуск СПО	1,91 %	0,989
Выпуск НПО	3,61 %	0,972
Численность студентов ОУ ВПО	2,08 %	0,987
Численность студентов ОУ СПО	1,29 %	0,992
Численность студентов ОУ НПО	8,89 %	0,941

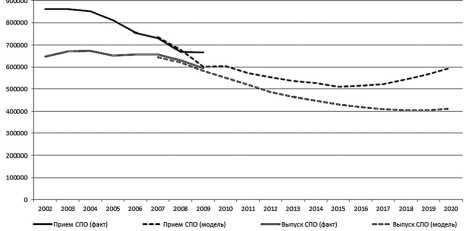
Рис. 2. Результаты расчета приема и выпуска из ОУ СПО

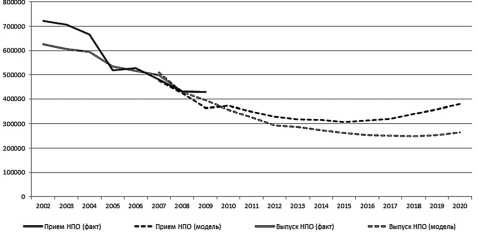
Рис. 1. Результаты расчета приема и выпуска из ОУ НПО

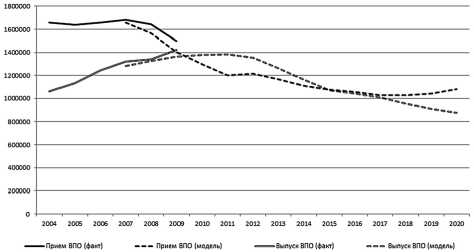
Рис. 3. Результаты расчета приема и выпуска из ОУ ВПО

ния приемов и выпусков до 2020 года для трех уровней профессионального образования по РФ.

АДАПТАЦИЯ МОДЕЛИ ДЛЯ РАСЧЕТОВ НА РЕГИОНАЛЬНОМ УРОВНЕ

Разработанная математическая модель позволяет прогнозировать распределение выпускников 9-х и 11-х классов школ по приемам в учреждения системы профессионального образования на уровне РФ. При этом учитывается, что эффект межрегиональной миграции, связанной с получением образования, на федеральном уровне не сказывается (сумма выбывших на учебу по всем регионам равна сумме прибывших в связи с учебой). Для расчетов на региональном уровне необходимо учитывать миграционные потоки граждан, меняющих место жительства в связи с учебой.

Ниже приводится описание разработанного алгоритма учета миграционных притоков и оттоков выпускников школ 9-х и 11-х классов, связанных с переездом в другие регионы для получения профессионального образования.

Исходные данные по миграции в связи с образованием берутся из форм статистической отчетности «МО-3» и «МР-1» [4], [5], [6], [7], [8], [9], [10], [11], [12], [13].

Обозначим число выпускников 9-х и 11-х классов, выбывших на учебу в другие регионы из m-го, соответственно U ° m t (f) и иЦ (i)(m e 1.J , J = 83 — по числу субъектов РФ). ^m

Число выпускников, продолжающих обучение в своем m-м регионе, будет равно U 9 m (i) - U o m (i) для выпускников 9-х классов и U₁₁ (i) - uH (i) -для выпускников 11-х классов. ^mm

Сформируем два вектора из m компонентов ( m e 1..J , J = 83) для выпускников 9-х и 11-х классов, каждый элемент которых характеризует долю оставшихся в m-м регионе выпускников:

Матрица Z 9 содержит в себе распределение в долях выпускников 9-х классов для каждого региона по регионам, в которых эти выпускники продолжают свое обучение. Диагональные элементы равны доле выпускников, оставшихся в своем регионе. Сумма по строке равна единице.

Аналогично создадим матрицу для выпускников 11-х классов:

Z11 = {Z11 kn }, k , n e 1..J , где
Z 11k ,n ='	K U 11k ’ k = n Mk , n    U°1T k
	83         TT U 11 ^ k-k ,n
	j = 1

, k * n

Введем так назыв _* аем _* ые приведенные локальные переменные: U _m ⁹ , U ¹ _m ¹ , которые будем определять следующими равенствами:

* 83

Um,i  ^ Z9k ,m " Uk,i , k =1

*     83

^Um,z = ^ ^{Z 11} k , m " ^U k , i .

k = 1

Эти переменные описывают вклад в приемах m -го региона выпускников 9-х и 11-х классов всех субъектов Федерации (в том числе и своего собственного).

Аналогичные выражения для выпускников 9-х и 11-х классов прошлых лет:

*        83

^{K U} s 9 m ⁼

U (i) - UO“ (i) 9 m        9 m

U (i) 9m x 7

^Umi ^-1 ^ Z ⁹ k , m "  ^Uki ^-1 , k = 1

*       83

U L¹, - 1 = S Z 11 _km " U^ ¹ - 1 . k = 1       ’

– для выпускников 9-х классов и

_KU s _{11 m}

U_n (i) - UT (i) ¹¹m _____ ¹¹ m

Uli (i)

iim x /

– для выпускников 11-х классов. Сумма элементов этих векторов равна единице.

Пусть существует квадратная матрица м = { M k n } размером 83 х 83 (по числу субъектов Федерации), элементы которой представляют собой численность мигрантов, убывших из региона k в регион n с целью получения образовательных услуг. Диагональные элементы этой матрицы – нули.

Создадим матрицу Z₉ = {Z₉ k n }, k , n e 1.. J , J = 83,

Таким образом, с учетом всех прибывших на учебу в m -й регион выпускников 9-х и 11-х классов, как текущего, так и предыдущего года, из всех других субъектов Федерации, для m -го cубъекта система уравнений (1), описывающая приемы по всем уровням профессионального образования, записывается следующим образом:

p N.= p.-l-NN

1 m,i   mml ^m,i

P S ■ - U⁹ ■ m,l m_mj

+ U '<.ku-N m,i

*U’■ ,-k9rN+ t/1f       -N+ U9 -k’w m,i-1 m,i          m,i-1 m,i           m,i m,i

■k’-S+          S m,i        m,i m,i

WN-kN - ⁺ m,l тщ,1

’* j-’r Sj- Z-11r St

^{+ U} m,i - 1 "  ^k m,P  ^{+ U} m,i - 1 "  ^k m ,C  ⁺

+ vN .-kN-S+(VV +PS vk^SV -S ⁺ 'm,i - 1 ⁿ’m,i     ⁺ v m,i ⁺ 'm,i ) тщ,!

где

Z

⁹ k , n

K U 9 k , ^k = n

⎪             out

J M k , n ^U9_k_ , k * n 83 П

У M.  ^U9k

^ k-K,n

. j = 1

VVs ^Vs /гг1Г ,11 V , г,1Г , 11r V , nN I N V , ^Pm,i = ^k m,i "  ^{( U} m,i "  ^km,T ^{+ U}m,i-1 "  ^k m,i ” ^{+ V} m,i "  ^km,F ⁺

WNr-k^r-^V₊ yS.._kS-^V₊y^r-k^r-^V₊ V^V. _vk^V -V) +' m,i  ^m,!    ⁺   m,i ⁿ'm,i    ⁺   m,i  ⁿ'm,i     ⁺   m,i-1  mn,i  )

v Vb   _Z1   , Vs x z_T, 1Г , 11  V , _T, 1Г    , 11r  V , nN i N V ,

^Pm,i   ^{(1   k} m,i ) "  ^{( U} m,i "  ^k m,i ^{+ U} m,i - 1 "  ^k m,i ^{+ V}m,i "  ^k m,i ⁺

WNr-kNr-V + VS .-k ^S-^V + PSr .kSr-^V+P^V , ._k^V-^V) +' m,i ^m,i ⁺ m,i ⁿ'm,i ⁺ m,i ⁿ'm,i ⁺ 'm,i - 1 ⁿ'm,i )

V Vm₌kb , m ,_rVb m,i               'm,/

Такой учет миграционных образовательных потоков позволяет адаптировать федеральную

модель распределения выпускников по приемам в образовательные учреждения профессионального образования к расчетам на региональном уровне.

ЗАКЛЮЧЕНИЕ

В статье приводится описание математической модели, позволяющей на основании прогноза численности выпускников 9-х и 11-х классов школ и данных о текущей численности студентов по курсам строить прогнозы приемов и выпусков учреждений профессионального образования.

Математическая модель представлена в виде системы из 34 линейных разностных уравнений, содержащей 32 стационарных и 21 нестационарный параметр. Записанная в таком виде модель позволяет прогнозировать прием, выпуск и чис- ленность студентов ОУ НПО, СПО и ВПО с относительной ошибкой, не превышающей 10 %. Кроме того, для системы ВПО модель позволяет оценивать прием, численность и выпуск студентов для бакалавров, специалистов и магистров как для государственных, так и для негосударственных высших учебных заведений. Приводятся результаты количественного прогнозирования численности приемов и выпусков в учреждениях профессионального образования всех трех уровней до 2020 года для РФ.

Показано, что при учете межрегиональной миграции, связанной с образованием, данная модель позволяет проводить расчеты численности приема, выпуска и количества обучающихся студентов не только на уровне России в целом, но и на уровне субъектов РФ.