Математическая модель течения двух вязкопластичных сред в формующем канале экструдера при коэкструзии

Композиционное совмещение в одном продукте растительных и животных составляющих с заданной рецептурой может быть достигнуто с помощью коэкструзии, использование которой позволит значительно расширить ассортимент и номенклатуру выпускаемых поликомпонентных продуктов, сбалансированных по химическому составу и с программируемыми свойствами. При их производстве внутренний слой формируется из жи-ровитаминной начинки, а внешняя оболочка – из экструдата, полученного на основе зерновых [1].

Процесс коэкструзии в каналах формующей головки будет стабильным, если при давлении, достаточном для распределения материала, время пребывания в нем экструдата будет минимальным [2]. Решение данной задачи требует точного описания течения материалов в формующем канале.

Рассмотрим цилиндрическую формующую головку (рис . 1), в которую подаются две неньютоновские среды с различными реологическими законами без взаимного перемешивания.

Протекание изучаемого процесса зависит от соблюдения абсолютного равенства условий в подводящем патрубке и предматричной зоне.

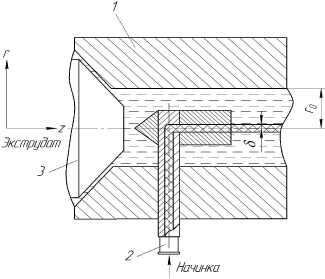
Рис. 1. Расчетная схема течения экструдата и начинки в формующем канале экструдера: 1 – корпус формующей головки; 2 – подводящий патрубок; 3 – предматричная зона

В изотермических средах векторная запись уравнений неразрывности и движения примет вид [5]:

Dp -p^) ^, (1)

P D = "^v P + [ V- r ] + p- g ,

где D – полный дифференциал; t – теку щ ее время; ρ – плотность среды; ∇ – градиент; ν – вектор скорости движения среды; ∇ Р – градиент давления; τ – касательное напряжение; g – вектор ускорения силы тяжести.

Принимая, что среда несжимаема ( ρ = const) и сила тяжести пренебрежимо мала по сравнению с действующим градиентом давления, запишем уравнения (1) и (2) в цилиндрической системе координат с учетом симметричности оси в компонентной форме:

1 ∂

r ∂r

f г П ⁰

V

∂ ν z	n - 1 dv z	= ∂ ρ
∂ r	д г	д z

Так как при этом в канале выполняется условие ( dv z /d r ) ) 0, то

no A / dvz)n =dp

г дг V d г )     dz

1 ∂         ∂ τ

( r ⋅ τ r ) +    ^z = 0,

r ∂r ∂z

f dv dv)

P l Г ' -V I =

V   d r      d z у

= ^{∂ ρ} + 1 ^∂ ( r ⋅ τ ) + ^∂ r^rz , ∂ r r ∂ r ^rr ∂ z

f dv dv)Pl Г ' + V I =

V   d r       д z у

= -    +      ( r ⋅ τ _rz ) +      ,

∂z   r ∂r          ∂z

где r, z – локальные цилиндрические координаты; ν r , ν z – координаты вектора скорости ν ; τ _rz, τ _zz, τ _rr - компоненты тензора напряжений τ .

Учитывая высокую вязкость сред, концевыми эффектами (начальный гидродинамический участок и выходное сечение формующего канала) можно пренебречь, тогда течение будет однонаправленным, то есть компоненты скорости будут зависеть только от цилиндрической координаты r . В этом случае система (3)-(5) упрощается:

1 ^∂ ( r ⋅ τ ) = ^{∂ ρ} , r ∂ r     ^rz    ∂ z

а компонента тензора напряжения τ _rz, в соответствии с законом Оствальда-де-Виля примет вид

τ _rz = η ( ∂ ν _z ∂ r ) , в котором динамическая вязкость:

η=ηo

∂ ν _z ∂ r

n - 1

,

где η ^o – вязкость среды при скорости сдвига, равной 1 с^-1, n – индекс течения, соответствующий при 0 <  n < 1 вязкопластической среде, а при n > 1 – дилатантной.

Таким образом, на основании (6)-(8)

можно выразить однонаправленное движение неньютоновской среды:

При течении экструдата и начинки в формующем канале экструдера уравнение (9) справедливо, поэтому течение двух несмеши-вающихся вязкопластичных сред в цилиндрическом канале описывается системой

η ₁ ∂ r ∂ r

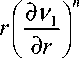
η 2 ^∂ r ∂ r

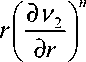
где η 1 , η 2 – вязкость экструдата и начинки при скорости сдвига, равной 1 с^-1; n 1 , n 2 – индекс течения экструдата и начинки; ν ₁, ν ₂ – скорость экструдата и начинки, м/с.

Система (10) и (11) замыкается граничными условиями "прилипания" на корпусе формующего канала равенства скоростей течения экструдата и начинки на границе их раздела

ν ₁ ( δ ) = ν ₂ ( δ )

и касательных напряжений

η 1

∂ ν 1 ( δ ) ∂ e

n ₁

= η 2

∂ ν 2 ( δ ) ∂ r

n ₂

,

а также условием симметричности оси

∂ ν ₂ ( 0 ) ∂ r_o

где r o , δ – радиусы подводящего формующего канала, м.

Решая дифференциальные

(10) и (11), получаем:

ν 1 ( r ) =

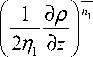
1 + n ₁ r_o n 1

патрубка и уравнения

n ₁

n ₁ + 1

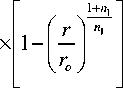
^V 2 ( Г ) =

" n 2

" 2 + 1

1+"-)1

V ro ) V ro)

1 + n 1

r On¹

1 + " 2

r On⁷

1 + n ₁

при рассмотрении не только дилатантных сред, но и смешанных. Вязкопластическое течение проявляет характерную черту вязких жидкостей, особенно у стенки канала. Физический смысл параметра K идентичен градиенту давления (рис. 2). Чем больше перепад давления в канале, тем выше скорость течения среды у его оси, причем характеристики пристенного течения остаются постоянными. Варьирование индекса течения у жидкости, текущей

у стенки, сильно влияет на расходные характе-

В относительном виде (12) и (13) запишем при условии А <  R <  1

1 + П 1

при 0 <  R <  1

1 + n 1         f 1 + и ₂       1 + и ₂ Л

где

^ R )=---

" 1

" 1 ^- "  2

П \' | r_o d P । " 1 " 2 _

Л^П 2 ²

/

—

1                  ¹⁺ " 1

;

" 1 + 1 V 2 ^ 1 d z ₎

o

ристики.

Анализ вычислительных экспериментов показал, что при дозировании сред в формующем канале, если задано соотношение объемных расходов экструдата и начинки, необходимо определять гидравлический диаметр дозирующего патрубка.

Так, если

Q1М = Y, где roэ-1

Q 1 = 2п J rv_x dr = 2 n r_o² V J RV 1 ( R ) dR

5А

и

5_А

Q2 = 2nJrv2dr = 2nro2vJRV2 (R)dR , то радиус дозирующего канала (относительно А) определяем из трансцендентного уравне

ния:

V 2 ( ^R ) =

—

" 1

1 d p " 1

1 + n 1

^^^^Ш

" 1

1 + 3 " j

n 1 + 1 V 2 % d z _y

r o" ¹

_f        1 + 3 " [ Л

R = r[r_o и А = 5 r_o .

Вычислительный эксперимент прово-

)

--"^- K А ""

1 + 3 " ₂

^ .(14)

дили для случая, когда экструдат и начинка -вязкопластические среды, то есть 0 <  n 1 ,

n ₂< 1. Заметим, что нет никаких затруднений

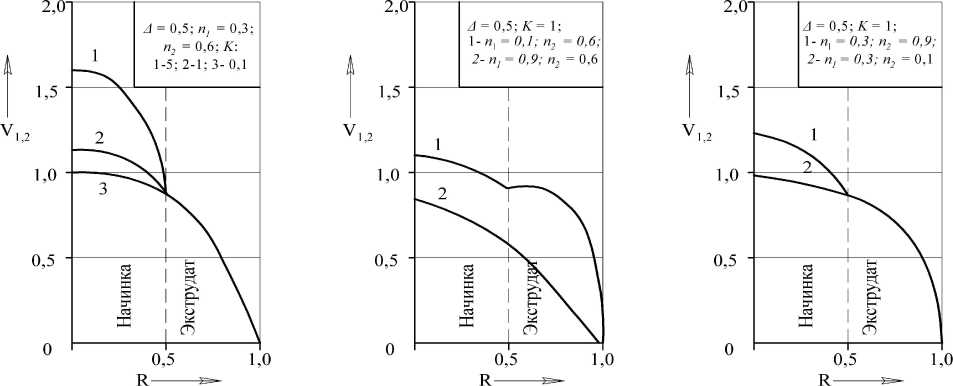
Рис. 2. Профили скоростей при различных значениях K ; n 1 и n ₂

Пример расчета. Определим диаметр дозирующего патрубка при получении полнорационного комбикорма с начинкой методом коэкструзии. Реологические характеристики зерновой смеси и жировой начинки в соответствии с [3] таковы: η 1 = 11724 Па ⋅ сⁿ, n 1 = 0,549; η 2 = 196 Па ⋅ с, n 2 = 1 радиус формующего канала экструдера r o = 3,5 ⋅ 10^-3 м, длина Δ Z = 9,87 ⋅ 10^-3 м, давление в предматричной зоне P 1 = 7 МПа, атмосферное давление P 2 = 0,1 МПа, сбалансированное соотношение зерновой составляющей и жировой начинки 2:1 [5], то есть γ = 2.

Градиент давления в формующем канале ^{∂ ρ} ≈⁽ P ^{1 -} P ^{2 )} = 7,8 ⋅ 10⁸ Па/м, K = 0,593. ∂ z     ∆ z

В результате решения трансцендентного уравнения (14) методом бисекции [4] находим Δ = 0,1091, δ = 3,8 ⋅ 10^-4 м. Если при определении объемных расходов компонентов комбикорма исходить из соотношения площадей проходных сечений течения экструдата и начинки, то радиус дозирующего канала равен δ = 2 ⋅ 10^-3 м. Таким образом, ошибка в рецептуре комбикорма в этом случае может достигать существенных значений.