Математическая модель тепловлагопереноса в мерзлой почве

Почвенная влага – ресурс для развития растений и один из основных факторов, определяющих условия обработки почвы.

Генетико-гидрологическое направление изучения водного режима почвы связано с разработкой агротехнических приемов повышения влагообеспеченности сельскохозяйственных культур.

Почвенная влага отличается от воды рядом особенностей. Она размещена в пористой, высокодисперсной и анизотропичной почвенной среде. В состав почвы входят как мельчайшие частицы коллоидальной и молекулярной дисперсности (диаметр – 10–6–10–3 мм), так и частицы грубой дисперсности (диаметр – более 1 мм). Почвенная влага находится под воздействием сил, зависящих от размеров и формы почвенных пор, а также от природы почвенных частиц.

Движение воды в почве может осуществляться путем диффузии – передачи движения от молекулы к молекуле, при котором радиус действия сил, вызывающих движение, соизмерим с размерами молекул, а величина молекул соизмерима с силами молекулярного сцепления, или путем движения массы молекул воды как единого целого под влиянием менисковых сил и сил тяжести.

В природных условиях в почве содержится некоторое количество влаги, которое может находиться в жидком, твердом (лед) и парообразном виде. Вследствие постоянного обмена между почвой, атмосферой и растением содержание влаги в почве непрерывно изменяется.

Почва, когда часть пор свободна от воды, представляет трехфазную систему почва – вода – воздух. Закономерности равновесия и переноса почвенной влаги в таком случае значительно усложняются.

В настоящее время существует два подхода к оценке и характеристике процесса передвижения влаги в почве: 1) выявление конкретных механизмов движения влаги в почве и их роли на основе сущности явлений и причины связей, а также с помощью учета сил различной природы, определяющих движение; 2) установление общих закономерностей, равновесие и направление движения воды в почве, отвлекаясь от конкретных механизмов ее переноса – термодинамический подход, при котором силы различной природы, в совокупности определяющие поведение воды в почве, объединены в одну равнодействующую.

Если механизмы передвижения влаги в незамерзших почвах изучены достаточно, то ее фильтрационные закономерности в мерзлых почвах требуют дополнительных исследований.

Накопление влаги твердых осадков, доля которых в формировании урожая в засушливых регионах достигает до 50%, в период таяния снега, в условиях промерзшей и оттаивающей почвы – важнейшая задача для зон рискованного земледелия.

Теоретические исследования, направленные на получение знаний, позволяющих осуществить адаптацию рабочих органов машин с воздействием на почву к агротехническим приемам основной обработки по накоплению и использованию вневегетацион-ной части атмосферных осадков, и отвечающие на вопрос: пропускает ли воду мерзлая почва – актуальны.

Цель исследований – математизация термодинамического подхода к оценке состояния и передвижения талых вод в замершие почвы.

Объект и методы исследований

Объект исследований – процесс инфильтрации талых вод в замершие почвы.

Предмет исследований – закономерности условий передвижения почвенной влаги.

Методы исследований включают функциональный анализ и моделирование, натурный эксперимент.

Результаты теоретических исследований

Математическая модель тепловлагопереноса в почве весной

Почвогрунты согласно современным представлениям о их структуре связей представляют трехкомпонентную систему, включающую твердую, жидкую и газообразную составляющие. Степень дисперсности почвогрунтов определяется размерами почвенных частиц, промежутки между которыми (поры) могут быть заняты одним воздухом, если почва абсолютно сухая. Однако чаще всего поры между твердыми частицами заполнены не только воздухом, но и однокомпонентной трехфазной системой – лед – вода – пар.

В почвах со значительным содержанием илистых и коллоидных частиц диаметром меньше 0,001 мм могут преобладать микропоры диаметром 10–4–10–5 мм. Вода в таких порах практически неподвижна, почти полностью связана поверхностными силами.

В почвах, основу которых составляют микроагрегаты диаметром 0,05–0,25 мм, различают два типа пор: внутри микроагрегатов диаметром 10–4–10–5 мм – капиллярные и между агрегатами диаметром 10–2–10–3 мм – некапиллярные, вода в таких порах подвержена гравитационной силе тяжести и способна перемещаться вглубь почвы, т.е. фильтроваться. Таким образом, водопроницаемость почвогрунта в значительной степени зависит от пористости и диаметра пор. В дальнейшем водопроницаемость будет ха- рактеризовать коэффициент водопроницаемости, изменяющийся в зависимости от глубины и состояния почвы.

Эмпирическая зависимость коэффициента водопроницаемости k от некапиллярной пористости p (x) и диаметра пор d приведена в табл. 1 [1–4].

Таблица 1

Зависимость коэффициента водопроницаемости от пористости и диаметра пор

Пористость, %	Диаметр пор, мм
	1,0	0,5	0,3	0,1	0,05	0,01
30	0,2	0,050	0,018	0,002	0,00050	0,00002
35	0,3	0,075	0,027	0,003	0,00075	0,00003
40	0,5	0,135	0,045	0,005	0,00125	0,00005
45	0,7	0,175	0,063	0,007	0,00175	0,00007
50	0,9	0,225	0,061	0,009	0,00225	0,00009

Из данных табл. 1 видно, что коэффициент водопроницаемости пропорционален величине d2, что согласуется с эмпирическим законом Дарси [5], согласно которому скорость фильтрации в пористых средах связана с градиентом давления по закону

;

Sir)

SR2

, где s – площадь поверхности фильтрации, мм2; p – вязкость воды, г/мм∙сек; : – высота фильтра, мм; Др – перепад давлений, г/мм2; и – скорость фильтрации, мм/с; К – коэффициент водопроницаемости; R – радиус пор, мм.

В дальнейшем для более тонкого понимания процессов, происходящих в почве при тепловлагопереносе, удобно разделять капиллярную и некапиллярную пористость, а под пористостью почвы понимать полную пористость.

Рассчитана полная пористость может быть по формуле

Р=1-Р/ =^. / d d;

где Р – пористость почвы, %; ρ – плотность, г/см³; d – удельная масса, г/см³.

Удельный вес большинства почв – 2,5–2,7 г/см3 [1–4]. Плотность почв пахотного слоя колеблется в пределах 0,9–1,6 г/см3, причем у глинистых черноземов плотность – 0,9 г/см3. Зависимость пористости почвы от ее плотности при d = 2,6 г/см3 приведена в табл. 2.

Таблица 2

Зависимость пористости почвы от ее плотности (для значения d = 2,6 г/см3)

Плотность, г/см3	0,9	1,0	1,1	1,2	1,3	1,4	1,5	1,6
Пористость	1,6	0,62	0,58	0,54	0,50	0,46	0,46	0,38

Распределение пористости на капиллярную и некапиллярную в зависимости от диаметра микроагрегатов представлено в табл. 3.

Таблица 3

Зависимость капиллярной и некапиллярной пористости от диаметра микроагрегатов

Пористость, %	Диаметр микроагрегатов, мм
	0,5	0,5–1	1–2	2–3	3–5
Полная	47,5	50,0	54,7	59,6	62,6
Капиллярная	44,6	25,5	25,1	24,5	23,9
Некапиллярная	2,7	24,5	29,6	35,1	38,7

С пористостью тесно связано такое важное понятие, как влажность почвы. Очевидно, что полная влажность не превосходит полную пористость.

Поскольку за основу деления пористости на капиллярную и некапиллярную принята способность почвы к фильтрации влаги, то, естественно, полную влажность следует разделять на капиллярную и некапиллярную. При этом способностью к фильтрации обладает только вода поверхностного слоя почвы (некапиллярная влажность).

При весеннем тепловлагопереносе почва находится в отрицательном температурном интервале. Следовательно, наряду с процессом смачивания (повышение капиллярной влажности) при фильтрации воды в почве протекают процессы теплообмена, следствие которых – переход почвенной влаги из жидкого состояния в твердое и обратно.

Поскольку при изменении капиллярной влажности в почве перемещения влаги происходят на расстояния 10^–2–10^–3мм, можно пренебречь временем капиллярного насыщения и считать, что капиллярная влажность достигает максимального значения, равного капиллярной пористости S k (x), в момент достижения соответствующей глубины x капиллярной влагой. В дальнейшем капиллярные поры и капиллярная влага не оказывают влияния на скорость фильтрации некапиллярной влаги. Кроме того, будем считать, что скорость фильтрации влаги в некапиллярных порах подчиняется закону Дарси (формула (1).

Примем также, что теплообмен воды с почвой при ее фильтрации вглубь происходит по схеме:

– капиллярная, т.е. неподвижная, влага обменивается теплом с почвой и некапиллярной, подвижной влагой;

– некапиллярная влага обменивается теплом только с капиллярной влагой;

– замерзанию подвержена только капиллярная влага (т.е. количества теплоты, выделенной при замерзании капиллярной влаги, достаточно для разогрева почвы до 0°C).

Приведенная ниже математическая модель представляет основу описания процессов тепловлагопереноса в почве. В модели не учтены влияние теплового потока и вла-гопереноса из глубины почвогрунта и его неоднородности.

Также отметим, что данная модель ориентирована на описание относительно быстропротекающих процессов тепловлагопереноса с поверхности почвы, происходящих в период весеннего снеготаяния, и не учитывает более медленные процессы [6].

В соответствии с вышеизложенным математическая модель процессов фильтрации воды и теплообмена в весенний период должна строиться с учетом соотношений:

;

v(x,t)SHK(x)=SHK(0)o(0,t),(5)

при 0 ;

V^^5^^ [pg-gradPMj;(6)

при 0 ;

^ = д(с)-5ю(0)ч,(0,е);(7)

ShkM ■ ^CB p^ (^x-0 + 4^X, 0 ^7 I^х» O] =

• = ^ [kB(x)^ " ^нк(х'О] ~ а5Д£(х)[7^(х, t)~TK{x, t)],(8)

при            ;               ;.

SrVx) "  C_B -^ (x, t) = aS_K (х)[7^_д(х, t) — T_K (x, t)] +

+/?5K(x)[Tn(x,t) - Гд(хЛ)],(9)

при S’3-"-- : ; - - и .. ." .2. ; . ;■:.: 2; ...:.." < /;

-             7 = 2 7      7      7      7 ;, при sYc ." ; Гу : 2; Г. :. : -Г;

при Г_кл;д.>0 ; Г_я&дМ1;

,

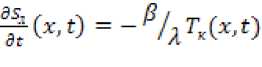
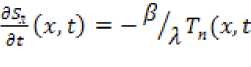
, при ; ?.;.:= .';

где J.. .г - капиллярная пористость почвы, %; 7.... .=• - некапиллярная пористость почвы, %; 7 л - полная пористость почвы, %; 7. л - доля льда в почве; ". т : - скорость фильтрации некапиллярной влаги, мм/с; 7:' /) - высота слоя воды над почвой, мм; - : -низкий уровень насыщения некапиллярной влагой, мм; 7 v " - давление воды в некапиллярных порах, г/мм2; 7.. :v : - температура капиллярной влаги, :С; 7.... * : - температура некапиллярной влаги, :С; 7. т : - температура почвы, :С; ч.. - теплопровод- ность почвы 2.-222  2 22 2 2 ч;?л ::: :;  -:

теплопроводность льда,

–

2 2 2 2 22 22"7;?.л ::: :; ч_. - теплопроводность воды 2 25 2 - 2 5:2  2:2 ^"Ухл ::: :;

• 2.. - теплоемкость воды, 1 кал/см³ • град; 2.. - теплоемкость почвы, 0,2 кал/см³ • град; •• - - вязкость воды, 0,1797 • 10^-2(1 + 0,0337 • Т + 0,000221 • 1²)^-1 г/см^с; ." - коэффициент теплообмена между капиллярной и некапиллярной водой, кал/см³^страд; а - коэффициент теплообмена между капиллярной водой и почвой, кал/см³^страд; .; : - при

ток талой воды, мм.

Для того чтобы соотношения (4)–(12) корректно описывали процессы тепловла-гообмена в почве, их необходимо дополнить граничными и начальными условиями:

S^C^O) = О, Г„(х,0) = G(x), h(x,O) = О, 7.. v 2 =2, 7... 2 : = 2-2^:7 , z(0) = 0. ,                                                               .

Кроме того, необходимо задать приток талой воды. В качестве притока g (t) выберем кусочно-линейную функцию, ее значения в узлах представлены в табл. 4.

Показатели плотности почвы, пористостей, радиуса пор, содержания влаги в почве выбирались на основе табл. 1-3 и приведены при описании результатов численных расчетов.

Уравнения (4) и (5) определяют условие сохранения количества влаги в почве с учетом ее перехода в некапиллярную и капиллярную.

Уравнения (6) представляют эмпирическую закономерность, основанную на соотношении (1).

В уравнениях описаны:

Уравнение (7) - изменение уровня надпочвенных вод с учетом притока снеговой воды.

Уравнение (8) - процесс изменения температуры в некапиллярной почвенной влаге с учетом ее перемещения в результате фильтрации, внутренней диффузии и теплообмена с капиллярной влагой.

Таблица 4

Распределение притока талой воды g (t), мм/час, в зависимости от суток таяния и времени суток

Сутки	Время суток, час
	6–11	11–12	12–13	13–14	14–15	15–16	16–17	17–18	18–24
1-е	–	–	0,25	1,25	4,0	3,5	1,0	–	–
2-е	–	0,1	0,40	1,40	7,5	7,0	7,2	0,4	–
3-е	–	0,2	0,80	1,90	12,1	11,5	7,5	1,0	–
4-е	–	0,3	1,20	2,50	18,0	16,0	10,0	2,0	–
5-е	–	0,5	1,50	3,00	23,0	21,0	16,0	3,0	–
6-е	–	0,8	2,00	3,70	30,0	28,0	15,5	4,0	–
7-е	0,15	1,25	2,50	4,35	36,0	34,0	19,0	6,0	0,15
8-е	20,00	20,0	40,0	75,0	90,0	40,0	35,0	15,0	20,0
9-е	90,00	50,0	70,0	190,0	250,0	240,0	140,0	50,0	100,0
10-е	60,00	70,0	150,0	200,0	310,0	300,0	170,0	80,0	70,0
11-е	45,00	60,0	100,0	110,0	170,0	180,0	70,0	20,0	50,0
12-е	30,00	20,0	50,0	40,0	110,0	120,0	40,0	10,0	40,0
13-е	–	5,0	25,0	30,0	50,0	55,0	15,0	–	–

Уравнение (9) – процесс изменения температуры в капиллярной почвенной влаге с учетом теплообмена с некапиллярной влагой и почвой.

Уравнение (10) – процесс изменения температуры в почве с учетом теплообмена с капиллярной почвенной влагой.

Уравнения (11) и (12) – фазовые переходы капиллярной почвенной влаги из жидкого состояния и обратно с учетом коэффициента теплообмена между почвой и капиллярной почвенной влагой и теплоты плавления (замерзания) воды.

Решая уравнения (9) и (10), следует иметь в виду, что, в отличие от уравнения теплопроводимости общего вида (8), не учитываются члены, содержащие производные по пространственным переменным, так как величины коэффициентов теплопроводности k п , k л имеют порядок 10^–3, кроме того, известно из опыта, что в почве нет больших градиентов температуры. На изменение температуры почвы и капиллярной почвенной влаги в основном оказывает влияние теплообмен с некапиллярной влагой.

Для уточнения модели влагопереноса в почве отметим, что в системе уравнений (4)–(12) расчетными, т.е. подлежащими вычислению, являются величины (x, t), h(t), Z(t), T нк (x, t), T k (x, t), T п (x, t), S л (x, t). За контрольную величину примем максимальное значение высоты слоя воды из снега над почвой h = max h(t), потому что именно этой величиной определяются ограничения пропускной способности почвы. Для решения математической модели тепловлагопереноса в почве в весенний период рассмотрим случай, когда процессу замерзания подвержена только капиллярная влага, а вязкость некапиллярной влаги не изменяется в процессе ее фильтрации, тогда уравнения (4)–(7) могут быть решены независимо от уравнений (8)–(12). В любом случае система уравнений (4)–(7) может решаться независимо от уравнений (8)–(12) до тех пор, пока не замерзает вся капиллярная влага в каком-то почвенном слое, что приведет к дальнейшему уменьшению некапиллярной пористости.

Проведя анализ взаимосвязи двух составляющих частей модели влаго- и теплопе-реноса в почве, изучим уравнения (4)–(7), описывающие процессы влагопереноса как более удовлетворяющие целям нашей работы.

Из уравнений (5) и (6) следует при             .

Из уравнения (13) получим выражения для Р(x, t) :

—        ^,,(O)v(O,t)8?7

gradP(x,t) -pg - s2_x(xyR2_x(x) , или

P(x,t) = 5_та(0) ■ v(0,t) ■                 + pgYx - z(t)].            (14)

В уравнении (14) учтено, что давление в движущейся жидкости на нижней свободной поверхности X = Z(t) равно нулю. В случае постоянных значений функций S нк (х) и R нк (х) по глубине почвы уравнение (14) совпадает с законом Дарси (1).

Предположим далее, что процесс фильтрации, т.е. движение некапиллярной влаги прекращается, когда над уровнем нет слоя воды h(t) = 0 и когда нет притока талой воды q(t) = 0. Это предположение связано с тем, что в силу извилистости почвенных пор и их малого диаметра силы поверхностного натяжения способны удерживать влагу в подвешенном состоянии. Величина h(t) может стать положительной при выполнении условия

^ = lto-S.(0)-v(0,t)>0.                   (15)

В противном случае h(t) = 0.

Таким образом, ^M = ° , если

u(O,t) = q(t)/S„(O).                             (16)

С другой стороны, при отсутствии над почвой слоя воды скорость фильтрации не может превышать величину

_ S₌(O)R^(O) pg

Sri , что следует из отношения (6).

Следовательно, при выполнении условий

h(t) = 0 и_9(t)<5^(^

и согласно сделанным предположениям величина нижнего уровня насыщения некапиллярной влагой почвы Z (t) изменится по закону

^(t) = /(t)/5=^v№u.                  (18)

Рассмотрим случай, когда в процессе таяния приток q(t) преобладал над впитыванием, т.е.

q(f) > о ; _q(t) > ^_pg .

Поскольку на поверхности почвы (Х = 0) давление в жидкости должно быть равно весу столба жидкости высотой – h(t), при h(t) > 0 выполняется условие

-pgz(^ + 5^(0^(0,0877            РЗЧС .            (19)

Из уравнения (7) с помощью интегрирования по времени получим

A(t) = Jj q(u)du - J_o^z(t) S^dy ;                      (20)

где5у = 5,(у)+5ж(у).

В уравнении (20) учтены начальные условия:

/г(0) = Z(0) = 0.

Таким образом мы получим ответ на интересующий нас вопрос – определения максимально возможного уровня воды над почвой h(t), если установим зависимость величины уровня насыщения почвы Z(t) от переменной t.

Из уравнения (4) следует

S„(0)v(0,t) = 5(z(t))-^(t).                       (21)

Для установления величины Z(t) подставим значение (20) и (21) в (19), получим соотношение

5(2(0) If Вт? J^ , Лд2 , . - pgz(t) = pg £ q(u)du - pg ^^W S9y)dy > 0. (22) at u ^нх^У^нкхУ'                   ^{u                 u}

Целью следующих исследований было получение конечно-разностной схемы ре- шения задачи о влагопереносе.

Согласно общепринятой методике теории конечно-разностных схем [7–11] для величины Z(t) введем по временной переменной t разностную сетку с равномерным шагом ti = 0 ; ^-1 = t( + At;

где At – шаг сетки.

Пусть в некоторый момент времени t = ti известно значение функции Z(t); Z(t) = Z(t i ) такое, что

^ = /0^(и)^-/^5№у>0.             (23)

Для расчета величины Z i+1 = Z(t i+1 ) применим схему, основанную на аппроксимации нелинейного дифференциального уравнения в точке ^іг -^^, что соответствует второму порядку (Δt)² аппроксимации.

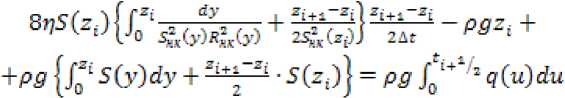
Положим

Ь(^) =

= __2^^. __. n

≥ v ^ R;x(zi) ^x(Zi)At -

MW № dy

At J° ^(у)С(у)

c(z,) = pg J_o^l+1/s q(it)du + pgz_t - pg J^S^dy = pg ■ h_t + pg J^ⁱ⁺^a q(u)du +

-pgz. > o

Тогда

a(Zi+i - 2j² + b(z_i+1 -2₄) = с .                      (28)

Следовательно из уравнения (28) находим

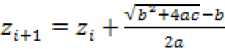
В момент времени t i+1 значение величины h i+1 выразится

^Һі+1 = Iq*¹ q(u)du - f_o^Zi+1 S(y)dy = h_t + J'¹*¹ q(u)du - ^ⁱ⁺¹ S(y)dy (30)

При условии ^i*l — 0 переходим к вычислению Z:-l по (29).

При условии ^■i-1 ^ 0 величину ^i+1 рассчитываем заново по формуле, вытека- ющей из условия

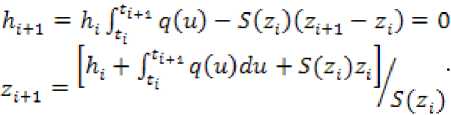
Результаты численных экспериментов могут быть проанализированы на основе сформулированных законов влагопереноса в почве в период весеннего снеготаяния. Для получения количественной выходной информации как результата решения математической задачи была составлена программа. При расчетах принималось условие, что содержащаяся с осени вода в почве находилась в замерзшем состоянии. По результатам количественных выходных данных в зависимости от изменения входной информации проведен качественный анализ контрольной для наших целей величины – максимального уровня столба воды из снега – hmax с учетом фильтрации в зависимости от разного исходного состояния почвы.

Заключение

Из анализа теоретических расчетов следует: в период весеннего снеготаяния скорость фильтрации воды в изначально мерзлую почву зависит:

• –    в большей степени от состояния пахотного слоя 0–16 см, в меньшей степени – от состояния нижнего слоя 16–50 см;

• –    от некапиллярной пористости почвы: чем выше процент некапиллярной пористости, тем больше скорость фильтрации и тем меньше уровень воды над почвой;

• –    от доли заполнения некапиллярных пор льдом, образованным при замерзании осенних осадков (осенней влажности почвы). Чем выше исходная влажность почвы, тем меньше скорость фильтрации и выше уровень надпочвенного слоя воды;

• –    от радиуса некапиллярных пор. При увеличении радиуса пор пахотного слоя почвы увеличивается скорость фильтрации и уменьшается высота столба воды над почвой.

A.S. Soyunov, N.A. Zaripova, L.S. Keruchenko

Omsk State Agrarian University named after P.A. Stolypin, Omsk

Mathematical model of thermal transfer in frozen soil