Математическая модель трехкоординатного манипулятора с параллельной кинематической структурой

На кафедре «Автоматизация механосборочного производства» Южно-Уральского государственного университета разработан механизм с параллельной кинематической структурой, выполняющий в составе лабораторного комплекса «Мехатронные устройства» роль трёхкоординатного манипулятора. Основу механизма (рис. 1) составляют три раздвижные штанги 1, 2, 3, способные изменять свою длину при помощи встроенных в них электродвигателей. Каждая штанга соединена с фланцем манипулятора 4 трехстепенным шарниром, при помощи двухстепенных шарниров штанги связаны с неподвижным основанием.

Z *

Рис. 1

Конструкция механизма обеспечивает пространственное движение манипулятора 4 вокруг неподвижной точки О - центра шарнира 5, 6. С помощью направляющей наружной поверхности, имеющей в поперечном сечении квадратную форму, манипулятор образует с внутренним кольцом 5 карданова шарнира поступательную пару, обеспечивающую изменение расстояния от характерной точки инструмента 7 до неподвижной точки О.

Одними из основных достоинств рассматриваемого механизма являются высокая жесткость и значительное усилие, развиваемое совокупным действием приводов раздвижных штанг 1,2, 3. ^                                                   Вестник ЮУрГУ, № 14, 2005

Смирнов В.А., Тверской М.М.        Математическая модель трехкоординатного манипуляторас параллельной кинематической структурой

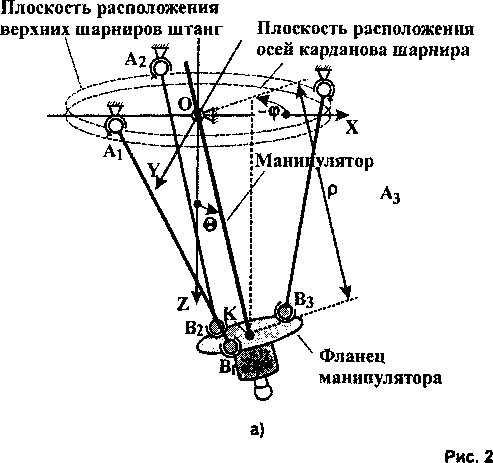
Управление механизмом осуществляется за счет изменения длин штанг. В связи с тем, что механизм содержит только три штанги, то положение манипулятора должно задаваться тремя координатами, например, координатами хк, ук, zK центра фланца манипулятора (точка К на рис. 2, а) в неподвижной системе координат OXYZ. Требуемое положение точки К может задаваться также в сферической системе координат р = [ОК], 0, ф. Пересчет сферических координат в декартовые и обратно производится с использованием следующих выражений [1]:

хк = рсо8ф8Ш0, ук = р8Шф8т0, zK = pcos0,

Р = V^XK + Ук ^+zk > ⁰ = arctg^⁴"⁵^, ф = arctg—.

ZK             хк

Найдем выражения, связывающие длины Lj штанг с заданными координатами точки К.

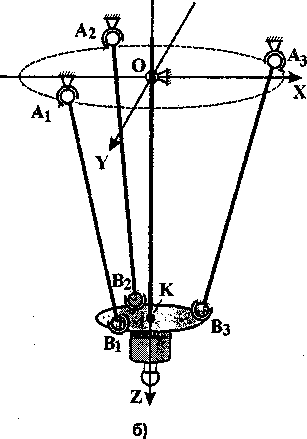
Предположим, что в начальном состоянии ось манипулятора вертикальна. Длины L, всех штанг при этом одинаковы (рис. 2, б), ось OZ проходит через центры окружностей, на которых расположены верхние (А,) и нижние (В;) шарниры штанг. Конструкция рассматриваемого механизма запрещает поворот вокруг продольной оси манипулятора, но разрешает перемещение вдоль этой оси (в начальном состоянии продольной осью является ось OZ). Поэтому переход из начального состояния (см. рис. 2, б) в требуемое (см. рис. 2, а) опишем следующим образом.

1-й этап - выдвижение манипулятора вдоль оси OZ до тех пор, пока расстояние от точки К до точки О не станет равно требуемому значению р.

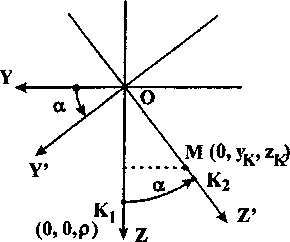
2-й этап - разворот вокруг оси ОХ . Разворот осуществляется на угол а таким образом, чтобы продольная ось манипулятора проходила через точку М с координатами (0, у_к, z_K). Введем новую систему координат OX'Y'Z' (рис. 3, а), для которой ось ОХ' совпадает с осью ОХ, ось OZ' является осью направляющего стержня, ось OY' дополняет тройку осей до правой. На рис. 3, а показан вид с положительного конца оси ОХ'.

В результате центр фланца манипулятора окажется в точке К2 с координатами (О, - psina, pcosa). Угол а может быть определен из следующего выражения:

х ук 8Шф8ш0 ■ х л                                     - tga = -— =-------= -sinф tgO .

ZK COS0                                 .

Переход от системы координат OX'Y'Z' к системе координат OXYZ будет осуществляться при помощи матрицы поворота

Расчет и конструирование

А

О О

О

Cos а sin а

О -sin а

cos а

3-й этап - разворот в точке О вокруг оси OY'. Разворот осуществляется на угол р таким образом, чтобы ось направляющего стержня проходила через точку N с координатами (х_к, у_к, z_K). Введем новую систему координат OX"Y"Z" (рис. 3, б), для которой ось OY" совпадает с осью OY', ось OZ" является осью направляющего стержня, ось ОХ" дополняет тройку осей до правой. На рис. 3, б показан вид с положительного конца оси OY".

Так как расстояние от точки N до точки О равно ^х^ + Ук +2к = Р, то в результате поворота центр фланца манипулятора совпадет с точкой N - осуществится переход в конечное состояние. Угол Р может быть определен из следующего выражения:

хк

tg₽ =

cos ф sin 6

Vyk^Zk" V^siⁿ² Фsin² 6 + cos² 6

Переход от СК OX"Y"Z" к СК OX'Y'Z' будет осуществляться при помощи матрицы поворота cosP 0 sinp

А2 -

О

О

^-sinp 0 cosPy

Рассмотренный переход центра подвижной платформы из начального состояния в конечное (требуемое) позволяет определить углы а и Р, необходимые для вычисления элементов матриц поворота А] и А2. С использованием этих матриц можно определить координаты каждого из нижних шарниров, обеспечивающие нахождение центра подвижной платформы в точке с требуемыми координатами (хк, у к, zK ):

( vkoh\

У^н

„ КОН Zn.

к в У

XBi

= A2A, y^ ■ -нач где х™4, у™4, z™4 - координаты i-ro нижнего шарнира в неподвижной системе координат СК OXYZ в начальном состоянии; Хд™, Ув°н, Zg°" - координаты i-ro нижнего шарнира в неподвижной системе координат OXYZ в конечном состоянии. Очевидно, что z™4 = ^х^ + Ук + zk =Р • Координаты х™4 и у™4 для начального состояния, показанного на рис. 3, а, легко определимы из конструкции манипулятора.

Длины шланг L;, обеспечивающие перевод центра фланца манипулятора в точку с заданными координатами (хк, у к, zK ), определяются следующими зависимостями:

L /C „конг , С . ,кон г , С „кон г , о                                       /14

i-y^Aj XBj / +VA-, Ув; ) ^\ZA| ZBj ) >1-1>3, где xA., yA., zA. - координаты верхних шарниров в неподвижной системе координат OXYZ.

Данные координаты также легко определимы из конструкции механизма.

Уравнения (1) могут быть использованы как для организации управления механизмом, так и для моделирования его поведения. При помощи этих уравнений можно определить рабочую область рассматриваемого механизма - совокупность положений некоторой характерной точки при заданных ограничениях на длины раздвижных штанг. Данная точка определяется типом инструмента, закрепленного на манипуляторе. Примем для простоты, что характерной точкой является центр фланца манипулятора. На рис. 4 показаны сечения рабочей области механизма плоскостями, перпендикулярными оси OZ, цифрами обозначены координаты z этих плоскостей. Очевид-

Смирнов В.А., Тверской М.М.

но, что обрабатываемую деталь целесообразно размещать (по координате z) в той части рабочей области, в которой площади сечений максимальны.

а)

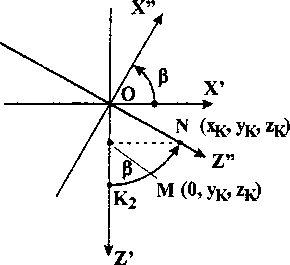
Рис. 3

При моделировании было принято, что карданов шарнир находится в плоскости расположения верхних шарниров штанг, шарниры расположены на окружностях радиусами 300 мм (верхние шарниры) и 50 мм (нижние шарниры) с угловым шагом в 120 градусов, один из верхних шарниров лежит на оси ОХ, длины штанг могут изменяться в диапазоне от 250 до 450 мм.

ya

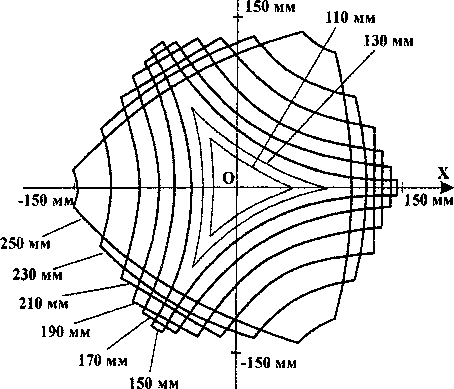
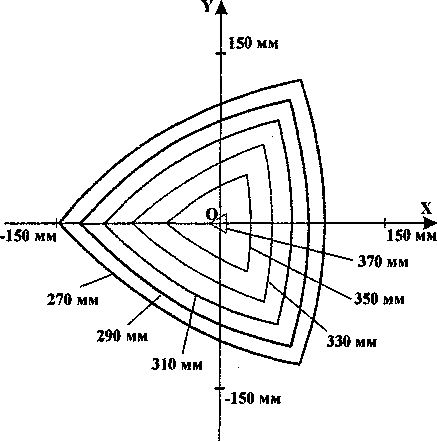
Рис. 4

Рассматриваемый механизм предназначен для выполнения сборочных или обрабатывающих операций. В любом случае представляет интерес такое управление механизмом, при котором его рабочий орган осуществляет равномерное движение по траектории, представляющей собой отрезок прямой. С точки зрения сборочных операций это позволит осуществлять основные сборочные операции вставления и надевания. При реализации какой-либо обработки такое перемещение позволит решить задачу приближенного формирования требуемой траектории с использованием линейной интерполяции [2].

Определим характер изменения длин раздвижных штанг при условии, что точка К движется по прямой из точки с координатами (х1; у,, zj в точку (х2, у2, z2). В этом случае закон изменения координат точки К во времени является линейным:

x(t) = X] +^~"t, y(t) = y] +^——t, Z(t) = Zj + —-—t.

At                  At                  At

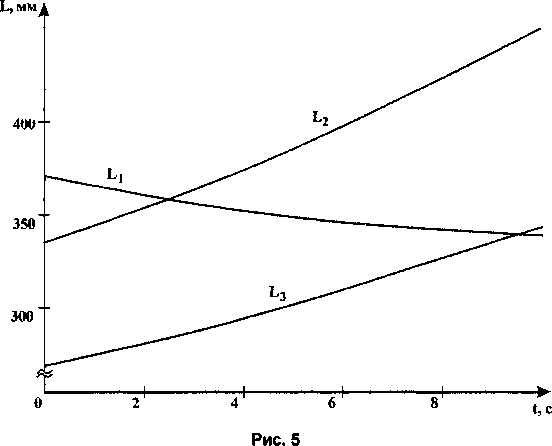
На рис. 5 показаны результаты моделирования поведения механизма в случае, когда координаты точки К должны изменяться по линейному закону от (-50,40,200) до (50,80,270).

Расчет и конструирование

Из рисунка видно, что для обеспечения линейного перемещения точки К по координатам х, у, z требуется изменение длин штанг по нелинейному закону. Это является особенностью рассматриваемого механизма.

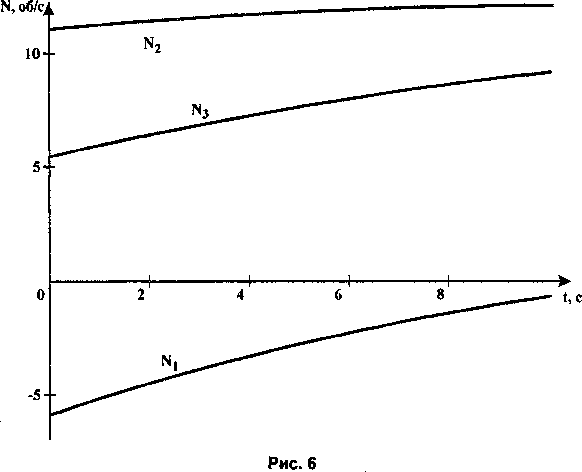
Нелинейный характер изменения длин штанг должен обеспечиваться управлением, при котором скорости электродвигателей, изменяющих длины штанг, не будут являться постоянными (рис. 6). При моделировании принято, что изменению длины штанги на 1 мм соответствует один оборот вала электродвигателя.

В дальнейшем должна быть решена задача замены непрерывных нелинейных законов изменения длин штанг механизма кусочно-линейными. Это позволит перейти к достаточно просто реализуемому управлению, при котором скорости электродвигателей, изменяющих длины штанг, будут являться кусочно-постоянными.