Математическая модель ударно-вибрационного механизма

Машины для строительства дорог с твердым покрытием используют вибрационные (погружные и поверхностные вибраторы) и ударные (трамбующий брус) механизмы для уплотнения дорожно-строительных материалов. Только совокупность этих механизмов позволяет достичь современных требований к качеству дорожного покрытия. Современные бетоно- и асфальтоукладчики имеют по несколько рабочих органов и приводов к ним, что усложняет конструкцию, увеличивает массогабаритные характеристики и, как следствие, высокую стоимость машины [1–4].

Кафедры «Колесные и гусеничные машины» и «Гидравлика и гидропневмосистемы» ЮУрГУ (г. Челябинск) разработали устройство для уплотнения труднодеформируемых (жестких) композиционных материалов – ударно-вибрационный механизм. Данный механизм позволяет воздействовать на материал как ударным, так и вибрационным методом, что позволяет получать более плотные и прочные изделия. Ударно-вибрационный механизм (рис. 1) содержит плиту нагнетателя 1, кронштейн 2, заглаживающий участок 3 плиты нагнетателя, кривошип радиусом r и маятниковый стержень. Плита нагнетателя 1 содержит с одного конца кронштейн 2, а с другого конца – заглаживающий участок 3 [5, 6].

Главным достоинством нового механизма является двукратное увеличение приводной силы, то есть усилие прессования Q , оказывающее действие на уплотняемую частицу, находится по формуле

Q = ∙ к_г ∙ ^2, (1) где P – это сила, которую развивает движитель, ^1 и ^2 – коэффициенты увеличения силы [7].

Изначально усилие, развиваемое приводом, увеличивается благодаря углу α, то есть ^1 = ; при движении кривошипа в рабочем ходе угол α увеличивается от 0 до 90, то есть коэффициент стремится к бесконечности, ^1≥1. Далее это усилие увеличивается благодаря рычагу Архимеда, то есть чем ближе частица к точке С , тем сжимающее усилие на прессуемый материал больше, и ^2 = , при а , стремящемся к нулю, коэффициент стремится к бесконечности, ^2≥1 [8, 9].

Математическая модель ударно-вибрационного механизма состоит из трех разделов: геометрического, кинематического и динамического расчетов. Исходными данными для геометрического расчета приняты [10, 11]: x ; y – расстояние от точки крепления кривошипа до точки крепления маятника по осям x и y соответственно; r – радиус кривошипа; R – радиус коромысла; R ₁ – длина шатуна; Ф – угол поворота кривошипа относительно начального положения.

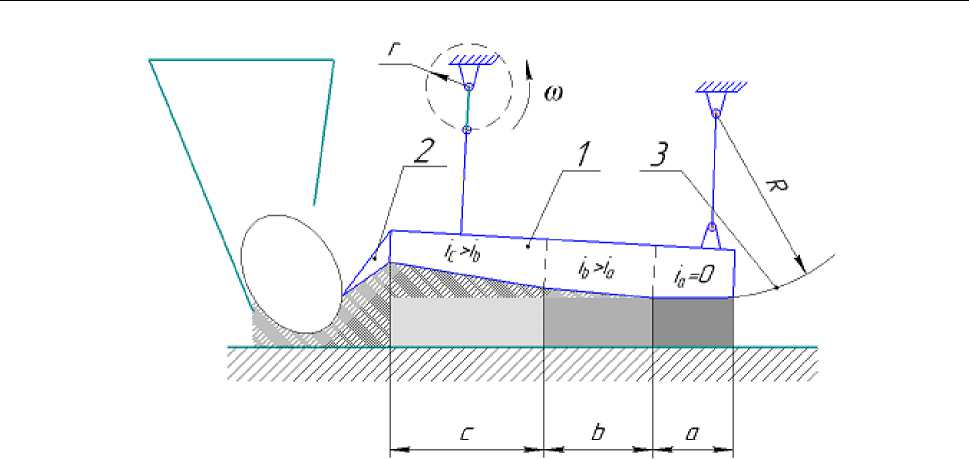
Рис. 1. Принципиальная схема ударно-вибрационного механизма

Fig. 1. Schematic diagram of the shock-vibration mechanism

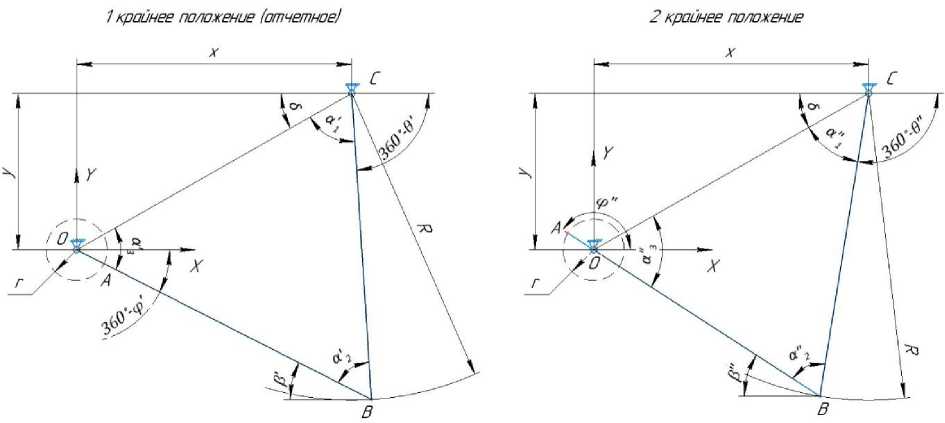
Рис. 2. Расчетная схема механизма для крайних положений Fig. 2. Calculation scheme of the mechanism for extreme positions

Первоначально исходя из основных конструктивных параметров механизма определяются 2 крайних положения, а именно переход с рабочего хода на холостой и наоборот. Расчет положения перехода из рабочего хода на холостой ход механизма:

(        )

⎧ ′=180+       +

′=

(       )

=360-

∙  ∙()

()

∙  ∙()

где 6^! ; (Г; ф' - углы отклонения коромысла, шатуна и кривошипа относительно оси Ox.

Расчет положения перехода из холостого хода на рабочий ход механизма:

()

⎧ ʺ=180++

ʺ=                  ∙ ∙((     ))-

⎩⎪  ʺ=360-              ∙ ∙((    ))      +, где 9"; Р"; ф” - углы отклонения коромысла, шатуна и кривошипа относительно оси Ox.

Расчет геометрических параметров для любого положения механизма, расчетная схема показана на рис. 3.

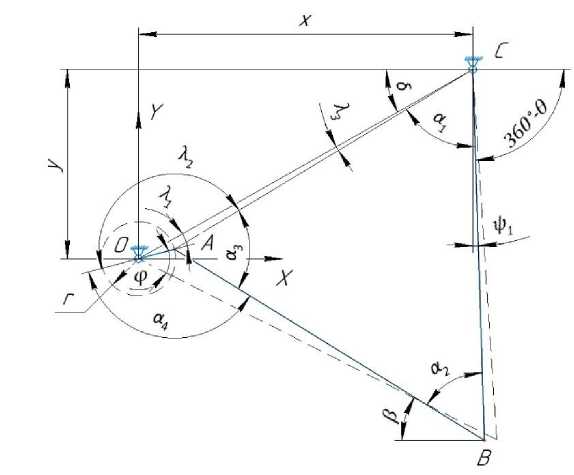
Рис. 3. Расчетная схема механизма для любого положения Fig. 3. Calculation scheme of the mechanism for any position

В ходе геометрического расчета получена итоговая система уравнений, главным результатом которой являются определения углов отклонения коромысла и шатуна относительно начального положения:

∙

⎧   Δ =-  ++

⎪                                                                                   ∙       (            )                                              ∙       ()

∆ =(   -180°)+          ∙           +            ∙  (    )

∙       (             )                                              ∙       ()

⎩                    +          +   ∙   ( ′-) , где а'!; а' з - вспомогательные углы, a<, а2; а3; а4; аs; а6 — вспомогательные коэффициенты, которые определяются по следующим уравнениям:

,             (L^+R2

=

'2\     ,                Л

;     =

(        )

=   +  ;   =2∙  ∙ ;   =

L2+Т2+R2-Й

∙

∙

;  =;  =

² ^•^ ^{1 +Г)}  /  .                 (5)

(    )                                              ∙

При этом если при расчете угол получится положительным - то коромысло смещено вправо от вертикальной оси, если отрицательным - значит, коромысло смещено влево от вертикальной оси [12, 13].

Кинематический расчет состоит из двух частей: первой частью является задача скоростей, второй частью является задача ускорений. Исходными данными являются результаты геометрического расчета и угловая скорость вращения кривошипа:

со ! = со nst - угловая скорость кривошипа.

Определим угловую скорость коромысла, продифференцировав ∆ из системы уравнений (4) относительно угла :

∙                                                                                   ∙∙

=   ∙+

∙       (            )       ∙           ∙(            )         ∙           ∙(            )         ∙           ∙()

∙                                                                                   ∙∙

+

∙       (            )       ∙           ∙(            )         ∙           ∙(            )         ∙           ∙()

Определим угловую скорость шатуна продифференцировав ∆ из системы уравнений (4) относительно угла :

∙                                                                              ∙∙

∙

∙                                                                             ∙                           ∙                                                                  ∙                           ∙                                                                 ∙∙

∙                                                                             ∙                          ∙∙

∙                                               ∙                ∙                                        ∙                ∙                                        ∙                ∙                                                         ∙          (                   )            ∙                ∙()

где   ;   ;   ;   ;   ;   ;   ;   ;   ;   ;   ;   ;   ;   ;   ;    ;      – вспомогательные коэффици енты для упрощения полученного уравнения, определяются по следующим уравнениям:

=1,5∙   ∙ ;   =-  -  ∙  ;   =0,5∙∙

=   +0,5∙   +8,5∙   ∙   +7,5∙   ∙  ;   =-17∙   ∙   -5∙   ∙  -6∙   ∙;

⎪                   =0,5∙   +6,5∙   ∙   +7∙L2∙  ;   =-3∙   ∙   -  ∙;

⎪                                                                                             , ∙      ∙          , ∙ ∙             , ∙ ∙ ∙              , ∙ ∙ ∙                                         , ∙      ∙

=                      ;=-

⎪

- /1 — а^ — а2 • а2 + 1,5 • ai • Я2 — 0,5 ' ^2 ' ^з — 2 ' ^i' ^2 ' ^з' ^4 — 0,5 ' ^1 ' ^4 — 0,375 • а2 • Я4;,, =2∙   ∙   ∙   +2∙   ∙   ∙   -3∙   ∙   +1,5∙   ∙   ∙   -0,75∙   +1,5∙   ∙∙

⎪           =1,5∙   ∙   -0,5∙   ∙   -2∙   ∙   ∙   ∙   -0,5∙   ∙   -0,5∙∙

=0,5∙   ∙   ∙   -0,25∙   +0,5∙   ∙   ∙   ;   = -0,125 ∙∙

к

=1-  -0,5∙  ;

=

-

(       ) ∙    ∙                 ∙    ∙                ∙            ∙

∙

;    =

-0,5 ∙

∙

∙

Если значение угловой скорости получится положительным – то оно направлено против часовой стрелки, если отрицательным – то по часовой стрелке.

Формулы для определения линейных скоростей [14, 15]:

∈1; ⃗ ⊥    ;    =    ∙;

∈3; ⃗ ⊥   ;    =    ∙

∈2; ⃗ = ⃗ + ⃗  ; где ⃗  ⊥   ;     =    ∙

Угловое ускорение коромысла определим, продифференцировав уравнение (6) относительно угла :

∙                                                                                   ∙                            ∙                                                                        ∙                            ∙                                                                        ∙∙

∙

∙                            ∙                                                              ∙                      ∙                                                    ∙∙

∙

∙

∙                                                               ∙                      ∙                                                     ∙                      ∙                                                     ∙                      ∙

∙                                                              ∙                      ∙                                                     ∙                      ∙                                                           ∙                      ∙

,

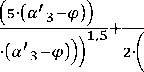
Угловое ускорение шатуна определим, продифференцировав уравнение (7) относительно угла :

91 ^∙ sin(a'₃-

∙     ∙(а'з-<р))+5з∙     ∙(a'₃-

∙     ∙(a'₃-

5

∙     ∙(а'з-<р))

£2--Wi ∙,

\    2∙|С1 + С2∙cos(a'3-tp)+c3∙     ∙(а'3-<р))+с4∙C0S^3 ∙(а'3-<р))++с5∙     ∙

,(11)

^1 + ^2 ∙cos(a'3-

3

∙     ∙(«'з-<Р))+к4∙соз(з∙(“'з-ф^+кз∙     ∙(“'з-<р))          ^!1 + ^!2∙со5(а'з-<р)+1₃∙     ∙(«'з-<Р))

2∙(/1+/2∙соз(а'з-<р)+/з∙     ∙(а'3-<р))+/4∙C0S^3 ∙(a'3-

где <91 ;У 2; 9з ; 94 ;9 s; ℎ -у ; ℎ2; ℎ3; ℎ4; ℎ5;ℎ6; /1 ; ^2 ; ^3 ;  – вспомогательные коэффициенты для упрощения полученного уравнения, определяются по следующим уравнениям:

'           51 =   ∙ с₂-2∙Ь₂ ∙ С1-2,5∙Ь₃ ∙ с₂ +3,5∙Ьз ∙ с₄+2∙Ь₂ ∙ Сз ;

5₂ =-0,5∙Ь₂ ∙ С₂ +2∙bi ∙ с₃ -4∙Ьз ∙ С1+2,5∙Ь₂ ∙ с₄+4∙Ьз ∙ Сз

⎪  5з =-1,5∙Ьз^∙с₂+3∙Ь₂^∙сз+3∙61 ^∙ с₄ ; 54 =0,5∙Ь₂^∙ с₄+4∙61 ^∙Сз^-Ьз^∙Сз ;

^⎪              0з =-0,5∙Ьз^∙ с₄ + Ь₂^∙сз ; ℎ =1,5∙d₂^∙f₂+3∙d.3^∙ /з ;

ℎ =2∙d-2 ∙ fi+2,5∙d₃ ∙ /2+2∙d-2 ∙ /3+3,5∙d-з ∙ fi ;

ℎ =0,5∙d-2 ∙ /2+2,5∙d-2 ∙A +4∙ ^3 ∙ fl+4∙ ^3 ∙ /5 ; ℎ =1,5∙ ^3 ∙ /2+3∙d-2 ∙ fs ⎪ℎ =2∙d-2^∙fl+2,5∙d.3^∙ /2+2∙d-2^∙f3+3,5∙d₃^∙ /4 ; ⎪_ℎ =0,5∙d₂ ∙ f2 +2,5∙d₂ ∙ f*+4∙d₃ ∙ fi +4∙d₃ ∙ fs ;

⎪ℎ =1,5∙d₃ ∙ /2+3∙d2 ∙ f3 ; ℎ =-0,5∙d₂ ∙h+ d₃ ∙ /3;ℎ =-d2 ∙ f3+0,5∙d₃ ∙A; ⎩           /1=1,5∙ ^6 ∙ ^2 ; ^2 =2∙ ^6 ∙ ^1 +2∙ ^6 ∙ ^3 ; /3 =0,5∙ ^6 ∙ ^2 ․

Если значение угловой скорости получится положительным – то оно направлено против часовой стрелки, если отрицательным – то по часовой стрелке.

Формулы для решения задачи ускорений:

A∈1; ⃗A= ⃗4+ ⃗Д ; где ⃗A∥OA ; ^aA =    ∙T; ^aA =0

В∈3; ⃗_B= ⃗в+ ⃗^т_в ; где ⃗в∥ВС а_в =    ∙R; ⃗в⊥ВС; о-в =   ∙R;           (13)

В∈2; ⃗в= ⃗А+ ⃗ВА + ⃗ВА ; где ⃗ВА∥ВА ; О-ВА =    ∙ Ri ; ⃗ВА⊥ВА ; ^аВА =   ∙ Ri․

Динамический расчет состоит из трех частей, первой частью является определение инерционных силовых факторов механизма для каждого из звеньев, второй частью является расчет группы Ассура II₁(2-го и 3-го звена) и третьей частью – расчет механизма I класса (1-е звено) [16, 17].

Исходными данными являются результаты геометрического, кинематического расчетов и следующие исходные:

m₄ ; m₂ ; m₃ – массы звеньев 1, 2 и 3; ^1 ; /2 ; /3 – моменты инерции звеньев 1, 2 и 3; Q(ф ) – сила, необходимая для уплотнения, равная нулю при холостом ходе, а при рабочем ходе увеличивается линейно от 0 до максимального значения в конце рабочего хода, максимальное значение определяется по формуле

Qmax = ∙s, где S – это площадь рабочей плиты, q – давление сжатия уплотняемого материала, определяемое из специализированных справочников либо экспериментально.

Определяем инерционные силовые факторы механизма для каждого из звеньев. К инерционным факторам относятся силы инерции звеньев и моменты сил инерции [18]:

инi=-mt ∙ ⃗i;Pинi₌^∙Г,

M„ui =-/. ∙ ̃;      =  ∙ ин =        ; ин =      , где ai – ускорение в центре тяжести i звена; ^i – угловое ускорение i звена; g – ускорение свободного падения.

Силовой расчет группы Ассура II1 (2, 3)

Реакцию в шарнире С и А представляем как векторную сумму нормальной силы реакции и касательной. Тогда получаем:

⎧^∑^вс = ⃗^∙R+м ин + ^⃗ ∙ℎG₃ + ^⃗_ин ∙ℎ ин =0

⎪_∑Мвс = ⃗^∙Ri +мин + ^⃗ ∙ℎС₂ + ^⃗_ин ∙ℎ ин + ⃗∙ℎ =0

∑ ⃗= ⃗с+ ^⃗ + ^⃗ + ^⃗_ин + ⃗+ ⃗_ин + ^⃗ + ^⃗ + ^⃗А =0

⎩         ∑ ⃗ = ⃗в+ ^⃗ + ^⃗_ин + ⃗с+ ⃗ =0․

Решая эту систему уравнений, мы находим реакцию в шарнире А, B и С [19].

Силовой расчет механизма I класса (1).

Реакцию в шарнире О представляем как векторную сумму нормальной силы реакции и касательной. Тогда получаем:

⃗А= ⃗I+ ⃗А; Ra = ⁽R^Ta^{) 5} +(Ra⁾ "

∑ М_о = ⃗A ∙ℎRa +Mур=0                                                (18)

∑ ⃗= ⃗Д+ ^⃗1+ ⃗0 =0․

Требуемую мощность двигателя рассчитываем по формуле [16]:

N= ур^∙to-L.

Особенностью ударно-вибрационного механизма является изменение скоростей, ускорений, сил и моментов по положению механизма. Это вызывает колебания, падения и возрастания потребной мощности, поэтому в этом механизме необходимо предусмотреть маховик. Заменяем реальный механизм на эквивалентную динамическую модель, состоящую из одного звена с приведенными моментом инерции и моментом сил сопротивления, которые находятся:

'пр=II⁺7^∙ ©^{2 +}I₂^∙ ®^{2 +}7^∙ ®^{2 +}h^∙ ®²

Mпр⁼g₂ ∙ v₂^∙ cos( ⃗^ ; ⃗ )₊Q∙ V₂^∙ cos( ⃗; ⃗ )₊G3 пр

∙

∙      ( ⃗ ; ⃗ )

,

где ^2 и ^3 – скорости в центре тяжести 2-го и 3-го звена соответственно.

По формулам (20) и (21) рассчитываем моменты инерции и моменты сил сопротивления для 12 положений кривошипа за цикл. По полученным значениям строим диаграммы моментов инерции, моментов сил, работ и энергий. Совмещая диаграмму моментов инерции и энергий, получаем график энергомасс, по которому в последствии подбираем маховик [20].

Выводы

• 1.    Ударно-вибрационный механизм обеспечивает получение направленных сдвиговых деформаций в прессуемом материале (двойное воздействие на материал); двухступенчатое увеличение усилия, развиваемого приводом, при постоянной мощности; черпание материала из бункера и его транспортировка в зону прессования; затирка рабочей поверхности прессуемого образца.

• 2.    При работе четырехзвенного механизма необходимо соблюдать следующие условия работы механизма:

• а)    максимальный угол подъема рабочего органа к поверхности прессуемого материала Y должен быть меньше 20° для лучшего прессования материала;

• б)    для повышения силы прессования в конце рабочего хода кривошип должен занимать определенное положение;

• в)    для предотвращения резких колебаний и возникновения пиковых нагрузок на валу кривошипа необходима установка маховика.

• 3.    Разработана математическая модель ударно-вибрационного механизма. В геометрическом расчете определены аналитические зависимости углов отклонения шатуна и коромысла относительно угла поворота кривошипа и другие геометрические характеристики четырехзвенного механизма. В кинематическом расчете определены зависимости угловых скоростей и ускорений

звеньев механизма, скорости и ускорения в особых точках относительно угла поворота кривошипа. В динамическом расчете определены усилие, необходимое для сжатия, реакции в шарнирах механизма, уравновешивающий крутящий момент на кривошипе и необходимая мощность на кривошипе.