Математическая модель установившегося поворота гусеничного трелевочного трактора

Гусеничный движитель получил широкое распространение на лесозаготовительных машинах. Такие качества, как повышенная проходимость по слабым грунтам, значительное удельное сцепление с поверхностью пути и другие, обретаемые благодаря гусеничному движителю, обусловили в настоящее время его преимущественное использование на отечественных лесопромышленных тракторах.

Движение по волокам и лесосекам связано с частыми и крутыми поворотами. Поворот входит в технологическую схему как прием при сборе пачки (трелевочная машина) и формировании пакета деревьев (валочно-пакетирующая машина). В настоящее время уже применяются механизмы поворота в виде полнопоточной гидрообъемной трансмиссии по бортовой схеме. Такая схема трансмиссии позволяет свести к минимуму тормозные потери, присущие механизмам поворота с фрикционными устройствами для дополнительного торможения отстающей гусеницы.

В этой связи исследование кинематики, динамики и затрат мощности при повороте гусеничной лесозаготовительной машины, оборудованной механизмом поворота, в качестве которого выступает гидрообъем-ная трансмиссия, выполненная по бортовой схеме, является весьма актуальной задачей.

ВХОДНЫЕ ВЕЛИЧИНЫ

В качестве входных величин, входящих в математическую модель, используются:

• -    конструктивные параметры трактора (колея трактора, длина опорной поверхности гусеницы, ширина гусеницы, координаты центра масс; координаты точки приложения крюковой силы);

• -    внешние силы (вес трактора, вес пакета, крюковая сила; сила инерции);

• -    параметры грунта (коэффициент внешнего трения; коэффициент внутреннего трения, буксование; объемный вес грунта).

ДОПУЩЕНИЯ

При построении математической модели принимались следующие допущения:

• -    давление трактора на грунт распределено равномерно по длине опорной поверхности;

• -    связь между нормальным давлением на грунт q и вертикальной деформацией h описывается идеализированной моделью Горячкина –Летошнева;

• -    гусеничное звено представляем в виде плоского прямоугольника с размерами сторон, равными ширине и длине звена.

КИНЕМАТИКА

Определение линейных и угловых скоростей (рис. 1) и ускорений гусеничного трактора, оборудованного полнопоточной гидрообъемной трансмиссией по бортовой схеме. Как известно, теоретическая угловая скорость поворота трактора

ωTt =(υ2t-υ1t)/B=ωдв(1 - 1)⋅rзв , i2 i1 B где ωдв – частота вращения коленчатого вала ДВС; 11

,   – кинематические передаточные отношения до

• i ₂    i ₁

ведущих звездочек соответственно забегающего и отстающего бортов ( i ₂, i ₁ – кинематические передаточные числа); r_зв – радиус ведущей звездочки; В – колея трактора.

Устанавливаемые передаточные отношения отстающего и забегающего бортов определяются параметрами регулирования гидронасосов и объемными КПД гидромашин

^{=      ⋅ λ} 1 ^⋅ η он 1 ^⋅ η ом 1 ;

• i 1     i мех

^{=     ⋅ λ} 2 ^⋅ η он 2 ^⋅ η ом 2 ,

• i 2     i мех

где i_мех – передаточное число механической части трансмиссии; η_он , η_ом – объемные КПД гидроагрегатов; λ – параметр регулирования гидронасоса, λ = q_i / q _max ( q_i – текущий, q _max – максимальный объем рабочей камеры гидронасоса); r_зв – радиус ведущей звездочки.

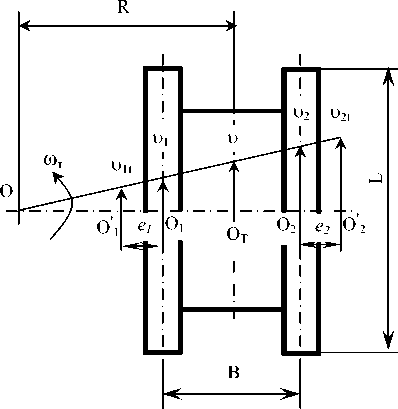
Рис.1. Схема кинематики поворота (режим скольжения отстающей гусеницы)

Тогда t ωдв              rзв   ωдв             rзв

ωT =    λ2ηoн2ηом2    -    λ1ηoн1ηом1

i мех             B   i мех

⁼ ω ^дв r^зв ( ^λ 2 η он 2 η ом 2 ^{- λ} 1 η он 1 η ом 1 ) .

i мех B

Теоретическая линейная скорость трактора

υ +υω

υ ct ^{= 2 t    1 t = дв} [ ^λ 2 η oн 2 η ом 2 ^{+ λ} 1 η oн 1 η ом 1 ] ^⋅ r зв .

2      2 i _мех

Теоретическое центростремительное ускорение

υ2

j ct ^{=    =}      [     ( ^λ 2 η oн 2 η ом 2 ^{+ λ} 1 η oн 1 η ом 1 ) r зв ] .

R    4 R i_мех

Здесь R – радиус поворота.

Действительная угловая скорость поворота трактора

ωТ = ωдв rзв (λ2ηон2ηом2(1-δ2) -λ1ηон1ηом1(1±δ1)) , iмех B где δ – буксование.

Действительная линейная скорость трактора

= υ2 + υ1 = c2

= ^{ω дв} [ λ ₂ η _{oн 2} η _{ом 2}(1 - δ ₂) + λ ₁ η _{oн 1} η _{ом 1}(1 ± δ ₁)] ⋅ r_зв .

2 i мех

( q _{2 i} = const ), то гидротрансмиссия работает как механизм поворота второго типа (скорость прямолинейного движения сохраняется на забегающей гусенице). Для этого случая исходя из предположения о равенстве текущего объема рабочей камеры гидронасоса забегающего борта максимальному объему рабочей камеры ( q _{2 i} = q _max и λ ₂ = λ ₀ = 1 , т. е. до входа в поворот движение происходило при максимальной подаче гидронасоса) формулы для определения кинематических параметров можно представить в следующем виде: угловая скорость

ω _Т = ^{ω дв} r^зв ( η _{он 2} η _{ом 2}(1 - δ ₂) - λ ₁ η _{он 1} η _{ом 1}(1 ± δ ₁)) ;

i мех B линейная скорость

υ _c = ^{ω дв} [ η _{oн 2} η _{ом 2}(1 - δ ₂) + λ ₁ η _{oн 1} η _{ом 1}(1 ± δ ₁)] ⋅ r_зв ;

2i мех центростремительное ускорение jc =    [ дв (ηoн2ηом2(1 -δ2) + λ1ηoн1ηом1(1 ±δ1))rзв ]2

мех

Таким образом, при кинематическом регулировании линейные скорости определяются параметрами регулирования, объемными КПД гидроагрегатов и свойствами грунта.

ДИНАМИКА

При повороте гусеничной трелевочной машины в ходе перемещения пакета деревьев (хлыстов) происходит перераспределение нагрузок между гусеницами за счет изменения направления действия крюковой силы от части пакета, волочащейся по грунту, – появления поперечной составляющей крюковой силы (рис. 2).

Опорные реакции i- й гусеницы

Zi = Zпрям - (-1)i ⋅ ΔZпоп , реакция при прямолинейном движении

Z прям = 2 (GT + Q1 + Pкр sin β) , величина перераспределения (рис. 3)

h кр                  h

ΔZ   = P     cos βsinγ - P с поп кр B               j B или

1    hh

Z 1 = 2 ( G T + Q 1 + P кр sin β ) + P кр B cos β sin γ - P j B ^с ;

Если в режиме поворота объем рабочей камеры гидронасоса забегающего борта не изменяется

1                                 h кр                   h

Z 2 = ( G T + Q 1 ^{+ Р} кр sin ^{в )} - ^Р кр "^cOs ^e siⁿ / ⁺ Pj — .

2     BB

Здесь G_T – вес трактора; Q ₁ – вес части пакета, размещенной на тракторе; P_кр – крюковая нагрузка; P_j – сила инерции; в - угол между линией действия крюковой силы и поверхностью движения; у - угол между продольной осью машины и пакетом деревьев; h_кр – вертикальная координата приложения крюковой силы; h_с – вертикальная координата центра масс.

^- f_cqb

г

e 2 ln

I------Г A

.     . 4 e 2

^{1 + 1 +}

2 e 2 ²

L

V             7

f 1+

+ e ² In

I------Г A

. 4 e 2 ²

² e 2

L

.

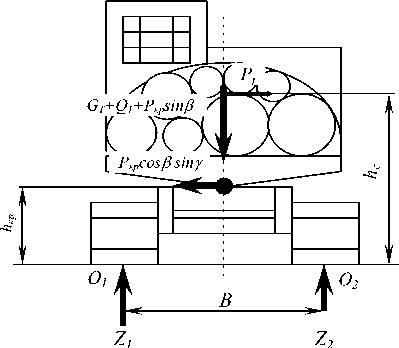
Рис. 2. Схема определения опорных реакций

Здесь f_c – коэффициент трения сталь – почва; q – давление гусеницы на грунт; b – ширина гусеницы; L – длина опорной поверхности; e ₁ , e ₂ – величины поперечного смещения полюсов вращения отстающей и забегающей гусениц;

2) момент сопротивления от перемещения вала срезанного грунта M_нг :

M нг

= f п • Y r • h •

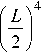
( 1 - 5 2 ) 2 ,    ( 1 + 5 _X ) ²

4 •[ R + B | 4 •[ R - B |

V 2 7 V 2 7

Здесь f п - коэффициент внутреннего трения; у г -объемный вес грунта; h – глубина колеи.

3) момент сопротивления при деформации грунта кромками гусениц M_см

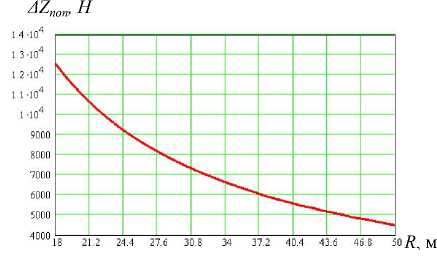
Рис. 3. График зависимости изменения опорных реакций на гусеницы от радиуса поворота

м см = 2 bT 0

L ² +1 2^ ⁴      ( 1 — 5 2 ) ²

I Kt

+

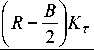
⁽ 1 + 5 1 ^{) 2}

e

-1

+

( 1 + 5 1 ) 2

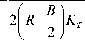
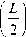
- 1

Составляющие момента сопротивления повороту M_C :

1) момент сопротивления при скольжении опорной поверхности гусеницы по грунту M_T

MT

L ²

= f c qb _Т

' 1 + "^ + 1 + 4 e 1-

L ²   V     L ²

4 e ₂ ²

Здесь т о - предельное значение сопротивления грунта смятию и срезу; К _т - параметр, характеризующий деформируемость грунта (пористость).

Тогда суммарный момент сопротивления повороту

MC = MT + Mнг + Mсм.

График зависимости суммарного момента сопротивления повороту от радиуса представлен на рисунке 4.

Результирующий момент сопротивления повороту (с учетом сопротивления в результате взаимодействия пакета с погрузочным устройством)

^Mрез = ^MC + ^Ркр • ¹ • sin Y • cos ^в

Необходимые касательные силы тяги

1                                   h _кр

^P k 2 = ^f • ^[^⁽ G T + Q 1 + ^Р кр sin P ) - ^Р кр B" cos I sin Y +

Мощность внешних сопротивлений представим в зависимости от мощности, потребной для прямолинейного движения машины до входа в поворот [1]:

N o = N пр

Р + Ч гр p + q k

или пр

p ⁺ q гр p ⁺ qk ’

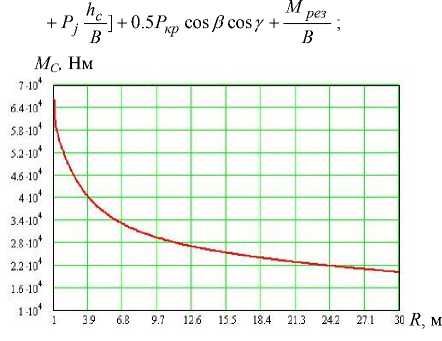
Рис. 4. График зависимости суммарного момента сопротивления повороту от радиуса (летний волок, холостой ход)

1                                   h кр

Pk 1 = f • [~(GT + Q1 + Ркр sine) + Ркр —^cosesinY - h                     M рез

- P — ] + 0.5 P „cos в cos y---— j B кр                B

Графики зависимости касательных сил тяги от радиуса поворота представлены на рисунке 5.

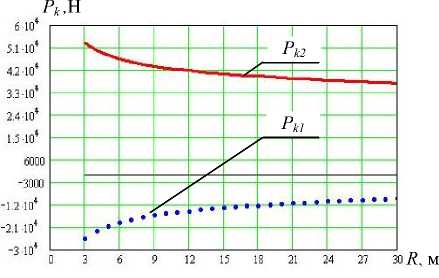
Рис. 5. Графики зависимости касательных сил тяги от радиуса поворота (летний волок, грузовой режим)

МОЩНОСТЬ

Мощность, необходимая для поворота, расходуется на преодоление внешних и внутренних сопротивлений

Nnoe = NO + NT , где NO – мощность, расходуемая на преодоление внешних сопротивлений; NT – тормозная мощность (мощность, затрачиваемая на трение в буксующем фрикционном элементе).

M где q2p - основной параметр поворота, q2p =---— ;

гр                                         гр Ркп • B p = R / B - относительный радиус поворота; Ркп - геометрическая сумма касательных сил тяги отстающей и забегающей гусениц; qk – основной параметр механизма поворота, qk = 0,5 для механизмов поворота второго типа (бортовые фрикционы, одноступенчатые планетарные механизмы поворота); qk > 0,5 для механизмов поворота третьего типа.

Графики зависимости мощности, необходимой для поворота N_пов = f ( R ) от радиуса для различных типов механизмов поворота, представлены на рисунке 6.

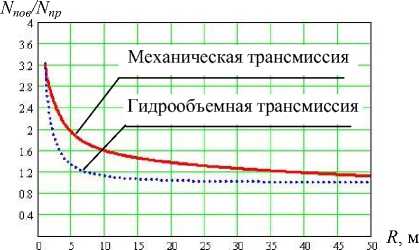
Рис. 6. Сравнительные графики затрат мощности при повороте тракторов с механической и гидрообъемной трансмиссией, построенные на основании модели

ВЫВОДЫ

• 1.    Разработанная математическая модель движения гусеничного трелевочного трактора, описывающая кинематику и динамику установившегося поворота, позволяет определять затраты мощности при повороте машин с различными типами трансмиссий (механизмов поворота).

• 2.    Результаты моделирования показывают, что затраты мощности при повороте гусеничного трелевочного трактора возрастают с уменьшением радиуса поворота, причем мощность, необходимая для поворота трактора с гидрообъемной трансмиссией, на 15 … 20 % ниже мощности, необходимой для поворота трактора с механической трансмиссией (при малых радиусах).