Математическая модель восстановления техногенной пустоши
Автор: Хоменко И.Е., Колпак Е.П.
Журнал: Международный журнал гуманитарных и естественных наук @intjournal
Рубрика: Физико-математические науки
Статья в выпуске: 10-3 (97), 2024 года.
Бесплатный доступ
Экономическая деятельность человека сопровождается изменением экологической обстановки в зоне расположения крупных промышленных центров. Одной из задач математического моделирования является поиск рациональных вариантов восстановления экосистемы после снятия антропогенной нагрузки. В работе разработана математическая модель «зарастания» техногенной пустоши растительностью, представленная начально-краевой задачей для уравнения переноса. Приведена оценка линейной скорости распространения растительности. Дано вероятностное распределение покрытия территории растительностью. Математическая модель построена на основе дифференциальных уравнений в частных производных.
Выживаемость, математическая модель, популяция, техногенная пустошь, растительность, дифференциальные уравнения
Короткий адрес: https://sciup.org/170206982
IDR: 170206982 | DOI: 10.24412/2500-1000-2024-10-3-74-79
Текст научной статьи Математическая модель восстановления техногенной пустоши
Металлургическое производство сопровождается выбросами в атмосферу кислотных окислов и металлов, выпадения которых на поверхность земли приводит к гибели флоры и фауны. На значительных расстояниях от точек выбросов территория превращается в пустошь. На окраинах пустошей проективное покрытие растительного покрова не превышает 0,1-0,5% [1]. По мере удаления от источника загрязнения численность видов увеличивается вплоть до естественных значений, которые характерны для «чистых» территорий.
Загрязнители территории, такие как тяжелые металлы (медь, никель, цинк, кадмий, свинец) могут сохраняться в почве многие десятилетия. Так, например, медь и цинк растворяются или выносятся из почвы на протяжении около 300 лет, а свинец - около 1 000 лет [2]. Часть загрязнителей включается в трофические цепи, оказывая тем самым стрессовое давление на все живое. После прекращения загрязнения территории естественное восстановление растительного покрова без очистки почв от полютантов невозможно [3]. Хемофитостабилизация, как способ очистки территории, улучшает свойства почв, но не уменьшает содержание доступных растительности полютантов до допустимого уровня. Наиболее эффективным, но и дорогим, способом восстановления пустошей является реме- диация путем нанесения на поверхность загрязненных почв плодородного слоя [3].
В математической модели предполагается, что техногенная пустошь после хемофитостабилизация начинает зарастать растительностью. Распространение растительного покрова на частично очищенной территории начинается от границы между пустошью и прилагающей к ней не нарушенной зоной. Часть полютантов в почве после ее восстановления сохраняется, но в значительно меньших концентрациях, чем на незагрязненной территории. Изменение их концентрации растет по экспоненциальной зависимости от границы пустоши до точки выбросов [2].
Траектория распространения растительности в математической модели представлена отрезком длиной l . Растительность движется за счет расширения корневой системы и распространения семян растений на небольшие от растений расстояния.
Пусть рост растительности в конкретной точке отрезка описывается логистическим уравнением [4], а ее распространение вдоль отрезка происходит за счет линейного смещения [5]. С учетом этих предположений модель распространения растительного покрова на «чистой» территории представлена дифференциальным уравнением в частных производных [5].
d u д t
д u
д x
(.
ци 1 - к
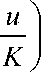
где и - линейная плотность фитомассы, v - линейная скорость движения растительности, ц - удельная скорость увеличения объемов фитомассы, K - плотность фитомассы в равновесном состоянии (емкость среды, [4]). В дальнейшем за единицу измерения принимается емкость среды, то есть считается, что K = 1 .
Распределение полютантов вдоль траектории описывается экспоненциальной зависимостью с максимальным значением в точке расположения источника загрязнения [2], убылью по направлению к границе пустоши. Предполагается, что удельная скорость роста фитомассы уменьшается с увеличением концентрации полютантов, уменьшается и линейная емкость среды, и линейнная скорость движения границы пустоши. С учетом этих предположений модель зарастания «чистой» территории (1) переходит в модель зарастания «загрязненной» территории:
д и д / ax \ ( . — = - v—(e и ) + ци e дt дx^ 1 к
где а - параметр.
Модель (2) нормирована таким образом, что при а = 0 она переходит в модель (1). Предполагается, что граница «пустоши» рас- положена в точке x = 0, а источник загрязнения находился в точке x = l.
Заселение территории начинается от точки x = 0 . Этому условию соответствует граничное условие при x = 0
du
— = ци (1 - и )- vu.
Предполагается, что из этой точке часть растительности смещается по направлению к точке x = l .
Начальное условие при x = 0
и = uQ, где и0 << 1, означает, что восстановление территории Уравнение (3) имеет две стационарные начинается с малого количества фитомассы. точки
и = 0 и и = 1--.
ц
Вторая точка реализуется, если выполняется неравенство v < ц . в этом случае эта точка будет устойчивой. Поэтому растительность будет распространяться вдоль отрезка, если скорость ее распространения не будет превышать удельную скорость роста.
В отсутствие полютантов (при а = 0 в (2)) при достаточно больших временах (при t = да ) уравнению (3) удовлетворяет функция
u =
A
и exp —x
A
1 - и* + и* exp — x
,
v где и* = 1--.
A
При x ^ да , как следует из (4) и Ч 1 , то есть со временем покрытие территории растительностью будет близко к проективному покрытию.
Стационарное распределение значений функции и(t = да, x) находится как решение уравнения v—( е ™и ) = ^и дxv ’
e ax
u
e " ax
v
.
с граничным условием при x = 0 : и = 1--
A
С учетом этого в этой точке
du X
— =(1 + a) 1 dx {
^-
v
> 0 .
То есть функция и ( x ) в окрестности этой точки растет с ростом x .
Уравнение (5) преобразуется к виду du
— = и dx
A(1 - ие2 ax
) + a .
При x ^ да правая часть уравнения (6) должна принимать отрицательные значения. Из этого следует оценка значения функции и ( t = да , x )
е ~2ах
v
1 + a— < и(t = да,x).
Таким образом, модель (2) допускает зарастание территории в окрестности источника загрязнения.
Решение нелинейного уравнения (2) строится с применением численных методов. Дис- кретизация дифференциального уравнения на равномерной пространственной сетке с шагом h, временной сетке с шагом т приводит к системе алгебраических уравнений
Ui = u 0,
U — U =—tvu^ + TjUu^ (1 — u^ ),
k ui k
—
k — i
u
e — ax ( u k — u — )
—tv------------ h
। k — 1 „— ax
+ tluu e
—
ui
k
e ax
i = 2,3,...
где u k - значение сеточной функции в i -ом узле в дискретный момент времени k . Используется неявная схема аппроксимации производных [4]. Временной шаг выбирался tv из условия — < 0.2. Этим обеспечивается сходимость последовательности (6) к решению уравнения (2).
Решение уравнений (7) строилось для единичного отрезка ( 0 < x < 1 ). Принималось, что источник загрязнения находится в точке x = 1 . Движение растительности, появившейся в точке x = 0 , происходит по направлению к точке x = 1 . Параметры ^ , v и а выбирались из диапазонов: а е (0.1,0.3) ,
^е (0.02,0.08), v е (0.001,0.005). Значения параметров соответствуют данным приведенным в [2, 3], но применительно к модели импактной зоны единичной длины. Скорости роста растительности оценивались по данным, приведенным в [6, 7]. За единицу времени приняты 30 суток. Выбранный диапазон параметров соответствует росту различных трав и кустарничков.
На рисунке 1 приведено изменение функции u ( t , x ) вдоль координаты в моменты времени t = 35 и t = 175 для параметров а = 1.5 , ^ = 0.08 , v = 0.005 . Пунктирной линией отмечено решение уравнения (2). Шаг по пространственной сетке принимался равным 0.004, а по временной – 0.2.
Имитационная модель вероятности распределения покрытой растительностью площади в момент времени t = 175 (рис. 2) строилась на основе выбора случайным образом параметров ^ , v и а из заданных диапазонов 1 000 раз.
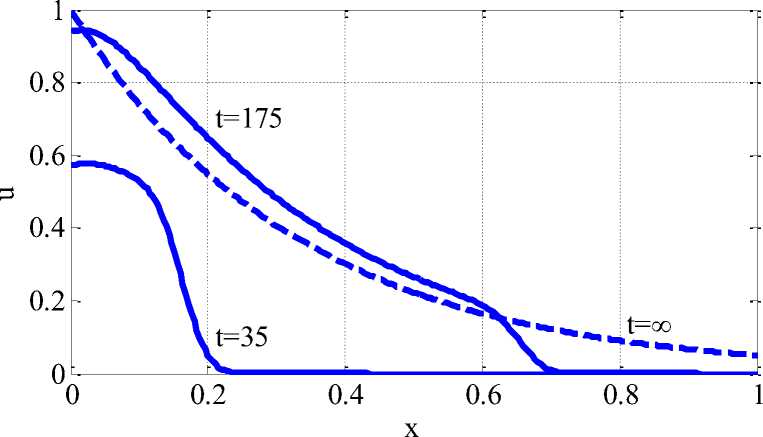
Рис. 1. Зависимость функции u ( t , x ) от x в моменты времени t = 35 , t = 175 и t = ®
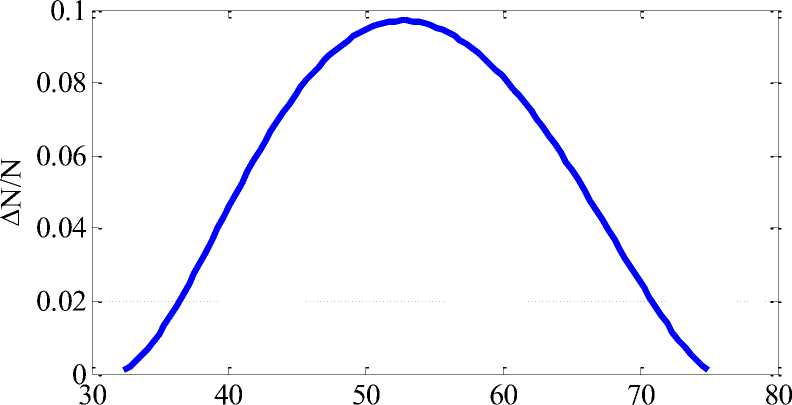
Покрытие (%)
Рис. 2. Вероятность распределения покрытой растительностью площади в момент времени t = 175
Как следует из анализа полученных результатов, наличие полютантов на почве после хемофитостабилизации не позволяет растительности со временем покрыть всю пустошь до проективного значения. Применительно к импактной зоне Мончегорского мед-но-никелевого комбината, как следует из данных приведенных в [2, 6, 7], пустошь распространяется на 10-15 км. С учетом полученных результатов (рис. 1), через 15 лет после закрытия источника загрязнения в радиусе около 3 км растительность еще не появится. Наиболее вероятное покрытие будет составлять около 55% (рис. 2) от естественной, не подверженной загрязнению территории. Та- менные оценки могут быть использованы на стадии проектирования очистки территорий [8].
Хемофитостабилизация не удаляет полю-танты из почвы. Более эффективным способом восстановления пустошей является ремедиация путем нанесения на поверхность загрязненных почв плодородного слоя. В этом случае модели зарастания пустоши соответствует модель (1). При ремедиации вместе с плодородной почвой на пустошь могут вноситься и различные виды растений. Естественно рациональнее, чтобы эти виды не составляли конкуренцию видам, проживающим на окраинах пустоши.
кие теоретические пространственные и вре-
Список литературы Математическая модель восстановления техногенной пустоши
- Коротков В.Н., Копцик Г.Н., Смирнова И.Е., Копцик С.В. Восстановление растительности на техногенных пустошах в окрестностях Мончегорска (Мурманская область, Россия) // Russian Journal of Ecosystem. - 2019. - Vol. 4 (1). - С. 1-18. DOI: 10.21685/2500-0578-2019-1-4
- Гончарова А.Б., Колпак Е.П., Гасратова Н.А. Модели антропогенного давления на экосистему Учебное пособие / Санкт-Петербургский государственный университет. - Казань, 2024. - 102 с. EDN: FNFHYS
- Копцик Г.Н., Копцик С.В., Смирнова И.Е. Эффективность ремедиации техногенных пустошей вблизи комбината "Печенганикель" в Кольской Субарктике // Почвоведение. - 2013. - №10. - С. 1263-1273. EDN: QZXDHF
- Колпак Е.П., Гончарова А.Б., Гасратова Н.А. Имитационные модели одиночной популяции Учебное пособие / Санкт-Петербургский государственный университет. - Казань, 2024. - 112 с. EDN: CPPFKI
- Гончарова А.Б., Колпак Е.П., Виль М.Ю., Абрамова А.В., Бусько Е.А. Математическое моделирование злокачественных опухолей яичников // Вестник Санкт-Петербургского университета. Прикладная математика. Информатика. Процессы управления. - 2022. - Т. 18. - № 1. - С. 120-134. EDN: OMBJJZ
- Черненькова Т.В. Реакция лесной растительности на промышленное загрязнение. - М.: Наука, 2002. - 191 с. EDN: RECOQV
- Ярмишко В.Т., Игнатьева О.В. Многолетний импактный мониторинг состояния сосновых лесов в центральной части Кольского полуострова // Известия РАН. Серия биологическая. - 2019. - № 6. - С. 658-668. DOI: 10.1134/S0002332919060134 EDN: UNOGEE
- Кривополенова С.Д., Гончарова А.Б. Первичный анализ данных для построения системы поддержки принятия решений Процессы управления и устойчивость. - 2019. - Т. 6. - № 1. - С. 250-254. EDN: DSXDBJ


