Математическая модель выбора параметров экраноплана на стадии технического предложения

Проект нового экраноплана на этапе технического предложения должен отражать результаты проектно-конструкторских изысканий рациональных параметров эк-раноплана. Под рациональными параметрами понимаются такие, которые наилучшим образом отвечают поставленным тактико-техническим требованиям и техническому заданию. Выбор рациональных параметров летательного аппарата, рассмотренный в работах [1; 2; 3], позволяет решать задачи многопараметрической оптимизации, где в качестве целевой функции Ф = f ( A , f ) принимают либо приведенные затраты, либо критерий, отражающий устойчивость летательного аппарата.

Задачу выбора рациональных параметров экраноп-лана необходимо рассматривать как многофункциональную, поскольку требуется при проектировании обеспечить максимальное аэродинамическое качество, устойчивость аппарата, минимальную массу конструкции, минимальные приведенные затраты, минимальное лобовое сопротивление.

Существующие методы оптимизации, основанные на свертывании векторного критерия целевых функций и перехода к одноцелевой задаче, приводят к замене одной задачи другой, а получаемое решение не соответствует исходной постановке. Поэтому решать данную задачу необходимо методом, позволяющим учитывать несколько целевых функций, решать задачу в исходной постановке - методом исследования пространства параметров (ИПП).

В данном случае математическая модель была построена для трех основных компоновочных схем, «самолетной», «утка», «гибридная», и трех видов несущих поверхностей треугольное с углом поперечного V < 0, треугольное с углом поперечного V > 0 [4], прямоугольное (рис. 1).

Рис. 1. Основные аэродинамические компоновки экранопланов

Сформулируем задачу выбора рациональных параметров экраноплана.

Варьируемые параметры:

• -    удлинения несущих поверхностей X , , X₂, ..., X n ;

• -    вынос дополнительных несущих поверхностей, переднего горизонтального оперения, относительно крыла L , , L 2 ,^, L n ;

• -    вынос по высоте дополнительных несущих поверхностей, переднего горизонтального оперения, горизонтального оперения относительно крыла h ,, h ₂, ..., h n ;

• -    угол установки дополнительных несущих поверхностей, переднего горизонтального оперения, горизонтального оперения относительно крыла Aa ,, Аа ₂, ..., Aa n ;

• -    относительная площадь дополнительных несущих поверхностей, переднего горизонтального оперения, горизонтального оперения S , , S ₂, _, S_n .

Целевые функции:

• -    аэродинамические коэффициенты;

• -    массовая целевая функция;

• -    характеристики силовой установки;

• -    технико-экономические показатели.

Функциональное ограничение - продольная устойчивость; критерии качества.

Получим теперь математическую модель, связывающую варьируемые параметры с целевыми функциями. Для этого сначала необходимо получить функциональные зависимости c y = fа , h ), m_z = fа , h ), x_f = fа , h ) для трех компоновочных схем.

Методом дискретных вихрей решались линейные задачи стационарного безотрывного обтекания несжимаемой жидкостью системы тонких несущих поверхностей, конечного размаха прямоугольной формы в плане. Результат решения данных задач: численные значения аэродинамических коэффициентов c y ( а , h ) и m_z ( а , h ), относительной координаты аэродинамического фокуса х(а , h ), распределение аэродинамической нагрузки по несущей поверхности для трех аэродинамических схем несущих поверхностей «самолетная», «утка», «гибрид».

По полученным числовым значениям коэффициента продольного момента, подъемной силы, безразмерной координаты фокуса аппарата относительно крыла методом интерполяции функции нескольких переменных получены функциональные зависимости с у = f(а , h ), m_z = fа , h ), x_F = fa , h ) для компоновки «утка»:

• -    коэффициент подъемной силы:

C y ( a , h ) = - ,,729 5 ^{b нг}°/ ( C yo ( A , H ) +

а

+ C yo ( a , h )) - 0,032 39 L _Hro ( C yo ( A , H ) + C yo ( a , h )) -

• - 0,020 34 а нго ( C yo ( A , H ) + C yo ( a , h )) -- 4,498 82 h нго ( C yo ( A , H ) + C yo ( a , h )) +

+0,034 03,bнУ Lнго (Cyo (A, H) + Cyo (a, h)) - а

• - 0,007 26 ^b ну а нго ( C yo ( A , H ) + C yo ( a , h )) + а

• +,6,659 57b-V hнго(Cyo(A,H) + а
• +Cyo (a, h)) - 0,002 348Lнгоа(Cyo (A, H) + Cyo (a, h)) + +0,200 428Lнгоhнго (Cyo (A, H) + Cyo (a, h)) + +,, 046 6,8анГо hнго (Cyo (A, H) + Cyo (a, h)) +

+ 4,496 74 4 1 ^{Ь нг}°4 I ( C yo ( A , H ) +

+ C yo ( a , h )) + 0,003 ,72 L^ ( C yo ( A , H ) + C yo ( a , h )) -- 0,000 5 ! а 2, ( C yo ( A , H ) + C yo ( a , h )) - - 435,58, h н_то ( C yo ( a , h ) + C yo ( A , H )) -

• - 22,, 940 5 1 ^b I h нго ( C yo ( A , H ) + C yo ( a , h )) + V / ^U а 7

+ , 022,288 1 ^b ™V I h н ² го ( C yo ( A , H ) + C yo ( a , h )) -

V / ^U а 7

- 586,298 1 bну, h нго I ( C yo ( A , H ) + V а 7

^{+ C} yo ⁽ a , ^h )) ^{+ C} yo ^{( A} , ^H ) ^{+ C} yo ⁽ a , ^h );

- коэффициент продольного момента:

m_z ( a , h ) = 0,956 445 b нгу ^ ( m_zo ( A , H ) +

⁺ m zo ^{( a} , ^h )) ^{- 0,869 02 L} нго ⁽ m zo ⁽ A , ^H ) ⁺ m zo ^{( a} , ^h )) ^-

- 0,087 72 а нго ( m_m ( A , H ) + m_Z o ( a , h )) +

+ 80,359 2, h н _Г о ( m_Z o ( A , H ) + m_m ( a , h )) -- ,,,45 2, ^Ьну_Ьа L нго ( m zo ( A , H ) + m_zo ( a , h )) -- 0,059 27 b нгУ а^ а нго ( m zo ( A , H ) + m_m ( a , h )) -

- 0,,49 b но / h нго ( m zo ( A , H ) + C yo ( a , h )) + + 0,0,9 259 L . нго а ( m_Z o ( A , H ) + m_m ( a , h )) -

- ,0,98,3 L нго h нго ( m_m ( A , H ) + m_Z o ( a , h )) -

- 3,744 83 а нго h нго ( m_zo ( A , H ) + m_zo ( a , h )) - ²

- 2,985 42 1 ^Ьнго/_ь I ( m zo ( A , H ) + m_zo ( a , h )) + V а 7

+ 0,078 725 L H _Г о ( m_m ( A , H ) + m_Z o ( a , h )) + + 0,0,2 ,38 а нго ( m_m ( A , H ) + m_Z o ( a , h )) - -

1 ⁶³ 1 ^,3 6 ^h нго ⁽ m zo ⁽ a , ^h ) ⁺ m zo ^{( A} , ^H )) ^-

• - 7,968 49 1 b^нгоУ_ь I h нго ( m_Z o ( A , H ) + m_m ( a , h )) + V а

• +, 870,,96 fbнго/, I hн2го (mzo (A, H) + mzo (a, h)) -
• V / Uа 7

• - 917,071 | ^b нго/ h нго I ( m zo ( A , H ) + V а 7

+ m zo ( a , h )) + m zo ( A , H ) + m_Z o ( a , h );

- безразмерная координата аэродинамического фокуса:

x_F ( a , h ) = 0,,33 457 ^b нго / ( x_F o ( A , H ) +

+ Xfo ( a , h )) - ,, 824 72 L нго ( Xf₀ ( A , H ) + Xf₀ ( a , h )) + + 0,052 378 ан_ГО ( Xfo ( A , H ) + Xfo ( a , h )) + + 69,, 349 9 h нго ( Xfo ( A , H ) + Xfo ( a , h )) -

- 0,668 96 ^b нго / L нго ( Xfo ( A , H ) + Xfo ( a , h )) -- 0,0H 42 ^bну / а а нго ( Xfo ( A , H ) + Xfo ( a , h )) -- ,953,9 ^{b н} гу h нго ( Xfo ( A , H ) + Xfo ( a , h )) -- 0,058 39 L н ^а _гоа( Xfo ( A , H ) + Xfo ( a , h )) -

- ,5,320 6 L нго h нго ( Xfo ( A , H )0 Xfo ( a , h )) -

- 0,678 35 а нго h нго ( Xfo ( A , H ) + Xfo ( a , h )) -

- ,,032 4 f ^b нгу а^ 7 ( Xfo ( A , H ) + Xfo ( a , h )) + + 0,225 833 L/ ( Xfo ( A , H ) + Xfo ( a , h )) -

- 0,002 79 а 2го ( Xfo ( A , H ) + Xfo ( a , h )) -

- ,6 233 h н²_го ( Xfo ( a , h ) + Xfo ( A , H )) + ²

+ ,344,992 | ^bнго/ I h нго ( Xfo ( A , H ) + Xfo ( a , h )) +

V / иа 7

+ 49 9,4,45 1 ^bну I h н²_го ( Xfo ( A , H ) + Xfo ( a , h )) -

V / ^U а 7

• - 35 393,4 1 ^bнго/ h нго I ( Xfo ( A , H ) +

V / ^u а    7

+ Xfo ( a , h )) + Xfo ( A , H ) + Xfo ( a , h ).

Аналогичные выражения для коэффициентов можно получить для «самолетной» компоновки:

• -    коэффициент подъемной силы:

C y ( a , h ) = - 3,557 14 ^Ъ ^ ( C yo ( A , H ) +

+ C yo ( a , h )) - 0,10539 L _Г о ( C yo ( A , H ) + C yo ( a , h )) + + 0,0317 77а_го ( C yo ( A , H ) + C yo ( a , h )) + + 3,714 205 h го ( C yo ( A , H ) + C yo ( a , h )) + + 0,211581 b^го/_ь L го ( C yo ( A , H ) + C yo ( a , h )) - а

• - 0,069 7 bу а го ( C yo ( A , H ) + C yo ( a , h )) — а

• - 20,5891 bh го ( C yo ( A , H ) + C yo ( a , h )) + + 0,024 938 L „К ( C yo ( A , H ) + C yo ( a , h )) -- 0,039 66 L го h го ( C yo ( A , H ) + C yo ( a , h )) + + 0,004 564а_го h го ( . C yo ( A , H ) + C yo ( a , h )) + + 5,217 594 f b ^) ( C yo ( A , H ) + C yo ( a , h )) -

  • - 0,000 21 L Го ( C_yo ( A , H ) + C yo ( a , h )) -- 0,005 44 а 2о ( C yo ( A , H ) + C yo ( a , h )) + + 4,231439 h 2 ( C yo ( a , h ) + C yo ( A , H )) +

+ 26,3 94 42 ^f b^г о/ ] h го ( C yo ( A , H ) + C yo ( a , h )) -V    ^U a У

• - 21,8727 ^f| h 2 ( C yo ( A , H ) + C yo ( a , h )) +

V / u а У          2

+269 207 4 f Ъ^hго У (Cyo (A, H) + +Cyo (a, h)) + Cyo (A, H) + Cyo (a, h); - коэффициент продольного момента mz (a, h) = 12,573 06b^ (mzo (A, H) +

⁺ m zo ⁽ a , ^h )) ^{- 0,571 58 L} го ⁽ m zo ^{( A} , ^H ) ⁺ m zo ⁽ a , ^h )) ^-

• - 0,599 96а_го ( m_m ( A , H ) + m_zo ( a , h )) + + 6,889 258 h _ro ( m_M ( A , H ) + m_Z o ( a , h )) -

• - 1,466 7 b^го/ L го ( m zo ( A , H ) + m_Z o ( a , h )) +

+ 1,225 05 b^го/_ь а го ( m_Z o ( A , H ) + m_zo ( a , h )) +

+ 24,000 64 bh го ( m zo ( A , H ) + C yo ( a , h )) -- 0,217 31 L го а ^а го ( m zo ( A , H ) + m_m ( a , h )) + + 0,105 018 L го h го ( m_Z o ( A , H ) + m_zo ( a , h )) + + 0,487 911a_ro h го ( m_Z o ( A , H ) + m_zo ( a , h )) -- 29,632 5 V b^го/_Ъа У ( m zo ( A , H ) + m_Z o ( a , h )) -

• - 0,073 76 L Го ^а ( m_Z o ( A , H ) + m_m ( a , h )) -

• - 0,061 41аУ ( m_Z o ( A , H ) + m_Z o ( a , h )) + + 1,198171 h^ m_zo ( a , h ) + m_zo ( A , H )) -

• -77,328 fbг°/ ) hго (mZo (A, H) + mzo (a, h)) + V   ^а

+ 30,876 79 ^f b^го/_ь ) h го ( m zo ( A , H ) + m_m ( a , h )) -V    ^а

• - 69,817 9 f b^го/_ьк го У ( m_Z o ( A , H ) + ⁺ m zo ⁽ a , ^h )) ⁺ m zo ^{( A} , ^H ) ⁺ m zo ⁽ a , ^h );

• - безразмерная координата аэродинамического фокуса Xf ( a , h ) = 48,172 7 b^г2Ь ( Xfo ( a , h ) - Xfo ( A , H )) +

+ 4,749 686 L го ( Xfo ( a , h ) - Xf₀ ( A , H )) -- 1,687 21 « го ( Xfo ( a , h ) - Xfo ( A , H )) + + 48,898 69 й ^о ( Xfo ( A , H ) - Xfo ( a , h )) -

• - 8,080 47 b ^го/ L го ( Xfo ( A , H ) - Xf_o ( a , h )) +

  + 4,0373 46 b^го/_ь а го ( Xfo ( A , H ) - Xfo ( a , h )) -- 97,113 b^го/_Ьа h го ( Xfo ( A , H ) - Xfo ( a , h )) -^{- 0, 548 27 L} _гоо ^а го ^{( X} Fo ^{( A} , ^H ) ^{- X} Fo ⁽ a , ^h )) ⁺ + 2,689 857 L_roh го ( Xfo ( A , H ) - Xfo ( a , h )) +

  
  

+ 2,099 685a_ro h го ( Xf_O ( A , H ) - Xfo ( a , h )) -

- 77,1818 l b^го/_ь I ( Xfo ( A , H ) - Xfo ( a , h )) +

V / ^а У

+ 0,290 628 L Го ( Xfo ( A , H ) - Xf₀ ( a , h )) -

- 0,04115 а 2о ( Xfo ( A , H ) - Xfo ( a , h )) +

+ 27,425 76 h го ( Xfo ( a , h ) - Xfo ( A , H )) +

+ 30,078 05 1 bу I h го ( Xfo ( A , H ) - Xfo ( a , h )) -

V    ^а

• - 45,063 5 1 b^го/ I h го ( Xfo ( A , H ) - Xfo ( a , h )) -V / ^ а У

• -26,428 4lbу hго I (Xfo(A,H)-
• V   иа

  -Xfo (a, h)) - Xfo (A, H) + Xfo (a, h).

Функциональные зависимости коэффициентов для компоновки «гибрид:

- коэффициент подъемной силы

C y ( a , h ) = 0,085 203 L _то ( C yo ( а , h ) + С у ₀ „о ( А , Н )) + + 2,884 814 h _пго ( C yo _пго ( A , H ) + C yo ( a , h )) + + 4,172 279 b -^ ( C yo _П го ( A , H ) + C yo ( a , h )) -- 0,190132 L го ^a C yo пго ( A , H ) + C yo ( a , h )) -- 3,943 717 b п^о/у пго ( C yo пго ( А , Н ) + + C yo ( a , h )) - 0,188 437 L пго h_tK0C_{y0 т}о ( А , Н ) -- 0,03153 а пго h пго С уо пго ( А , Н ) -- 2,246 337 ^Ъг о/_ь к „о C yo „о ( А , Н ) -- 5,074 07 L го А ^о C yo _то ( А , Н ) -- 6,054128 h пго а го C yo пго ( А , Н ) -- 0,428 328 ^ЪГо/_bL го с уо _то ( А , Н ) -- 0,202132 ^Ъу а го С уо пго ( А , Н ) + а ₂ + 0,379157 f ^{Ъ п}r°/ Ъ а y C yoпго ( А , Н ) + + 50,755 22 h пго C yo ^о ( a , h ) -- 6,561358 ^{f Ъго}/, I С уо пго ( А , Н );

V / ^а У

- коэффициент продольного момента mz (a, h) = 19,349 56 ЪпгоуЪ)а mz „о (A, H) + +1,728 9121пго mz п,о (A, H) +

+ 21,344 88 h пго m z _шо ( A , H ) -

• - 32,250 92 ^{Ъ г}У _a m_{z т}о ( A , H ) + + 2,127166 1 m zпго ( A , H ) + + 34,5418 9 ^Ъпго/ _Ъа h ^о m z „о ( A , H ) -

• - 9,398 498( ^Ъ^ya )( ^Ъго/_Ьа ) m_z пго ( A , H ) + + 15,04179 1„о h то m z пго ( A , H ) + + 7,277154а_т о h m_z пго ( A , H ) -

• - 15,966 96 h _ ( ^Ъу_а ) m_z _ ( A , H ) + + 26,84816 h _ l го m_z то ( A , H );

  - безразмерная координата аэродинамического фокуса

Xf ( a , h ) = - 300,272 3 h ^о ( Xf ( a , h ) +

+ Xf пго ( A , H ) + Xf го ( A , H )) - 16,853 88 ^bго/_bа ( Xf ( a , h ) +

+ х ,пго ( A , H ) + x, го ( A , H )) + + 0,472105 1_TO ( Xf ( a , h ) + x, , ( A , H ) + + Xf to ( A , H )) - 2,39015 b^nT0_//a 1 _ ( Xf ( a , h ) + + Xf пт/ ( A , H ) + Xf _ro ( A , H )) + b

+ 15,229 53 ^ h пт/ ( Xf ( a , h ) + x, „_го ( A , H ) + + Xf to ( A , H )) - 31,019 59а_шоh пт/ ( Xf ( a , h ) +

+ Xf „to ( A , H ) + Xf г/ ( A , H )) -- 4,730 539 h пт/ byba ( Xf ( a , h ) + x, „„( A , H ) + + Xf to ( A , H )) + 200,789 h пт/ 1 т/ ( Xf ( a , h ) +

+ Xf „to ( A , H ) + Xf _ro ( A , H )) + + 32,730 4 h „T/ а т/ ( x, ( a , h ) + x, „to ( A , H ) + + Xf / ( A , H )) + 1,263 621 b^a а т/ ( Xf ( a , h ) + + Xf „to ( A , H ) + Xf „ ( A , H )) + + 1,399 461( Xf ( a , h ) + x, „t/ ( A , H ) + + Xf to ( A , H )) - 2,490 428( b^пт//_Ьа )² ( x, ( a , h ) +

+ Xf „to ( A , H ) + Xf _r0 ( A , H )) -- 2 077,063( h пт/ )² ( x, ( a , h ) + x, _ ( A , H ) + + x, to ( A , H )) + 32,648 05( b^T0/b _a )² ( x, ( a , h ) + + x, „t/ ( A , H ) + x, _Г / ( A , H )).

Вышеприведенные формулы учитывают значения коэффициентов изолированных несущих поверхностей. Рассмотрим зависимости, приведенные для изолированных крыльев различной формы в работе [4]:

• -    для треугольного крыла с утлом поперечного V < 0: с у = 0,264 а - 1,204 4 а h - 0,01197 а ² + 0,119 57 а ² h + + 2,715 а h ² - 0,212 3 а ² h ² - 0,003 69 а ³ - 0,003 41 а ³ h -- 2,633 4 а h ³ + 0,018 а ³ h ² + 0,0911 а ² h ³ - 0,007 4 а ³ h ³ + + 0,000 55 а ⁴ - 0,000 82 а ⁴ h + 0,943 9 а h ⁴;

m z = - 0,066 8 а + 0,304 2 а h + 0,00197 а ² - 0,019 а ² h - 0,703 9 а h ² + 0,033 7 а ² h ² + 0,000 617 а ³ + 0,000 43 а ³ h + + 0,707 2 а h ³ - 0,002 7 а ³ h ² - 0,014 4 а ² h ³ + 0,0011 а ³ h ³ -- 8,873 • 10 5 а ⁴ + 0,00013 а ⁴ h - 0,260 6 а h ⁴;

• -    для плоского крыла прямоугольной формы в плане малото удлинения:

с у = 0,243 5 а - 1,226 6 а h - 0,003 3 а ² + 0,0721 а ² h + + 2,843 3 а h ² - 0,134 4 а ² h ² - 0,004 5 а ³ + 0,002 35 а ³ h -- 2,849 а h ³ + 0,008 3 а ³ h ² + 0,050 7 а ² h ³ - 0,002 27 а ³ h ³ + + 0,000 54 а ⁴ - 0,000 84 а ⁴ h + 1,054 76 а h ⁴; m_z =- 0,070 6 а + 0,378 7 а h - 0,000 95 а ² -

• - 0,006 5 а ² h - 0,908 3 а h ² + 0,0141 а ² h ² + 0,00125 а ³ -- 0,00192 а ³ h + 0,9451 а h ³ + 0,000 367 а ³ h ² - 0,002 7 а ² h ³ -- 0,000 7 а ³ h ³ - 0,000 12 а ⁴ + 0,000 2 а ⁴ h - 0,3 60 7 а h ⁴;

• -    для треугольного крыла малого удлинения с утлом поперечного V > 0:

с у = 0,127 8 а - 0,520 8 а h - 0,005 а ² + 0,048 8 а ² h + + 1,149 9 а h ² - 0,086 2 а ² h ² - 0,001 44 а ³ -- 0,00147 а ³ h - 1,102 6 а h ³ + 0,007 3 а ³ h ² + + 0,037 а ² h ³ - 0,003 05 а ³ h ³ + 0,000 22 а⁴ -- 0,000 32 а ⁴ h + 0,3914 а h ⁴;

m z =- 0,029 9 а + 0,125 а h + 0,000 83 а ² -- 0,007 3 а ² h - 0,282 6 а h ² + 0,012 7 а ² h ² + + 0,00019 а ³ + 0,000 24 а ³ h + 0,280 а h ³ -- 0,001 07 а ³ h ² - 0,005 5 а ² h ³ + 0,000 46 а ³ h ³ -- 2,953 • 10 5 а ⁴ + 4,33 • 10 ^{- 5} а ⁴ h - 0,102 а h ⁴. Данные формулы позволяют перейти от компоновки с прямоугольными несущими поверхностями к крыльям различной формы в плане.

Коэффициент сопротивления аппарата составляет сх = с +с xoa x^xi, тогда зависимость индуктивного сопротивления от подъемной силы крыла можно представить формулой

^C xl =^-| T^ T V 1 w y ⁽ z ^)Г “ ⁽ z ) dz .

• ^{2 (} c y ) ¹

Теперь перейдем к массовой целевой функции. Взлетная масса экраноплана имеет вид [1]

m 0

m H ⁺ m сл

1 - т к - т тс - т су - m /6

где относительная масса крыла находится по уравнению [5]

ткр = 1,15-W-4 • kмех • kК/„ • k„т -ф-np х VS

6- c o ■ cos ¹-⁵ х

ц + 4 Л

•--------------"I 1

П + 1 ^

—

Ц-1 \ п + 3 J ^;

относительная масса фюзеляжа [5]: тф = 1,14kдВ (1 + 0,4ркэаб) (D -Х)ф5 т-3/4, относительная масса оперения [5]:

т о„ = k ^l k ^( 4,4 + 0,8 - 10 -³ • m o ) S_O n ;

m 0

относительная масса шасси (при колесном) [5]:

т ш = kмт k/бт (6 Hш, +11,3)^10-3 + 0,0625k„н рИ^™^- + 0,005.

^{1 +} Р пн.гл

Для шасси на воздушной подушке массу можно определить согласно работе [6]. Относительная масса силовой установки для ТВД имеет вид [5]

^т су = ^1,36 • ^k су •Y дв • N o , k су = 1,1 + (1,36/ у _Д в )(0,1 + 0,9/ N O / ³).

Относительная масса оборудования управления для пассажирского варианта рассчитывается по формуле [5]: ^т /6. упр = ---- ^{+ 0,2 т} цн V^{1 + 0,1} L _р / Г рейс ) ^{+ 0,0} 8.

^т о

Относительная масса топлива для экраноплана с поршневыми двигателями или турбовинтовыми [5]:

— I V • t c I ,    1

т_Т «--- e—     +--

^Т I 270 ц^ K) „    75 K_max

V           * в       / крейс            ^max

I

-е -----нз I     + 0,006.

Ц„

¹ в     Кт max

Характеристики силовой установки. Потребная тяга (мощность) и число двигателей для взлетного режима можно оценить по следующим зависимостям [8], при единой силовой установке:

TV = — P^■ Р = I j^ + — \т 2-

N дв                 ^; п I                I ^ o g ^;

КдвРдв        k g Кг J при раздельной силовой установке, число маршевых двигателей составляет [8]

-ХТ м =        пол g    .

дв "(Ккр • Рдв,)’ число стартовых двигателей рассчитывается по выражению [8]

N ст = ---1--- дв КстРст двдв

jk₊ _L L р- _^мк^мр"

^{1 т}о^д    V дв^дв¹ дв

. g K г J

;

для крейсерского режима полета потребная тяговоору-женность имеет вид

Р ^s =1/К кр        ' кр .

Технико-экономические показатели экраноплана можно оценить по методике, предложенной в работах [1; 5]. Таким показателем являются приведенные затраты, которые находятся следующим образом:

a пр а + а кап. влож ^;

где себестоимость перевозок составляет [1; 5] 100A a =-------------;

^k ком m н ^V крейс

A = ^А ас ^{+ А} ад ^{+ A} т ос ⁺ a t од ⁺ A топ ⁺ A 3п ⁺ В ап •

Приведенные капиталовложения имеют вид [1; 5]:

₌ 100 -е- ( 1,05 С_с + 1,03 С.п„ . b )

а кап. влож              k V В            "

^k ком m ком ^V рейс ^В год

Введем функциональные ограничения с целью обеспечения безопасности движения для проектируемого аппарата, в качестве которых примем условия статической устойчивости экраноплана [9]:

21( A ) >  X , ( m z < 0);

Xf f^2(А Ft    dc’ 1    <0

> Xfh I I < 0 .

X f 9          у dH у m_z = 0

8=const

Первое ограничение обеспечивает статическую устойчивость аппарата по углу тангажа, второе – по относительной высоте полета.

Основная цель, ради которой создается экраноплан, это высокое аэродинамическое качество, максимальный коэффициент подъемной силы, минимальная взлетная

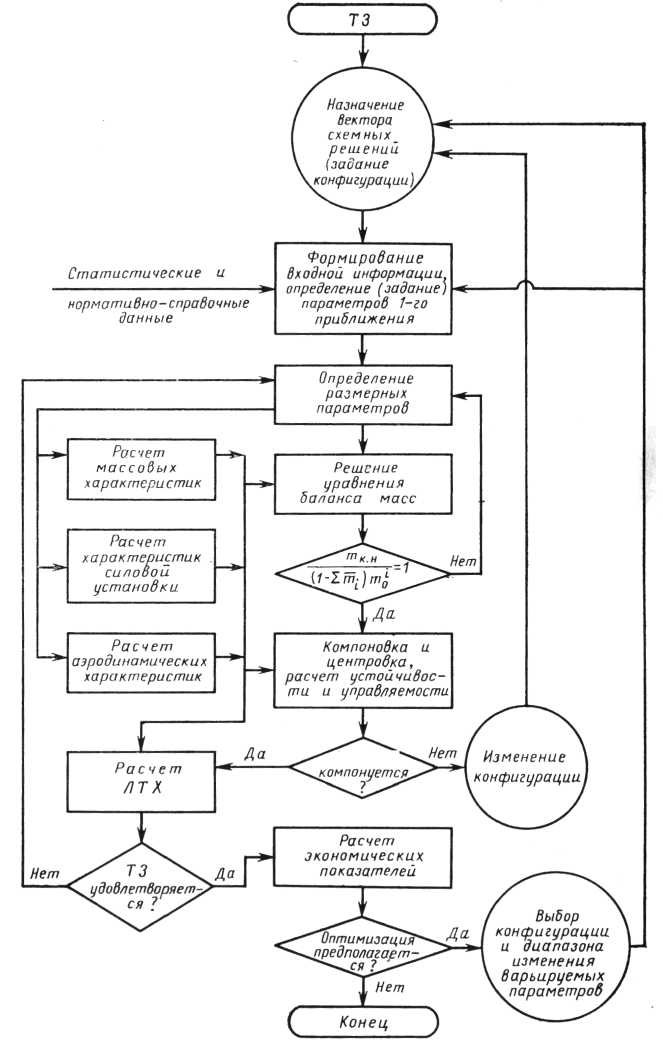
Рис. 2. Блок-схема выбора рациональных параметров экраноплана масса, минимальная тяговооруженность аппарата, минимальные приведенные затраты, тогда нетрудно записать критерии качества:

• -    аэродинамическое качество Ф 1 ( А ) = max( c _y I c x );

• -    коэффициент подъемной силы Ф₂ ( А ) = max( c y );

• -    взлетная масса экраноплана Ф₃ ( А ) = min( m o );

• -    тяговооруженность аппарата Ф 5 ( А ) = min( P_o );

• -    приведенные затраты Ф 6 ( А ) = min( а пр ).

Также могут быть добавлены дополнительные критерии качества, такие как дальность полета, длина разбега и пробега и др.

Допустимое варьирование параметров выбирают на основе статистического анализа существующих конструкций экранопланов. Зондирование пространства параметров можно осуществить любым методом, одним из которых может быть метод квазислучайных последовательностей (ЛП-последовательностей), рассмотренный в работе [10].

Алгоритм выбора рациональных параметров представлен на рис. 2.

Представленная математическая модель позволяет определить параметры экраноплана для различных аэродинамических схем с различными несущими поверхностями; выбрать из ряда проектов решение, наилучшим образом отвечающее поставленным тактико-техническим требованиям и техническому заданию.