Математическая модель задержки на основе СМО с гиперэкспоненциальным и эрланговским распределениями

Настоящая статья посвящена анализу системы массового обслуживания (СМО) H₂/E₂/1 с гиперэкспоненциальным (H₂) и эрланговским (E₂) входными распределениями второго порядка и является продолжением исследований [1–4]. В теории массового обслуживания исследования систем G/G/1 актуальны в связи с тем, что они активно используются в современной теории телетрафика при моделировании систем передачи данных различного назначения, к тому же нельзя получить решения для таких систем в конечном виде для общего случая. Проблему можно было бы решить с помощью законов распределений Вейбулла или Гамма наиболее общего вида, которые обеспечивают диапазон изменения коэффициентов вариаций от 0 до да в зависимости от величины их параметров. Но, как оказалось, преобразование Лапласа функции плотности распределения Вейбулла не может быть выражено в элементарных функциях. Преобразование Лапласа функции плотности гамма-распределения включает параметр а этого закона в показатели степени

+х

Р-а e - stt а-1 e - t/в dt =

Г(а) I в-Ч в

Г ( а ) (в s + 1

а- 1

Г ( а ) =

( в s + 1) ^{а- 1 ,}

и этот закон распределения в теории массового обслуживания можно использовать только в частных случаях при целочисленных значениях а >  2.

В конечном итоге это приводит нас к известному распределению Эрланга.

В качестве основного метода решения задачи использован метод спектрального разложения решения интегрального уравнения Линдли [5; 6], а вспомогательного – приемы аппроксимации законов распределений методом моментов теории вероятностей [7–9]. Вычислительные эксперименты по полученным в работе аналитическим результатам подтверждаются данными имитации [10–12]. Схожие результаты современных исследований по системам массового обслуживания приведены в работах [13–16].

1.    Постановка и решение задачи

В работе ставится задача вывода решения по средней задержке требований в очереди в системе H2/E2/1 с гиперэкспоненциальным и эрлангов-ским входными распределениями второго порядка как основной характеристики любой СМО.

Для системы H2/E2/1 законы распределения интервалов входного потока и времени обслуживания задаются функциями плотности вида

a ( t ) = p X 1 e ^X 1 t + ( 1 - p ) ^ 2 e ^X 2 t ,                        (1)

b ( t ) = 4 ц ² te 2^2ц t .                                             (2)

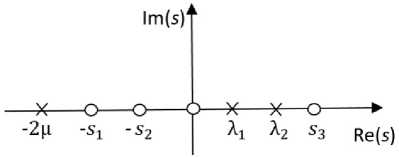
Рис. Нули и полюсы функции ф ( s ) / ф ( s ) для системы H₂/E₂/1

Fig. Zeros and poles of ф+ ( s ) / ф ( s ) function for H 2 /E 2 /1 system

Запишем преобразования Лапласа функций (1) и (2):

A * ( ^s ) = P -^7- ⁺( 1 ^- P ) ^v '     s + X1 ^x '

^X 2

^{s + X} 2

Тогда выражение

*          *

где A ( s ), B ( s ) -

A * ( — s ) B * ( s ) — 1 = ф₊ ( s ) / ф - ( s ) , преобразования Лапласа функ-

ций плотности (1), (2), а ф + ( s ), ф - ( s ) - некоторые дробно-рациональные функции s , для спектрального разложения решения интегрального уравнения Линдли для системы H₂/E₂/1 примет вид: ф±00 =

ф -^{( s} )

= p 7^^

_ ^X 1 - ^s

- 1 =

исключения ошибок построения спектрального разложения. На рисунке полюсы отмечены крестиками, а нули – кружками.

Далее по методике спектрального разложения найдем константу K :

K = lim ^+M = lim ^{( s + s} 1 ^{)( s + s} 2 ¹ = ^ .

I ^s | > 0 ^s |^s | > 0 ( s + 2 ц ) ²         4 ц ²

Построим функцию Ф + ( s ) = K / ф + ( s ), через которую найдем преобразование Лапласа функции плотности задержки:

s ^₂ ( s + 2 ц) 2

^W ( s ) = s ^Ф + ( s ) = 1     „     , •

4 ц ( s + s 1 )( s + s 2 )

Окончательно

- s ( s + s 1 )( s + s 2 )( s - s 3 )

( X ^ - s )( ^ 2 - s )(2 ц + s )

т. к. многочлен 4-й степени в числителе этого вы-

ражения можно представить в виде разложения - s ( s ³ + c 2 s ² + c 1 s + c 0 ) с коэффициентами c 2 = 4 ц--X 1 -X ₂, c 1 = 4 ц ( ц-X 1 -X ₂) + X 1 X 2 , c 0 = 4 ц [ Х 1 Х 2 + + ц ( Х 1 p -X 1 -X ₂ p )]. В свою очередь кубический многочлен s ³ + c 2 s ² + c 1 s + c 0 с такими коэффициентами в стационарном режиме функциониро-

s-.s₉ (s + 2 ц )2

W ( s ) = —--- -1— .                    (4)

4 ц ² ( s + s 1 )( s + s 2 )

Производная от функции W ( s ) со знаком минус в точке s = 0 и даст среднюю задержку требований в очереди:

dW ( s )     = d    s 1 s ₂ ( s + 2 ц ) 2

^ds s        d^s 4 ц ² ( s + s 1 )( s + s 2 )

| s = 0 =

вания СМО при загрузке р = тц / Т х <  1 имеет два действительных отрицательных корня - s 1 , - s 2 и один положительный корень s 3 .

Окончательно

= — +----.

^s 1    ^s 2    ц

Тогда средняя задержка в очереди для системы H2/E2/1 будет равна:

ф₊ ( ^s ) = - s ( s + s 1 )( s + s ₂)( s - s 3 ) ф - ( s ) ( X 1 - s )( X ₂ - s )(2 ц + s ) ²

111 w =—+----, s 1 s 2   ц

Поэтому с учетом специальных условий [5] за

функцию ф + ( s ) примем

ф+ (s) = s (s + s 1)(s + s 2) / (s + 2ц)2, т. к. нули кубического многочлена s = 0, s = -s 1, s = -s2 и полюс s = -2м лежат в области Re(s) < 0, а за функцию

где s ₁ , s ₂ - абсолютные значения отрицательных корней - s ₁ и - s ₂ кубического многочлена s ³ + c 2 s ² + c 1 s + c 0 с приведенными выше коэффициентами. Таким образом, средняя задержка для системы H₂/E₂/1 однозначно определена в виде замкнутой формы (5).

Такой подход к использованию метода спек-

^ф - ( ^s ) = ^{- ( X} 1 ^{- s )( X} 2 ^{- s} )/^{( s - s} 3 )•

На рисунке отображены нули и полюса отношения ф + ( s ) / ф _ ( s ) на комплексной s -плоскости для

трального разложения позволяет определить не только среднюю задержку в очереди из (4), но и моменты высших порядков времени ожидания. Вторая производная от функции (4) при s = 0

Таблица. Результаты экспериментов для СМО H₂/E₂/1 в сравнении с H₂/M/1 Table. Results of experiments for QS H₂/ E₂/1 in comparison with H₂/M/1

Входные параметры Среднее время ожидания р c х для системы H2/E2/1 для системы Н2/M/1 0,1 1 0,083 0,111 2 0,141 0,187 4 0,171 0,230 8 0,182 0,245 0,5 1 0,751 1,000 2 1,764 2,162 4 4,082 4,831 8 8,911 10,402 0,9 1 6,752 9,000 2 20,016 22,409 4 73,321 75,786 8 286,642 289,134 дает второй начальный момент времени ожидания. С учетом определения вариации задержки – джиттера в телекоммуникациях как разброс времени ожидания от его среднего значения [17] тем самым получим возможность определения джит- тера через дисперсию времени ожидания.

Для практического применения расчетной формулы (5) необходимо определить числовые характеристики распределений (1) H2 и (2) E2. Для этого воспользуемся свойством преобразования Лапла- са воспроизведения моментов и запишем началь- ные моменты до третьего порядка для распреде- ления (1):

_{т —} p , ^{( 1} - ^p ) ^х х 1 х ₂ ’

-3 6 p ^{6 ( 1 -} p )

Т —1

х з 3       Л 3

^х 1      ^х 2

_ 2 _ ² P , ^{2 (1} - ^p )

T , х 2         2

х1

.

При аппроксимации с использованием первых двух моментов неизвестные параметры распределения (1) X i , Х 2 , p определяются с помощью следующих выражений [10]:

х1 — 2p / тх, X2 — 2(1 - p) / Тх, p — 2[1 ±V

Отсюда следует, что коэффициент вариации cх > 1. При аппроксимации с использованием первых трех моментов для нахождения параметров распределения (3) необходимо в пакете Mathcad решить систему трех уравнений (6), полученных методом моментов. При этом необходимым и достаточным условием существования решения является выполнение условия: т^Тх -1,5тХ [9].

Для распределения (2) имеем:

1      23              1

^{Тц —}Ц, ^{Тц —}2ц^{2 ,}c^{Ц —} V2.

Таким образом, гиперэкспоненциальный закон распределения второго порядка может определяться полностью двумя первыми моментами и перекрывать весь диапазон изменения коэффициента вариации (1, да). Величины Тх, ТЦ, cх, cц будем считать входными параметрами для расчета среднего времени ожидания для системы H₂/E₂/1 с использованием выражения (5). Тогда алгоритм расчета сведется к последовательному определению параметров распределения (1) из выражений (7) и к нахождению нужных корней многочлена s³+ c2s²+ c 1 s + c0 с приведенными выше коэффициентами, а затем к использованию расчетного выражения (5).

2.    Результаты вычислительных экспериментов

В таблице приведены данные расчетов для системы H₂/E₂/1 для различных случаев нагрузки (малой, средней и высокой) р — 0,1; 0,5; 0,9. Для сравнения в правой колонке приведены данные для близкой системы H₂/M/1, образованной гиперэкспоненциальным (H₂) и экспоненциальным (M) законами распределения. Заметим, что коэффициент вариации для распределения M равен единице, т. е. больше, чем у распределения E₂. Тогда у последней системы средняя задержка будет больше. Коэффициент загрузки в данном случае определяется отношением средних интервалов р — Тц / тх. Расчеты в таблице приведены для удобства для нормированного времени обслуживания ^Тц ^—1.

Заключение

Таким образом, по результатам работы можно сделать следующие выводы.

Научная новизна полученных результатов заключается в том, что получено спектральное разложение решения интегрального уравнения Линдли для рассматриваемой системы и с его помощью выведена расчетная формула для средней задержки требований в очереди для этой системы в замкнутой форме. Данные численных экспериментов подтверждают полную адекватность полученных теоретических результатов, Предложенный подход к анализу систем также позволяет находить джиттер через преобразование Лапласа функции плотности времени ожидания, т. к. он в [17] определен как разброс задержки требований в очереди вокруг среднего значения.

Практическое значение работы заключается в том, что полученные результаты с успехом могут быть применены в современной теории телетрафика, где задержки пакетов входящего трафика играют первостепенную роль. Для этого достаточно знать средние значения интервалов между пакетами входящего трафика и времени обслуживания, что не вызывает трудностей при использовании современных анализаторов трафика.