Математические аспекты архитектурной логики формообразования римского пантеона

ΣΧΟΛΗ Vol. 14. 1 (2020)

Архитектурно-этнографические исследования объектов материальной культуры включают исследование зданий и сооружений, что ставит проблему разработки и апробации методик, основанных на использовании информационных технологий. В настоящей статье на примере форм римского Пантеона апробируется новая методика пропорционального анализа с использованием результатов объемного лазерного сканирования в виде облаков точек.

По периоду античного Рима, не считая трактата Витрувия Десять книг об архитектуре , практически никаких источников о размерах и пропорциях архитектурных сооружений не сохранилось. Тем не менее, объемность трактата Витрувия дает возможность увидеть весьма полную картину профессиональной деятельности архитектора. В частности, можно отметить, что существовало большое количество правил формообразования, выраженных в простейших модульных соотношениях. К сожалению, трактат Витрувия, несмотря на свою емкость, не содержит ни одного случая, когда какое-либо зафиксированное правило можно верифицировать на каком-либо сохранившемся памятнике.

Это привело к появлению большого количества гипотез о правилах формообразования, применяемых античными зодчими. В частности, размерам и пропорциям римского Пантеона посвящено большое количество исследо- ваний. Первые такие исследования были проведены еще в 16–17 веках. В сочинениях Палладио, Серлио, Дегодета, Пиранези, Канины приводятся подробные обмерные чертежи как памятника в целом, так и его деталей. Детальный обзор истории обмеров и создания обмерных чертежей Пантеона приводится в диссертациях М. Сакконе (Saccone 2017) и Л. Альберти (Aliberti 2014).

В 18 веке в работах Блонделя и Эрколани появились первые попытки выявить логику формообразования Пантеона. В 20 веке эта тема получила дальнейшее развитие в работах Г. Д. Грима (1935), Х. Гертмана (Geertman 1980), М. Пелетти (Pelletti 1989), Дж. Сперлинга (Sperling 1998), К. Н. Афанасьева (2000) и других исследователей.

Особый интерес представляет работа Т. Курента (Kurent 1967), в которой обсуждается устройство римских водяных колес, модульная структура которых основана на общепринятом в античном мире приближении отношения длины окружности к диаметру целочисленным соотношением 22/7, впервые полученном в трактате Архимеда Измерение круга . В своей работе, практически не замеченной и никем не цитированной, Курент находит аналогию в пропорциях римского Пантеона. Диаметр купола, равный 43,5 м, он приравнивает 147 футам или 98 локтям (локоть составляет 1½ фута). Соответственно, по пропорции 22/7, длина внутренней поверхности ротонды приравнивается 462 футам или 308 локтям.

Подробная модульно-метрологическая интерпретация форм Пантеона рассматривается М. Джонсом (Jones 2000) в монографии, посвящённой принципам римской архитектуры. Автор работы приводит большое количество, выполненных вручную, измерений элементов Пантеона. Все эти размеры он сопоставляет со справочной величиной римского фута, равного 0,296 м. Большинство сопоставлений дает весьма точное соответствие размеров элементов Пантеона величине римского фута, используемого в качестве модуля.

В работе А. Радзюкевича (2004), независимо от работы Курента, вновь была выдвинута гипотеза о том, что при разметке форм Пантеона использовалась целочисленное отношение 22/7. Эта гипотеза была дополнительно обоснована детальным пропорциональным анализом большого количества элементов Пантеона на основе стандарта римского локтя (0,445 м).

Гипотезы Джонса и Курента–Радзюкевича на первый взгляд очень похожи, так как размеры римского локтя и фута соотносятся в простейшем соотношении 3/2. Тем не менее, в них имеются весьма существенные расхождения в интерпретации пропорций и, соответственно, в реконструкции логики формообразования. Сравнение гипотез представляет собой боль-

А.В. Радзюкевич, Г.Ф. Григоренко /ΣΧΟΛΗ Vol. 14. 1 (2020) 229 шую трудность, так как для уточнения параметров нужны точные размеры элементов памятника.

Работа с «облаками точек»

Такое сопоставление с недавнего времени стало возможным благодаря технологии объемного лазерного сканирования форм памятников архитектуры. Группа ученых из европейских стран в 2005 году с помощью этой технологии провела фиксацию форм римского Пантеона, в результате чего было получено большое количество высокоточных обмеров, зафиксированных в виде масштабных ортофотопланов и облаков точек. Все материалы обмера находятся в открытом доступе: и

Результаты лазерных обмеров Пантеона документированы в двух видах. Во-первых, имеется большое количество растровых изображений разной степени детализации. Все изображения имеют по периметру рамку, которая представляет собой масштабную линейку, по которой можно провести те или иные измерения. Во-вторых, что исключительно важно, имеются непосредственно сами облака точек, которые можно свободно скачать и определить все необходимые расстояния самостоятельно. Специфика работ с облаками точек заключается в том, что поверхности обмеряемого объекта фиксируются в виде большого количества точек, имеющих точные геодезические координаты в пространстве (рис.1).

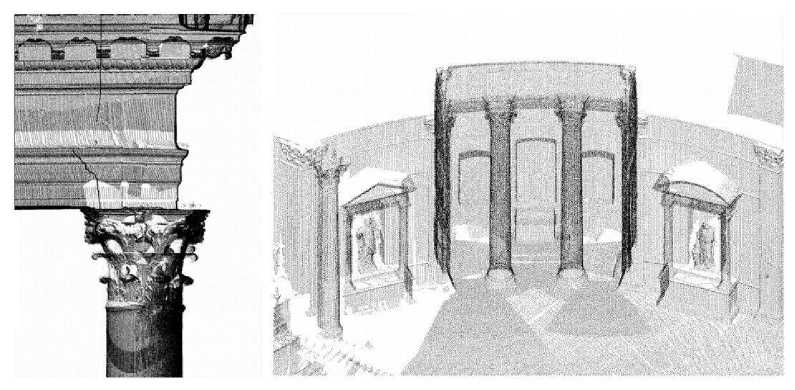
Рис. 1. Облака точек элементов римского Пантеона.

В зависимости от режима сканирования число таких точек может быть разным, но в любом случае, это огромное количество данных. Так, например, полное облако точек внутренней поверхности Пантеона содержит бо- лее 1 600 000 точек. Полное облако точек всех поверхностей Пантеона содержит более 5 000 000 точек. Возникает проблема выработки технологии анализа этого огромного множества данных. Тем более что идеально правильных поверхностей у реальных архитектурных объектов не бывает. Очевидно, что здесь можно произвести практически неограниченное количество измерений. Попытаемся выявить размер внутреннего радиуса ротонды. Теоретически, если определить расстояние от каждой точки стены до определенной вертикальной оси ротонды, то можно вычислить среднее арифметическое значение и принять его за то значение радиуса ротонды, с которым мы будем иметь дело в последующем анализе. Такая технология автоматизированной обработки большого количества данных предусмотрена в программе Leica cyclone, однако мы попробуем сделать это более простым способом. Откроем облако точек в программе AutoCAD и выделим его фрагмент в определённом интервале высот, допустим, в промежутке от 2 до 3 метров от уровня пола. Получаем облако, в котором содержится около 100 000 точек (рис. 2). Если посмотреть на это облако точек сверху, можно увидеть, что линия стен представляет собой множество точек, группируемых внутри полосы, ширина которой колеблется в пределах до 3 см.

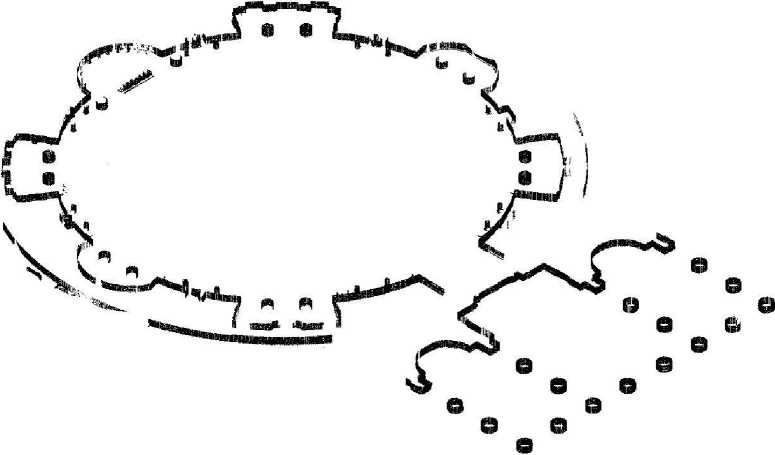
Рис.2. Срез облака точек Пантеона на уровне от 2 до 3 метров от уровня пола.

Реконструкция пропорций ротонды в плане

Попытаемся выявить ключевые размеры ротонды, определяя размер визуально по условной середине таких полос. От геодезической оси ротонды, заданной создателями облака, измерим расстояния до 16 внутренних и 5 внешних характерных точек, находящихся на стенах ротонды (рис. 3). В интерьере Пантеона есть 8 больших и 8 малых ниш, между которыми находится 16 участков стены. Именно эти участки выбраны для измерения. По наружной стене выбраны всего 5 точек по осям ниш в тех местах, где есть данные лазерного сканирования. Измерения внутреннего радиуса ротонды колеблются от 21,76 м до 21,87 м. Измерения внешнего радиуса колеблются от 28,03 м до 28,10 м. Среднее арифметическое значение 16 внутренних радиусов равно 21,82 м и, соответственно, среднее арифметическое значение 5 внешних радиусов равно 28,08 м. Предположим, что проектный замысел ротонды Пантеона действительно был основан на использовании дроби 22/7. Тогда при делении внутреннего радиуса на 7 частей, получаем модуль, равный 3,12 м. Два таких модуля равны 6,24 м, что отличается от полученной толщины стен всего на 2 сантиметра. А девять таких модулей равны 28,08 м, что практически совпадает с вычисленным средним арифметическим внешним радиусом ротонды. Получается, что толщина стены была фактически неким крупным модулем разбивки плана ротонды.

Сравнивая полученные результаты с «ручными» обмерами Джонса, можно убедиться в безусловном удобстве работ с облаками точек. Так, например, внешний диаметр стены ротонды приравнивается Джонсом примерно 55,5 м. Очевидно, что традиционными измерениями провести точное измерение внешней поверхности круглого объекта весьма сложно и трудоемко. Данный «ручной» обмер отличается от лазерного на целых 66 см (56,16 – 55,5 = 0,66). Джонс арифметически приравнивает этот размер 187,5 футам без проведения каких-либо интерпретаций в качестве проектного размера.

Диаметр ротонды по внутренней поверхности стен у Джонса равен 43,57 м, что вполне сопоставимо с полученным нами размером 43,64 м в пределах разброса данных (разница 7 см). Тем не менее, этот размер трактуется Джонсом как «неудобный» размер в 147,2 фута, потому что он использует «справочный» размер фута 0,296 м, никак не увязывая его с размерами реальных объектов. Поэтому, чтобы найти более убедительный проектный размер ротонды, Джонс привязывает его к расстоянию между осями колонн интерьера (44,52 м), трактуя его как 150 футов. И даже при этом он допускает довольно большую погрешность в 12 см:

0,296 × 150 = 44,40, 44,52 – 44,40 = 0,12.

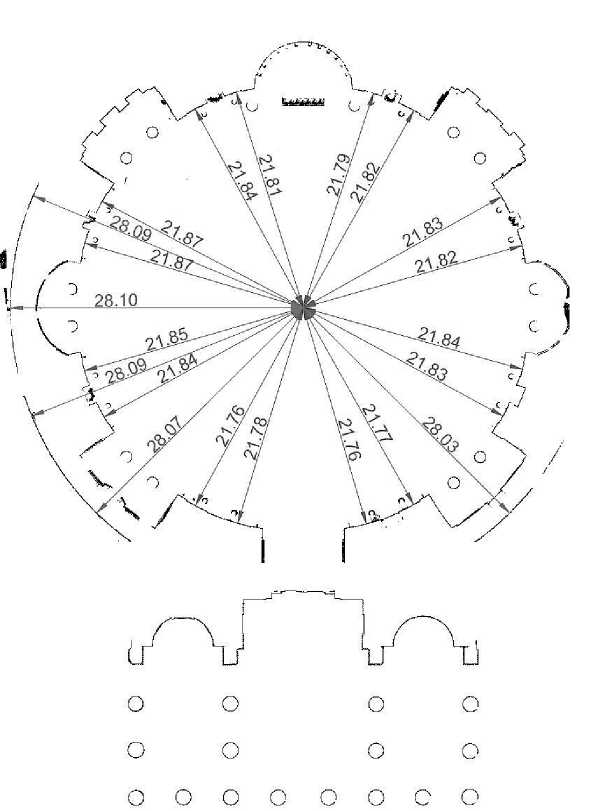
Рис. 3. Размеры радиусов внутренних и внешних стен ротонды римского Пантеона.

В связи с этим, попытаемся вывести размеры римских мер исходя не из метрологических справочников, а из фактических размеров памятника. Приравняем вычисленные выше крупный модуль разбивки плана ротонды, семи римским локтям. Отсюда величина локтя получается равной 44,5 см, а величина фута, соответственно – 29,7 см. Справочная величина фута, используемая М. Джонсом всего на 1 мм меньше вычисленного, однако, при измерении больших размеров, эта разница дает довольно большие отклонения. Сопоставляя вычисленные величины римских мер с фактическими размерами плана ротонды получаем исключительно малые погрешности:

Табл. 1

Анализируемый размер ротонды	Размер по данным лазерного сканирования в метрах	Количе ство больших модулей (3,12 м)	Количе ство римских футов (0,297 м)	Количе ство римских локтей (0,445 м)	Расчетный размер в метрах	По-грешность в метрах
Толщина стен ротонды	6,26	2	21	14	6,24	0,02
Внутренний радиус ротонды	21,82	7	73,5	49	21,80	0,02
Внешний радиус ротонды	28,08	9	94,5	63	28,03	0,05

Помимо исключительной геометрической точности, полученное нами соотношение 9/7 имеет также надежное историческое обоснование – оно полностью соответствует свидетельству Альберти:

Я заметил, что древние в храмах обычно делили лицевую сторону участка на двенадцать частей или – там, где сооружение должно быть очень мощным, – на девять, и из них одну давали толщине стены… (кн. 7, гл. 10).

Можно предположить, что Альберти в этом тексте имел в виду именно ротонду Пантеона. Если внешний диаметр ротонды в 126 локтей поделить на 9 частей, то получим модуль в 14 локтей, что дает основания утверждать, что в Пантеоне было использовано правило с использованием толщины стены в качестве крупного модуля для разбивки ротонды (рис. 4).

Исследование размеров деталей интерьера и кессонов

Учитывая, что внутренний диаметр ротонды равен 98 локтям, по соотношению 22/7, получаем, что длина интерьера равна 308 локтям. Этот размер отлично согласуется с тем, что купол Пантеона делится на 28 кессонов, каждый из которых получается равным 11 локтям (рис. 5).

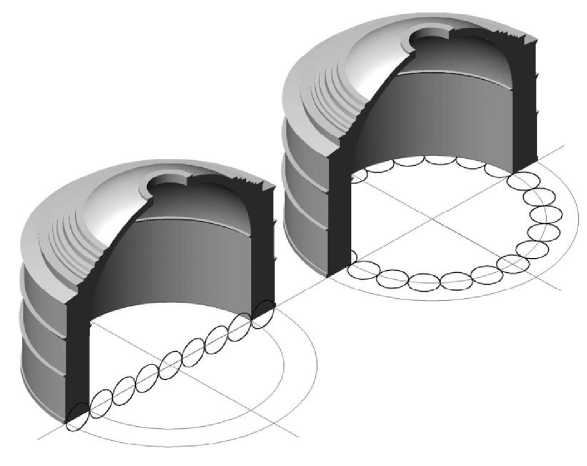
Рис. 4. Реконструкция логики построения формы ротонды.

Модуль – толщина стены, равная 14 римским локтям.

Рис. 5. Реконструкция проектных размеров элементов половины интерьера римского Пантеона

Исследуем элементы интерьера ротонды более детально. В соответствии с гипотезой Курента–Радзюкевича получается, что внутренняя длина стены ротонды равна 308 римским локтям (98 × 22/7). Проверим по облаку точек, могла ли использоваться величина римского локтя в разбивке деталей интерьера. Возьмем фрагмент облака точек ротонды Пантеона в промежутке от 2,3 м до 2,5 м. Разобьем окружность на 308 частей. Теоретически, на линии внутренней стены одна такая часть должна быть равна одному римскому локтю. Посмотрим, как соотносятся этот расчетный модуль с элементами плана. В первую очередь можно заметить, что между осями колонн алтарей достаточно точно вписывается 8 локтей. А от осей этих колонн до осей плоских колонн, обрамляющих алтари, вписывается 7 локтей. В этом случае, ширина алтаря между осями плоских колонн будет равна 22 локтям, что составляет 1/14 окружности интерьера (22 × 14 = 308) (рис. 6).

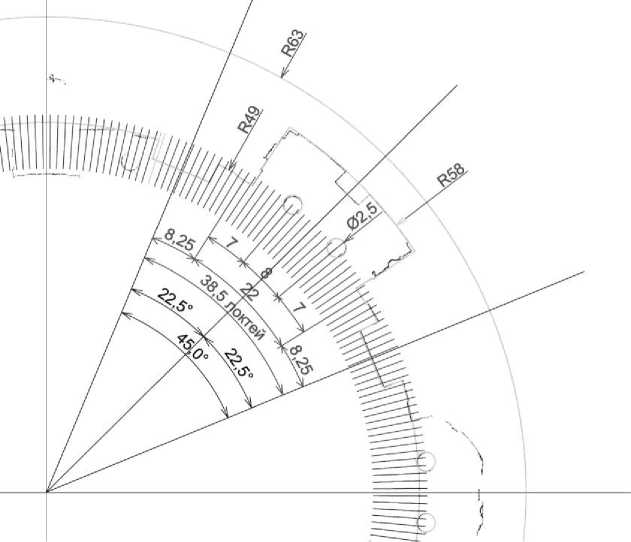
Рис. 6. Анализ размеров интерьера ротонды. Модуль – римский локоть (0,4455 м).

Реконструкция размеров стилобата

Попытаемся определить еще один ключевой проектный размер Пантеона – ширину стилобата (ширину портика по габаритам верхних ступенек). Любопытно, что в имеющихся исследованиях этот размер почти никак не фик- сируется и не интерпретируется. В работе Джонса габаритного размера портика нет, и приводится только размер по осям крайних колонн – 32,03 м, который он интерпретирует как 108 футов (72 локтя). Используя вычисленный выше размер локтя (0,4455 м), получаем, что 72 таких локтя равны 32,08 м. Это больше обмера Джонса на 5 сантиметров (32,03 м) и больше лазерного обмера на 6,5 см (32,015 м). Предположим, что для такого большого габарита это вполне допустимое отклонение.

Попытаемся определить ширину стилобата. По лазерным обмерам этот габарит определить сложно, так как из-за стертости камня он «плавает». По современным фотографиям можно увидеть, что ширина стилобата примерно равна габариту по базам колонн. Однако если посмотреть на чертежи Дегодета, выполненные в 17 веке, то можно заметить, что у ступеней был валик, который выступал за боковую поверхность ступени (рис. 7).

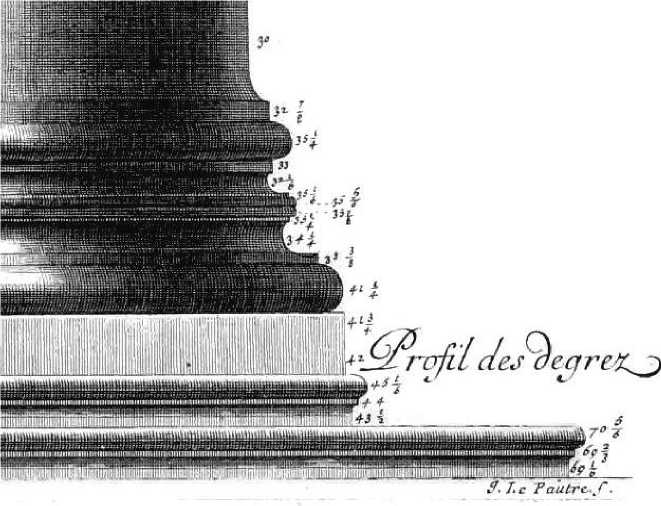
Рис. 7. Фрагмент обмерного чертежа Дегодета.

На современном фото можно увидеть небольшие остатки этих валиков, которые, вероятно, с 17 века почти полностью стёрлись (рис. 8).

Рис. 8. Современное фото боковой поверхности портика Пантеона.

Если изучить чертежи Дегодета, то можно заметить, что он производит измерения, используя величину французского фута и величину малого модуля (парты), который, в соответствии с каноном Палладио, исчисляется как 1/30 нижнего радиуса колонн. На рисунке мы видим, что нижний радиус колонны портика равен 30 таким модулям. Габарит верхней ступени с валиком равен 45 1/6 модулям, что превышает размер радиуса колонны в полтора раза, т.е. равен 2 1/2 римским локтям. Соответственно, получаем, что ширина стилобата получается равной 77 локтям (72 + 2,5 + 2,5).

Можно заметить, что полученный размер ширины стилобата 77 локтей составляет 1/4 от длины окружности ротонды в 308 локтей. Здесь мы видим прямое соответствие между круговым и прямым элементами плана Пантеона. Если опять обратиться к трактату Альберти, то можно найти пример такого «выпрямления» кругового размера. В той же главе Альберти пишет:

«Стену в круглых храмах никто не делал менее, чем в половину, большинство в две трети ширины участка, а некоторые из четырех частей брали три, на высоту которых и возводили внутреннюю стену до уровня свода. Но наиболее опытные зодчие площадь круглого участка делили на четыре части, линию одной из них выпрямляли и по длине ее возводили внутреннюю стену, в отношении одиннадцати к четырем..» (выделено нами).

Здесь у Альберти речь идет об определении высоты внутренней стены круглого храма, однако, важен сам факт использования приема выравнивания «круглого» размера в «прямой». Можно предположить, что данный прием был использован при определении проектного размера ширины портика по габаритам верхних ступеней (рис. 9).

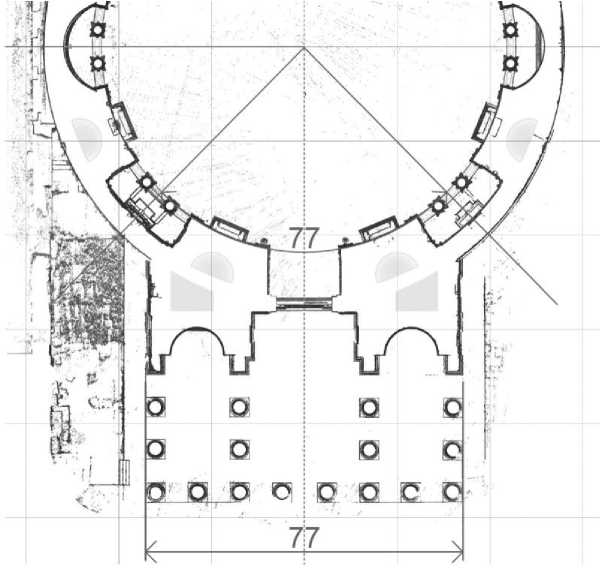
Рис. 9. Преобразование «кругового» размера ротонды в «прямой» размер ширины портика римского Пантеона.

По чертежу Дегодета можно также определить ширину ступеньки портика. Расстояние края валика верхней ступени от оси крайней колонны равно 45 1/6 малых модулей (парт), а тот же размер по второй ступени равен 70 5/6 модулям. Разница составляет 15 4/6 модуля. Если пренебречь величиной в 4/6 модуля, ширина ступени составит 15 модулей, которые равны 1 1/4 фута или. Высота ступеней по обмерам Дегодета равна 6 1/8 модулям. Пренебрегая 1/8 модуля (3,7 мм), получаем высоту ступеней равной 6 модулям, что близко величине в 1/2 фута. Получаем, что ширина и высота ступеней портика Пантеона равны соответственно пяти и двум римским ладоням. В целом, размер портика очень хорошо соотносятся с римскими ладонями (рис. 10).

Детальный анализ размеров элементов портика Пантеона

Используя описанный выше метод определения размеров памятника по облакам точек, можно определить размеры элементов ордера портика Пантеона и, затем, попытаться провести их пропорционально-метрологическую интерпретацию. Результаты этой работы приведены в таблице 2.

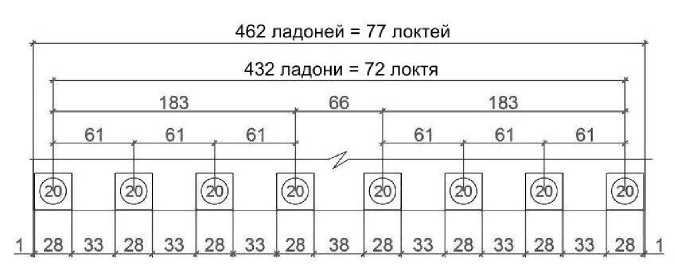
Рис. 10. Реконструкция проектных размеров портика Пантеона. Модуль – римская ладонь (0,0742 м).

Табл.2.

	Элементы портика	Интерпретация размера в римских мерах длины				Средний размер по лазерным обмерам в метрах	Расчетный размер в метрах	По-грешность в метрах
		в локтях (0,445 м)	в футах (0,297 м)	в ладонях (0,074 м)	в дактилях (0,0186 м)
1	База колонн (ширина)	4 2/3	7	28	112	2,07	2,079	-0,009
2	Капитель (высота)	3 3/4	5 5/8	22 1/2	90	1,655	1,671	-0,016
3	Интервал между базами рядовых колонн	5 1/2	8 1/4	33	132	2,46	2,451	+0,009
4	Нижний диаметр колонн	3 1/3	5	20	80	1,48	1,485	-0,005
5	Верхний диаметр колонн	2 11/12	6 3/8	17 1/2	70	1,30	1,2995	+0,0015
6	База колонн (высота)	1 2/3	2 1/2	10	40	0,73	0,7426	-0,0126
7	Фуст колонны (высота)	26 2/3	40	160	640	11,79	11,881	-0,091
8	Полная высота колонны	32 1/12	48 1/8	192 1/2	770	14,20	14,295	-0,095

9	Высота антаблемента с симой	7 1/2	11 1/4	45	180	3,35	3,341	0,09
10	Межосевой размер между рядовыми колоннами	10 1/6	15 1/4	61	244	4,55	4,530	0,02
11	Межосевой размер между центральными колоннами	11	161/2	66	264	4,84	4,91	0,07

В результате сопоставлений фактических размеров с моделью реконструкции погрешности оказались весьма малы. Самая большая погрешность оказалась в размере высоты фустов колонн – 9,1 см. Учитывая большой габарит колонны, можно допустить, что это вполне допустимая погрешность. Но очень вероятно, что наличие такой погрешности связано с тем, что гранитные фусты колонн привозили из далекого египетского карьера в Mons Claudianus, и их размер мог быть изменен в связи с естественными колебаниями эталонов мер. Такие колебания были весьма характерны для античного периода. Так, по исследованиям Дж. Коултона (Coulton 1975), размеры «ионийского» фута в Древней Греции могли колебался в пределах от 0,294 м до 0,296 м.

Реконструкция пропорций портика Пантеона

Полученные результаты оказались весьма близки результатам Джонса. При полном соответствии интерпретации высоты стволов колонн портика, приравненных 40 футам, незначительное расхождение имеется в интерпретации полной высоты колонн. Джонс приравнивает ее 48 футам. В этом случае на суммарную высоту базы и капители остается 8 футов. В работе Джонса размеры этих элементов никак не интерпретируются. Он приводит только обмерные данные в метрах – высота базы колонн и высота капители равны соответственно 0,735 м и 1,64 м. Если же обратиться к лазерным обмерам колонн портика, то можно увидеть, что практически все размеры имеют весьма заметные колебания (рис. 11).

Рис. 11. Обмеры облака точек колонн портика римского Пантеона (размеры в метрах)

Так, например, высота базы колонн колеблется от 0,69 м до 0,78 м. Высота капителей колеблется от 1,60 м до 1,69 м. Предположим, что высота базы колонн равна половине нижнего диаметра колонн. Такое соотношение зафиксировано в трактате Витрувия. Если нижний диаметр колонн интерпретировать как 5 римских футов (80 дактилей), то высота базы должна быть равна 2 1/2 футам (40 дактилей). В этом случае, для того, чтобы «набрать» полную высоту колонны равной 48 футам (768 дактилей), нужно иметь высоту капители равной 5 1/2 футам (88 дактилей). Однако, возможна и иная трактовка этого размера. Его можно определить равным 90 дактилям. Этой, практически неуловимой из-за колебаний размеров разницы в 2 дактиля можно было бы пренебречь, однако она имеет большое значения для реконструкции логики формообразования.

Рассмотрим в этой связи высоту антаблемента. По обмерам Джонса этот размер равен 3,33 м. По нашим измерениям облака точек он равен 3,35 м (размер антаблемента с симой). Это размер весьма близок 7½ римским локтям (180 дактилей). Это ровно в два раза больше высоты капители и, можно предположить, что по проектному замыслу между ними было простое модульное соотношение. И в целом, получается, что все вертикальные размеры ордера кратны 10 дактилям (база колонны 40 – фуст колонны 640 – капитель 90 – антаблемент 180). Полная высота колонны получается равной 770 дактилям или 481/8 футам. На первый взгляд, это не совсем «удобный» проектный размер, однако величина в 770 дактилей очень хорошо соотносится с шириной портика в 77 локтей. Вычисляя соотношение между этими размерами, получаем коэффициент 12/5, который говорит о том, что в осно- ве проектного замысла мог быть использован целочисленный прямоугольный треугольник 5 : 12 : 13. По исследованиям В. Н. Федерякина (1984) и Мар-целло Раньери (Ranieri 2014), использование целочисленных прямоугольных треугольников было весьма распространено в архитектуре Древнего Египта и Древней Греции.

Косвенным подтверждением для данного предположения могут послужить результаты анализа пропорций фронтона портика. Геометрический анализ показывает, что уклон кровли с очень высокой точностью соответствует уклону гипотенузы треугольника «поля фасада» портика (рис. 12).

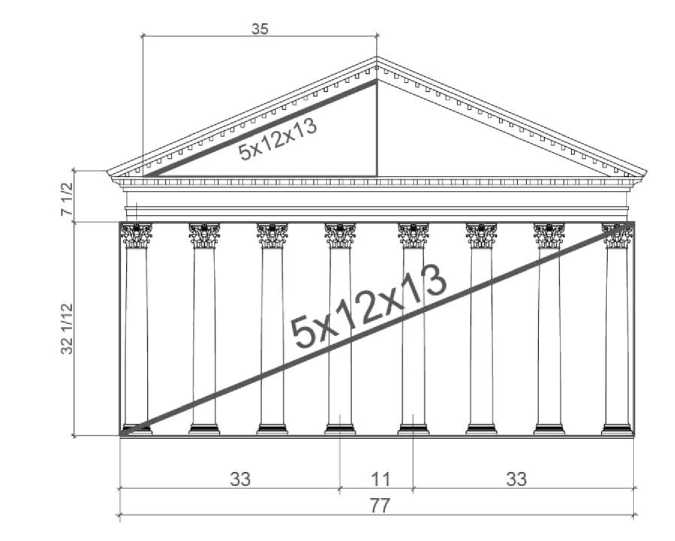
Рис.12. Реконструкция логики формообразования фасада портика Пантеона. Модуль – римский локоть (0,445 м).

С архитектуроведческой точки зрения параллельность угла наклона фронтона и диагонали «поля фасада» представляется важным примером использования принципа подобия. По исследованию Радзюкевича (2004) принцип подобия связывает все ордера Пантеона – портика и больших и малых алтарей интерьера (рис. 13).

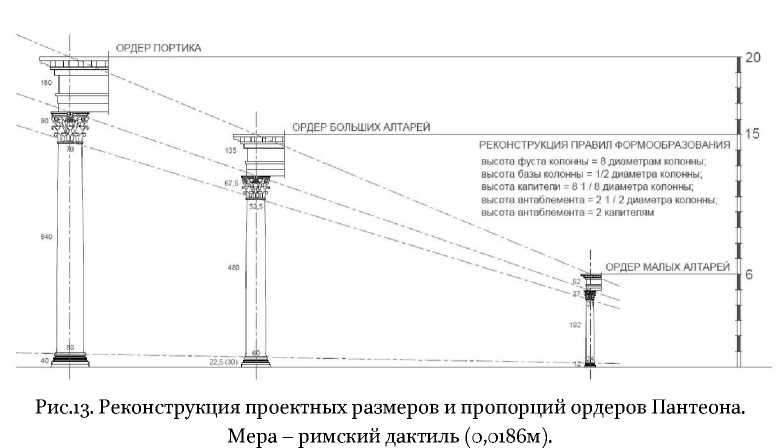
По всей видимости, логика мышления зодчего Пантеона была ориентирована на гармонизацию архитектурных форм на основе использования принципа подобия архитектурных элементов, имеющих разный масштаб. Следует отметить, что такой подход противоречит содержанию трактата Витрувия. В книге третьей, он утверждает, что при изменении высоты ордера, следует менять пропорции архитравных балок и колонн. С увеличением высоты ордера, пропорции архитравных балок, с целью увеличения прочности должны стремиться к «утолщению», а пропорции колонн, для устранения изъяна зрения, возникающего от воздушной перспективы, должны стремиться к форме цилиндра. Можно предположить, что зодчий Пантеона либо не был знаком с трактатом Витрувия, либо трактат в то время не имел того безусловного авторитета, который он приобрел в эпоху Возрождения. Скорее всего, зодчий Пантеона столкнулся с необходимостью использования в одном здании нескольких ордеров, что вынудило его использовать композиционно-художественный прием, основанный на пропорциональном подобии разноразмерных архитектурных элементов.

Выводы

Результаты анализа показали, что в Пантеоне простейшие математические соотношения могли использоваться как инструмент архитектурного формообразования, оказывающий определенное влияние на логику проектного замысла. В частности, использовалась дробь 22/7, позволяющая с высокой точностью производить проектную разбивку круглых элементов ротонды. Мог также использоваться целочисленный прямоугольный треугольник 5 : 12 : 13 для построения прямого угла и для определения основных пропор- ций элементов фасада портика. По всей видимости, в процессе проектирования форм Пантеона использовался прием гармонизации элементов на основе метода подобия с изменением их масштаба.

Реконструкция логики формообразования позволила уточнить не только композиционно-художественные особенности Пантеона, но размеры римских стандартов мер длины, которым производилась разметка форм.

Информационные технологии дают возможность повысить объективность исследования. Очевидно, что их можно эффективно использовать для проведения архитектурно-этнографических изысканий на материале других памятников архитектуры.