Математические методы многокритериального оценивания привлекательности проектов

Управление предприятиями и организациями при помощи проектов – это современный подход в менеджменте, который позволит современным предприятиям эффективно развиваться. На любом предприятии постоянно необходимы инновации: запуск новых изделий в производство, внедрение новых технологий как производственных, так и управленческих. Все это требует разработки и внедрения новых проектов в различных сферах функционирования предприятия.

В результате проектной деятельности предприятия одним из основных этапов является оценка и отбор лучших проектов из имеющихся альтернатив. Целью данной работы является описание математических моделей и способов их реализации для получения интегральных оценок привлекательности проектов, а именно, традиционного метода оценивания и двух оригинальных, основанных на математическом аппарате теории латентных переменных, и теории нечетких множеств. Также задачей данного исследования является анализ полученных оценок и сравнение результатов оценивания с результатами, полученными традиционным методом.

Многокритериальное оценивание проектов

Для оценивания проектов обычно используют многокритериальный подход, когда качество проекта определяется путем сравнения данного проекта с остальными по множеству разработанных критериев.

Выбор критериев обусловлен деятельностью предприятия и типом проекта. Наиболее типичными критериями оценки проектов являются:

• •    новизна и актуальность проекта;

• •    техническая и практическая значимость;

• •    сложность реализации;

• •    инвестиционная привлекательность;

• •    наличие квалифицированных исполнителей проекта;

• •    время реализации проекта;

• •    уровень коммерциализации;

• •    социально-экономическое значение результатов проекта;

• •    потенциал импортозамещения и другие.

Критерии могут быть как количественными, так и качественными. Оценки проектов по количественным критериям выставляются в натуральных шкалах, по качественным критериям оценки получаются на основании экспертного оценивания. По каждому критерию проводится оценивание каждого проекта и на основании частных оценок формируется интегральная оценка каждого проекта.

Рассмотрим некоторые методы получения интегральных оценок привлекательности проектов.

Математическая модель получения интегральных оценок по аддитивному методу

Рассмотрим сначала классический метод оценивания проектов, а потом опишем метод, основанный на латентных переменных, проведем сравнение полученных оценок.

Пусть имеется n проектов П 1 , П 2 , …, П n , которые оцениваются по m критериям K 1 , K 2 , … K m . Обозначим через X ij частную оценку i -го проекта по критерию с K j . Также, в случае разной важности критериев для итоговой оценки проектов, необходимо задать веса критериев w j .

Шкалы измерения проектов по критериям могут быть разного вида: дихотомические, поли-томические, непрерывные интервальные и полуинтервальные. Кроме того, критерии могут иметь разную направленность по степени привлекательности проектов: прямую, когда чем больше оценка по критерию, тем более привлекателен проект, и обратную, когда проекты привлекательнее с меньшей оценкой по критерию. Чтобы адекватно получать интегральные оценки проектов, частные оценки по разным шкалам необходимо нормализовать на единую шкалу.

В качестве процедуры нормализации можно использовать приведение частных оценок на прямую единичную шкалу [1]. Для критериев с прямой шкалой нормализованные частные оценки проектов по критериям x ij можно получить по формуле

Х_ij - min( X_ij )

хij = max(Xij)-min(Xij) , ii а для критериев с обратной шкалой – по формуле xij =

max( X_ij ) - X_ij

max( X_ij ) - min( X_ij ) ii

.

В традиционном подходе интегральная оценка качества проекта проводится по аддитивному методу [1], когда интегральная оценка AP i проекта П i будет определяться как сумма частных оценок, умноженных на веса:

m

Ap_i = ∑ w_jx_ij . j = 1

Перейдем теперь к описанию модели получения интегральных оценок проектов, которая базируется на теории латентных переменных.

Математическая модель получения оценок по методу,основанному на латентных переменных (МЛП)

Данный метод основан на математическом аппарате модели Раша оценки латентных переменных, основанных на методе наименьших квадратов [2–4].

Для использования метода допустим, что интегральная оценка APi проекта является некоторой векторной латентной переменной. МЛП предполагает наличие еще одной векторной латентной переменной AKj, которая характеризует оценочные критерии. Переменные AKj имеют смысл выполнимости или строгости критерия Kj на всем множестве оцениваемых проектов. Чем больше оценка АKj, тем меньше удовлетворяют все проекты в совокупности указанному критерию.

В соответствии с [4] для получения оценок латентных переменных APi и AKj необходимо ре- шать оптимизационную задачу вида nm

Z Z W j • i = 1 j = 1

x j

I

AP - AK. V e i j

AP - ak, + e i j

^ min,

которую можно дополнить условием неотрицательности латентных переменных:

AP > 0; AK , > 0; i = 1,2,.„, n ; j = 1,2,.„, m .                                                      (5)

ij

Метод, основанный на латентных переменных, имеет ряд преимуществ по сравнению с традиционным аддитивным методом. Перечислим основные преимущества этого метода [5].

• 1.    Интегральные оценки проектов являются их уникальными характеристиками и не зависят от множества проектов и набора критериев.

• 2.    Интегральные оценки проектов измеряются по линейной безразмерной шкале, которую можно легко перевести в любую другую, например, вероятностную оценочную шкалу.

• 3.    Кроме интегральных оценок проектов удается получить оценки влияния критериев АK j , которые также линейны. Эти оценки позволяют проводить анализ критериев по различным группам проектов, выделяя наиболее важные из них.

Основным недостатком оценки по МЛП является невозможность аналитического решения задачи нелинейного программирования (4) и (5). Однако ее можно решить численно, например, в табличном процессоре MS Excel с использованием надстройки «Поиск решений».

Далее приведем методику численного решения оптимизационной задачи (4), (5) в среде Excel на некотором примере.

Методика получения численных оценок проектов по МЛП

Приведенный ниже пример (данные сгенерированы случайно) позволит описать методику численного решения оптимизационной задачи, необходимой для получения интегральных оценок проектов по МЛП. Кроме этого, проанализируем полученные результаты и сравним их с оценками, полученными по традиционному аддитивному методу.

Предположим, что имеется 10 проектов, которые оцениваются по 8 критериям. В табл. 1 приведены нормализованные по формулам (1) и (2) на единичную шкалу частные оценки проектов по критериям.

Таблица 1

Частные оценки проектов по критериям для примера

Table 1

Private project evaluations by example criteria

Проект	Критерий
	K 1	K 2	K 3	K 4	K 5	K 6	K 7	K 8
П 1	0,29	0,19	0,22	0,68	0,14	0,38	0,61	0,04
П 2	0,01	0,76	0,09	0,05	0,31	0,41	0,10	0,15
П 3	0,41	0,10	0,55	0,44	0,77	0,31	0,78	0,42
П 4	0,44	0,79	0,80	0,09	0,73	0,87	0,25	0,06
П 5	0,71	0,33	0,34	0,07	0,88	0,94	0,04	0,41
П 6	0,91	0,10	0,52	0,66	0,33	0,45	0,56	0,19
П 7	0,47	0,48	0,99	0,65	0,85	0,54	0,08	0,61
П 8	0,68	0,48	0,94	0,41	0,41	0,23	0,82	0,65
П 9	0,90	0,60	0,16	0,96	0,47	0,38	0,67	0,27
П 10	0,92	0,33	0,18	0,83	0,47	0,25	0,38	0,96
Вес W j	0,61	0,31	0,34	0,88	0,82	0,47	0,98	0,59

На рабочем листе MS EXCEL вводим данные из табл. 1 в диапазон ячеек A2–I14, как это показано на рис. 1. Под латентные переменные APi выделяем диапазон ячеек А17–А26, а под латентные переменные AKj диапазон ячеек B16–I16. В эти ячейки вводим начальное приближение значений переменных, например, в виде нулей. В диапазон В17–I26 вводим формулы, позволяющие рассчитывать слагаемые целевой функции (4). Вводим в В17 формулу =B$14*(B4-EXP($A17-B$16)/(1+EXP($A17-B$16)))^2 и с помощью автоматического заполнения распространяем ее на весь диапазон ячеек. В ячейку Е27 вводим сумму (4) в виде формулы =СУММ(B17:I26). Результат показан на рис. 1.

	A	в	С	D	Е	F	G	н	1
1		Интегральная оценка проектов по МЛП
2		Критерий
3	Проект	К1	К2	КЗ	К4	К5	Кб	К7	К8
4	П1	0,29	0,19	0.22	0,68	0,14	0,38	0,61	0,04
5	П2	0,01	0,76	0.09	0,05	0,31	0,41	0,10	0,15
6	ПЗ	0,41	0,10	0,55	0,44	0,77	0,31	0.78	0,42
7	П4	0,44	0,79	0,80	0,09	0,73	0.87	0.25	0,06
8	П5	0.71	0,33	0,34	0,07	0,88	0,94	0,04	0,41
9	П6	0,91	0,10	0,52	0,66	0,33	0,45	0,56	0,19
10	П7	0.47	0,48	0,99	0,65	0,85	0,54	0,08	0,61
11	П8	0.68	0,48	0,94	0,41	0,41	0,23	0,82	0,65
12	П9	0.90	0,60	0,16	0,96	0.47	0,38	0,67	0,27
13	ШО	0,92	0,33	0,18	0,83	0.47	0.25	0,38	0,96
14	Вес W	0,61	0,31	0,34	0,88	0,82	0,47	0,98	0,59
15		Латентные переменные
16	APi/AKj	0	0	0	0	0	0	0	0
17	0	0,026	0,030	0,027	0,029	0.106	0.006	0,012	0,126
18	0	0,144	0,021	0,055	0,177	0.028	0.003	0,154	0,073
19	0	0,005	0,048	0,001	0,003	0,059	0,018	0,076	0,004
20	0	0,002	0,027	0,030	0,144	0,042	0,063	0,062	0,117
21	0	0,028	0,009	0,009	0,159	0,119	0,092	0,205	0,005
22	0	0,101	0,048	0,000	0,024	0,023	0,001	0,003	0,056
23	0	0,001	0,000	0,079	0,020	0,101	0,001	0.172	0,008
24	0	0,019	0,000	0,065	0,006	0,006	0,033	0.098	0,013
25	0	0,098	0,003	0,038	0,186	0,001	0,007	0.028	0,033
26	0	0,109	0,009	0,034	0,097	0,001	0,028	0,014	0,125
27		Целевая функция (4)			4,032

Рис. 1. Исходные данные в MS Excel для получения оценок по МЛП Fig. 1. Source data in MS Excel for latent variable ratings

Запускаем надстройку «Поиск решений» (Solver), устанавливаем ссылку оптимизации целевой функции на Е27, в качестве изменяемых переменных указываем: $A$17:$A$26; $B$16:$I$16, дополнительные ограничения не вводим, устанавливаем неотрицательность переменных без ограничений. В диапазоне А17–А26 получаем значения латентных переменных AP i , а в диапазоне B16–I16 значения переменных AK j .

Результаты оценивания интегральных показателей привлекательности проектов для данных из табл. 1 представлены в табл. 2.

Таблица 2

Оценки проектов AP i , полученные по данным из табл. 1 разными методами

Table 2

AP i project evaluations obtained from Table 1 using different methods

Проект	П1	П2	П3	П4	П5	П6	П7	П8	П9	П10
Аддитивный метод	1,821	0,959	2,632	2,141	2,161	2,484	2,728	2,869	3,006	2,896
МЛП	0,997	0,001	1,692	1,288	1,307	1,566	1,761	1,898	1,989	1,898

Для сравнения интегральных оценок проектов по традиционному аддитивному методу и МЛП нормируем их так, чтобы сумма оценок всех проектов равнялась единице. Графики нормированных оценок, полученных разными методами, приведены на рис. 2.

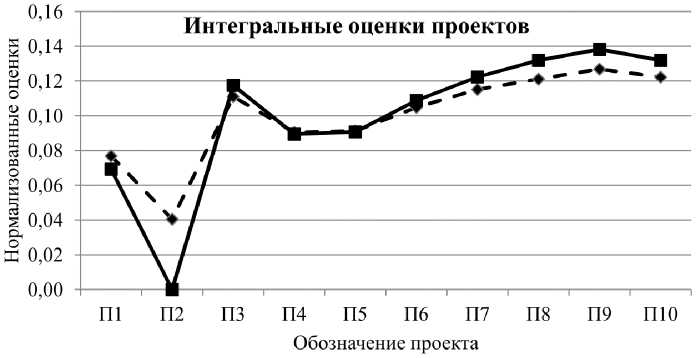
— ♦— Аддитивный метод   ■ МЛН

Рис. 2. Нормированные оценки проектов, полученные по данным из табл. 1 разными методами

Fig. 2. Normalized project estimates obtained from Table 1 using different methods

Из рис. 2 видна высокая согласованность оценок, коэффициент парной корреляции Пирсона для этого примера равен 0,995. Согласованность оценок, полученных по МЛП, с оценками по апробированному аддитивному методу говорит об адекватности оценок, полученных по МЛП.

Математическая модель получения оценок по методу,основанному на нечетких множествах (МНМ)

Данный метод основан на несколько ином подходе многокритериального оценивания проектов. Здесь множество проектов рассматривается как нечеткое с точки зрения привлекательности проектов по каждому критерию. Предполагается, что каждому критерию соответствует некоторый показатель y, индивидуальный для каждого проекта. Каждому показателю критерия Kj будет соответствовать нечеткое множество с функцией принадлежности μj(x). Если для проекта Пi значение этого показателя равно yi, то для частных оценок проектов по критериям можно использовать формулу xij = μj(yi).                                                                                                          (6)

Тогда для оценивания интегральной привлекательности проекта APi можно использовать формулу mm

AP i = X w j x ij = X w j Ц j ( y )• j = 1            j = 1

Рассмотрим основные виды функций принадлежности, которые можно использовать при оценивании для разных видов показателя y . Попробуем рассмотреть основные типы таких критериев и подобрать функции принадлежности для них в общем виде.

Дихотомический показатель – представитель четкого множества, когда проект может либо соответствовать критерию, либо не соответствовать. Функция принадлежности при соответствии признака значению c есть

^{Ц (} y ) * { o.

если проект соответствует критерию;

если проект не соответствует критерию.

Политомический показатель отличается от дихотомического тем, что показатель y может содержать несколько градаций из единичного отрезка, а критерий содержит несколько атрибутов с разными привлекательностями.

Пример такого критерия – «Сложность проекта» (1 – низкая, 0,5 – средняя и 0 – высокая).

Равномерно распределенный показатель в некотором интервале. Критерий выполняется, если показатель y попадает в интервал от а до b . Например, если требуется, чтобы время выполнения проекта было не менее a дней и не более b дней. Функция принадлежности есть

„ ( y ) = (1, при у ^G [ a ; b ^];

‘ ^y) { 0, при y ^ [ a ; b ].

Линейно возрастающий на интервале показатель. Используется, если показатель y был в идеале более b , но не менее а , Например, рентабельность проекта должна быть b рублей и более, если меньше – хуже, но не менее a рублей. Функция принадлежности будет

0, при y <  a ;

y - a

-----, при y e [ a ; b ]; b - a

Ц ( У ) = *

_ 1, при y >  b .

Линейно убывающий на интервале показатель. Аналогичный предыдущему, но для обратных (минимизирующих) критериев с функцией принадлежности вида

1, при y <  a ;

Ц ( У ) = *

b - у          г

-----, при y e [ a ; b ]; b - a

0, при y >  b.

Экспоненциально возрастающий показатель применяется, когда необходимо, чтобы значение y было максимально большим, не менее a. Например, инвестиционная привлекательность проекта должна быть не менее а . Тогда функция принадлежности равна

1    I У - a I Ц( У) = * 1    - expI--I, при y > a;

I a ¹

0, при y <  a .

Экспоненциально убывающий показатель аналогичен предыдущему и применяется, когда необходимо, чтобы значение y было не более b , например, затраты на проект не должны превышать b . Тогда функция принадлежности будет

1        Iy-b I Ц( У) = *

• 1    - exp I       I , при y <  b ;

I Vb 1

0, при y >  b .

Треугольный показатель используется, когда значение y должно быть из интервала от а до b , но наилучшее его значение – в середине интервала. Функция принадлежности равна

|⁽ a + b )/2 ^- y|

Ц ( У ) = *

• 1    - 2^J---------------^L, при y e [ a ; b ]; b ^- a

0, при y ^ [ a ; b ].

Нормально распределенный показатель аналогичен предыдущему, но используется в случае, когда y представляет собой случайную величину, распределенную закону Гаусса. Функция принадлежности будет

Ц ( y ) = exp

( y - ( a + b )/2 ) 2

.

-8-----------5----

( b - a )²

Следует отметить, что для вычисления интегральных показателей привлекательности проектов вместо аддитивного подхода (7) можно использовать подход, основанный на МЛП (4), (5), но с исходными данными, полученными по (6).

Заключение

Таким образом, были рассмотрены некоторые методы.

Аддитивный метод является традиционным, его основным достоинством является простота в вычислительном плане.

Метод, основанный на модели Раша оценки латентных переменных, имеет ряд преимуществ перед аддитивным: линейность полученных оценок, их независимость от множества проектов и набора критериев. Его недостаток – невозможность аналитического решения при практическом применении метода. В работе приведено описание методика получения численного решения в среде MS Excel.

Следует также отметить то, что оценивание на основе теории латентных переменных по модели Раша, основанной на МНК, прошло апробацию и в иных сферах научной и практической деятельности. В частности, по этому методу проводилась оценка объектов недвижимости [6], качества программного обеспечения [7] и профпригодности сотрудников организаций [8].

Метод, основанный на теории нечетких множеств, отличается тем, что множество проектов рассматривается как нечеткое с точки зрения привлекательности проектов по каждому критерию и характеризуется некоторой функцией принадлежности.

Какой метод следует применять при оценивании проектов, зависит от специфики проектов, а также вида критериев и типа оценочных шкал.