Математические методы моделирования поиска принципов действия технических систем

Каждому типу технических задач будет соответствовать определенный запрос к базе данных. Перечислим эти запросы.

• 1    тип. Сформировать множество эффектов, имеющих заданный физический объект и заданный выходной результат. Ключом запроса являются поля записи наименований физического объекта и выходного результат. Запрос покрывает решение таких технических задач, как поиск для некоторой известного технической системы или технологического процесса нового источника сырья или энергии.

• 2    тип. Найти возможные последовательности взаимосвязанных эффектов, преобразующих заданное входное воздействие в заданный выходной результат. Найденная последовательность физического эффекта может служить основой функционирования некоторой технической системы, т. е. представлять собой принцип действия этой системы.

• 3    тип. Сформировать множество эффектов, имеющих заданный физический объект и заданное входное воздействие. Запрос соответствует технической системы, нового ее применения.

• 4    тип. Найти множество эффектов, имеющих заданный выходной результат. Запрос соответствует технической задаче создания устройств для генерирования энергии, получения некоторого вещества, например, излучателя магнитного поля, ультразвука и т. п.

• 5    тип. Сформировать множество эффектов, имеющих заданное входное воздействие. Запрос покрывает решение таких задач, как поиск устройств для поглощения каких-то веществ, энергии, для преобразования или нейтрализации вредных воздействий, для регистрации заданного входного воздействия.

• 6    тип. Сформировать множество эффектов, имеющих заданный физический объект. Данный запрос полезен при решении задач создания устройств для определения создания

каких-то свойств физического объекта, регистрации этих свойств в зависимости от изменения в физическом объекте.

Кроме приведенного набора запросов при решении технических задач проектировщика может интересовать различная информация об отдельном физическом эффекте. Например, «в каких литературных источниках подробно описан данный эффект», «в чем состоит сущность данного эффекта» и т. д. Ключом такого сорта запросов является наименование физического эффекта. Обработка запроса состоит в выдаче содержания соответствующих полей записи физического эффекта. Будем относить все запросы такого вида к запросам 7-го типа.

Отметим, что запросы всех типов могут реализоваться путем обращения к глобальной базе физических эффектов, но для реализации запроса 2-го типа целесообразно сформировать локальную базу в виде графа возможных взаимосвязей эффектов между собой. Создание такой локальной базы дает все преимущества глобальной базы. В дальнейшем рассматривается реализация запроса 2-го типа.

Для получения ответа на запрос 2-го типа достаточным является представление отдельные ФЭ в виде совокупности трех компонент:

W = (1)

где A – входное воздействие; B – физический объект; C – выходной результат, получаемый от действия A на объект B . Отметим, что компоненты A и C задаются как элементы одного словаря фраз естественного языка, что позволяет осуществлять на качественном уровне увязку взаимодействия физических эффектов между собой.

В таблице 1 приведены примеры описаний некоторых физических эффектов по форме (1). Эти описания могут быть получены проекцией трех соответствующих полей из записей физических эффектов в глобальной базе.

Таблица 1

Описание физических эффектов

Table 1

Description of physical effects

Наименование физического эффекта	Входное воздействие	Физический объект	Выходной результат
Пьезоэффект	Деформация	Кристаллы некоторых веществ	Электрическое поле
Эффект Холла	Электрический ток Магнитное поле	Полупроводник	Электрическое поле
Эффект Гаяна	Электрическое поле	Полупроводник	Электрический ток

Отметим, что основой принципа действия технического устройства является последовательность ФЭ из фонда ФЭ:

• < A 1 , B 1 , C 1 >,2, B2, C2>,k, Bk, Ck> (2)

Предполагается совместимость эффектов по входным воздействиям и входным результатам, т. е. входное воздействие последующего физического эффекта совпадает качественно с выходным результатом предыдущего физического эффекта. Это условие можно записать в виде ограничений:

А i+1 = С i , где i = 1, k – 1 (3)

Совместимость физических эффектов здесь предполагается на качественном уровне, т. е. означает совпадение наименований, соответствующих выходных результатов и входных воздействий. Вообще говоря, можно рассматривать более «жесткое» понятие совместимости на количественном уровне, с учетом величин и интервалов значений параметров, которые характеризуют входные воздействия и выходные результаты ФЭ, но это выходит за рамки настоящей работы.

Физический эффект может иметь несколько входных воздействий, наличие которых обязательно для приведения физического эффекта в действие, и несколько выходных результатов. Поэтому в последовательности физических эффектов, представляющей собой физическую основу функционирования технического устройства, необходимо реализовать все входные воздействия каждого физического эффекта. В связи с этим, решение задачи обработки запроса 2-го типа может иметь сложную древовидную структуру.

Задачу обработки запросов 2-го типа можно сформулировать следующим образом. Пусть имеется некоторое множество ФЭ, представленных в форме (1). Этому множеству сопоставим локальную базу данных в виде двудольного графа G = (x ′ , x ′′ , U) , где вершинам множества x ′ соответствует ФЭ, а вершинам на x ′′ – входные воздействия и выходные результаты A, C . Граф G имеет дугу U (x, y) ∈ U, где x ∈ X , y ∈ X , если x соответствует выходному результату эффекта y ; в дугу U (x, y), если x выходному результату эффекта y . Полагаем также, что граф G построен на множестве ФЭ, не имеющем «усилителей», т. е. эффектов, в которых входное воздействие совпадает с выходным результатом.

Предположим, что для каждой вершины x ∈ X на парах дуг ( U, V ) (дуга U входит в x , а дуга V выходит из x ) определены предикаты А_х (U, V ). Полагаем, что если А х (U, V) = 1, то эффект, из которого выходит дуга U, совместим с эффектом, в который входит дуга V , через воздействие X . Если ∆ х (U, V) = 0 , то совместимости между эффектами нет. Тем самым решение вопроса совместимости физических эффектов может быть передано процедуре вычисления предикатов А х (U , V ).. В простейшем случае качественной совместимости предикаты А_х (U, V ). тождественно равны 1. Более сложный случай определения А_х (U , V ). рассмотрен ниже. Отметим только, что чем больше информации привлекается для проверки совместимости ФЭ, тем более «тонким» является определение А_х (U, V )..

Простой путь к графе G :

Х 0 U 1 Х 1 U 2 Х 2 …Х i U i Х i+1 … Х j-1 U j Х j (4)

Будем называть правильным, если для любой вершины! Xj е X ' , входящей в этот путь, выполняется условие стыковки ФЭ, т. е. предикат

∆ х0 (U i , V i+1 ) = 1.

Предположим, что в графе G имеется две поперечные вершины X 0 и Y 0 из X ′′ . Эти вершины играют роль исходных данных для решения задачи обработки запросов 2-го типа. Решением задачи назовем D ( X 0 , Y 0 ) – множество всех простых правильных путей, обладающих следующими свойствами:

• -    хотя бы один правильный путь Ч 0 Г 1 Ч 1 Г 2 Ч 2 …Ч ш Г ш = Н 0 входит в решение;

• -    если вершина x ∈ X ′′ входит в путь, включенный в решение, то для каждой дуги V , входящей в X , в решение включен один из простых правильных путей, начинающийся из вершины X 0 и оканчивающийся дугой V .

Из определения решения D ( X 0 , Y 0 ) следует, что если в графе G сменить ориентацию всех дуг, то его можно рассматривать как И-ИЛИ граф G , где роль И вершин играют вершины из X ′ , а роль ИЛИ вершин – X ′′ .

Таким образом, можно сформулировать следующие задачи:

В графе G по заданным вершинам X 0 , Y 0 найти все решения D ( X 0 , Y 0 ).

Выбрать наиболее эффективное решение из найденного множества решений.

Для решения первой задачи предполагается алгоритм, который строит множество всех решений в виде И-ИЛИ дерева. В корне дерева находится вершина y0. Дерево строится путем просмотра графа G методом «сначала вглубь», начиная с вершины y0, до тех пор, пока всем висячим вершинам не будет соответствовать вершина x, графа G. Вершины дерева, соответствующие вершинам на X′, являются И вершинами, остальные – ИЛИ вершины. Построенное дерево обладает свойством: на любом пути из корня в висячую вершину x0 вершины из множества X′ не встречаются более одного раза. Это означает, что из решений исключены «усилители» длинной более 1, т. е. части цепочек ФЭ, у которых начальное входное воздействие совпадает с конечным выходным результатом.

Алгоритм одновременно вычисляет мощность множества решений. Математическое обоснование правильности работы алгоритма основано на свойствах решений на И-ИЛИ дереве. Ниже приводится описание алгоритма.

Шаг 0. x = y 0 . p = 1 . Обнулить массив Z и включить X в дерево в качестве корня.

Примечание. p – параметр рекурсии; Z[…] – массив счетчиков размерности, равной максимальной длине пути в графе G.

Шаг 1. z[p] = z[p] + 1.

Шаг 2. Если z(p) > a(x) , то перейти к шагу 10. Примечание. a(x) – число дуг, входящих в вершину x

Шаг 3. y = R (x, z[p]) ; включить вершину y в дереве.

Примечание. R(x, i) – процедура выбора вершины y такой, что:

из y в x имеется дуга для вершины x эта дуга имеет среди всех входящих в нее дуг номер i.

Шаг 4. Если вершина y уже встречалась в дереве на пути их корня y 0 в вершину x , то перейти к шагу 7.

Шаг 5. Если x ∈ X ′′ , то перейти к шагу 8.

Шаг 6. Проверить условие стыковки дуг, по которым вошли в x и y . Если условие стыковки выполнено, то перейти к шагу 8.

Шаг 7. Пометить запретом вершину y в дереве и перейти к шагу 1.

Шаг 8. Если y = x 0 , то приписать вершине y в дереве все 1 и перейти к шагу 1.

Шаг 9. x = y, p: = p + 1 , перейти к шагу 1.

Шаг 10. Вычислить β(x) – число запрещенных вершин-преемников вершины x .

Шаг 11. Если x ∈ X ′ , то перейти к шагу 14.

Шаг 12. Если β (x) ≠ α (x), то приписать вершине x в дереве вес, равный сумме незапрещен-ных вершин-преемников x , и перейти к шагу 15.

Шаг 13. Поместить запретом вершину x в дереве и перейти к шагу 15.

Шаг 14. Если β (x) = 0 , то приписать вершине x в дереве вес, равный произведению весов вершин-преемников, и перейти к шагу 15.

Шаг 15. Восстановить по дереву значение x из x , т. е. присвоить x значение вершины – «отца» вершины x .

Шаг 16. Если p = 0 , то перейти к шагу 1.

Шаг 17. Конец.

Примечание. Алгоритм решает первую задачу – строит в виде И-ИЛИ дерева все возможные решения D ( X 0 , Y 0 ). Каждое решение D ( X 0 , Y 0 ) является решением на И-ИЛИ дерева в смысле, определенном в главе 3. Поэтому для решения второй задачи – выбора наиболее эффективного решения из найденного множества, можно воспользоваться методами, которые изложены в [2, 3]. Например, для аддитивных показателей, определенных на каждом физическом эффекте, можно решать задачу поиска решения о минимальном (максимальным) значением показателя: коэффициентов полезного действия преобразования, стоимости реализации принципа действия и т. д.

Выше уже отмечалось, что понятие стыковки физических эффектов можно определять заданием предиката ∆ x (U, V) . Одним из возможных способов является непосредственное определение предиката на каждой паре дуг (U, V) ( U – входит в вершину x ∈ X ′ и V – выходит из нее). Тогда каждой вершине x ∈ X ′′ сопоставляется матрица из нулей и единиц размерностью m x ⋅n x , где m x , n x – число входящих и выходящих дуг вершины x соответственно. Эта матрица определяет предикат ∆ x (U, V) . Достоинством данного способа является его универсальность и высокая трудоемкость получения этих матриц.

Следуя по пути использования более полной информации о физических эффектах для вычисления предиката стыковки, можно предложить другой способ. Будем представлять входное воздействие и выходной результат в описании ФЭ в виде четырех компонент: наименование воздействия, характеристика воздействия, функция, характеристика функции. В этом случае каждой дуге графа G будет соответствовать четырехмерный вектор. Например, эффект Дембера [ n ] можно представить в виде:

( A ¹ , A ², A ³, A ⁴) B ( C ¹ , C ², C ³, C ⁴) (6) где A ¹ – «электромагнитное поле»; A ² – «видимая часть спектра»; A ³ – «увеличение напряженности»; A ⁴ – «монотонное»; C ¹ – «электрическое поле»; C ² – «постоянное»; C ³ – «увеличение напряженности»; C ⁴ – «монотонное»; B – «фотопроводящей высокоомный материал».

Структура описания физического эффекта в виде (6) дает возможность задания нескольких предикатов стыковки физических эффектов и позволяет регулировать жесткость стыковки. Пусть векторы ( A ¹ , A ², A ³, A ⁴) и ( C ¹ , C ², C ³, C ⁴) соответствуют дугам U и V графа G .

Пусть задан вектор δ = ( δ 1 , δ 2 , δ 3 , δ 4 ), где δ i = 0 или 1 при i = 1,4 . Полагаем, что предикат P x ^δi (U, V) = 0 , если Aⁱ ≠ Cⁱ при δ i = 1 ; в остальных случаях P x ^δi (U, V) = 1 . Равенство Aⁱ = Cⁱ означает совпадение соответствующих фраз в словаре.

Определим предикат стыковки следующим образом:

∆ ^δ _x (U, V) = П P_x ^{δ i}(U, V) , i = 1 (7)

В частности, если δ = (1, 0, 0, 0), то предикат ∆δ (U, V) определяет уже упоминавшуюся ранее стыковку по наименованиям входных воздействий и выходных результатов. Отметим, что чем больше единиц содержит вектор δ, тем более «жестким» является условие стыковки ФЭ. Таким образом, определение (7) дает проектировщику возможность варьировать понятием стыковки.

Определение (7) предполагает, что словари воздействий, характеристик воздействий, функций, характеристик функций состоит из отдельных фраз естественного языка. Поэтому сравнение фраз может осуществляться только по равенству. В случае, если эти словари содержат информацию о подчиненности фраз (например, «увеличение» есть частный случай «изменение», то можно построить предикат стыковки, более слабый, чем (7). Для предиката, входящего в выражение (7), положим: P ^{δ i} (U, V) = 0, если δ i = 1, Aⁱ ≠ Cⁱ и Aⁱ не подчинен Cⁱ в словаре; в остальных случаях P ^{δ i} (U, V) = 1.

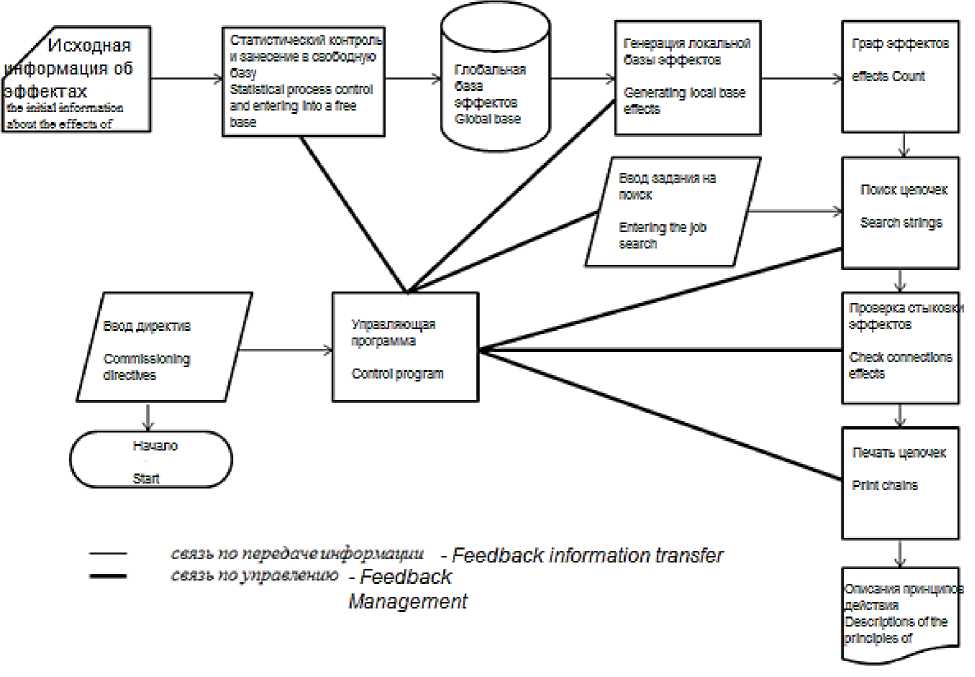
Рисунок 1. Общая схема программы обработки запросов второго типа

Figure 1. General diagram of the processing program of the second type of requests

Заключение

Программная реализация задачи обработки запросов 2-го типа осуществлена на языке СИ. Блок-схема программы приведена на рисунке 1. Управление работой программы осуществляется с помощью директив, которые подготавливаются на перфокартах, либо вводятся непосредственно с терминала. В последнем случае работа происходит в режим диалога. Среди директив имеются директивы ввода ограничения на количество эффектов в последовательности физических эффектов, директива задания предикатов стыковки в виде (7).