Математические методы моделирования в эксперименте по выявлению оптимальных дозировок пробиотика в рационах цыплят-бройлеров

Представляемая вниманию читателя статья посвящена комплексным статистическим исследованиям эмпирических данных по влиянию спорогенного пробиотика «Olin» как фактора, эффективно влияющего на убойные и мясные качества тушек цыплят-бройлеров. Приведена методика и результаты решения с помощью графических и аналитических процедур ранней версии пакета анализа данных SPSS Base 8.0 для Windows ряда связанных между собой задач статистических исследований, начиная от корреляционного и факторного анализа множества исходных показателей убойных и мясных качеств тушек цыплят-бройлеров с целью выявления ведущих информативных показателей и заканчивая оптимизацией дозировки по критериям качества полуфабриката.

В работе [9] рассматривалась роль спорогенного пробиотика «Olin», как фактора, эффективно влияющего на мясные и убойные качества тушек цыплят-бройлеров. Было показано, что его применение в рационах цыплят-бройлеров может служить эффективным способом повышения продуктивности, при дозировке данного пробиотика 1 кг на 1 т комбикорма в течение первых 15 дней выращивания. При этом методической основой выявления эффекта влияния дозировки пробиотика «Olin» в комбикормах являлся традиционно используемый для сравнения средних по вариантам эксперимента t-критерий (критерий Стьюдента), а инструментарием статистической обработки эмпирических данных служила электронная таблица Excel.

Материалы и методы исследований

План описанного в работе [9] эксперимента по исследованию влияния дозировки пробиотика «Olin» в комбикормах на мясные и убойные качества тушек цыплят-бройлеров предусматривал четыре варианта опытов, результаты которых измерялись с шестикратной повторностью, рекомендуемой в сельскохозяйственной практике [3, 6]. Варианты эксперимента предусматривали три дозировки пробиотика «Olin»: 0,015; 0,022 и 0,029 г/гол.; контрольный опыт предполагал основной рацион кормления цыплят-бройлеров без добавки пробиотика. В качестве выходных показателей регистрировались: предубойная масса; масса потрошеной тушки; масса съедобных частей; масса несъедобных частей; масса мышц; масса филе, масса костей. Помимо перечисленных исходных показателей, рассчитывались также аналитические показатели: убойный выход, %, а также отношение съедобных частей к несъедобным.

Такому плану эксперимента отвечают следующие аналитические задачи:

задача 1: по результатам корреляционного и факторного анализа комплекса выходных показателей эксперимента установить латентные факторы и выявить ведущие (информативные) показатели;

задача 2: рассчитать средние значения ведущих выходных показателей и оценить статистическую значимость влияния экспериментальных дозировок пробиотика «Olin», по сравнению с контролем, на информативные показатели;

задача 3: определить спецификацию эконометрических моделей, описывающих зависимость ведущих выходных показателей убойных и мясных ка-а честв тушек цыплят-бройлеров от дозировки пробиотика «Olin» в комбикормах, оценить их параметры и выполнить оптимизацию дозировки по критериям качества полуфабриката.

В принципе, все три задачи могут быть решены и с помощью электронной таблицы Excel , но, как показано нами в публикациях [4, 8, 10, 11], использование в этих целях базового модуля SPSS Base предоставляет значительно более широкие аналитические и графические возможности [2].

Ниже последовательно раскрывается содержание исследований, направленных на решение сформулированных задач.

Результаты исследований

Начальным этапом любых статистических исследований является проверка эмпирических данных на соблюдение условий применения параметрических методов анализа – корреляционного, регрессионного, факторного и других [7, 12, 17]. К этим условиям, прежде всего, относятся однородность и нормальность распределения показателей, включаемых в анализ. Проверка массива эмпирических данных по влиянию спорогенного пробиотика «Olin» на мясные и убойные качества тушек цыплят-бройлеров на нормальность распределения показателей нами проводилась графическими и аналитическими средствами пакета статистических программ SPSS Base [19].

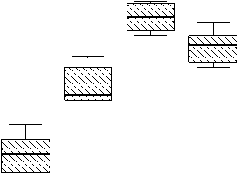
Наиболее наглядным графическим средством проверки исходных показателей на нормальность распределения являются ящичковые (коробчатые) диаграммы, часто называемые также диаграммами Тьюки [1]. Эти диаграммы, иллюстрирующие распределение всех семи исходных показателей по опытам и повторностям, представлены на рисунке 1 а и б , причем для удобства просмотра они разбиты на две подгруппы – с большими и меньшими значениями показателей.

б

Рис. 1 – Распределение масс частей полуфабриката цыплят-бройлеров

Из представленных на этом рисунке диаграмм можно с большой уверенностью сделать вывод о выполнении основного условия корреляционного анализа – однородности исследуемой выборки и нормальности распределений показателей: «выбросы» (экстремальные значения) отсутствуют, медианы всех семи показателей расположены практически посередине «ящичков», отражающих центральную тенденцию распределения масс частей полуфабриката, и симметрично относительно всех 24-х измерений. Проверка по критерию Колмогорова-Смирнова [1]

подтвердила гипотезу нормальности распределений всех введенных в анализ показателей: двусторонняя статистическая значимость параметра отклонения распределений от нормальности составила от 0,994 для массы мышц до 0,721 для предубойной массы, что значительно превосходит критический уровень 0,05.

На следующем этапе статистических исследований проводили множественный корреляционный анализ с помощью процедуры « Correlate » пакета статистических программ SPSS Base – таблица 1.

Таблица 1 – Корреляционная матрица исходных показателей мясных и убойных качеств тушек цыплят-бройлеров

Масса	Статистика	Масса
		предубой-ная	потрошеной тушки	съедобных частей	несъедобных частей	мышц	филе	костей
предубойная	R	1	0,809	0,843	-0,128	0,804	0,804	0,192
	p	,	0,000	0,000	0,550	0,000	0,000	0,369
потрошеной тушки	R	0,809	1	0,771	-0,021	0,801	0,810	0,036
	p	0,000	,	0,000	0,923	0,000	0,000	0,869
съедобных частей	R	0,843	0,771	1	0,188	0,881	0,878	-0,036
	p	0,000	0,000	,	0,380	0,000	0,000	0,869
несъедобных частей	R	-0,128	-0,021	0,188	1	-0,010	0,036	-0,096
	p	0,550	0,923	0,380	,	0,964	0,867	0,657
мышц	R	0,804	0,801	0,881	-0,010	1	0,893	-0,078
	p	0,000	0,000	0,000	0,964	,	0,000	0,718
филе	R	0,804	0,810	0,878	0,036	0,893	1	-0,032
	p	0,000	0,000	0,000	0,867	0,000	,	0,882
костей	R	0,192	0,036	-0,036	-0,096	-0,078	-0,032	1
	p	0,369	0,869	0,869	0,657	0,718	0,882	,

Из таблицы 1 видно, что большая часть выборочных коэффициентов парной корреляции статистически значима на высоком уровне – не хуже 0,0005 (выделены полужирным шрифтом), что, с учетом принципа Бонферрони (ужесточении уровня значимости пропорционально числу рассматриваемых показателей), свидетельствует о наличии сильных связей между большинством показателей мясных и убойных качеств тушек цыплят-бройлеров. Так, с предубойной массой сильно коррелируют такие показатели, как масса потрошеной тущки, масса съедобных частей, масса мышц и масса филе. В противоположность этому, масса несъедобных частей, с одной стороны, и масса костей, с другой, не коррелируют с каким бы то ни было другим исходным показателем. Это позволяет рассчитывать на результативность логически связанной с корреляционным анализом статистической процедуры – факторного анализа.

Следующий этап статистического исследования – факторный анализ, предназначенный для выявления структуры совокупности исходных показателей, а также выделения латентных факторов и их связи с исходными показателями – проводили по методу главных компонент процедуры «Data Reduction» пакета SPSS Base. Данный метод предполагает выполнение определенных математических операций над корреляционной матрицей, в результате которых из совокупности исходных показателей последовательно выделяются так называемые главные компоненты – латентные факторы, общее число которых равно числу анализируемых показателей, но при этом имеется возможность ограничиться меньшим количеством наиболее значимых главных компонент, именуемых главными факторами [16, 18]. Проблема здесь заключается, во-первых, в том, чтобы минимизировать их число, не превысив уровень геометрических искажений, возникающих из-за снижения размерности факторного пространства, и, во-вторых, обеспечить удачную интерпретируемость главных факторов, что достигается путем их вращения по тому или иному алгоритму.

Определение факторной структуры – это не только математическая операция, но и, в определенной мере, искусство аналитика, поэтому остановимся на этом этапе более детально.

Для сокращения последующего изложения введем следующие обозначения:

Х 1 – предубойная масса, г; Х 2 – масса потрошенной тушки, г; Х 3 – масса съедобных частей, г; Х 4 – масса несъедобных частей, г; Х 5 – масса мышц, г; Х 6 – масса филе, г; Х 7 – масса костей, г.

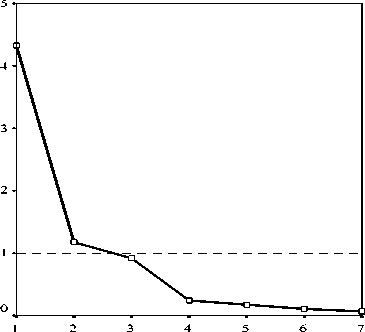
Первый наглядный результат факторного анализа по методу главных компонент, представленный на рисунке 2 а , – график упорядоченных собственных значений корреляционной матрицы ( Scree diagram )», иначе называемый также график «каменистой осыпи».

б

а

Номер компоненты

1,0

,5

0,0

Компонента 1

х4

х7

х3

х65

х2

х1

1,0

Рис. 2 – Результаты факторного анализа: а – график «каменистой осыпи»; б – двухфакторная структура множества показателей мясных и убойных качеств тушек цыплят-бройлеров

По правилу Кайзера, согласно которому главными факторами считаются главные компоненты с собственным значением больше единицы, можно было бы ограничиться двухфакторной моделью структуры множества исходных показателей. Эта модель обладает высокой наглядностью – она представлена на рисунке 2 б в виде плоскости с координатами двух первых главных компонент, на которой «звездочками» обозначены исходные показатели, большинство которых находятся на положительном полюсе первой главной компоненты, и лишь два – масса несъедобных частей (Х4) и масса костей (Х7) – расположены, соответственно, на положительном и отрицательном полюсе второй главной компоненты. Однако при этом геометрические искажения превышают 20%, при рекомендуемом уровне искажений не более 15% [14]. Поэтому в качестве рабочей модели структуры множества исходных показателей принимаем трехфакторную модель, объясняющую около 92% общей дисперсии – таблица 2. Из этой таблицы видно, что, хотя трехфакторная структура множества исходных показателей более точна, уровень геометрических искажений составляет всего 8%, распределение нагрузок на главные факторы нельзя считать оптимальным: третий главный фактор сильно не коррелирует ни с одним показателем (сильные корреляции выделены полужирным шрифтом). Вращение главных факторов по критерию «варимакс» снимает эту проблему.

Таблица 2 – Матрица нагрузок показателей мясных и убойных качеств тушек цыплят-бройлеров на главные факторы

Показатель	Коэффициент корреляции с главной компонентой
	до вращения			после вращения по критерию «варимакс»
	1	2	3	1	2	3
Предубойная масса ( Х 1 )	0,916	-0,240	0,035	0,915	-0,135	0,208
Масса потрошеной тушки ( Х 2 )	0,900	-0,055	-0,021	0,900	-0,043	0,038
Масса съедобных частей ( Х 3 )	0,943	0,163	0,096	0,941	0,196	-0,031
Масса несъедобных частей ( Х 4 )	0,019	0,743	0,665	0,007	0,996	-0,047
Масса мышц ( Х 5 )	0,943	0,062	-0,106	0,945	-0,018	-0,104
Масса филе ( Х 6 )	0,945	0,062	-0,031	0,945	0,034	-0,050
Масса костей ( Х 7 )	0,021	-0,730	0,677	0,005	-0,046	0,995
Объясняемая дисперсия, %	61,7	16,9	13,1	61,7	15,1	15,0

Из матрицы нагрузок исходных показателей мясных и убойных качеств тушек цыплят-бройлеров на главные факторы, полученной в результаты оптимизации факторной структуры по критерию «вари-макс», видно, что первый главный фактор сильнее всего связан с показателями «масса мышц» и «масса филе» (коэффициенты корреляции 0,945), несколько меньше его связь с показателями «масса съедобных частей», «предубойная масса» и «масса потрошеной тушки» (коэффициенты корреляции 0,941; 0,915 и

0,900 соответственно). Он наиболее информативен – объясняет 61,7% суммарной дисперсии. Два другие латентные факторы менее информативны, объясняют по 15% общей дисперсии, при этом второй главный фактор сильно связан с показателем «масса несъедобных частей» (коэффициент корреляции 0,996), третий – с показателем «масса костей» (коэффициент корреляции 0,995).

Таким образом, по результатам выполненного факторного анализа можно уверенно выделить сле- дующие ведущие информативные показатели: масса мышц; масса филе; масса несъедобных частей; масса костей. Эти четыре показателя сильно связаны с главными факторами и могут являться их заменой в дальнейшем анализе. Дополнительную информацию дают

а

2,0

1,0

0,0

-1,0

-2,0

Группа

▲     4

•     3

■      2

О      1

Total Population

Rsq = 0 8928

1000         1100

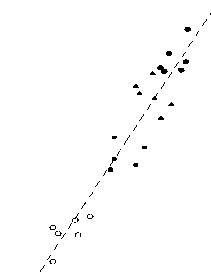
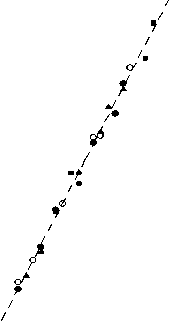
диаграммы рассеяния, иллюстрирующие корреляционные связи выделенных нами по результатам факторного анализа ведущих информативных показателей с главными факторами – рисунок 3.

б

Группа

▲     4

е     3

■      2

о      1

Total Population

Rsq = 0 8932

Масса мышц, г

г

2,0

1,0

0,0

-1,0

-2,0

в

Группа

▲     4

•     3

■      2

О      1

Total Population

Rsq = 0 9928

Масса филе, г

Группа

▲     4

•     3

■      2

О      1

Total Population

Rsq = 0 9895

290     300     310     320

Масса костей, г

290     300     310     320

Масса несъедобных частей, г

Рис. 3 – Корреляция информативных показателей мясных и убойных качеств тушек цыплят-бройлеров с главными факторами

Поясним эти диаграммы. Одним из результатов факторного анализа являются метки главных факторов, соответствующие значениям коррелирующих с ними исходных показателей. Так, на диаграмме рисунка 3 а значениям массы мышц опытных тушек цыплят-бройлеров соответствуют метки первого главного фактора, а так как коэффициент корреляции между массой мышц и первым главным факторов высокий – 0,945, «облако» точек на диаграмме рассеяния образует вытянутое вдоль линии регрессии «веретено». Примечательно, что точки, отвечающие различным опытам, разделены: левее и ниже расположены точки группы 1 (контроль), правее и выше – точки группы 3 (цыплята-бройлеры, в рацион кормления которых был добавлен пробиотик в количестве 0,022 г/гол.).

Качественно такая же картина наблюдается и на диаграмме рисунка 3 б. Это весьма наглядно подтверждает тот факт, что добавка в рацион кормления пробиотика влечет за собой улучшение мясных ка- честв цыплят-бройлеров. В противоположность этому, расположение точек на двух других диаграммах рассеяния эту закономерности не обнаруживают, и на этом основании можно полагать, что ни масса несъедобных частей, ни масса костей не связаны с добавкой пробиотика. Отсюда следует, что в дальнейшем анализе влияния дозировок пробиотика «Olin» на качества тушек цыплят-бройлеров достаточно ограничиться двумя ведущими информативными показателями – массой мышц и массой филе.

Из представленных выше результатов исследований следует, что из исходного множества семи показателей мясных и убойных качеств тушек цыплят-бройлеров в дальнейшем анализе достаточно ограничиться двумя ведущими информативными показателями – массой мышц и массой филе. Именно эти показатели являются индикаторами влияния дозировок пробиотика «Olin» на качества тушек цыплят-бройлеров.

В соответствие с этим выводом, задачей раздела является оценка статистической значимости влияния экспериментальных дозировок пробиотика «Olin», по сравнению с контролем, на эти информативные показатели. Решение данной задачи предполагает реализацию следующих этапов статистических исследований: дисперсионный анализ, цель которого – выявить статистическую значимость различия средних значений индикаторов мясных качеств тушек цыплят-бройлеров по всей совокупности вариантов опытов; применение процедур множественного сравнения средних, а также традиционным методом, основанном на критерии Стьюдента; разбиение вариантов опытов на однородные (статистически неразличимые) группы; сравнение конкурирующих методик анализа результатов эксперимента.

Наше обращение к методам множественного сравнения средних не является случайным. Несмотря на очевидность некорректности использования в этих а целях методов парного сравнения, основанных на критерии Стьюдента (t-критерия), а также на наличие современных информационных технологий, позволяющих проводить множественное сравнение средних практически в «автоматическом режиме», до настоящего времени эти методы еще мало применяются на практике. Опыт, однако, показывает, что замена множественного сравнения результатов эмпирических данных парными сравнениями может привести к неверным выводам: сравнивая в один прием лишь две средние, мы лишаем себя информации об остальных средних, то, что невозможно на двух случайных выборках, может стать вполне возможным на большем их числе (чем больше проводится испытаний, тем более редкие события могут произойти). Кроме того, незначимые различия, накапливаясь от пары к паре, могут стать вполне значимыми, хотя мы этого не замечаем.

б

N =     6        6

N =      6        6

Группа

Группа

N =     6

Группа

N =      6        6        6        6

Группа

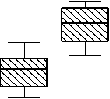
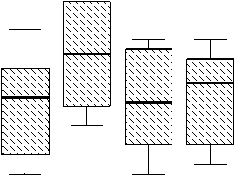
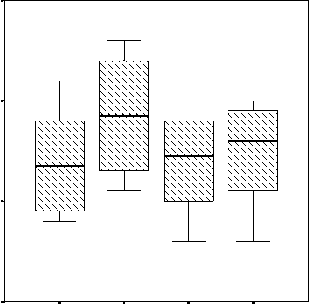
Рис. 4 – Распределение ведущих информативных показателей мясных качеств тушек цыплят-бройлеров: а – масса мышц; б – масса филе; в – масса несъедобных частей; г – масса костей

Сказанное вовсе не означает, что традиционно используемое в практике оценки результатов сельскохозяйственных экспериментов понятие наименьшей существенной разности (НСР) [2, 5, 13] полностью теряет свою значимость. Мы не вполне разделяем точку зрения А.И. Орлова о том, что «высокие статистические технологии» лишают права на использование так называемых «низких» статистических технологий [12]. Во-первых, сравнение средних по критерию наименьшей существенной разности нельзя отне- сти к «низким» статистическим технологиям, это, по терминологии А.И. Орлова – классическая статистическая технология. Во-вторых, логика подсказывает по крайней мере две возможности корректного использования критерия Стьюдента: следует сравнить две ближайшие средние, и если по критерию Стьюдента их разность статистически значима, то значимы будут и разности остальных средних; можно завысить требования к критическому уровню значимости – вместо традиционно принимаемого р-уровня 0,05 принять критический уровень значимости равным 0,05/m, где m – число сравниваемых средних (принцип Бонферрони).

Перейдем теперь непосредственно к сравнению средних по вариантам экспериментов, направленных на выявление роли спорогенного пробиотика «Olin» на мясные и убойные качества тушек.

В соответствие с результатами первой части статистических исследований, достаточно сравнить средние двух ведущих информативных показателей качества тушек – массы мышц и массы филе. Остальные показатели либо коррелируют с этими двумя индикаторами качества полуфабриката, либо не критичны к добавке пробиотика в рацион кормления цыплят-бройлеров. Вариантов опытов четыре: контроль – без добавки пробиотика (группа 1) и три дозировки пробиотика «Olin»: 0,015; 0,022 и 0,029 г/гол. (группы 2, 3, 4 соответственно). Таким образом, сравниваемых

Начальный этап статистических исследований по сравнению средних заключается в визуальном анализе ящичковых диаграмм, иллюстрирующих различие медиан показателей и интервалов их варьирования по повторностям каждого опыта – рисунок 4 (помимо двух индикаторов качества полуфабриката, «чувствительных» к добавке пробиотика, рассматривали ещё два показателя – массу несъедобных частей и массу костей).

Визуальный просмотр ящичковых диаграмм показывает, что если для первых двух показателей – массы мышц и массы филе – средние экспериментальных групп, скорее всего, значимо отличаются от средних контрольной группы, то для второй пары показателей – массы несъедобных частей и массы костей – такого отличия не наблюдается: хотя медианы и заметно различаются, распределения этих показателей по повторностям сильно перекрываются. Это предположение подтверждают результаты, полученные с помощью однофакторного дисперсионного анализа процедуры « Compare Means (Сравнение средних)»: значения критерия Фишера F =37,5 и 66,4 для первых двух показателей – массы мышц и массы филе – статистически значимы на уровне не хуже 0,0005 и статистически незначимы для третьего и четвертого показателя ( р- уровень для них 0,429 и 0,395 соответственно) – таблица 3.

средних – четыре.

Таблица 3 - Дисперсионный анализ ведущих информативных показателей мясных качеств тушек цыплят-бройлеров

Показатель, г	Источник изменчивости	Сумма квадратов	Ст. св.	Средний квадрат	Критерий Фишера	Знч.
Масса мышц	Между группами	28213,458	3	9404,486	37,472	0,000
	В группах	5019,500	20	250,975
	Сумма	33232,958	23
Масса филе	Между группами	8597,125	3	2865,708	66,374	0,000
	В группах	863,500	20	43,175
	Сумма	9460,625	23
Масса несъедобных частей	Между группами	93,458	3	31,153	0,964	0,429
	В группах	646,500	20	32,325
	Сумма	739,958	23
Масса костей	Между группами	93,000	3	31,000	1,043	0,395
	В группах	594,333	20	29,717
	Сумма	687,333	23

Выполним теперь сравнение средних двух ведущих информативных показателей качества тушек – массы мышц и массы филе – традиционным методом по критерию Стьюдента, для двух эксперименталь- ных групп 3 и 4 (в пакете анализа данных SPSS Base для этого предусмотрена процедура «Compare Means (Сравнение средних)»). Полученные результаты приведены в таблицах 4 и 5.

Таблица 4 - Т -тест для независимых измерений показателя «Масса мышц» в опытах 3 и 4

	Критерий равенства дисперсий Ливиня		t -критерий равенства средних
	F	Знч.	t	Ст. св.	Знч. (2-сторон)	Средняя разность	Стд. ошибка разности	95% доверительный интервал разности
								нижняя граница	верхняя граница
Предполагается равенство дисперсий	0,007	0,935	2,273	10	0,046	21,00	9,239	0,415	41,585
Равенство дисперсий не предполагается			2,273	9,948	0,046	21,00	9,239	0,400	41,600

Таблица 5 - Т -тест для независимых измерений показателя «Масса филе» в опытах 3 и 4

	Критерий равенства дисперсий Ливиня		t -критерий равенства средних
	F	Знч.	t	Ст. св.	Знч. (2-сторон)	Средняя разность	Стд. ошибка разности	95% доверительный интервал разности
								нижняя граница	верхняя граница
Предполагается равенство дисперсий	0,010	0,921	3,168	10	0,010	10,83	3,420	3,214	18,453
Равенство дисперсий не предполагается			3,168	9,837	0,010	10,83	3,420	3,197	18,470

Из таблиц 4 и 5 следует, что согласно t -тесту 95-типроцентные доверительные интервалы разностей обоих показателей не включает в себя нуль, а следовательно, гипотеза о равенстве средних отвергается (заметим, что согласно критерию Ливиня, дисперсии значимо не различаются, вследствие чего 95-ти процентные доверительные интервалы разностей по строкам таблиц практически совпадают).

Критерию наименьшей существенной разности в пакете SPSS Base отвечает множественное сравнение средних по критерию LSD – Least Significant Difference в процедуре « General Linear Model (Общая линейная модель)» [1, 14]. Результаты множественного сравнения по традиционному подходу приведены в таблицах 6 и 7.

Таблица 6 - Парные сравнения средних показателя «Масса мышц» по критерию LSD

(I) Группа	(J) Группа	Средняя разность (I-J)	Стд. ошибка	Знч. (2-сторон)	95% доверительный интервал
					нижняя граница	верхняя граница
1	2	-34,83	9,146	0,001	-53,91	-15,75
	3	-90,17	9,146	0,000	-109,25	-71,09
	4	-69,17	9,146	0,000	-88,25	-50,09
2	1	34,83	9,146	0,001	15,75	53,91
	3	-55,33	9,146	0,000	-74,41	-36,25
	4	-34,33	9,146	0,001	-53,41	-15,25
3	1	90,17	9,146	0,000	71,09	109,25
	2	55,33	9,146	0,000	36,25	74,41
	4	21,00	9,146	0,033	1,92	40,08
4	1	69,17	9,146	0,000	50,09	88,25
	2	34,33	9,146	0,001	15,25	53,41
	3	-21,00	9,146	0,033	-40,08	-1,92

Таблица 7 - Парные сравнения средних показателя «Масса филе» по критерию LSD

(I) Группа	(J) Группа	Средняя разность (I-J)	Стд. ошибка	Знч. (2-сторон)	95% доверительный интервал
					нижняя граница	верхняя граница
1	2	-25,00	3,794	0,000	-32,91	-17,09
	3	-50,50	3,794	0,000	-58,41	-42,59
	4	-39,67	3,794	0,000	-47,58	-31,75
2	1	25,00	3,794	0,000	17,09	32,91
	3	-25,50	3,794	0,000	-33,41	-17,59
	4	-14,67	3,794	0,001	-22,58	-6,75
3	1	50,50	3,794	0,000	42,59	58,41
	2	25,50	3,794	0,000	17,59	33,41
	4	10,83	3,794	0,010	2,92	18,75
4	1	39,67	3,794	0,000	31,75	47,58
	2	14,67	3,794	0,001	6,75	22,58
	3	-10,83	3,794	0,010	-18,75	-2,92

Как следует из таблиц 6 и 7, все 95-типроцентные доверительные интервалы разностей обоих показателей не включает в себя нуль, следовательно, гипотеза о равенстве средних отвергается.

Иные результаты сравнения средних дает применение критерия Стьюдента с поправкой Бонферро-ни – таблица 8 (в целях сокращения объема раздела приведены данные для одного показателя – массы мышц).

Таблица 8 – Парные сравнения средних показателя «Масса мышц» по критерию Бонферрони

(I) Группа	(J) Группа	Средняя разность (I-J)	Стд. ошибка	Знч. (2-сторон)	95% доверительный интервал
					нижняя граница	верхняя граница
1	2	-34,83	9,146	0,007	-61,61	-8,06
	3	-90,17	9,146	0,000	-116,94	-63,39
	4	-69,17	9,146	0,000	-95,94	-42,39
2	1	34,83	9,146	0,007	8,06	61,61
	3	-55,33	9,146	0,000	-82,11	-28,56
	4	-34,33	9,146	0,008	-61,11	-7,56
3	1	90,17	9,146	0,000	63,39	116,94
	2	55,33	9,146	0,000	28,56	82,11
	4	21,00	9,146	0,196	-5,77	47,77
4	1	69,17	9,146	0,000	42,39	95,94
	2	34,33	9,146	0,008	7,56	61,11
	3	-21,00	9,146	0,196	-47,77	5,77

Сравнение таблиц 6 и 8 показывает, что уровни значимости в таблице 6 уже иные, отличаются и результаты сравнения средних: так, средняя масса мышц экспериментальной группы 3 больше среднего показателя группы 4 на 21 г, но по критерию LSD эта разность статистически незначима на уровне 0,033, тогда как по критерию Бонферрони значимость этой же разности составляет 0,196, что значительно превышает нормативный уровень 0,05. Иначе говоря, при более строгом подходе к сравнению средних эффект прибавки массы мышц полуфабриката цыплят-бройлеров при добавке в рацион питания пробиотика в количестве 0,022 и 0,029 г/гол. статистически неразличим.

Часто используется ещё более консервативный метод множественного сравнения Шеффе, который защищает от больших значений уровня ошибок в эксперименте. Применим его для сравнения средних масс мышц и массы филе полуфабриката – таблицы 9 и 10.

Таблица 9 – Апостериорные парные сравнения средних масс мышц по критерию Шеффе

(I) Группа	(J) Группа	Средняя разность (I-J)	Стд. ошибка	Знч. (2-сторон)	95% доверительный интервал
					нижняя граница	верхняя граница
1	2	-34,83	9,146	0,011	-62,72	-6,95
	3	-90,17	9,146	0,000	-118,05	-62,28
	4	-69,17	9,146	0,000	-97,05	-41,28
2	1	34,83	9,146	0,011	6,95	62,72
	3	-55,33	9,146	0,000	-83,22	-27,45
	4	-34,33	9,146	0,012	-62,22	-6,45
3	1	90,17	9,146	0,000	62,28	118,05
	2	55,33	9,146	0,000	27,45	83,22
	4	21,00	9,146	0,188	-6,89	48,89
4	1	69,17	9,146	0,000	41,28	97,05
	2	34,33	9,146	0,012	6,45	62,22
	3	-21,00	9,146	0,188	-48,89	6,89

Таблица 10 – Апостериорные парные сравнения средних масс филе по критерию Шеффе

(I) Группа	(J) Группа	Средняя разность (I-J)	Стд. ошибка	Знч. (2-сторон)	95% доверительный интервал
					нижняя граница	верхняя граница
1	2	-25,00	3,794	0,000	-36,57	-13,43
	3	-50,50	3,794	0,000	-62,07	-38,93
	4	-39,67	3,794	0,000	-51,23	-28,10
2	1	25,00	3,794	0,000	13,43	36,57
	3	-25,50	3,794	0,000	-37,07	-13,93
	4	-14,67	3,794	0,010	-26,23	-3,10
3	1	50,50	3,794	0,000	38,93	62,07
	2	25,50	3,794	0,000	13,93	37,07
	4	10,83	3,794	0,072	-0,73	22,40
4	1	39,67	3,794	0,000	28,10	51,23
	2	14,67	3,794	0,010	3,10	26,23
	3	-10,83	3,794	0,072	-22,40	0,73

Видно, что в качественном отношении результаты сравнения средних по критерию Шеффе идентичны сравнению по критерию Бонферрони, отличие наблюдается лишь в уровнях значимости и доверительных интервалах.

При сравнении средних по тесту Шеффе имеется также возможность выделить однородные подгруппы сравниваемых вариантов эксперимента. Ниже представлены таблицы однородных групп для двух показателей – массы мышц и массы филе.

Таблица 11 - Однородные подгруппы опытов по критерию Шеффе по показателю «масса мышц» (у ровень значимости критерия различия между подгруппами р =0,0 5)

Группа	Повторность	Масса мышц, г
		1	2	3
1 – контроль	6	933,50
2	6		968,33
4	6			1002,67
3	6			1023,67
Уровень значимости критерия различия в подгруппе		1,000	1,000	0,188

Таблица 12 - Однородные подгруппы опытов по критерию Шеффе по показателю «масса филе» (у ровень значимости критерия различия между подгруппами р =0,0 5)

Группа	Повторность	Масса мышц, г
		1	2	3
1 – контроль	6	332,33
2	6		357,33
4	6			372,00
3	6			382,83
Уровень значимости критерия различия в подгруппе		1,000	1,000	0,072

Поясним таблицы 11 и 12. По обоим показателям, согласно тесту Шеффе, опыты образуют три однородные подгруппы. В подгруппу 1 входит контрольная группа 1, в подгруппу 2 – экспериментальная группа 2 с дозировкой пробиотика «Olin» 0,015 г/гол., в подгруппу 3 – экспериментальные группы 3 и 4 с дозировкой пробиотика «Olin» 0,022 и 0,029 г/гол. И по массе мышц, и по массе филе средние по экспериментальным группам 3 и 4 статистически неразличимы, т.е. увеличение дозировки пробиотика с 0,022 г/гол. до 0,029 г/гол. эффекта не дает.

Заметим, что результаты, приведенные в таблицах 6-12, можно также получить с помощью однофакторного дисперсионного анализа процедуры « Compare Means (Сравнение средних)» пакета SPSS Base . В данном исследовании мы воспользовались другой процедурой – « General Linear Model (Общая линейная модель)», полезным результатом которой, в дополнение к этим таблицам, является возможность получить МНК-оценки параметров модели. Пример таблицы МНК-оценок параметров такой модели для одного из информативных показателей – массы мышц – приведен ниже.

Таблица 13 - Оценки параметров линейной модели для информативного показателя «Массы мышц»

(за нулевой уровень принята группа 4)

Параметр	B	Стд. ошибка	t	Значимость	99% доверительный интервал
					нижняя граница	нижняя граница
Постоянная	1002,667	6,468	155,030	0,000	989,176	1016,158
[ГРУППА=1]	-69,167	9,146	-7,562	0,000	-88,246	-50,087
[ГРУППА=2]	-34,333	9,146	-3,754	0,001	-53,413	-15,254
[ГРУППА=3]	21,000	9,146	2,296	0,033	1,921	40,079
[ГРУППА=4]	0	,	,	,	,	,

Поясним таблицу 13. В математической форме однофакторная линейная модель дисперсионного анализа записывается следующим образом:

Yi = µ0 + αi + εi, (1) где Yi – наблюдаемое значение выходной переменной Y на i-м уровне фактора; µ0 – оценка свободного коэффициента модели; αi – оценки главных эффектов на i-м уровне; εi – случайная ошибка. МНК-оценки параметров модели (2) и приведены в таблице 13.

В этой таблице постоянная µ0=1002,667 г, а за нулевой принят эффект группы 4, т.е. средняя масса мышц цыплят-бройлеров группы 4 принята равной µ0=1002,667 г. Эффекты (добавки массы мышц) других групп отсчитываются уже от этого уровня; так, средняя масса мышц цыплят-бройлеров группы 1 (эталона) характеризуется добавкой ai=-69,167 г, с доверительным 95%-ым интервалом (-88,246 .. -50,087) г, что соответствует средним значениям массы мышц (914,421 … 952,580) г. Соответственно, группа 3 характеризуется максимальным эффектом аз=21,000 г, с доверительным 95%-ым интервалом (1,921 .

40,079) г, что соответствует средним значениям показателя (1004,588 . 1042,746) г.

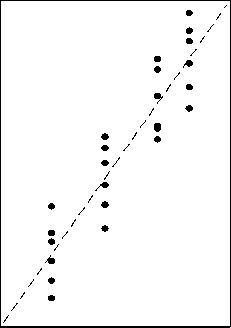
Эта однофакторная модель характеризуется достаточно высоким значением коэффициента детерминации: она объясняет 84,9% общей дисперсии. Судя по графикам остатков, представленным на рисунке 5, модель адекватна: метки, отвечающие эмпирическим данным, расположены достаточно близко к линии регрессии (рисунок 5 а ), а остатки на рисунке 5 б образуют равномерную полосу вдоль предсказанных значений показателя, что свидетельствует об отсутствии эффекта гетероскедастичности.

Rsq = 0 8490

900      950      1000     1050

Расчетные значения, г

б

-20

-40

Масса мышц, г (расчет)

Рис. 5 – Характеристики качества линейной модели дисперсионного анализа массы мышц полуфабриката цыплят-бройлеров: а – связь эмпирических значений показателя с расчетными;

б – график остатков

Однофакторная модель для второго информативного показателя - массы филе - также имеет высокие характеристики качества: коэффициент детерминации R ²=0,909, т.е. она объясняет 90,9% общей дисперсии (таблица МНК-оценок параметров этой модели не приводится ради сокращения объема раздела).

Представленные выше модели дисперсионного анализа отражают связь выходных переменных не с количественной независимой переменной (предиктором), а с уровнями номинальной переменной (в данном случае, с номером опытной группы), и не являются регрессионными моделями в классическом понимании этого термина. Они позволяют выполнить сравнение вариантов эксперимента, но не позволяют а

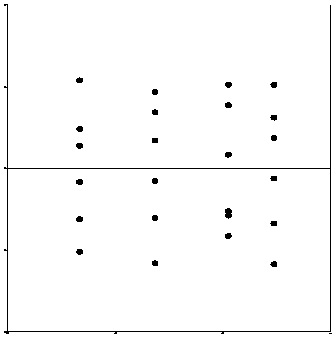
Группа

Рис. 6 – Распределение расчетных значений ведущих показателей мясных качеств тушек цыплят-бройлеров по опытным группам: а – масса мышц; б – масса филе

решить оптимизационные задачи. В этой связи, задачей данного раздела является разработка регрессионных моделей, отражающих зависимость ведущих информативных показателей мясных качеств полуфабриката от содержания пробиотика, с последующей их оптимизацией.

Отправные данные для решения сформулированной задачи, полученные нами ранее с помощью процедуры « General Linear Model (Общая линейная модель)» пакета программ статистического анализа данных общественных наук SPSS Base , в наглядной графической форме отражают диаграммы, представленные на рисунке 6.

б

Группа

Поясним рисунок 6. Числа 1 … 4 на горизонтальной оси – это номера групп в эксперименте по влиянию экспериментальных дозировок пробиотика «Olin» на информативные показатели – массу мышц и массу филе, при этом 1 – номер контрольного опыта, который предполагал основной рацион кормления цыплят-бройлеров без добавки пробиотика, 2, 3, 4 – номера опытов с дозировки пробиотика «Olin» 0; 0,015; 0,022 и 0,029 г/гол. На первый взгляд, можно а было бы сопоставить номерам групп количественную переменную – дозировку пробиотика в интервале от 0 до 0,029 г/гол., а затем строить модель регрессии. Но такой прием не вполне корректен, следует рассматривать не четыре, а лишь три уровня дозировки пробиотика «Olin»: 0,015; 0,022 и 0,029 г/гол. Тогда мы получаем несколько иной вид зависимости информативных показателей мясных качеств тушек цыплят-бройлеров от дозировки пробиотика – рисунок 7.

б

Rsq = 0 7087

,010  ,015  ,020  ,025  ,030  ,035

Дозировка пробиотика, г/гол

Rsq = 0 7697

,010  ,015  ,020  ,025  ,030  ,035

Дозировка пробиотика, г/гол

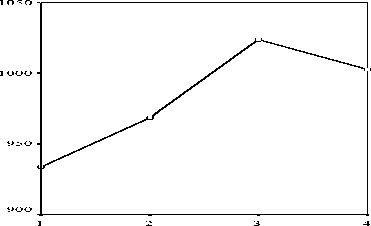
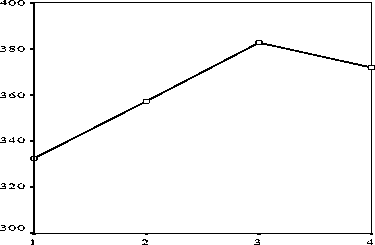
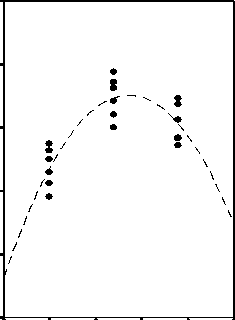
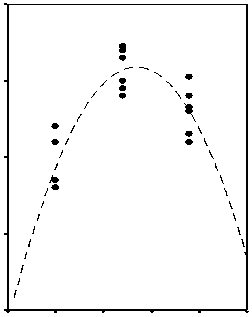
Рис. 7 – Зависимость ведущих информативных показателей мясных качеств тушек цыплят-бройлеров от дозировки пробиотика: а – масса мышц; б – масса филе

Графики рисунка 7 построены с помощью графической процедуры « Scatterplot » программы SPSS Base , по исходным данным эксперимента, выполненного с шестикратной повторностью. Из рисунка следует, что, несмотря на довольно высокую вариабельность исходных данных по повторностям, коэффициент полиномиальной детерминации достаточно высок: 0,709 для квадратичной модели массы мышц и 0,770 – для квадратичной модели массы филе (для построения кубической регрессии трех градаций независимой переменной недостаточно).

Судя по характеру кривых регрессии квадратичной корреляции, максимумы обоих информативных показателей достигаются при дозировке пробиотика примерно 0,024 г/гол., и для уточнения этого значения нами с помощью процедуры множественной линейной регрессии определены параметры квадратичных моделей

Y = b 0 + b 1 Х + b 1 Х ², (2)

где Х – дозировка пробиотика, b 0 , b 1 и b 2 – оцениваемые коэффициенты моделей.

Для оценки параметров квадратичных моделей предварительно в редакторе данных формировали переменную X ², затем был реализован метод « Enter », т.е. независимые переменные Х и Х ² вводили в анализ принудительно. Полученные результаты аппроксимации эмпирических данных квадратичными моделями представлены в таблице 14.

Таблица 14 – МНК-оценки параметров квадратичных моделей

Зависимая переменная	Предиктор	Нестандартизированные коэффициенты		Стандартизир. коэффициенты (бета-коэффициенты)	t	Знч.
		B	Ст. ошибка
Масса мышц	Постоянная	592,721	75,276		7,874	0,000
	Х	36724,490	7221,423	7,748	5,085	0,000
	Х 2	-778911,565	163435,286	-7,261	-4,766	0,000
Масса филе	Постоянная	180,344	29,430		6,128	0,000
	Х	17360,544	2823,290	8,331	6,149	0,000
	Х 2	-370748,299	63896,710	-7,861	-5,802	0,000

Как следует из таблицы 14, коэффициенты квадратичных моделей, отражающих зависимость массы мышц и массы филе тушек цыплят-бройлеров от дозировки пробиотика «Olin» в комбикормах, значимы на уровне не хуже 0,0005. В целом модели характери- зуются достаточно высоким качеством: коэффициент детерминации 0,709 и 0,770 для массы мышц и филе соответственно, значения критерия Фишера – 18,2 и 25,1 соответственно статистически значимы на уровне не не хуже 0,0005.

Это позволяет использовать квадратичные модели, явный вид которых для массы мышц:

Y 1 = 592,7 +3 6724,5 Х – 778912 Х ²; (3)

для массы филе:

Y 2 = 180,3 + 17360,5 Х – 370748 Х ², (4)

Дифференцируя модели (3) и (4) по Х , после приравнивания полученных выражений нулю получаем:

Х 1опт = 36724,5 / (2*778912) = 0,0236 г/гол.;  (4)

Х 2опт = 17360,5 / (2*370748) = 0,0234 г/гол.  (5)

Полученные оценки практически совпадают. Это позволяет выполнить их усреднение и заключить, что дозировка пробиотика «Olin» в комбикормах, обеспечивающая максимум ведущих показателей мясных качеств тушек цыплят-бройлеров, составляет 0,0235 г/гол.

Выводы. Представленные выше результаты обработки эмпирических данных по влиянию спорогенного пробиотика «Olin» на убойные и мясные качества тушек цыплят-бройлеров убедительно демонстрируют дополнительные возможности, получаемые при комплексном использовании статистических методов, алгоритмы которых поддерживаются современными программами анализа данных. Уже применение достаточно ранней версии пакета программ статистического анализа данных общественных наук

SPSS Base позволило получить новые знания, среди которых: выявление ведущих информативных показателей качества полуфабриката; сокращение размерности изучаемого множества показателей; оценка значимости влияния экспериментальных дозировок пробиотика « Olin », по сравнению с контролем, на информативные показатели; уточнение оптимальной дозировки пробиотика «Olin» в комбикормах по критериям качества полуфабриката.

Полученные положительные результаты выполненных исследований позволяют рекомендовать комплексное использование исследователями в различных областях сельскохозяйственного производства таких статистических методов для анализа эмпирических данных, как корреляционно-регрессионный и факторный анализ, дисперсионный анализ и его сравнительно новый метод – общую линейную модель.

Успех применения представленных статистических методов во многом определяется уровнем подготовки специалистов сельского хозяйства в высших учебных заведениях, и в этой связи следует рекомендовать всемерное использование в учебном процессе, наряду с традиционными информационными технологиями из пакета офисных программ MS Office , современных программ анализа данных, таких, как SPSS , STATGRAPHICS PLUS , STATISTICA .