Математические методы в теории чистого изгиба прямоугольных балок из разупрочняющегося материала с симметричной диаграммой растяжения-сжатия

Разрушение есть явление того же порядка, что и невозможность равновесия [1], сопровождающееся к тому же потерей устойчивости процесса деформирования. Для определения момента потери устойчивости (момента разрушения) необходимо учитывать как устойчивое (упрочнение), так и неустойчивое (разупрочнение) состояния материала. Краевые задачи с соответствующими определяющими соотношениями позволяют находить все положения равновесия конструктивного элемента (устойчивые и неустойчивые) и, следовательно, прогнозировать разрушение. Очевидно, что расчет напряженно-деформированного состояния элементов конструкций требует применения в данном случае специальных математических методов, нетрадиционных для механики сплошных сред. Такие методы разработаны в математической теории катастроф и в теории особенностей дифференцируемых отображений [2, 3].

В силу сложности решения в общей постановке задач устойчивости процесса деформирования анализ необходимо начинать с исследования устойчивости простых механических систем и конструктивных элементов, материал которых обладает свойством деформационного разупрочнения. Тогда полученные результаты становятся модельными примерами для общей теории, помогают установить связь между теорией и практикой и способствуют лучшему пониманию физической сути явления.

В данной работе рассматривается чистый изгиб балки прямоугольного поперечного сечения. Балка изготовлена из материала с падающей диаграммой, характеризующей все стадии деформирования (упрочнение и разупрочнение) при одноосном растяжении и сжатии. Предполагается, что диаграммы растяжения и сжатия симметричны. В отличие от предыдущих работ по данной тематике (например [4–6]), здесь используются общие математические методы решения нелинейных задач (метод Ньютона–Канторовича, позволяющий при корректном выборе начального приближения рассчитать напряженно-деформированное состояние для всевозможных положений равновесия; метод простой итерации; метод исследования устойчивости по линейному приближению), а также методика, разработанная в математической теории катастроф. Апробация этих методов на задаче чистого изгиба балки из разупрочняющегося материала позволяет использовать их и при решении неодномерных задач механики разупрочняющегося твердого тела.

2.    Постановка задачи

Достаточно длинная балка с прямоугольным сечением подвергается чистому изгибу. Высота и ширина балки соответственно равны 2h и b . Деформирование осуществляется квазистатически при неизменной температуре либо монотонно возрастающим изгибающим моментом M (мягкое нагружение), либо за счет монотонного увеличения кривизны балки к (жесткое нагружение). В случае чистого изгиба единственной ненулевой компонентой тензора напряжений является продольное напряжение стx = ст(у), а продольная деформация sx = s(у) линейно распределяется по высоте балки [7] (Рис. 1).

Свойства материала при растяжении и сжатии будем описывать четной потенциальной функцией (потенциалом напряжений) П ( s ), монотонно возрастающей от нуля на отрезке |^0, s Z ] и принимающей постоянное значение при s>s Z , причем производная П , _Е ( s = 0) = 0. Кроме того, на участке |^0, s B )

функция П выпукла вниз (вторая производная П,ss > 0), на участке (sB, sZ ] — выпукла вверх (П,ЕЕ < 0), а точка s = sB

есть точка

перегиба ( п , _ее ( s = s B ) = 0 ) . Выпуклость

вниз потенциальной функции отвечает

устойчивым состояниям материала (упрочнению), выпуклость вверх — неустойчивым (разупрочнению), точка перегиба — пограничному состоянию [8].

балки

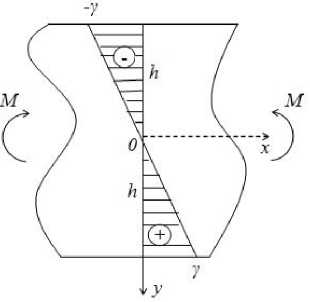
Рис. 1. Распределение продольных деформаций;

Y = £ ( h ) - деформация наиболее растянутых волокон

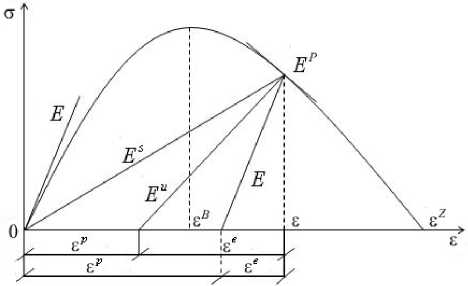
Рис. 2. Полная диаграмма деформирования при растяжении и модули разгрузки для различных материалов ( s B - деформация предела прочности, s Z - деформация разрушения)

При сделанных предположениях зависимость между напряжениями и деформациями задает формула ct(s) = П Е, которая определяет полную диаграмму растяжения, обладающую восходящей и ниспадающей (вообще говоря, до нуля) ветвями (Рис. 2). Диаграмма сжатия симметрична относительно начала координат в силу четности потенциальной функции. Следовательно, положение нейтральной плоскости, в точках которой продольные напряжения и деформации равны нулю, неизменно. Наклон диаграмм при сжатии и растяжении характеризует четная функция EP = ст s = (П s) = П ss, имеющая смысл касательного модуля (модуля тангенциальной жесткости). Ясно, что при EP > 0 материал находится в состоянии упрочнения, если же EP < 0, то в состоянии разупрочнения. Выражение для касательного модуля определяет инкрементальное соотношение, связывающее приращения деформаций и напряжений, а именно s dст = EPds. Отсюда следует, что ст = j EPds .

s

Физический смысл введенного потенциала вытекает из равенства П = J CT d s , представляющего собой 0

работу напряжения, затраченную на деформирование. Тогда площадь под полной диаграммой численно равняется работе, которую необходимо затратить на разрушение материала в условиях жесткого растяжения при равновесном характере деформирования, сохраняющемся вплоть до разделения материального элемента на фрагменты.

Очевидно, что при любом распределении напряжений и деформаций по высоте балки, связанном с диаграммой ct ( s ) , где s = к у , тождественно удовлетворяются дифференциальные уравнения равновесия и условия совместности. Требуется только выполнение граничных условий на торцах балки, а именно равенство нулю главного вектора и главного момента напряжений [7]:

h b J g dy = 0,

- h

b J g ■ ydy = 2 b J g ■ ydy

h

h

= M .

- h

Равенства (1) также играют роль статических уравнений равновесия и должны удовлетворяться в каждом поперечном сечении балки. Первое равенство в выражениях (1) выполняется тождественно в силу нечетности функции g ( y ), а второе можно переписать в виде операторного уравнения

Ф ( к , M ) = 0,                                             (2)

где

h

Ф ( к , M ) = f ( к ) - M = 2 b J g ( k y ) ydy - M

есть нелинейный оператор, заданный на множестве

{к,M : 0 < к < кZ = eZ/h, 0 < M < Mmax}. Максимальное значение изгибающего момента Mmax совпадает с максимумом функции f (к), который достигается при значении к = кm, удовлетворяющем уравнению fк= 2bJP = 0 , где

J P = h E P ( к y ) y²dy = -1 3- J E P ( e ) e ² d e = -1 3- ^f y ² g ( y ) - 2 J G ( e ) e d e^ .                     (3)

0                ^к 0              ^к I           0         J

Здесь у — деформация наиболее растянутых волокон; J P — мгновенная жесткость балки при изгибе;

e интегрирование проведено по частям с учетом того, что g = J EPde.

Наличие в балке областей разупрочненного материала, появляющихся в ходе нагружения, может привести к потере устойчивости процесса деформирования (к разрушению балки). Отсюда возникает следующая задача: для заданной диаграммы G ( e ), описывающей стадии упрочнения и разупрочнения материала, найти все положения равновесия балки (решения уравнения (2)) и определить их устойчивость.

• 3.    Определяющие соотношения

Отклонение диаграммы деформирования от прямолинейного участка упругости объясняется диссипативными процессами, происходящими в материале. Обычно различают механическую диссипацию, обусловленную пластической деформацией, и континуальное разрушение, характеризуемое поврежденностью, вызванной нарушением сплошности.

Для определения параметров диссипации и их связи с потенциальной функцией П запишем уравнение второго закона термодинамики с учетом необратимости и изотермичности процесса деформирования в виде [1] dF = ( 1/ p ) g d e- dg , где F — свободная энергия, р — плотность материала, g d e = d П — элементарная работа напряжений, dg >  0 — диссипация. Параметрами термодинамического состояния являются упругая ( e ^e ) и пластическая ( e p ) составляющие полной деформации ( e = e ^e + e p ) и параметр ю , характеризующий поврежденность материала. Полагаем, что упругие свойства материала не зависят от пластических деформаций [1], то есть F = F ( e ^e , ю ) . Тогда, учитывая равенство d e = d e ^e + d e p , имеем ^{д F} 1 e . ^{д F} 1          \    1 e . 1 p \ 1         f ^{д F}     /-^ 1 _e f^{d F} i / l\ ip , r ) a            rn

---de +--dto = (Up)g de + dep -dg , или--g/p de + —d®-(g/p)dep + dg = 0 . Отсюда [1] dee        дю x 2 v 7              Idee        J Id® v                 J дF g = р---, dee

р dg = g d e ^p -p— d ю = dg^p + dg ^ю , дю

, n n                                              ю       dF , где dgp =gdep — механическая диссипация, dg =-p—dю — диссипация континуального разрушения. дю

Зададим свободную энергию формулой

F = ( 1/ р ) ( E e ^e e ^e /2 - ю E e ^e e ^e /2 ) .

Здесь E б e б e /2 есть потенциальная энергия упругих деформаций, возникающих благодаря механической диссипации (результат релаксации напряжений вследствие пластической деформации), а второй член — это энергия, дополнительно потерянная из-за континуального разрушения (результат релаксации напряжений вследствие хрупких микроразрушений). Таким образом, функция F определяет ту часть внутренней энергии, которая может быть возвращена в результате разгрузки.

Будем различать три типа материалов: упругопластический — это материал, в котором диссипация происходит за счет образования только пластических деформаций ( б ^p * 0 , ю = 0, модуль разгрузки равен модулю Юнга E ); упругохрупкий — материал, в котором диссипация происходит только за счет континуального разрушения ( б ^p = 0 , ю * 0 , модуль разгрузки равен секущему модулю E^s = g/б ); партипластический (частично пластический) — материал, в котором имеют место оба вида диссипации ( б ^p * 0, ю * 0 , модуль разгрузки равен E^u = g/б e = g/(б — б ^p ) ).

Теперь, подставляя выражение (5) в формулу (4), находим, что в общем случае для партипластического материала g = E (1 — ю)(б —б p),(6)

где E (1 — ю) = Eu и, следовательно, ю = 1 - Eu/E. Из равенства (6) вытекает уравнение для определения пластической составляющей полной деформации, а именно бp = б-—= б-Пб = б—-fEPdб    (g = П = БП dб).(7)

Eu        Eu        Eu J               v       ,б J . 'v )

Дифференцируя выражение (7) по переменной б с учетом вида функции Eu = E (1 — ю), получаем дифференциальное уравнение (б-бр (б))ю,б + ю(б) + (1 -ю(б))брб = 1 -EP(б)/E (EP = ПББ), или d(бю)-d(бpю) + dБp = (1 -EP/E)dБ , которое увязывает кинетику формирования диссипативных параметров материала с изменением потенциальной функции П . Для упругопластического материала (Eu = E , ю = 0) имеем g = E(б-бр), бр =б-(1/E)JEPdБ    (dБp = (1 -EP /E)dб),(8)

а для упругохрупкого (Eu = Es, бр = 0) находим g = E^ = E(1 — ю)б, ю = 1 -Es/E , бю,б +ю = 1 -EP /E (d(бю) = (1 -EP /E)dб).(9)

Покажем, что приведенные модели не противоречат термодинамике, то есть диссипация всегда положительна. Запишем выражения диссипации континуального разрушения и механической диссипации в общем случае для партипластического материала:

dgю = EБ e^d ю/ 2 = (EБe Бе /2) d (1 — E^E) = (Esese /2)(— dE^E),(10)

dgp =gdБp =g-d(б-g/Eu) = g(1 — EP /Eu)dБ + (g2/(Eu)2)dEu (g = JEpdб).(11)

Выражение (10) всегда больше или равно нулю (dEu < 0). Это же справедливо и для упругохрупкого материала (Eu = Es, dEs < 0 ). В (11) первое слагаемое всегда положительно ( g> 0, dб > 0, Eu > 0 , Eu > EP), а второе слагаемое отрицательно. Неравенство dgp > 0 выполняется в случае, когда EБ > — Eu (Eu — EP) / g . Данное неравенство накладывает обусловленное континуальным разрушением ограничение на скорость убывания модуля разгрузки. В случае упругопластического материала (Eu = E) неравенство dgp > 0 всегда справедливо. Наконец разрушение материала соответствует тому его состоянию, в котором приращение энергии dП = 0 . Отсюда П = g = 0, П ББ = EP = 0, Eu = 0 , Es = 0, e = ep, se = 0 , to = 1. Следовательно, разрушенный материал не способен накапливать и диссипировать (dgs = 0 , dgp = 0) подводимую энергию.

4.    Условия существования решения операторного уравнения (2)

Уравнение связи (2) между переменными к и M может определять одну из них как неявную функцию другой. Эта неявная функция представляет собой решение данного уравнения [9]. Поэтому условия существования решения уравнения (2) задается теоремой о неявной функции [9]. Здесь применимо следствие из теоремы о неявной функции, а именно теорема о существовании обратного оператора f ^{- 1} [9].

Пусть момент M — задаваемая величина (параметр управления). Тогда, если функция f ( к ) имеет отличную от нуля и сохраняющую знак производную в некоторой окрестности точки к’ , то для этой функции в данной окрестности существует обратная функция (решение уравнения (2)) к = f ^{- 1} ( M ) , определенная в некоторой окрестности точки M ‘ , где M' = f ( к‘ ) . Таким образом, функция f ( к ) в окрестности точки к’ устанавливает взаимно-однозначное соответствие между этой окрестностью и множеством точек, образованным в данной окрестности значениями функции f ( к ) .

В точке к = к m имеем f _к = 0 , и уравнение (2) не определяет в окрестности точки к m переменную к как неявную функцию от M . Однако в самой точке к m существует единственное решение ф ( к m , M max ) = 0 . Для M >  M max решение уравнения (2) не существует. Если параметр к — задаваемая величина, то производная Ф , M * 0, и уравнение (2) всегда определяет однозначную функцию M от к , а именно M = f ( к ) .

5.    Определение зависимости изгибающего момента от кривизны(итерационная схема Ньютона–Канторовича)

Для нахождения решений уравнения (2), которое задает зависимость изгибающего момента от кривизны, применим итерационный метод Ньютона–Канторовича, использующий последовательную линеаризацию нелинейных уравнений [10]. В данной задаче схема Ньютона–Канторовича реализуется следующим образом. Допустим, что приближение к n найдено. Тогда для отыскания приближения к n _{+ 1} уравнение (2) заменим линеаризованным в точке к n уравнением Ф ( к n , M ) + Ф_к ( к n , M )( к-к n ) = 0. Если существует обратный линейный оператор [Ф _к ( к n , M ) ] 1 , то приходим к выражению для к n _{+ 1}:

кn+1 =кn -[ф,к(кn,M)]" ф(кn,M)

где Ф , _к = 2 bJ^p , и формула (12) принимает вид к _{n + 1} =к _n -I 2 b J ст ( к n y ) ydy - M I /(2 bJ^p )

Очевидно, что метод не реализуем, если на некотором итерационном шаге величина J ^p обращается в нуль. Здесь величина J ^p задается равенством (3). Кроме того, следует выбирать такие начальные приближения к ₀, при которых метод Ньютона-Канторовича сходится [11]. Для этого, во-первых, необходимо, чтобы точка к ₀ принадлежала отрезку, где выполняются следующие условия [12]: функция Ф и её производные Ф _к и Ф _кк непрерывны; значения функции Ф на концах отрезка имеют разные знаки; обе производные внутри отрезка сохраняют знак. Во-вторых, начальное приближение к ₀ в таком промежутке нужно брать в той его части, где выполняется неравенство Ф ( к ₀, M ) Ф _кк ( к ₀, M ) >  0, то есть функция Ф и её вторая производная имеют одинаковые знаки [12]. Отметим, что точки, разделяющие отрезок |^0, к Z ] на указанные выше промежутки при фиксированной величине M , следует искать среди точек экстремумов функции Ф , между которыми производная Ф _к сохраняет знак и существует обратный оператор [Ф _{> к} ] ( J^p * 0), и среди точек перегиба, между которыми сохраняет знак вторая производная.

В качестве примера рассмотрим чистый изгиб балки высотой h = 10 мм и шириной b = 1 мм. Полную диаграмму растяжения материала зададим функцией ст = E s exp ( -s/s B ) , где E = 2 - 10 4 кГ/мм², s B = 0,01.

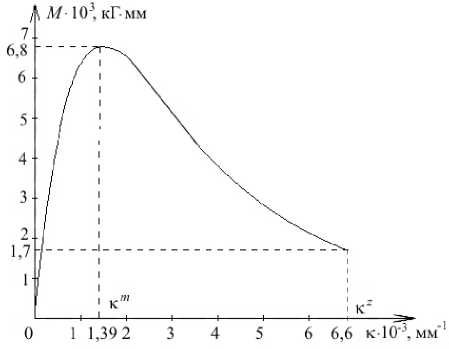
Рис. 3. Типичная диаграмма M (к), отвечающая полной диаграмме о(б)

Считаем, что материал разрушен, если б>б Z = 0,066 . Точка максимума функции Ф ( к , M ) есть к m = 0,00139мм ^{- 1}, точка перегиба

—  к t = 0,00284 мм-1. Эти точки образуют интервалы (0, кm), (кm, кt), (кt, кz), на которых, соответственно, Ф > 0,   Ф>кк < 0; Ф < 0,

Ф _, < 0; Ф, < 0, Ф ^ > 0. Если возле концов ,кк                 ,к                 ,кк первого промежутка функция Ф имеет разные знаки (Ф(0,M)< 0, Ф(кm,M)> 0) при заданном значении M , то для определения корня уравнения (2) начальное приближения выбираем вблизи левого конца промежутка. Если на втором промежутке ф(к m, M )> 0, ф(к t, M )< 0, то начальное приближение находим возле правого конца. Для третьего промежутка, в случае ф(к t, M )> 0,       Ф(к z, M )< 0,      начальное приближение берём вблизи левого конца. После проведения вычислений полученную зависимость M (к) дополняем точками M (0) = 0, M (кm ) = f (кm) и M (кt ) = f (кt). Рассчитанная диаграмма M (к) показана на рисунке 3. Таким образом, метод Ньютона–Канторовича позволяет установить все положения равновесия балки, как устойчивые, так и неустойчивые, отвечающие падающей ветви диаграммы M (к).

6.    Определение зависимости изгибающего момента от кривизны (схема простой итерации)

Перепишем уравнение (2), используя выражение для напряжений (6) (партипластический материал), в котором положим б = к у , в виде

J - MФ = M ,

где

h

J u = 2 b J E^u ( к у ) у ² dy ,

M Ф

^к у

= 2bJEu (ку)бp (ку)ydy = 2bJEu (ку) ку - (1/(Eu (ку))) J EPde

h

h

0                                         0                                               0

ydy . Здесь

функция Ju (к) имеет смысл изгибной жесткости упругой неоднородной балки, распределение модулей по сечению которой задаётся функцией E" (ку), определяемой по диаграмме деформирования материала, а функция MФ (к) — это фиктивный изгибающий момент, рассчитанный по величинам псевдонапряжений Euбp, где бp (ку) определяются по формуле (7). Равенство (13) преобразуем в операторное уравнение к = Ак

с нелинейным оператором Ак = U ( к ) + V ( к ) , U ( к ) = M ^Ф/ J u ( к ) , V ( к ) = mJ ( к ) , при этом V — кривизна упругой неоднородной балки с жесткостью J ^u , возникающая под действием момента M , а U — кривизна такой же балки при воздействии фиктивного момента M ^Ф .

Будем искать решение уравнения (14) методом последовательных приближений, применяя схему простой итерации [13], а именно кn+1 = Акn     (n = 0,1,2,...).

Приближения сходятся к решению уравнения (14), если на каждом итерационном шаге оператор А является сжимающим оператором [11], то есть удовлетворяет условию Липшица Ц Ак'-Ак"|| <  q\ |к'-к"|| с константой q <  1 ( q — коэффициент сжатия). Константа Липшица равна q = sup||А_к ||, где в общем случае к

А,к есть производная Фреше нелинейного оператора [13]. В данной задаче, используя равенство (13), имеем dAH M Ф Ju-(M + M °) J^ Ju )2 = ( M^-^J,к)/ Ju

Расписывая производные и делая затем

j к кh                                            к h замену y = е/к, получаем (к3 Ju /( 2 b))= j(Eueep + Eu e pE-Euee)e? d e=j[(E“e p + Eu e pe - Euee-Eu) + dк 0V ,              ’       ’                0^ •              ’’ к h ,                                                  к hк

+ E^u ]e ² d e = J { -[ E u ( e-e p ) ] + E u } e ² d e= J ( E u -G_e ) e ² d e = J ( E u - E P ) e ² d e .

0                              ,e          )               00

Делая обратную замену, окончательно находим

— = ( Ju -2bJp)/Ju = 1 -2bJp J .(16)

d к '

Здесь J^u >  0 . Тогда константа Липшица меньше единицы при J p >  0 , а при J p <  0 — больше единицы. Таким образом, если на каждом шаге величина J p >  0, то процесс (15) сходится, когда же, начиная с некоторого шага, J ^p становится меньше нуля, то процесс (15) начинает расходиться.

Обращение интеграла J ^p в нуль является необходимым условием начала расходимости итерационного процесса. Покажем, что это — и достаточное условие. Действительно, знак производной J p = к^{- 3} у ² E P ( у ) зависит только от знака модуля E P . При E P >  0 производная положительна и, следовательно, функция J p монотонно возрастает, при E P <  0 функция J p монотонно убывает. Это убывание естественно продолжается и после обращения интеграла J p в нуль. Отсюда на всех последующих итерациях J p <  0, константа Липшица больше единицы и процесс становится расходящимся.

Если балка изготовлена из упругопластического материала (8), который отличается от рассмотренного партипластического материала только тем, что имеет постоянный модуль разгрузки, равный модулю Юнга E , то J^u = 2 bh ³ E /3 . Подставляя это значение в формулу (16), находим, что процесс расходится с момента выполнения условия J p = 0 .

Для упругохрупкого материала (9) в уравнении (14) имеем M ф = 0 (ep = 0), Ju = Js, h где Js (к) = 2bJEs (кy)y2dy — жесткость упругой неоднородной балки, распределение секущих модулей 0

по сечению которой задано функцией Es (ку). Тогда в формуле (16) следует заменить параметр Ju на величину Js . Отсюда получаем, что и в данном случае итерационный процесс будет расходиться с момента обращения интеграла J p в нуль. Таким образом, использование схемы простой итерации (15) позволяет получить только восходящую ветвь диаграммы M~к (Рис. 3).

Отметим, наконец, что при жестком нагружении, когда задается величина кривизны к , уравнение (13) определяет изгибающий момент как однозначную функцию f ( к ) = k J ^u ( к ) - M ^ф ( к ) , и эта функция, следовательно, полностью описывает диаграмму M ~ к , изображенную на рисунке 3.

7.    Устойчивость процесса деформирования

Для изучения процесса устойчивости равновесия балки применим аппарат теории катастроф [2, 14], исходя из того, что каждый элемент находится в состоянии активного деформирования. В этом случае материал балки неотличим от нелинейно-упругого материала, и поэтому существует потенциал напряжений в виде работы деформаций материального элемента, а именно A (e) = J п(e) de . Очевидно, что функция A четная. Теперь, считая изгибающий момент M параметром управления, а кривизну к балки

h

параметром состояния, запишем выражение для

полной энергии П ( M , к ) = 2 b J A ( к у ) dy - J Md к , ( e = к у ) .

Эта потенциальная функция задает однопараметрическое семейство функций параметров состояний.

Критические точки функции П определяет уравнение П к = 0, которое является уравнением равновесия (1), связывающим параметры управления и состояния в положениях равновесия балки (устойчивых или неустойчивых). Вырожденные критические точки, в которых происходит смена типа равновесия, находятся из совместного решения уравнения (1) и уравнения д2П     Гд^ де Л          2л  ЭАГР л

—т- = 2 b--уау = 2 b E^py dy = 2 bJ' p = 0.

дк ' де дк 00

Если величина J p >  0, то функция П выпукла вниз

( п_кк >  0 ) и состояние балки устойчивое [8]. Когда J p <  0, функция П выпукла вверх, состояние неустойчивое. Равенство П _кк = 0 обусловливает точку перегиба, состояние равновесия пограничное. При постепенном возрастании изгибающего момента и J p >  0 , согласно принципу промедления [2], балка будет сохранять устойчивое равновесие до тех пор, пока интеграл J ^p не обратится в нуль. В этот момент критическая точка, отвечающая данному положению равновесия, становится вырожденной, а балка попадает в пограничное состояние. Любое малейшее возмущение приводит к потере устойчивости процесса нагружения. Очевидно, что за этим следует разрушение балки. Более того, момент потери устойчивости процесса деформирования балки является, как показано в предыдущем разделе, и началом расходимости итерационного процесса по схеме простой итерации. Таким образом, достижение интегралом J ^p нулевого значения (потеря устойчивости процесса деформирования) не позволяет использовать и метод Ньютона–Канторовича для определения параметров равновесия балки.

8.    Устойчивость по линейному приближению

Исследуем устойчивость положения равновесия балки с параметрами к ₀, M 0 , E ₀ p = E p ( к ₀ у ) , E 0 = E u ( к ₀ у ) . Возмутим это равновесие, увеличив изгибающий момент на малую величину dM >  0, и запишем уравнение возмущенного равновесия, используя формулу (13):

к ' = M'/j^u ( к ' ) + M ^ф ( к ')/ J u ( к ' ) .                                   (17)

Здесь к ' = к ₀ + d к , M ' = M ₀ + dM ,

h

Mф(к') = 2bJEu (к'у) к'у 0                _

—

1          ^к ' у

Л<у) J Ep(')de]' =

h                                                 h

= 2bJEu (к'у)(к0 + dк)у2dy — 2bJ

к₀ у             к' у

J E p de + J E p de

⁰          к у

ydy .

Получим линейное приближение уравнения (17). Для этого сначала разложим функцию E u ( к ' ) в ряд

Тейлора в точке равновесия и возьмем первый член, равный E0u . Затем разложим интеграл с переменным верхним пределом к'у в последнем слагаемом выражения (18). Так как первый член этого разложения равен нулю, то используем второй (линейный) член, равный E0dку. Тогда уравнение (17) в линейном приближении

h

имеет

вид

^к 0 у

к0 + dк = (M0 + dM)/ JU + (Mф (к0) + Mф (dк))/J0 , h

где

M ^ф ( к ₀ ) = 2 b J E u к ₀ у — J E p de ydy , M ^ф ( d к ) = 2 b ■ d к J ( E u — E ₀ p ) у ² dy = d к ( J u — 2 bJ ₀ p ) , точка ( к ₀, M ₀ ) —

точка равновесия. Следовательно к ₀ = ( M ₀ + M ^ф ( к ₀ ))/ J U . Таким образом, окончательно запишем d к = dM/J U + d к ( 1 — 2 bJ ₀ p/ J 0 ) , J U * 0, или

2 bJ ₀ p d к = dM . (19)

Уравнение (19) имеет единственное решение, если J0p * 0, причем малому приращению dM > 0 отвечает малое же приращение dк, то есть решение устойчиво (задача корректна по Адамару [15]). Однако здесь следует различать два случая. В первом случае J0p > 0 и величина dк > 0 . Тогда при малом догружении балки с тангенциальной жесткостью J0p кривизна возрастает также на малую величину (исследуемое положение равновесия устойчиво). Во втором случае, когда J0 < 0, из уравнения (19) находим, что dк< 0. Следовательно, после догружения балки равновесие возможно, если уменьшится её кривизна, то есть балка распрямится. Но такое поведение противоречит закону сохранения энергии [16], и равновесие не может существовать. Таким образом, равновесие балки при условии J0 < 0 имеет неустойчивый характер. Кроме того, на неустойчивость указывает и то, что П кк < 0, когда J0 < 0, то есть потенциальная функция П выпукла вверх и имеет в каждой точке локальный максимум. Наконец, если J0 = 0, то любому малому приращению dM отвечает бесконечное увеличение кривизны (задача некорректна по Адамару). Отсюда исходное уравнение равновесия неустойчиво.

В случае упругопластического материала исследование устойчивости по линейному приближению проводится аналогично. Разница лишь в том, что J U = 2 bh³E /3 = const. При J 0 < 0 равновесие также неустойчиво.

Когда материал упругохрупкий, то Mф = 0 и уравнение (17) принимает вид к' = M’M (к').

Разлагая функцию E s ( к ' ) в ряд Тейлора, имеем

Es (к') = Es (к)+ dE-d к

d к + ... .

^к = ^к 0

„      dEs   dEs de   d Г ст) de ст)-e-ст     EP - Es     EP - Es

В разложении (21) берем два

Здесь ---=--= —I —I— = ——2-- y =-- y =-----

• d к   de d к deye) d к     e           кyк

9.    Локализация деформаций

первых члена, так как секущий модуль принципиально не может оставаться постоянным при догружении.

Тогда    Js = 2 bhEs (к' y) y2 dy =2 bhEsy2 dy + 2b d к J (E0P - E0s) y2 dy = Js +(2 bJ0 /к0) d к-( JО/к0) d к,и о                      0            к00

уравнение (20) преобразуется в равенство к ₀ + d к = ( M ₀ + dM ) ( J s + ( 2 bJ 0 /к ₀ ) d к- ( J 0 /к ₀ ) d к ) , или к ₀ J s + J 0 d к + 2 bJ 0 d к + ( 2 bJ 0 /к₀ ) d к ² - J s d к - ( J 0 /к₀ ) d к ² = M ₀ + dM . Пренебрегая квадратичными членами и учитывая, что в силу равновесия исходного состояния J 0 ^s к ₀ = M ₀, окончательно получаем линейное приближение к уравнению возмущенного равновесия, которое совпадает с уравнением (19). Следовательно, результаты анализа устойчивости, приведенные выше, справедливы и для балки из упругохрупкого материала.

Отметим, что анализ устойчивости по линейному приближению идентичен исследованию устойчивости, проведенному методами теории катастроф (раздел 7).

Остановимся ещё на случае, когда возмущение равновесия балки происходит посредством задания малого приращения кривизны d к = 0 (жесткое догружение). Если величина J 0 ограничена, то, подставляя d к> 0 в равенство (19), однозначно определяем величину dM . При этом малому значению d к соответствует малое же значение dM (задача корректна по Адамару). В отличие от мягкого догружения, задание параметра d к> 0 уже жестко фиксирует некоторое положение равновесия, и величина dM принимает значение, отвечающее этому равновесному состоянию. Поэтому балка сохраняет равновесие и при J 0 >  0 в случае dM >  0 (разупрочнение). Равновесие нарушается, если J 0 = -от , то есть диаграмма деформирования материала имеет вертикальную падающую ветвь (неустранимая неустойчивость материала).

Если балка изготовлена из партипластического или упругопластического материала, то возмутить положение равновесия возможно, задав приращение пластических деформаций d e ⁰ ( y ) . Тогда уравнение возмущенного равновесия в линейном приближении принимает вид J 0 d к = 0 (в выражении (19) величина dM = 0). Очевидно, что при J 0 ^ 0 данное уравнение имеет только тривиальное решение. Когда J 0 = 0 , то решений бесконечно много, и, следовательно, возмущение равновесия подобным образом приводит, по крайней мере, к конечному возрастанию кривизны, то есть к потере устойчивости равновесного состояния. В силу естественного разброса свойств по длине балки величина J ₀ ^p впервые достигает нуля в одном из её сечений; и в этом сечении возмущение посредством приращения пластических деформаций приводит к практически неограниченному возрастанию кривизны.

Аналогичный вывод можно сделать для балки из упругохрупкого материала, исходя из анализа устойчивости по линейному приближению. Только возмущение в этом случае следует производить посредством малого приращения величины J^s . Если при равновесии балки в каком-либо сечении величина J ₀ ^p обратится в нуль, то любое возмущение параметров внутреннего состояния приводит к локализации деформаций в этом сечении.

10.    Заключение

На примере чистого изгиба балки прямоугольного сечения, изготовленной из материала, имеющего диаграмму деформирования с падающей ветвью, показана возможность и дана методика применения итерационных методов решения нелинейных уравнений, которые описывают напряженно-деформированное состояние тел с разупрочняющимися элементами. Использован метод простой итерации для определения параметров устойчивых положений равновесия и метод Ньютона–Канторовича, позволяющий найти параметры системы для всевозможных равновесий, в том числе и неустойчивых. Кроме того, продемонстрировано, как специальные математические методы исследования устойчивости механических систем (методы теории катастроф, теории особенностей дифференцируемых отображений, метод исследования устойчивости по линейному приближению) могут быть приложены к определению устойчивости процесса деформирования тел из разупрочняющегося материала.

Работа выполнена при финансовой поддержке РФФИ (проекты № 10-01-96018-р_Урал_а и 10-08-00135).