Математические модели центров равнодавлений в звездных системах
Автор: Гуревич Г.С., Лутманов С.В., Пенский О.Г.
Журнал: Вестник Пермского университета. Математика. Механика. Информатика @vestnik-psu-mmi
Рубрика: Механика
Статья в выпуске: 3 (54), 2021 года.
Бесплатный доступ
Предлагаются математические модели, позволяющие вычислять координаты центров равнодавлений в звездных системах и решать обратную задачу определения источников излучения материальной субстанции при формировании макротел. Показывается не единственность решения прямой и обратной задач.
Математическая модель, звездная система, центр равнодавлений, сила, давление
Короткий адрес: https://sciup.org/147245521
IDR: 147245521 | УДК: 530.12:531.551 | DOI: 10.17072/1993-0550-2021-3-25-30
Текст научной статьи Математические модели центров равнодавлений в звездных системах
Звезды в галактике, излучая материальную субстанцию, образуют центры равнодав-лений, в которых рождаются макротела.
В работе [1] дано следующее определение центра равнодавления: "Центр равнодав-ления – это точка в пространстве, где равнодействующая сил, порожденная давлением материальной субстанции, излучаемой другими точками (звездами), равна нулю".
Принцип формирования центров равно-давлений звездами в интервале 5, 10 и 15 световых лет показан на рисунке.
В работах [2–4] исследован процесс образования центров равнодавления и приведены иллюстрации образования центров равно-давлений в звездных системах.
В статье [5] приведен пример, показывающий, что центров равнодавлений в одной и той же звездной системе может быть несколько.
В настоящей статье предлагаются математические модели, позволяющие вычислять координаты центров равнодавлений в звездных системах, исходя из известных координат излучающих материальную субстанцию звезд (прямая задача), а также описан способ вычисления координат излучающих материальную субстанцию звезд, исходя из известных координат центра равнодавления (обратная задача).
Заметим, что существует множество систем координат, позволяющих описывать расположение макротел во Вселенной [6].
В дальнейшем для простоты математической формализации мы будем использовать декартову систему координат с центром координат аналогичным эклиптической системе [7].
Использование декартовой системы нисколько не умаляет общность решаемых ниже задач, так как существующие координаты звезд легко переводятся из одной системы координат в другую.
ПРОСТРАНСТВЕННОЕ РАСПОЛОЖЕНИЕ ЗВЁЗД В ИНТЕРВАЛЕ 5,10 И 15 СВЕТОВЫХ ЛЕТ
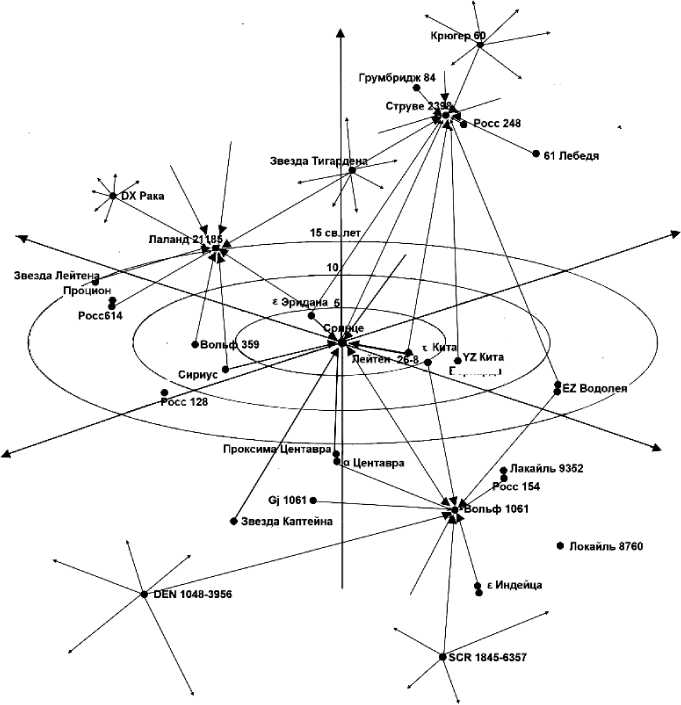
Бернарда
Обозначения
к , • • •, кт е R 1 — коэффициенты пропорцио-
Введем следующие обозначения.
Пусть
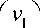
v = V2
V v3 )
е R3 -
центр равнодавления (центр);
нальности;
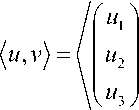
v 2
( v ^
V v3 J
=Z uv i=1
—
символ ска-
лярного произведения векторов u , v е R 3;
II u — v|l = V (u — v, u — v
Z ( u— rf
= 1
—
P о R 3 — область возможного положения центра;
норма разности векторов u , v е R 3;
IIF (v )||= ^ 2,i'MV", "} — v — u
величина
силы, действующая со стороны i — го источника на точку, находящуюся в центре v е R 3;
e i ( v ) = II v ^11 ’ i e{ 1’’”’ m } —
Iv -u II вектор, направленный от i — го центру v g R3;
единичный источника к
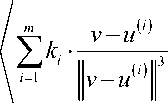
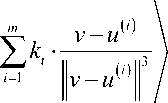
^ min,
u G P o R 3.
F ( v ) = l I F ( v )|| - e i ( v ) = I
1 (i)( k v—u
-----i—- • 7-----— = k.--. i
II v — u^\2 |v — u“| i |v — u "f
-, m } -
вектор силы со стороны i — го источника, действующей на точку, помещенную в центр v g R 3;
Нулевое значение целевой функции на оптимальном векторе v0 g R3 будет означать, что прямая задача решена и вектор v0 g R3 представляет собой радиус-вектор искомого центра. Заметим, что в случае отсутствия ограничений, т. е. когда P = R3, у задачи все гда имеется решение v0 = ^
mm
F ( v ) = E F i ( v ) = E k i • i = 1 i = 1
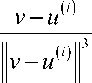
—
вектор равнодействующей всех сил со стороны источников, приложенных к точке, помещенной в центр v g R 3.
Прямая задача (задача 1)
Пример 1
Дано:
( 1 '
m = 4, u ( 1 ) = 0
0 k о J
( 1 Л
( 0 Л
( о Л
Дано:
и ( 1 )- u
Л (1)Л u1
u ( 1 )
u ( 1 ) k 3 J
g R 3,---, u(m ) —
, ,F= 1
, u '”= 0
k о J
k 1 J
, u ( 4 ) = 1 , k 1 = k 2 = k 3 = k 4 = 1 ,
k 1 J
P Ч
Хг , X 2, X 3 G
, ,
( m ) ui
u
u k -
' ( m )
, ( m )
3 J
g r 3, v-
k m G R 1 , P О R 3 .
v 1
x
Вектор равнодействующей записывается в виде
F ( v ) = E F i ( v ) = E k i'
Найти центр v 0
v 2 0
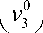
G P
( i ) v — u ’
I v — u ( i )|
v =
из условия
равенства нулю равнодействующей F ( v ) .
Целевая функция имеет вид
All2 _ / V v — ui V v — ui
I v — ui lf’ i =1 l v — u-|3
x 1
k x 3 J
.
.
Решение:
Вектор v0 g R 3 будем искать как решение следующей задачи математического программирования на условный экстремум:
mm
II F ( v )ll =te F ( v ) • E F ( v )) =
\ i — 1 i = 1 /
Пример решался в среде пакета "Mathe-matica".
Для решения задачи математического программирования применялась команда
NMinimize[{ F [x1,x2,x3],-1 Результаты расчетов: {2.90892*10Л-30, {x1 -> 0.5, x2 -> 0.5, x3 -> 0.5}}. Как видно из приведенных расчетов, значение целевой функции в найденной точке mm IF ( v ” )| — ZF ( v" ),ZF( v ”) — i=1 i=1 v0 ' 0.5 ' 0.5 . 0.5, равно 2.90892 x10 30, т. е прак- m ZV i—1 0 (i) v — w’ I v0 — и(‘) m p Z V i —1 v0 — и 1) \ . ------- ^ min, Iv0 — U «I тически ноль. Следовательно, точка v0 Л0.5 ^ 0.5 совпадающей с целевой функцией прямой задачи. Однако здесь ее переменными явля- является искомым центром. 0.5 ются Обратная задача (задача 2) Используя обозначения предыдущего пункта, сформулируем задачу, обратную к задаче 1. Дано: и (1) -и (и u ( (—) А U и (’) u ,-, и-) — (—) U (1) и (—) U V 3J V 3J , а пара- v v v0 v v € R3, k,•••,km € R\ p c R3, i e{1,---,—}. Найти: (1) и\7 u (1) = и u u V - •S’ -(1) 3J п (—) € P,---,U 1 — для которых mm F (v 0) —Z F (v 0) —Z kr метры v0 v v € R3считаются известными. Ограничения на переменные имеют вид и (1) = и— (—) U1 u u V < m ■ 3-)J € Pm , 0 (i) v — w} I v0 — u 2 ‘) я — 0. Здесь p c R3, i €{1, • • •, —} — области предположительного расположения источников. Очевидно, что если допустить свободное расположение источников во всем пространстве R3, то задача 2 будет иметь бесконечно много легко строящихся решений. Решение: Вектора U1 ( (—) A U1 и (1) -и u u v ■ '(1) 3J (—) € P,---,U ’ — u u V ' 2m) , (m) '3 J GPm будем искать как решение задачи математического программирования на условный экстремум, с целевой функцией U1 (—) U1 u u V '(1) ' (1)'3 J (—) € P,---,U 1 — u u V , 2-) ■ 3■) € P— - Задача 2 считается решенной, если оптимальное значение целевой функции равно нулю. Пример 2 Дано: v0 Л0.5 0.5 €R3, p,---,P4 cR3, . 0.5, U11 P — ’ U12 (U1 P2—^ p 4 — 1)2 + (и» )2 +(U13 )2 < 14, V U13 J u21 u22 u ( U 21 ) +( U 22 — u31 u32 u (U31 )2 +(U32 )2 +(U33 — ( u 41 - 1) +(u42 - 1) +(u43 - 1) - 12 ’ Представляет интерес решение прямой задачи, в которой положение источников определяется векторами _ (10) (20) (30) (40) _ u ,u , u ,u , найденными как реше- Вектор равнодействующей записывает- а множество ся в виде F (v0) = Z k. i—1 0 (i) v — u I v 0 — u «IГ ние обратной задачи, совпадает с u 0 = u ( ah u( ) f (4 h u1 u (1) u2 u (4) — U (4) u2 u У к 3 7 u 54) к 3 7 Целевая функция имеет вид Пример решался в среде пакета "Mathe-matica". ограничениями исходной задачи 1. Результаты расчетов: {1.51618*10^-20, {x1 -> 0.500006, x2 -> 0.500002, x3 -> 0.5}}. Как видно из расчетов, значение целевой функции в найденной точке (0.500006 v0 — 0.500002 0.5 Для решения задачи математического программирования применялась команда NMini- mize[{F[u11,u12,u13,u21,u22,u23,u31,u32,u33,u 41,u42,u43] равно 1.51618х10 20 , т. е. практически ноль. Легко видеть, что имеет место совпадение полученных координат центра с теми, которые были вычислены при решении исходной прямой задачи в примере 1. Результаты расчетов: {3.62867*10^-16, {u11 -> 1.17403, u12 -> 0.102601, u13 -> 0.556784, u21 -> -0.571177, u22 -> 0.885622, u23 -> 0.786926, u31 -> 0.14806, u32 -> -0.411013, u33 -> 0.401974, u41 -> 0.321408, u42 -> 1.26398, u43 -> 0.405633}}. Как видно из расчетов, значение целе- вой функции в найденных точках ^ 1.17403 Л ' —0.571177^ и (10) -u — 0.102601 , u(20) — 0.885622 , к0.556784J к 0.786926 7 ^ 0.14806 Л " 0.321408^ u(30) — —0.411013 . u(40) — 1.26398 к0.401974 J к 0.405633J равно 3.62867 х10 16 3.62867*10Л-16, т. е практически ноль. Следовательно, точки (10) (20) (30) (40) u ,u ,u u являются искомыми источниками. Найденные точки не совпадают с теми, которые фигурировали в условиях прямой задачи примера 1. Отсюда следует не единственность решения обратной задачи. Заключение Таким образом, в настоящей статье впервые предложены математические модели, позволяющие решать прямую и обратную задачи определения координат центров равно-давлений и источников формирования центров равнодавлений. Другие группы звезд образуют другие центры равнодавлений. Звезды могут входить одновременно в другие группы звезд, образуя другие центры равнодавлений.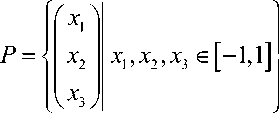
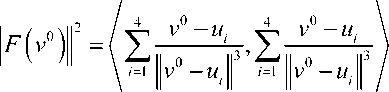
Список литературы Математические модели центров равнодавлений в звездных системах
- Гуревич Г.С. Математическое моделирование процессов в гравитационном поле макротел // Вестник Пермского университета. Математика. Механика. Информатика. 2021. Вып.1(52). С.16-24. EDN: RMITCB
- Гуревич Г.С., Каневский С.Н. Материя, пространство, время, гравитация. М.: ИПО "У Никитских ворот", 2009. 248 с. 978-5- 91366-112-8. ISBN: 978-5-91366-112-8 EDN: QJWBQZ
- Гуревич Г.С., Каневский С.Н. Чем Солнце тянет Землю? М.: ИПО "У Никитских ворот", 2012. 72 с. ISBN: 978-5-91366-376-4 EDN: QJZJBJ
- Каневский С.Н., Гуревич Г.С. Астродинамика М.: ИПО "У Никитских ворот", 2009. 384-с. ISBN: 978-5-91366-081-7
- Гуревич Г.С., Пенский О.Г. О существовании центров равнодавлений, являющихся центрами концентрации материальной субстанции // Вестник Пермского университета. Математика. Механика. Информатика. 2021. Вып. 2(53). С. 25-28. DOI: 10.17072/1993-0550-2021-2-25-28 EDN: FUIBMA
- Серапинас Б.Б. Геодезические основы карт. URL: http://www.geogr.msu.ru/cafedra/karta/docs/GOK/gok_lecture_2.pdf (дата обращения 16.06.2021).
- Эклиптическая система координат. URL: https://vuzlit.ru/511614/eklipticheskaya_sistema_koordinat (дата обращения 16.06.2021).


