Математические модели дрейфа функциональных параметров электронных изделий

Представляется очевидным, что разработка универсальных моделей оценки деградации функционального качества должна идти по пути использования достаточно общих (фундаментальных) физических закономерностей и представлений. В этой связи уместно отметить, что любые технические устройства являются по своей физической сути существенно неравновесными системами, поэтому наиболее корректная постановка вопроса предполагает, что методологической основой универсальных методов должен быть теоретический аппарат неравновесной термодинамики и статистической физики. Однако этот путь решения вопроса представляется весьма проблематичным, если учесть современное состояние указанных теоретических разделов и трудности, возникающие при определении взаимосвязи между техническими параметрами устройств, представляющими практический интерес, и физическими параметрами, которыми оперирует теория неравновесных систем. Последнее обстоятельство обусловливает правомерность рассмотрения представленной проблемы в рамках формализованных (полу-эмперических) подходов, использующих в своей основе ряд основополагающих физических гипотез [1].

Цель данной работы: построение достаточно универсальных моделей деградации технических параметров.

В настоящей работе в качестве исходного принципа построения моделей принято энергетическое представление процессов деградаций, а в качестве методологической базы – основополагающие идеи теории физической надежности. Рассматриваемые модели относятся к случаю частичной потери функционального качества элементов конструкции КА (непрерывных отказов) и предусматривает два подхода: детерминированный и вероятностно-детерминированный. Отличие оговоренных подходов состоит в том, что возмущающие факторы в первом случае считаются заданными точным образом, а во втором - рассматриваются как случайные величины, заданные своими вероятностными характеристиками.

Детерминированная модель расходования ресурса. В соответствии с распространенной практикой примем, что текущее со- стояние элемента определяется совокупностью функциональных параметров {Пi}, полностью определяющих потребительское качество элемента. В процессе эксплуатации элемента допускаются изменения параметров {Ani0}, не приводящие к потере функционального качества. Функциональное качество элемента вы- ражается в относительных единицах в виде

V/ отношения —г-, где П, - начальное значение

П”          i функционального параметра (в дальнейшем -параметра) при t=0 с, а Ani - отклонение от начального значения параметра в текущий момент времени. Исходя из общих кинетических закономерностей развития элементарных (атомных) процессов [2, 3] можно заключить, что скорость деградации (старения) элементов определяется двумя моментами:

• -    спецификой протекания элементарных процессов, приводящих к изменению начальной атомной структуры элементов;

• -    интенсивностью возмущающих факторов, оказывающих воздействие на элемент.

В этой связи изменение параметров элемента следует рассматривать как результат последовательного накопления нарушений начальной структуры элемента на атомном уровне под воздействием возмущающих факторов (предполагается, что появление функционального качества у некоторой совокупности атомов связано с их предварительным упорядочиванием в определенную структуру). Устойчивость функционального качества элемента можно сопоставить с устойчивостью первоначальной (искусственно созданной неравновесной) атомной конфигурации элемента. Последнюю можно оценить на основании извест- ных энергетических характеристик, а именно, энергетического потенциального барьера элементарных процессов.

Сформулированные в [1] гипотезы составляют основу энергетического подхода рассмотрения вопросов деградации элементов.

Физической сутью оговоренных гипотез является представление об уменьшении начального энергетического барьера W_0i в результате воздействия возмущающих факторов [4]. Примем, что начальное качество элемента характеризуется значением параметра П ₀ (здесь и далее рассматривается однопараметрический случай, поэтому индекс i опускается), обусловленного определенной атомной структурой элемента. В процессе эксплуатации элемента значение параметра П будет изменяться, причем в тем большей степени, чем выше интенсивность протекающих элементарных атомных процессов, определяющих качество элемента по параметру П . В соответствии с [5] было использовано понятие обобщенной глубины х протекания элементарных атомных процессов:

c - с0 x =---- c9                        (1)

где с , с ₀ - соответственно, текущая и начальная концентрация активных центров атомной структуры.

Под активными центрами понимаются атомные конфигурации, способные к трансформациям различного рода (диффузионным, химическим, структурным и т.д.). Представляется очевидным, что:

П = Ф ( х )               (2)

В подавляющем большинстве случаев, встречающихся в практике создания электронных устройств, прогнозирование ожидаемого ресурса элементов связано с анализом достаточно малых отклонений A П , а следовательно и А х . Заметим, что в начальный момент времени, согласно (1), x =0, поэтому, разлагая функцию ф ( х ) в степенной ряд в окрестности значений x =0, в первом приближении имеем:

П = П ₀ + Ах     (3)

Аналогичным образом, для самой величины x имеем:

х = kt             (4)

где t - продолжительность функционирования элемента; k - константа скорости протекания процессов деградации элемента по параметру П .

Модель потенциального энергетического барьера определяет вид константы k в следующей форме:

- W k = k 0 e kt

где k 0 – константа, характеризующая скорость процесса при T -^ ^к ; W - энергия активации процессов деградации элемента по параметру П ; k – постоянная Больцмана; T - абсолютная температура.

С учетом вышеизложенного имеем:

л ГТ        - W

А П ---= Bte ^kT

П 0

В выражении (6) совокупность возмущающих факторов представлена в неявном виде (кроме температуры). В результате получаем три модели расходования ресурса.

Модель №1:

оговоренной в наименовании раздела , настоя щее рассмотрение преследует и дополнитель ную цель , а именно , изыскание возможности минимизации объемов экспериментальных ис следований . Учитывая высокую себестоимость и трудоемкость экспериментальных исследо ваний , последнее обстоятельство представляет определенный практический интерес . Для оп ределения начальной энергии активации W 0 обеспечим следующие условия испытаний : Q j =0. В этом случае выражение (7) приобрета ет вид :

А П

П 0

— W o

= Bte ^kT

—I

А П  _D

---= Bte

П 0

Wo+2 qjQj j kT

Модель №2:

Проведем исследование величины Δ П при различных температурах T 1 и T 2 . Выбор диапазона возможных температурных изменений подчинен условию сохранения механизма деградации элементов:

—

А П  „

---= Bte

П 0

j * ^k

- 2 qj,tQjQt j,k kT

АП_{Х D} ^r¹ = Bt j e

П 0

Модель №3:

А П 2

П 0

АП  n

---= Bte

Wo +2 qjQj + 2"q, kQjQk j                j,k kT

— W ) kT 1

- W o

= Bt 2 e^k T

На основании выражения (11) имеем:

ln

П 0

W 0

= k

^{t2 А П}_L "  1 1 1 А П ₂ J

Модель № 1 (7) справедлива для случая взаимно - независимого влияния индивидуаль ных возмущающих факторов КП на изменение параметра П в процессе эксплуатации элемен та . В противном случае справедливы модель № 2 и № 3.

Методика определения параметров детерминированной модели расходования ресурса. Определение параметров модели дегра дации технических параметров производится с помощью натурных моделирующих экспери ментальных исследований . Для проведения исследований берется партия элементов и принимается , что в пределах выбранной пар тии элементы являются идентичными с точки зрения их начальных параметров П 0 и процес сов деградации под воздействием возмущаю щих факторов . В целях упрощения определе ние параметров производилась на примере мо дели расходования ресурса № 1. Распростране ние полученных результатов на другие модели расходования ресурса не вызывают принципи альных трудностей . Наряду с основной целью ,

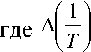
T

T ₂

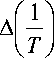
T 1

Если Δ П 1 = Δ П 2 , то выражение (12) упрощается:

W 0

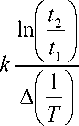
Выражения (12) и (13) определяют начальную энергию активации W 0 по результатам двух экспериментов, проведенных при различных температурах T 1 и T 2 . Для определения коэффициентов чувствительности к возмущающим факторам q j обеспечим следующие условия испытаний:

Q j

<

0, npuj = 1

Q l 1 , ^Q l 2 при = l

где Q l1 и Q l2 – интенсивности возмущающего фактора Q l (значения Q l1 и Q l2 выбираются в интервале значений, представляющих практический интерес).

По результатам испытания элементов при значениях возмущающего параметра Q l1 и Q l2 имеем:

ап/  n_t  J W + qQ

1                                           0 l l 1

/n 0 = Bt 1 exp t          /т т j

^{A n}2/ =    exo/-( ^W о ^{+ qQ l} 2 )/ I

/n 0 Bt ² exp t           /т т j

На основании выражения (14) имеем:

ql

= TT In

А П 1 t 2/

/^ 2 t 1

А Ql где ΔQl = Ql2 – Ql1.

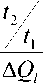
Если Δ П 1 = Δ П 2 , то (15) упрощается:

ql

= TT In

к 7

Выражения (15) и (16) определяют коэффициент чувствительности q l по результатом двух экспериментов, проведенных при одинаковых температурах, но при двух различных интенсивностях возмущающего фактора Q l . Определение множителя B не требует постановки специальных экспериментов. Для его определения воспользуемся следующим выражением:

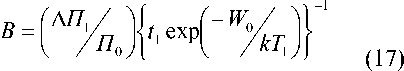
Общий объем экспериментальных исследований, необходимых для определения полной совокупности параметров детерминированной модели, можно определить по выражению: n э = 2( n + 1), где n – общее количество возмущающих факторов. Для определения режимов ускоренных моделирующих испытаний можно воспользоваться следующей формулой:

t у = t р ^eX P ‘

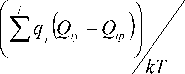
j где tу и tp – продолжительность ускоренных и реальных испытаний; Qiy и Qiр – интенсивность возмущающего фактора в режиме ускоренных и реальных (нормальных) испытаний соответственно.

В практических приложениях может представлять интерес и обратная постановка вопроса, а именно, определение уровней Q у для наперед заданной величины C=t у /t р . В этом случае, для однофакторного возмущения имеем:

Tt In C + qP„

P =------

Py q                (19)

Используя приближение Р р ≈0 получим:

kt ln C

Py = q                   (20)

В ряде случаев может представлять интерес преставление вышеизложенных результатов в относительном (безразмерном) виде. Это позволит провести сравнительную оценку повреждающего воздействия различных возмущающих факторов. На основании выражения (19) имеем:

^Py - P_p = Tt In C

P p  ⁼ I P T

Вероятностно-детерминированная модель. Детерминированный подход предполагает, что характеристические параметры модели деградации технического устройства ( B , W 0 , q i ) заданы точным образом. В более корректной постановке вопроса указанные параметры следует рассматривать, как случайные величины, заданные своими вероятностными характеристиками. В этой связи уместно дополнить рассмотренную детерминированную модель вероятностным представлением характеристических параметров. Последнее составляет основу вероятностно-детерминированной модели расходования ресурса. Эффективность вероятностно-детерминированного подхода определяется степенью достоверности используемых вероятностных характеристик, в частности математического ожидания и дисперсии случай- ^^^

ных величин B , W 0 , q i вида и значений параметров совместного закона распределения этих величин. На данном этапе рассмотрения вид совместного распределения переменных выбирается не на основании опытных данных, а априорно постулируется. С учетом привлечения вероятностных представлений основополагающее выражение (модель №1) приобретает вид:

—— = t • B • exp⁽ - ⁽ W о + X q , ■ Q i )/ ^k • T )•

Пi

Конечной целью    вероятностно- детерминированного подхода является определение вероятностных характеристик пара- дисперсии для любого момента времени эксплуатации элемента. Плотность распределения

A ю (у) параметра —— может быть представлена

П в следующем виде:

Гоу = B1 • j e u2 f (у, u) du

-”                      (27)

где

— — метра ——, а именно математического ожидания my, дисперсии ay2, плотности распределения ю(у). Представление характеристических параметров модели в виде случайных величин позволяет также перейти к исследованию еще одной важной в технических приложениях величины - времени работы элемента до возникновения постепенного отказа (уход A

—— за допустимые пределы). В последнем П случае оказывается возможным сформулировать разумные ограничения на пределы изме-

B1 =

— exp

x

f 1 ⁽ у , ^u ) = ^exP^{{ -}

(-

V

2 .                2 A

m + 2 • m • ст x    zx

r^[ 2 • a_;c

2 • ax     J

(28) A2

ua ₇ V2 + m ₇ e ^{z z} J

+

+ 2 y • m z   + 2V2 • u • o_z • a ²]}.

un,V2+m,                       z x e z z

нения случайных величин в , W , q . , обеспечивающие необходимую вероятность безотказной работы элемента. Математическое

— II ожидание my параметра -—— с учетом ранее проведенных преобразований [6,7] имеет следующий вид:

На основании плотности распределения го(у) можно получить вероятность нахождения

параметра у в наперед заданном интервале

значений (у₁,'у₂) :

у 1

P(У1 < у < у2) = j ^(у)dy у 1

где

mz

a

m_y = t m x exp [(2 m z + a z ² )/2] (23)

V

A

( M W о

A

A

+ X ^M q i • Q i )/ ^kT ;

i

Практическое использование полученных результатов предполагает апробацию гипотезы о нормальном законе распределения A A величин x и z . Для оценки плотности распределения времени безотказной работы элемента была получена следующая формула:

D W о + X Q , ²• D q.

i

A ПА

J?

•(k • T)- 2.

от

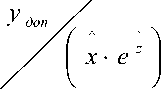
Для определения дисперсии а у ² параметра ^{— —}

П было получено следующее выражение:

„2    ,2 2 m+7 ?1 2 а 2    ,„„2/ а 2

о, = t e z z ae z + mv(e z -1) y    xx

Полученное выражение позволяет провести анализ причин, обусловливающих рас-A сеяние ——, а также вычислить значение П где tom - случайная величина, характеризующая время безотказной работы элемента.

Выводы:

• 1.    Представлена методология применения термоактивационного подхода при анализе процессов деградации функциональных параметров изделия.

• 2.    Построена детерминированная модель расходования ресурса элементов электронного устройства по критериям функционального качества. Основные результаты детерминированной модели деградации технических параметров

• 3.    Получены аналитические выражения, определяющие плотность распределения времени безотказной работы изделия в условиях воздействия возмущающих факторов.

распространены на вероятностно-детерминированный случай, предполагающий задание характеристических параметров в виде случайных функций. Для указанного подхода рассмотрения функционального качества элемента определены вероятностные характеристики (математическое ожидание, дисперсия, плотность распределения).