Математические модели энергодвигательного комплекса системы транспортно-технического обеспечения для развертывания и обслуживания орбитальной группировки космических аппаратов
Автор: Евдокимов Роман Александрович, Фадеев Александр Сергеевич
Журнал: Космическая техника и технологии @ktt-energia
Статья в выпуске: 2 (2), 2013 года.
Бесплатный доступ
Рассмотрена совокупность математических моделей, необходимая для формализации задачи параметрического синтеза энергодвигательного комплекса системы транспортно-технического обеспечения орбитальной группировки космических аппаратов. Представлена классификация математических моделей энергодвигательных комплексов и их наиболее характерные примеры. Использование разработанных моделей позволяет формализовать и решить задачу оптимизации проектных параметров энергодвигательных комплексов системы транспортно-технического обеспечения с учетом неопределенности исходной информации.
Математическая модель, энергодвигательный комплекс, техническое обслуживание, межорбитальная транспортировка, стохастическая модель
Короткий адрес: https://sciup.org/14343415
IDR: 14343415 | УДК: 629.78.01:519.872.6
Текст научной статьи Математические модели энергодвигательного комплекса системы транспортно-технического обеспечения для развертывания и обслуживания орбитальной группировки космических аппаратов
ЕВДОКИМОВ Р.А.
ЕВДОКИМОВ Роман Александрович – ктн, начальник сектора
EVDOKIMOV Roman Alexandrovich – Candidate of Science (Engineering), Head of Sector at RSC Energia

ФАДЕЕВ А.С.
FADEEV Alexander Sergeevich – Candidate of Science (Engineering), General
Director of the FGUP TsNKI
Одним из возможных и перспективных путей снижения материальных затрат на развертывание и обеспечение высокого уровня технической готовности обширных орбитальных группировок космических аппаратов (КА), размещаемых на высоких орбитах, является создание систем транспортно-технического обеспечения орбитальной группировки (ОГ) [1]. Под системой транспортно-технического обеспечения (СТТО) понимается совокупность КА, предназначенных для развертывания ОГ (выведения КА c опорной на рабочие орбиты), а также ее дальнейшего технического обслуживания (ТО) – замены вышедших из строя элементов бортовых систем КА и дозаправки компонентами топлива их двигательных установок коррекции (ДК) и ориентации (ДО).
Один из наиболее общих и сложных случаев построения СТТО предусматривает включение в ее состав многоразовых межорбитальных буксиров (МБ) с жидкостными ракетными двигателями (ЖРД) большой тяги для развертывания ОГ в приемлемые сроки, а также космических аппаратов обслуживания (КАО) с солнечными электроракетными двигательными установками (СЭРДУ) [1]. КАО фактически являются многоразовыми межорбитальными буксирами, оснащенными робототехническим комплексом (РТК) для ремонта и дозаправки КА ОГ. В работе [1], где рассматривается подобная система, принято, что МБ и КАО дозаправляются и проходят техническое обслуживание на орбитальном космическом центре (ОКЦ) – орбитальной пилотируемой станции, оснащенной системами хранения и дозаправки топливом транспортных КА.
В работах [1, 2] показано, что для систем, подобных СТТО, на ранних этапах проектирования актуальна задача оптимизации проектных параметров энергодвигательного комплекса (ЭДК), представляющего собой совокупность энергодвигательных систем (ЭДС) КА, входящих в СТТО, связанных выполнением единой задачи. Под ЭДС понимается комплекс бортовых систем, от степени совершенства которых в первую очередь зависит эффективность выполнения КА целевых задач [2–4]. В состав ЭДС обычно включают системы энергопитания, терморегулирования, хранения и подачи топлива, а также активные исполнительные органы систем управления движением и ориентации. В ряде случаев (для пилотируемых КА) в ЭДС включают также систему жизнеобеспечения (СЖО) [4].
Учитывая, что СТТО является ярким примером сложной технической системы, функционирующей в условиях неопределенности (в частности, априори стохастическим, т.е. случайным, является поток отказов систем КА ОГ), для решения задачи параметрического синтеза ЭДК СТТО целесообразно воспользоваться методологией комплексной оптимизации энергодвигательных систем КА, предложенной в работах [2, 3]. В соответствии с данной методологией показателем качества ЭДК СТТО является вероятность выполнения им своей задачи – P ВЗ . Использование данного показателя эффективности позволяет адекватно учесть неопределенность условий применения и функционирования ЭДК СТТО. Вероятность выполнения задачи (ВВЗ) фактически представляет собой вероятность выполнения совокупности стохастических неравенств, описывающих требования к ЭДК СТТО. Левые части неравенств описывают достижимые результаты функционирования ЭДК, а правые – требуемые [1–3].
В общем виде задача формулируется следующим образом [1].
Заданы структура и условия применения орбитальной группировки КА, состав, параметры и технические характеристики бортовых систем КА ОГ. Известны законы распределения случайных величин, характеризующих требования к системам КА орбитальной группировки, выбраны состав СТТО и структура ЭДС МБ, КАО и ОКЦ, фиксированы способ развертывания ОГ, стратегия и степень технического обслуживания, кратность применения МБ.
Необходимо определить значения проектных параметров ЭДК СТТО, которым соответствует максимальное значение вероятности выполнения задачи ЭДК P ВЗ при соблюдении ограничений на суммарные массовые затраты и на управляющие параметры (проектные параметры ЭДК).
Математическая формулировка задачи выглядит следующим образом:
Х<т> ~ ^А^е^'}™3^
X® > = К >: и(х< >)}; ■ <т> 1 <т> х <т>71 ’ х <т>/ L фJ доп J
Здесь х<, – вектор оптимальных значений управляющих параметров;
X
Формализация задачи синтеза ЭДК СТТО начинается с анализа требований к ЭДК [1], позволяющего сформулировать условия выполнения задачи ЭДК заданной структуры в виде системы неравенств. Выполняется анализ системы с целью выявления стохастических неравенств для формализации показателя эффективности.
Для получения функциональной зависимости показателя эффективности – ВВЗ от проектных параметров ЭДК (управляющих параметров решаемой оптимизационной задачи), а также от характеристик условий применения и функционирования, необходимо найти законы распределения всех случайных величин, фигурирующих в стохастических неравенствах, а также получить зависимости параметров законов распределения от управляющих параметров задачи. Необходимо также определить зависимости различных составляющих массовых затрат от управляющих параметров и известных характеристик условий применения и функционирования ЭДК. С этой целью должен быть разработан комплекс математических моделей ЭДК СТТО. В работе рассматривается совокупность моделей ЭДК, разработанных для решения сформулированной выше задачи, подробно рассмотренной в работе [1].
Классификация математических моделей энергодвигательного комплекса СТТО
Комплекс математических моделей ЭДК СТТО состоит из математических моделей условий применения и функционирования ЭДК, а также математические модели энергодвига- тельных систем КА, входящих в состав СТТО (см. рисунок). Каждая модель ЭДС КА включает модели процессов функционирования, элементно-поточную матрицу ЭДС, модели массовых затрат, математические модели элементов, включая модели надежности, а также компоновочные модели, необходимые для оценки моментов инерции КА СТТО при разработке моделей ориентации и стабилизации.
Математические модели ЭДК СТТО
Математические модели условий
применения и функционирования
Математические модели
ЭДС МБ, КАО и ОКЦ
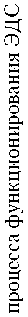



Классификация математических моделей энергодвигательного комплекса системы транспортно-технического обеспечения
Ниже рассматриваются примеры моделей условий применения ЭДК, а также процессов его функционирования. Другие типы моделей подробно рассмотрены в работах [1–4]. Модели должны отличаться сравнительной простотой, отражая основные свойства ЭДК СТТО и его элементов, поскольку применяются на ранних этапах проектирования (концептуальное и аванпроектирование).
Модели условий применения и функционирования энергодвигательного комплекса
Условия применения и функционирования задают ситуацию, в которой ЭДК СТТО выполняет свою задачу, и определяют правые части неравенств, описывающих требования к ЭДК [1, 2]. При этом их математические модели связывают величины, стоящие в правых частях неравенств, с известными характеристиками условий применения и функционирования, а в некоторых случаях и с проектными параметрами ЭДК. К известным характеристикам условий применения относятся, в частности, высота и наклонение рабочей орбиты КА ОГ (hРО и iРО), общее количество КА в группировке – NКА и т.д. К характеристикам условий функционирования относятся, например, параметры окружающей среды – плотность верхней атмосферы на высоте опорной орбиты (орбиты ОКЦ) hОКЦ, солнечная постоянная и т.п. Модель верхней атмосферы Земли может быть отнесена к числу детерминированных математических моделей условий функционирования.
Математическая модель, связывающая начальную массу КА ОГ M КА со степенью его ТО, относится к числу детерминированных математических моделей условий применения, поскольку MКА входит в правую часть неравенства, задающего требование по массе полезной нагрузки, доставляемой на рабочую орбиту МБ [1].
Однако наибольший интерес представляют стохастические модели. К их числу относится модель, описывающая связь случайной требуемой массы полезной нагрузки (ПН) КАО с известными характеристиками условий применения – параметрами КА ОГ. Данная модель необходима для определения одной из составляющих ВВЗ ЭДК – вероятности непре-вышения требуемой массы ПН КАО ее максимально допустимого значения (которое относится к числу оптимизируемых параметров). Требуемая масса ПН КАО зависит от характеристик бортовых систем КА ОГ, параметров ОГ в целом, а также стратегии и способа ТО.
В данном исследовании рассматривалась ситуация, когда КА ОГ равномерно заполняют m плоскостей рабочей орбиты, при этом в одной плоскости находится nl = NKA/m. Рассматривался вариант симметричной ОГ – все плоскости рабочей орбиты отличаются одной высотой hРО и наклонением iРО, угловые расстояния между всеми соседними плоскостями одинаковы, так же, как и угловые расстояния между соседними КА в одной плоскости рабочей орбиты. Данные допущения тем не менее не влияют на общность рассматриваемого подхода. Рассматривался вариант группового обслуживания ОГ КА: космический аппарат обслуживания в одном вылете обслуживает сразу nl КА, находящихся в одной плоскости орбиты. Было принято, что число КАО NКАО соответствует числу плоскостей рабочей орбиты, т.е. за каждым КАО закреплена своя плоскость: NКАО = m. Космические аппараты обслуживания дозаправляются и проходят регламентные обслуживания на борту ОКЦ, куда доставляются и запасные элементы КА ОГ, поэтому КАО осуществляют перелеты между орбитой ОКЦ и рабочей орбитой ОГ. Принималось, что рабочая орбита КА ОГ и орбита ОКЦ – круговые, отличающиеся друг от друга как высотой, так и наклонением.
Рассматривались две стратегии технического обслуживания: профилактическая и профилактико-восстановительная. В первом случае проводятся только периодические технические обслуживания КА ОГ: регламентная замена отказавших элементов бортовых систем вне зависимости от состояния КА между двумя техническими обслуживаниями – если произошел отказ КА, то он устраняется только в ходе ближайшего регламентного ТО. Данное обслуживание, наряду с заправкой, проводится посредством КАО с СЭРДУ. В случае профилактико-восстановительной стратегии, помимо периодических обслу-живаний, проводятся также срочные восстановительные обслуживания отказавших КА. Для этого в состав наряда КАО вводится один восстановительный КАО с двигательной установкой большой тяги (ЖРД), который постоянно находится в составе ОКЦ и осуществляет обслуживание отказавшего КА ОГ при первой же возможности – при совмещении соответствующей плоскости рабочей орбиты с плоскостью орбиты ОКЦ (при этом оперативность устранения отказа существенно выше, чем в случае профилактической стратегии).
Покажем, как находится закон распределения массы ПН КАО в случае профилактической стратегии ТО.
Принималось, что в состав полезной нагрузки КАО входят запасные элементы для систем КА ОГ, которые подразделяются на два типа: нерезервируемые (НС), надежность которых обеспечивается на внутреннем уровне, и модульного построения (резервируются целиком). К последним относятся двигатели коррекции, двигатели ориентации и аккумуляторные батареи (АБ), состоящие из элементарных аккумуляторов (ЭА). Модуль ПН КАО включает в себя детерминированную (элементы НС для nl КА и запас топлива для них) и случайную составляющие,в которые входят элементы для замены вышедших из строя ЭА, ДО и ДК на nl КА, обслуживаемых в одном вылете. Последняя составляющая носит случайный характер только тогда, когда известно количество отказавших модулей резервируемых систем. Если данная информация отсутствует, то в состав ПН КАО должен войти некоторый гарантийный запас элементов, который будет зависеть от принятого значения гарантийной вероятности, характеристик надежности элементов резервируемых систем и периода ТО. Полагаем, что система телеметрии КА выдает достаточно полную информацию о состоянии бортовых систем, поэтому причиной неопределенности в знании числа отказавших модулей АБ, ДО и ДК является конечное время перелета КАО. При формировании модуля ПН известны только те отказы, которые произошли до вылета КАО. Все последующие отказы могут быть устранены только благодаря наличию гарантийного запаса.
Таким образом, для случайной массы ПН КАО в случае профилактической стратегии технического обслуживания можно записать:
где – гарантийный запас эле ментов резервируемых систем и масса элементов АБ, ДК и ДО, отказавших на обслуживаемых в данном вылете КАО КА орбитальной группировки до его старта с опорной орбиты, здесь Т – требуемая величина, – профилактическая стратегия; – масса одной дозаправки КА из системы хранения КАО;
– масса запасных элементов для нерезерви-руемых систем одного КА ОГ.
Если время прямого перелета КАО много меньше периода ТО (Тто), то указанной выше неопределенностью можно пренебречь, т.е. считать, что в гарантийном запасе нет надобности, а параметры закона распределения величины определять за время Tто. На- против,если время прямого перелета превосходит период ТО (это возможно, если число КАО превосходит число плоскостей рабочей орбиты), то к моменту вылета КАО значение совершенно неизвестно. В этом случае общая масса запасных элементов входит в гарантийный запас,а масса модуля ПН перестает быть случайной величиной. В промежуточном случае необходимо определять величину за время , а параметры закона распределения величины находить за время . Ниже будет обо снована целесообразность регулирования тяги ЭРД КАО для обеспечения постоянства величины . Это упрощает дальнейшие рассуждения.
Сделаем несколько замечаний относительно вычисления гарантийного запаса резервных элементов. Во-первых, необходимо рассматривать разные составляющие этого запаса по отдельности, так как неизвестна не только величина , но и соотношения между количествами отказавших ЭА, ДО и ДК. Во-вторых, целесообразно не назначать значения гарантийных вероятностей,из которых находится количество запасных блоков,а оптимизировать, так как увеличение гарантийного запаса резервных элементов ведет к росту затрат на перелеты КАО. Таким обра-зом,в оптимизируемые параметры ЭДК целесообразно включить гарантийное количество резервных модулей АБ,ДК и ДО в одном модуле ПН – . Тогда
O
(Я _i_ г КА _1_ г КА
V^KAO/ ^ЛБ^^А ПДО ДО ДК ДК’ где – известные значения масс ал' ди' дк элементарного аккумулятора и единичных модулей двигателей ориентации и коррекции КА ОГ.
Найдем математическое ожидание (МО) и среднеквадратичное отклонение (СКО) требуемой массы модуля ПН КАО. Очевидно (1), что
M[ ] = n1( +) +
+ + M[], причем M[]
где , i ∈ {АБ, ДК, ДО} – математические ожидания количеств ЭА, ДК и ДО, отказавших за время .
Закон распределения времени безотказной работы резервируемых элементов КА принимается показательным [2]. Это допущение существенно упрощает дальнейшие рассуждения в рамках настоящей работы, но не влияет на общность предлагаемого подхода. В этом случае с каждой основной элементарной ячейкой АБ, а также ДК и ДО связаны простейшие потоки отказов, поскольку в случае отказа сразу же подключается резервный элемент, а вероятность того, что число отказов превысит количество резервных модулей, мала, так как должна быть мала вероятность отказа КА за период технического обслуживания T то . Сумма нескольких простейших потоков является простейшим потоком. Количества отказавших за период ТО ЭА, ДК и ДО распределены по закону Пуассона с соответствующими параметрами:
Р^ю = О = е"АБ ^: ^ =Й = ^дкАр; РС^^е-ло^,
где
_ / /\Б _ ГД О
«АБ ” 7-- ’ «ДК ” --- ’ «ДО — --- ’
Л Б ДК ДО здесь —«АБ – количество основных ЭА АБ; A™ , – требуемое число зарядно-разрядных циклов АБ за время Ас и среднее число циклов до возникновения отказа ЭА; Ак’ Ао – требуемое время работы ДК и ДО за указанный временной промежуток; Ак ’ Ао – математические ожидания продолжительности работы ДК и ДО до возникновения отказа.
Требуемое время работы ДО и ДК, требуемое количество зарядно-разрядных циклов АБ, как и характеристики надежности, относятся к исходн ой информации.
Поскольку Г = аi , i ∈ {АБ, ДК, ДО}, то значение M [ т'КАоХ' ] найдено (2). Так как количество отказавших ЭА, ДК и ДО являются независимыми случайными величинами, то среднеквадратичное отклонение для массы модуля ПН КАО:
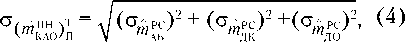
где Cmvc , i ∈ {АБ, ДК, ДО} – СКО массы отказавших модулей i-го элемента.
Тогда уравнение (4) примет вид:
С(т™Уп ~ 4^5)X^i^^
Найдем функцию распределения массы модуля ПН КАО. Данная случайная величина является дискретной, так как складывается из масс целого числа модулей ЭА, ДO и ДК. По определению функции распределения:
V(mnn) = ^kao)!! < ГА = v каоМ
= Л«0А<<Д-
где тпп = m ПН – nl ( ^нс + ^^^ 7|ПЧ ) – («АаоА .
Одно и то же значение массы отказавших элементов может быть получено множеством сочетаний различных количеств вышедших из строя ЭА, ДО и ДК. Тогда по формуле полной вероятности, учитывая независимость отказов, можно получить:
где и
Гы, ■=<„]■
иАБ идо тих тихх /
= Е Р^ = 0 Е Р(п^ = Г
? = 0^=0
min
[«/(«АБ
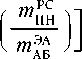
макси-
мально возможное количество запасных ЭА в
составе модуля ПН, если его масса не превосходит значение аргумента функции распределения тпн. Данная величина ограничивается либо значением аргумента, либо суммарным числом резервных ЭА на всех обслуживаемых в данном вылете КА (первый аргумент функции минимума);
/^дк у = min х maxzi
и/(идк + ^); int
mHH " ™КА
т
дк АБ
максимально возможное число ДК, входящее в состав модуля ПН при условии, что в него входит i ЭА.
(«т“)1 = т^П
о , х • Г '«ПН ” гтКА”7ткА
Д° до
"'аб
– максимально возможное количество запасных ДО в составе ПН,если число резервных ЭА равно i , а ДК – j . На основании уравнений (5) и (6), пользуясь формулой (3) и обозначив aS = a АБ + a ДК + a ДО , получим выражение для функции распределения требуемой массы модуля ПН:
А 'пн хтб^пн) = 0, т < 0;
V'(KAO/11
р/ vr(mnH) =е "'У v'^KAO/n -=q
0 < wmi < тшр
i (n;vKY ■ (n;voY. l
I x max7/ J x maxzy Л]'^ “аб у “дк ДО z ^ ^ / 1 , к ’ ’
*• j-0 J- к-0 К-
V ^ПН^ ^’ тпн
А"КАОАП
-уу1 шах • "'11Н’
где тпн – максимально возможное значение требуемой массы ПН КАО, тпи = nl [ п™ + + ^^доз +Е( г1 + 1) тк\ ], j ∈ {АБ, ДК, ДО}.
Модель процесса функционирования на примере энергодвигательной системы космического аппарата обслуживания
Процесс функционирования ЭДС КАО включает процессы создания импульса тяги, ориентации и стабилизации перед стыковками с КА орбитальной группировки и ОКЦ, обслуживания КА ОГ, генерации электроэнергии
и отвода тепловой энергии, выделяемой ин-формационно-управляющей системой (ИУС) и другими бортовыми системами КАО. Модели последних двух процессов являются детерминированными и описываются уравнениями энергомассового баланса, которые составляются на базе элементно-поточной матрицы, принцип формирования которой описан ниже. Здесь в качестве наиболее характерного и интересного примера приводится математическая модель процесса технического обслуживания ОГ КА посредством нескольких КАО.
Техническое обслуживание КА осуществляется робото-техническим комплексом (РТК), который структурно не включен в ЭДС и является по отношению к ней внешним потребителем (ВП). Потребляемая РТК электрическая мощность существенно меньше мощности, потребляемой электроракетной двигательной установкой (ЭРДУ), а значит, не определяет проектной мощности энергоустановки КАО. И потому под моделью ТО целесообразно понимать не модель процесса функционирования РТК, а модель процесса ТО всей орбитальной группировки несколькими КАО, иными словами, модель, связывающую результат данного процесса – коэффициент готовности ОГ – с временными и массовыми затратами. Достижимое значение коэффициента готовности
– случайная величина, и модель процесса ТО является стохастической.
Необходимо найти закон распределения достижимого значения коэффициента готовности. Параметры закона распределения будут зависеть от характеристик надежности систем КА ОГ, а также от периода ТО – Т то . Особенностью наряда КАО с ЭРДУ является тесная связь между T то и продолжительностью перелета. Следовательно, модель процесса ТО должна включать соотношения, связывающие период ТО с продолжительностями прямого и обратного перелета.
Рамки настоящей работы не позволяют полностью привес т и вывод закона распределения величины , а также связи периода технического обслуживания орбитальной группировки Т то с проектными параметрами ЭДК. Приведены только конечные результаты, принятые допущения и описываются основные шаги получения указанных зависимостей для случая профилактической стратегии ТО.
По определению достижимый коэффициент готовности ОГ КА г тог 1Ф где – суммарное время пребывания ОГ в неработоспособном состоянии (не функционирует штатно хотя бы один КА), а – требуемое время функционирования ОГ. На основании формулы (7) функция распределения
Кд t .
Таким образом, задача сводится к нахождению закона распределения времени неработоспособности ОГ. В общем случае величина лУ меньше, чем простая сумма периодов неработоспособности отдельных КА, поскольку при большом количестве отказов интервалы времени, в течение которых различные КА неработоспособны, могут перекрываться. Однако в практически важных случаях (когда коэффициент готовности больше 0,9) вероятность двух и более отказов КА за один период ТО весьма мала. Этот вывод полностью подтверждается результатами имитационного моделирования процесса технического обслуживания орбитальной группировки КА, которое было выполнено для верификации разработанной математической модели. Если число отказов КА мало, то мала и вероятность перекрытий. Следовательно, можно не учитывать перекрытия, полагая, что суммарное время неработоспособности ОГ равно сумме случайных периодов неработоспособности отдельных КА. В состав суммы входит случайное число слагаемых, так как количество отказов КА случайно:
где – время пребывания КА в неработоспособном состоянии, – число отказов КА за все время функционирования ОГ. Закон распределения первой величины определяется двумя факторами: законом распределения времени безотказной работы КА , от которого зависит момент наступления отказа КА, а также стратегией ТО, от которой зависит момент устранения отказа.
Как уже отмечалось, вероятность двух и более отказов одного КА за период ТО очень мала. Следовательно, суммарное количество отказов КА за время функционирования ОГ распределено по биномиальному закону: имеем NЭ = nТОNКА независимых опытов, в которых событие (отказ КА) может произойти с некоторой малой вероятностью . Здесь nТО – количество технических обслужи-ваний за время работы орбитальной группировки , а – вероятность безотказной работы КА за период ТО (предполагаем, что характеристики надежности КА после ТО восстанавливаются). Тогда вероятность появления n отказов вычисляется по формуле:
P ( = n ) = [1 – ] n [ ] .
Данное соотношение получено с учетом малой вероятности отказа КА на последнем этапе функционирования ОГ: = – n TO T то .
Биномиальные коэффициенты вычисляются по известной формуле:
r N\ .
-
3 nl(N3 - n?)
Допущение об отсутствии перекрытий интервалов неработоспособности ограничивает максимальное количество отказов КА для профилактической стратегии ТО величиной n ТО . При вычислении вероятности появления некоторого числа отказов КА это обстоятельство можно не учитывать, поскольку вероятность появления более чем n ТО отказов пренебрежимо мала. Функция распределения величины зависит от интервала времени,на котором может произойти отказ, т.е. отличается для Т то и – конечного этапа функционирования ОГ после последнего ТО (этот этап появляется, поскольку значение может быть выбрано любым, необязательно кратным T то ).
Перепишем формулу (9), учитывая, что вероятность двух и более отказов КА на конечном этапе полета пренебрежимо мала:
огк огк огк ^^ огк от к’ z = 1
где – время неработоспособности КА из-за отказа на конечном этапе полета; ,
– суммарное время неработоспособности всех КА и количество их отказов между всеми профилактическими ТО. Отказы КА мо- аУ гут отсутствовать, тогда = 0.
С учетом сказанного, пользуясь формулой полной вероятности, запишем для функции
Ау распределения :
( ) = P( < ) =+
''ОТК
+ (1 – )( ) + z отк п
Т° A
+ p( = i)( ) +
' - 1Т>тк
+ (1 – ) p( = i)( ),
^ОТК Ч)ТК где ;– вероятности отсутствия отказов КА на всех этапах функционирования ОГ между техническими обслуживаниями и конечном этапе функционирования. Третье и четвертое слагаемые правой части выражения (11) включают суммы произведений вероятностей выполнения равенств = i на значения функций распределения величины при условии на
У , А личия i отказов – ( ) и + – х ОТК' отк отк
( ). Эти функции распределения ti +tncT Ol,< отк отк получаем в предположении,что отказы имели место. Вероятность полного отсутствия отказов учитывается первым слагаемым правой части уравнения (11). Второе слагаемое учитывает наличие отказа на конечном этапе полета, когда на других этапах отказов нет. Третье слагаемое соответствует наличию отказов между ТО,но их отсутствию на конечном этапе. Четвертый член суммы отвечает наличию отказов и между ТО, и на конечном этапе полета.
Величина ( ) находится как
+ i _i_fOCT отк отк отк функция распределения суммы двух независимых случайных величин:
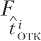
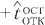
( )d ;
V ОТК' отк7
= ( ) ( – )d ,
I "£()СТХ ОТК7 ТА. \ отк отк7 отк7
О ГОТК готк
У где ( ), ( ) – функции плот- fl +/OCT /-ост
‘'ОТК отк ‘'ОТК ности распределения соответствующих случайных величин. В уравнении (12) учтены об-
ЛЕ ласти значений указанных величин: ∈ [0; ],
∈ [0; ], ∈ [0; iT ], + ∈ [0; iT + ].
то то
Очевидно, что ( ) = ( ). Функ-
^отк ^отк ция распределения времени неработоспособности ОГ при наличии двух и более отказов КА определяется как функция распределения суммы независимых величин:
тто ср „ (У ) = [ <р (tKa )ф (Г^ - fKA)dtKA;
та2 х отк7 J "Ака х отк' ука х отк отк7 отк 7
отк 0 отк отк
7 то ф,. ) = ( ф (Гка )ф , - tKA)dfKA;
ТАЗ X ОТ К7 J ТАКа \ отк/ Та 2 X ОТ К ОТ К 7 ОГК 7
отк 0 отк отк
... (13)
7то ф. ,(^) = ( ф (Гка )ф - - tKAWKA;
~£г+1х отк7 J т^ка х отк7 т£г х отк отк7 отк 7 отк 'отк 'отк
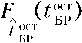
о, t-<0;
F (t°")
f KA
L БР ______________
1-PM) ’
О < гост < гк* о I БР ‘ф’
d /-ост 2> fK
( БР ^ф
Оо
Ф„ Г Ф Ока)ф - fKA)dtKA;
ТА^ X ОТК7 J т^ка х ОТК7 ТАу; —1Х 0ТК отк7 отк 7
Г 1 и о L t ' V
ОТК V отк отк
7 то
F (^) = I Ф. (t^)d^, ze[l; 77 ].
£1 х ОТК7 J '^1 х отк7 отк7 L 7
ОТК У отк
На основании уравнений (14)–(16) по-
лучаем:
Ф (ГКА) =
Y^KA отк
Соотношения (11)–(13) позволяют найти функцию распределения величины , если из вестны функции распределения величин ,
. Для профилактической стратегии ТО – это время между возникновением отказа КА и ближайшим обслуживанием, ОА е [0; Т то ].
– промежуток времени между появлением отказа КА, произошедшим позднее последнего ТО, и завершением срока эксплуатации ОГ, t1”^ е [0; ^]. Поэтому справедливы соотношения:
= Т то – ; = – , (14)
где – время безотказной работы КА, закон распределения которого находится при усло-вии,что между двумя ТО имели место отказы; – время безотказной работы КА, закон распределения которого находится при условии, что между ТО и концом эксплуатации ОГ имели место отказы. Функция распределения для профилактической стратегии ТО связана с функцией распределения времени безотказной работы КА соотношением:
0 £ка < о-
L отк ф (Т - ^КА)
^AK/Xv то ^отк7
1 БР_________________ l-T^^o)
о<е<о0;
0’С>Оо*
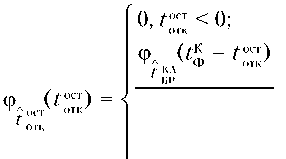
i-^X7;;,)
0<Г“"< ^;
К ф-
Совокупность выражений (8), (11)–(13), (17), (18) позволяет найти функцию распределения коэффициента готовности для профилактической стратегии ТО, если известна функция распределения времени безотказной работы КА. Она определяется характеристиками надежности бортовых систем КА:
( t ) = 1 – ( t ).
/ КЛ
ЬБР
Математическое ожидание коэффициента готовности на основании формул (7) и (10):
^2 ТО ^-КА _|_ Yjpc-'v ^cf
~ ОТК ОТК ОТК ОТК / л \
, (19)
О Ю = t то БР
0, t™<0;
0 ^вр)
КА
L БР
^ (Гто)
/ КА БР
0 V ‘ БР ■‘то’ 1 ^ТО > 7 ’ БР ТО* О (^?) + К;\ БР______________ Аналогично для величины : где , , , – математические ожидания количеств отказов и времен неработоспособности КА на этапе ТО и конечном этапе функционирования ОГ. С учетом биномиального характера распределения числа отказов и связи между МО времени безотказной работы КА и его вероятностью безотказной работы получим из уравнения (19) для профилактической стратегии ТО: Из уравнений (20)–(23) следует: D=™. Для дисперсии справедливо соотно- Ep(n r \ 0TK i= 1 шение: D = (^ +D ). Г™ t»T ---- 4 TO где otk \ (T \ x TO J БР x 7 7 При нахождении дисперсии величин и необходимо учитывать, что отказы КА могут отсутствовать. Воспользуемся связью между вторым начальным моментом случайной величины и дисперсией: , (20) £T0 f TO ' OTK ' OTK OTK где МО величины (для профилактической стратегии): гто -J P^(tW). Поскольку при полном отсутствии отказов , то справедлива формула a2..= f (1ТОУ"У p(n = 0o (tTO)dtTO = £1O J X OTK 7 ^^ r x OTK 7 '£? x OTK7 OTK OTK 0 f = 1 OTK Ято ?7TO ^^ ' V OTK 7 JV OTK 7 To X OTK7 OTK i- I 0 OTK С другой стороны, вторые начальные моменты величин выражаются через их дисперсии и МО по формулам, аналогичным формуле (20): OTK / ' 7 ,-OTK ‘otk Указанные величины вычисляются, если известны дисперсии и МО для периода неработоспособности КА после одного отказа: p ^KA otk otk ' 7 Дисперсия данной величины также может быть найдена, так как известна функция плотности распределения (17). Для нахождения необходимо воспользоваться тем же подходом, но вместо Tтоиспользовать . Приведенные выше соотношения позволяют находить функции распределения коэффициентов готовности ОГ, их математические ожидания и дисперсии для любых законов распределения времени безотказной работы КА. Зависимость достижимого коэффициента готовности ОГ от проектных параметров ЭДК СТТО проявляется через его связь с периодом технического обслуживания Тто. Приведем соотношения, отражающие данную связь. В силу наличия относительной прецессии между плоскостями рабочей и опорной орбит стартовые окна, которым соответствуют минимальные затраты характеристической скорости на перелет КАО, следуют с интервалом, равным периоду относительной прецессии . Продолжительность стартового окна мала и определяется допустимым значением дополнительного (к разности наклонений) угла не-компланарности орбит ; где ωотн – угловая скорость относительной прецессии плоскостей орбит. Оценки показывают, что при разумном значении дополнительной не-компланарности продолжительность стартового окна не может превышать 1-2 суток. Траектория движения КАО испытывает заметный прецессионный сдвиг. Угол смещения КАО (плоскости его оскулирующей орбиты) относительно плоскости орбиты ОКЦ будет зависеть от времени перелета и его схемы. Если старт КАО по выбранной плоскости рабочей орбиты состоится в момент совмещения с ней плоскости орбиты ОКЦ, то в конце перелета КАО не попадет в данную плоскость. Это связано с тем, что средняя скорость прецессии КАО выше скорости прецессии рабочей орбиты. Вылет КАО должен осуществляться с упреждением относительно момента совмеще- ния плоскостей рабочей и опорной орбит. При обратном перелете вылет также должен осуществляться до совмещения указанных плоскостей, поскольку орбита ОКЦ прецессирует быстрее переходной орбиты КАО. По этой же причине первое совмещение плоскостей опорной и рабочей орбит после вылета КАО происходит до его прибытия в плоскость рабочей орбиты. Возвращение на опорную орбиту также происходит уже после первого совмещения этих плоскостей, так как скорость их относительной прецессии всегда выше, чем скорость прецессии переходной орбиты относительно опорной. Если количество плоскостей рабочей орбиты равно числу КАО (NКАО = m), то период ТО не может быть меньше, чем 2 . Тогда для периода ТО можно записать: T = + + + + , то где , – минимальное время ожидания КАО открытия стартовых окон для прямого (на опорной орбите) и обратного (на рабочей орбите) перелетов; – продолжительность пассивной паузы. Пассивная пауза имеет место в том случае, когда период ТО выбирается больше минимально возможного. Например, оптимальное время перелета может оказаться относительно малым, если ограничения на массовые затраты не являются жесткими, поскольку это снижает время работы ЭРДУ. В то же время оптимальный период ТО,с точки зрения максимизации ВВЗ ЭДК, может оказаться больше,чем минимально достижимый при данных временах перелета. Продолжительность паузы кратна величине , как и период ТО. Время прямого и обратного перелетов КАО находится по известным формулам: время обратного перелета – детерминированная величина. Если тяга ЭРДУ не регулирует-ся,то начальное ускорение в прямом перелете будет случайным, поскольку случайна масса ПН. Тогда и продолжительность прямого перелета случайна, что может означать, во-первых, непостоянство периода ТО, а во-вторых, – серьезные трудности в планировании вылетов КАО. Действительно, стартовые окна открываются за некоторое время до совмещения плоскостей опорной и рабочей орбит – время упреждения . Если время перелета случайно, то случайным является и время упреждения. Более того, в процессе ожидания и подготовки вылета КАО это время постоянно меняется (причем скачкообразно), поскольку из-за случайных отказов на борту КА ОГ изменяется масса модуля ПН. Возможна ситуация, когда из-за очередного внезапного отказа на КА ОГ штатный вылет КАО вообще становится невозможным: вылет приходится отложить до следующего стартового окна. Во избежание указанных трудностей необходимо зафиксировать начальное ускорение КАО, а тягу ЭРДУ регулировать в зависимости от массы ПН. Начальное ускорение обратного перелета вычисляется для максимальной тяги ЭРДУ , поскольку целесообразно сокращать время ее работы: /^КАОХ ^ЭРДУ х1Л0 /ОН = ----------- МКАО + Ог*<А0)гт сух х Т /ОП тпКА0 VP КУ* ЭРДУ п као 1- ехр уп Л X ^КАО ЭРДУ у где – затраты топлива на обратный перелет; – «сухая» масса КАО. Для определения времен ожидания стартовых окон необходимо найти значения прецессионных сдвигов плоскостей переходных орбит КАО за время прямого и обратного перелетов. Угловая скорость прецессии орбиты радиуса r с наклонением iорбвычисляется по известной формуле [5]: Ц/КАО ЭРДУ V^o /ОП 1- ехр к0 ЦЛКАО ЭРДУ J где , – затраты характеристической скорости на обратный и прямой перелеты КАО; , – начальные ускорения КАО в прямом и обратном перелетах; – удельный импульс ЭРДУ КАО. Поскольку в обратном перелете КАО не транспортирует ПН, а его собственная сухая масса – величина неизменная, начальное ускорение фиксировано. Таким образом, где e3– третий коэффициент в разложении гравитационного потенциала Земли в ряд по сферическим функциям; µ3– гравитационный параметр Земли. Тогда угловая скорость относительной прецессии опорной и рабочей орбит: ,,7/2 ОО COSZoo COSZpo ,-7/2 ' РО / где rOO, rPO, iOO, iPO– радиусы и наклонения опорной и рабочей орбит. Период относительной прецессии: уотн пр 2л В соотношениях (29) учтено, что интерес представляют только части этих углов, получаемые путем отбрасывания целого числа полных «оборотов» КАО относительно рассматриваемых плоскостей. Времена упреждения (от момента вылета Траектория полета КАО с СЭРДУ близка к круговой спирали. В пределах одного витка радиус и наклонение можно принять постоянными. Тогда может быть введено понятие мгновенной угловой скорости прецессии оскулирующей орбиты КАО ΩКАО(t), которая вычисляется по формуле, аналогичной формуле (27). Полные углы сдвига плоскости орбиты КАО за время прямого и обратного перелетов: см пп COS/ ХО . оро dp г(07/2 КАО до рабочей мулам: ближайшего совмещения плоскостей и опорной орбит) находятся по фор- шупр тПП Von /упр = -----. /упр = —: ПП Q ’ On Q . Зная продолжительность перелетов и упреждения,можно отыскать время запаздывания моментов прибытия КАО на рабочую и опорную орбиты по отношению к последнему моменту совмещения плоскостей этих орбит: ^КАО _ ^-упр -зап — ^КА^ _ £УПР _ Тотн jp4- пер IIII КАО пер ПП 1 пр ------------- Тотн X пр / -КАО ез г COSTCO dr » г<о7/2 /Узап \ = -КАО _ а-упр _ -роти • А КАО/ОО lO ‘оп 2 пр L Зависимости наклонения и радиуса орбиты от времени iорб(t) и r(t) были найдены через текущие значения затрат характеристической скорости с использованием соотношений, приведенных в работах [6, 7] для задач оптимизации перелетов с малой тягой между круговыми некомпланарными орбитами. Углы прецессионного сдвига КАО относительно обслуживаемой плоскости рабочей орбиты в прямом перелете и относительно опорной орбиты в обратном перелете были названы углами упреждения и , поскольку именно такие углы должны иметь место (при отсчете от плоскости опорной орбиты в направлении ее прецессии) между плоскостями опорной и рабочей орбит перед вылетами КАО: Тогда времена ожидания КАО открытия стартовых окон: ТРО 1ож ТОО 1ОЖ шУпР = О тКАО — ш^М — УрП OOLO тОП - 2лint ш* т пп = шсм - П тКЛ0 ^ПП РО пер - 2л int - Q тКЛ0 РО пер 2л где ΩΟΟ, ΩРΟ– скорости угловой прецессии опорной и рабочей орбит. Т’отп ^зап /-упр пр ^КАО Ч)П> при Гш“ - too - toil > С + fCT + С;- ОТ^отн ^-зап /-vnp tip Ч<АО miP при J^OTH пр при Тотн_ v-зап _ ^vnp / ^КА _i_ v-KA _l ^КА 1 ПР ^КАО ^С)П 6Ф LCT обсл’ _ /^зап \ _ ^упр Х^КАО/ОО ^ПП’ Т'отп _ /^-зап \ _ у-упр > у-ОКЦ _|_ ^ОКЦ. ПР Х^КАО^ОО ПП СТ обсл ’ ОТотн /у-зап \ _ /-упр пр Х^КЛО/ОО 1111’ ппи Т°™ — (t™1 1 — Лу"₽ < Т01<Ц + /ОКЦ ( )ОО где – суммарная продолжительность стыковок КАО со всеми КА ОГ, находящимися в одной плоскости рабочей орбиты, суммарное время их обслуживания, а также продолжительности процесса стыковки КАО с ОКЦ и обслуживания на нем соответственно; – суммарное время фазирований орбиты КАО для обслуживания всех КА ОГ, находящихся в одной плоскости рабочей орбиты. Совокупность соотношений (24)–(26), (28)–(31) позволяет определить минимально возможный при заданном значении начального ускорения КАО аоА° период ТО и множество возможных значений периода ТО: Train = -KAO , С>О_1_ ТКАО + -РО. И) пер ож О о ж 7 у = J’min _^_ ^КАО. ^КАО — Q. J'oth . ^У0™- ^у»та. ТО ТО пауз7 пауз 7 пр 7 пр 7 пр 7‘“ Выводы Результатом данной работы является комплекс математических моделей, использование которых позволяет формализовать задачу параметрического синтеза ЭДК СТТО – получить функциональные зависимости вероятности выполнения задачи ЭДК (целевой функции) и суммарных массовых затрат (ограничение задачи) от его проектных параметров. Предложенные математические модели достаточно универсальны и могут использоваться при оптимизации ЭДК СТТО различной структуры [1, 2, 8, 9], включая сравнительно простые, без орбитального космического центра и многоразовых средств развертывания. Подобные СТТО могут быть созданы в обозримом будущем.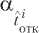
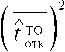
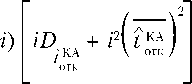
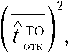
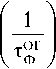
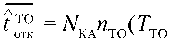
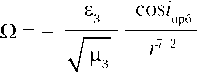
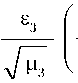
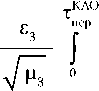
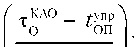
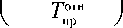

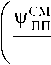
Список литературы Математические модели энергодвигательного комплекса системы транспортно-технического обеспечения для развертывания и обслуживания орбитальной группировки космических аппаратов
- Евдокимов Р.А., Чилин Ю.Н. Параметрический синтез энергодвигательного комплекса системы транспортно-технического обеспечения орбитальной группировки КА//Космические исследования. 2013. № 3. Т. 5. С. 250 -264.
- Чилин Ю.Н. Основы комплексной оптимизации космических энергодвигательных систем. СПб.: ВИККА им. А. Ф. Можайского, 1998. 255 с.
- Чилин Ю.Н., Евдокимов Р.А. Комплексное обоснование структуры и параметров энергодвигательной системы КА//Космические исследования. 2001. Т.39 (вып.5). С. 537-549.
- Тимашев С.В., Кузьмин А.А., Чилин Ю.Н. Оптимизация энергетических систем орбитальных пилотируемых станций. М.: Машиностроение, 1986. 232 с.
- Полет космических аппаратов: Примеры и задачи: Справочник/Авдеев Ю.Ф., Беляков А.И., Брыков А.В. и др.; Под общ. ред. Титова Г.С. 2-е изд., перераб. и доп. М.: Машиностроение, 1990. 272 с.
- Сафранович В.Ф., Эмдин Л.М. Маршевые двигатели космических аппаратов. Выбор типа и параметров. М.: Машиностроение, 1978. 240 с.
- Салмин В.В. Оптимизация космических перелетов с малой тягой. М.: Машиностроение, 1987. 208 с.
- Грибков А.С., Лопота В.А., Легостаев В.П. и др. Электроракетный транспортный аппарат для обеспечения больших грузопотоков в космосе//Известия РАН. Энергетика. 2009. № 2. С. 101-111.
- Легостаев В.П., Лопота В.А., Синявский В.В. Перспективы и эффективность применения космических ядерно-энергетических установок и ядерных электроракетных двигательных установок//Космическая техника и технологии. 2013. № 1. С.4-16.


