Математические модели киральных метаматериалов на основе многозаходных проводящих элементов

В настоящее время в электродинамике и оптике активно исследуются метаматериалы, то есть искусственно создаваемые структуры, обладающие нетрадиционными для естественных сред свойствами взаимодействия с электромагнитным полем [1; 2]. Метаматериалы имеют в своей основе искусственную периодическую структуру, за счет которой изменяются материальные параметры метаматериала в целом, что, в свою очередь, приводит к изменению дисперсионных, поляризационных характеристик и т. п. Любой метаматериал состоит из однородного контейнера, в котором периодически размещаются элементы, размеры которых соотносятся с длинами волн падающего электромагнитного излучения.

С другой стороны, начиная с конца ХХ века в электродинамике СВЧ значительно возрос интерес к исследованию и созданию композитных и искусственных сред, обладающих свойством ки-ральности [3–7]. Киральная среда (метаматериал) представляет собой совокупность равномерно распределенных в изотропной диэлектрической среде проводящих зеркально-асимметричных

(киральных) элементов. Помимо материала, из которого изготовлен киральный элемент, важнейшую роль играет и его форма. Именно поэтому так важно исследование новых видов киральных элементов, а также определение электродинамических свойств киральных метаматериалов на их основе.

Основными свойствами киральных метаматериалов являются распространение волн с право-и левокруговыми поляризациями, а также кроссполяризация падающего электромагнитного излучения, возникающая при прохождении и отражении от кирального метаматериала. В общем случае во всех окружающих киральный метаматериал областях электромагнитные волны будут иметь эллиптическую поляризацию.

Одной из наиболее известных киральных частиц является элемент Телледжена [8], представляющей собой совокупность разомкнутого тонкопроволочного кольца и выступающих прямолинейных концов. Любой киральный элемент представляет собой совокупность электрического и магнитного диполя, что, в свою очередь, приводит к возникновению дополнительной связи меж

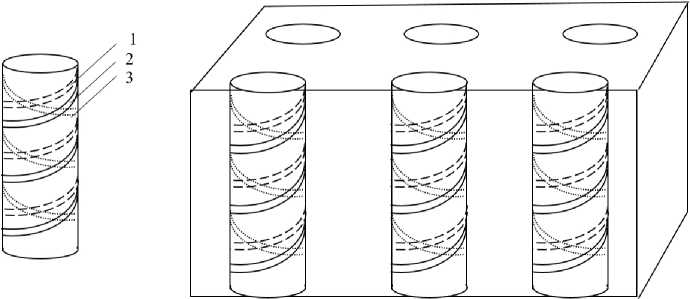
Рис. 1. Геометрия элемента и метаматериала

Fig. 1. The geometry of the element and metamaterial

ду электрическими и магнитными индукциями и напряженностями, которая в материальных уравнениях описывается так называемым параметром киральности.

Данная работа посвящена построению математических моделей и исследованию отражения электромагнитных волн СВЧ-диапазона от метаматериалов, созданных на основе составных элементов с произвольным числом заходов - много-заходных спиралей и гаммадионов. В научной литературе подробно исследованы электромагнитные свойства классического (двухзаходного) гаммадиона [9]. Также изучены частотно и поляризационно-селективные свойства метаматериала на основе элементов Телледжена и однозаходных тонкопроволочных спиральных элементов [10]. Доказано, что подобные структуры могут выполнять роль частотно-селективных преобразователей падающего электромагнитного излучения заданной частоты в рассеяние в азимутальной плоскости. В работе [11] рассмотрено решение задачи об отражении плоской электромагнитной волны СВЧ от метаматериала, состоящего из совокупности составных элементов, представляющих собой две ортогональные трехмерные тонкопроволочные спирали. Доказано, что эффекты киральности в таком метаматериале возникают только в случае, когда спирали в составе элемента не являются тождественными по геометрическим и электрофизическим параметрам.

В предлагаемой работе построены математические модели с учетом дисперсии метаматериалов на основе составных элементов двух типов: N-ортогональных спиралей и N-заходных гамма-дионов, а также проведен анализ отражения плоской электромагнитной волны линейной поляризации от планарных слоев двух указанных типов метаматериала. Для структурного описания метаматериалов будет использоваться модель Максвелла Гарнетта [7].

1. Математическая модель метаматериала на основе составных спиральных элементов

Рассмотрим построение математической модели составного элемента на основе произвольного числа спиральных элементов, а также метаматериала на основе периодически распределенной матрицы таких элементов. Геометрия элемента и метаматериала показаны на рис. 1. Для простоты на рис. 1 показаны 3 спирали (1-3) в структуре составного элемента.

Спирали внутри составного элемента отличаются друг от друга своими геометрическими параметрами. Однако при создании метаматериала на их основе все составные элементы должны быть тождественными. Обозначим геометрические параметры i -й спирали в киральном элементе через N_i – число витков; R_i – радиус витка спирали; h_i – шаг спирали; l_i – длину спирали в расправленном состоянии; r - радиус проволоки; a i - угол накрутки спирали.

Для расчета резонансной частоты составного элемента воспользуемся формулой Томсона:

® 0 =

^, LC

где L - общая индуктивность составного элемента; C – общая емкость составного элемента.

Индуктивность и емкость составного элемента определяются следующим образом:

N        N    ( N  ) ¹

C = Е C . ; L = п 4L L i = 1            i = 1     V i = 1 J

где L_i – индукт ивн ость i -й спирали; C_i – емкость i -й спирали ( i = 1, N ); N - общее число спиралей в составном элементе.

Емкость одной спирали определяется следующим образом [11]:

C i = C пр i + c mb i + C M3 i , (3) то есть в виде суперпозиции емкостей тонкопроволочного проводника, межвитковой емкости i -й спирали и межэлементной емкости.

В результате выражение для общей емкости i -й

спирали имеет вид:

C i = ⁸ c2

------¹ 10 ^{- 11} +

18ln | ^ |- 1

I r i J

материала; c – скорость электромагнитной волны в вакууме; A – параметр, имеющий размерность длины и связанный с расстоянием между элементами; в о - параметр, имеющий размерность частоты и связанный с внутренними процессами в среде.

Из первого соотношения (7) получается формула для относительной эффективной диэлектрической проницаемости метаматериала:

”[ ( R i + ² r i ) 2 - R i ² ] ( N i - 1 )

₊ 1 N i ⁽ R i ⁺ r i ) r d cos a i   i

1 + 208 x2, _р _ ⁸ c2 ^{- 8} s2

• ⁸ 2 = ⁸ s2             ^{; 8} x2 =       _?     .

• ^{1    - a8} x2            ⁸ c2 ^{+ 2 e} s2

В результате выражения для эффективной диэлектрической проницаемости и параметра ки-ральности метаматериала на основе составных спиральных элементов имеют следующий вид:

где s c2 - относительная диэлектрическая проницаемость контейнера (цилиндрической основы, на которую намотана спираль).

Индуктивность i-й спирали определяется следу ющим соотношением:

^е 2

1 + 2 08 2

= е« 2-------- ;

^{1 - a8} x2

_Р _ ⁸c2   ⁸ s2 .

⁸ x2 "f + 2f ; ⁸ c2 ^{+ 2 8} s2

⁸ s2 ( ^to ) = ⁸ c2 ■ ₂⁰₂ to o -to

X 2 ( ^to ) =

A P 2 to c ( to 2 - to ²

Как известно, в киральных метаматериалах

, _    п Ni² Ri²

Li = ^c2     ,     , li

имеет место распространение двух волн с право-и левокруговыми поляризациями, волновые числа которых определяются следующим образом:

где ц _с2 - относительная магнитная проницаемость контейнера.

Формула для резонансной частоты составного

^ R.L "  c (V ⁸ 2 ^ 2 ±^x 2 ) .

спирального элемента

получается из соотноше-

ний (1), (2), (4) и (5):

Подставляя в формулы (10) выражения (9), получаем соотношения для вычисления волновых чи-

^to 0 =

N ( N ) 1 N П L IL.  I С i=1    (i=1 J i=1

- 1/2

где C_i и L_i определяются соотношениями (4) и (5).

После вычисления резонансной частоты составного спирального элемента воспользуемся формулой Максвелла Гарнетта с учетом дисперсии [12]:

⁸ 2 ^-8 s2 =_a ⁸ c2 ^-8 s2 _;

⁸ 2 ⁺ 2 ⁸ s2      S c2 + 2 S s2’

⁸ s2 ^(to) = ⁸ c2

p0    .

;

to o -to

X 2 ( ^to ) =

A ^ O to

22 c I to o - to

где S 2 - относительная эффективная диэлектри

ческая проницаемость метаматериала; s s2 - относительная диэлектрическая проницаемость кирального элемента на цилиндрической основе; a - объемная концентрация составных спиралей; Х 2 - относительный параметр киральности мета-

сел волн с право- и левокруговыми поляризациями в киральном метаматериале:

^ R.L "  k 0

I ^{1 + 2 a8} x2 ₊ ⁸c9 “         ±

^{1 - a8} x2

^c ( to

) A P 2 to

■ 0-

to 2 )_j ,

в которой резонансная частота to 0 определяется формулой (6); к 0 = to/ c - волновое число для плоской электромагнитной волны в вакууме.

2. Математическая модель метаматериала на основе N-заходных гаммадионов

Рассмотрим построение математической модели составного элемента на основе N-заходных гаммадионов, а также метаматериала на основе периодически распределенной матрицы таких элементов. Геометрия элемента и метаматериала показаны на рис. 2. Для простоты на рисунке изображены: 4-заходный гаммадион и метаматериал на основе двухзаходных гаммадионов.

Заходы (S-элементы) в структуре N-заходного гаммадиона отличаются друг от друга своими гео-

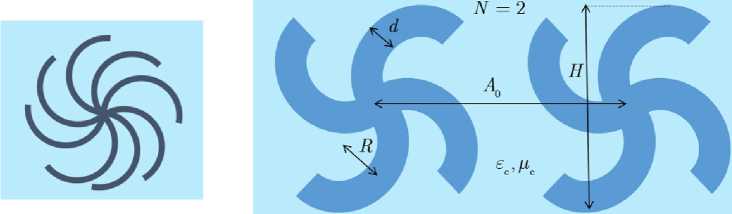
Рис. 2. Геометрия элемента и метаматериала

Fig. 2. The geometry of the element and metamaterial

метрическими параметрами. Однако при создании метаматериала на их основе все гаммадионы должны быть тождественными. Обозначим геометрические параметры i -го S-элемента в структуре гаммадиона через R_i – радиус; d_i – ширина металлической полоски; H_i – высота S-элемента.

Для расчета резонансной частоты составного элемента воспользуемся формулой Томсона (1), в которой теперь L – общая индуктивность N-заходного гаммадиона; C – общая емкость N-заходного гаммадиона.

Индуктивность и емкость N-заходного гамма-диона определяются следующим образом:

N         N    ( N  ) ¹

C = X С . ; L = П L i X L i i = 1              i = 1     ( i = 1    )

где L . - индуктивность i -го S-элемента; C . - емкость i -го S-элемента ( i = 1, N ); N - общее число S-элементов в гаммадионе.

Емкость гаммадиона вычисляется как

C = C + C M3 ,

Индуктивность N-заходного гаммадиона опре- деляется следующим соотношением:

2 2 NR ²

L = ^ c2

Формула для резонансной частоты N-заходного гаммадиона получается из соотношений (1), (16) и (17):

го =     1            ² A о h

⁰ V ^s c2 ^ c2 NR у/ п H ( 4 A о + h ) .

После вычисления резонансной частоты составного спирального элемента воспользуемся формулой Максвелла Гарнетта с учетом дисперсии (7), в которой Б2 - относительная эффективная ди- электрическая проницаемость метаматериала на основе N-заходных гаммадионов; Бs2 - относительная диэлектрическая проницаемость области, занятой гаммадионами; а - объемная концентра- ция гаммадионов.

В результате выражения для эффективной диэлектрической проницаемости и параметра ки-ральности метаматериала на основе N-заходных гаммадионов имеют следующий вид:

то есть в виде суперпозиции емкостей самого гам-мадиона и межэлементной емкости.

Собственная емкость гаммадиона рассчитыва ется как

^Б 2

= ^Б s2

^{1 + 2 аБ} х2 .

^{1 -аБ} х2 ’

_Б = ^Б с2 ^-Б s2 . x ²   Б с2 + 2V

2 п NRd

C 3 == c2 ”

^Б s 2 ( ^го ) = ^Б c 2

в 2

2    2

X 2 ( ^го ) =

А в о го c ( го о - го ²

где h – толщина контейнера метаматериала.

Межэлементная емкость определяется по формуле:

C ìý

= ^Б с2

п NRd

² A о ,

где А о - расстояние между центрами соседних гаммадионов.

В результате выражение для общей емкости N-заходного гаммадиона имеет вид:

С = 2 п N s c2 Rd

4 А о + h

4 A ₀ h

Волновые числа собственных волн метаматериала определяются формулой (10). Подставляя в соотношения (10) выражения (19), получаем соотношения для вычисления волновых чисел волн

с право- и левокруговыми поляризациями в ки-ральном метаматериале на основе N-заходных гаммадионов:

k R.L

= k о

Г ,----------------------

1 + 2 ^а Б х2

, Бс9

s ^{2 1} -аБ х2

) А Р 2 го c ( го 2 - го ² )

Подставляя в формулу (20) выражение для резонансной частоты N-заходного гаммадиона (18),

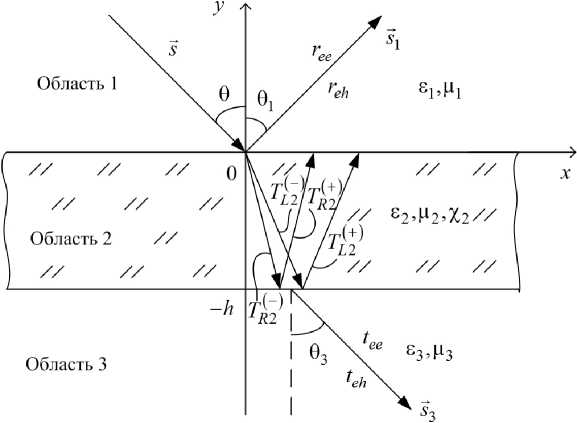
Рис. 3. Геометрия задачи

Fig. 3. The geometry of the problem получаем итоговые соотношения для волновых чисел волн с право- и левокруговыми поляризациями в метаматериале.

• 3 . Задача об отражении волны от планарного слоя метаматериала

В качестве примера рассмотрим решение задачи о падении плоской электромагнитной волны E-поляризации на планарный слой кирального метаматериала (на основе составных спиральных элементов или N-заходных гаммадионов), который является бесконечно протяженным вдоль оси Oz . Геометрия задачи приведена на рис. 3. На метаструктуру из диэлектрической области 1 ( е 1 и ц 1 - относительные диэлектрическая и магнитная проницаемости) под произвольным углом 9 падает плоская электромагнитная волна линейной перпендикулярной поляризации.

Область 2 представляет собой слой кирального метаматериала толщины h ( б ₂ и Ц 2 - относительные диэлектрическая и магнитная проницаемости; % 2 - относительный параметр киральности). Область 3 представляет собой диэлектрик ( б ₃ и ц ₃ - относительные диэлектрическая и магнитная проницаемости).

Целью является получение выражений для коэффициентов отражения основной ( r _ee ) и кросс-поляризованной ( r _eh ) компонент поля в области 1, а также формул для коэффициентов прохождения основной ( t ee ) и кросс-поляризованной ( t eh ) компонент поля в области 3.

Киральная среда описывается следующими материальными уравнениями [3–6]:

D ⁽²⁾ =б ₂ ( и ) Е '2' + i х ₂ ( и ) Н®, B '2I=^2 Н® ± i х ₂ ( и ) Е ^|2\

где верхние и нижние знаки определяют правую или левую форму киральных элементов. Соотношения (1) записаны в Гауссовой системе единиц.

Векторы напряженностей электрического и магнитного полей в слое из кирального метаматериала находятся из следующих дифференциальных уравнений [5]:

• V ² Е ⁽²⁾ + к 0 ( б ₂ ц ₂ +х 2 ) Е ⁽²⁾ - 2 ik 2 Ц ₂ Х ₂ Н ⁽²⁾ = 0;

• V ² Н ⁽²⁾ + к 0 ( б ₂ ц ₂ + х 2 ) Н ⁽²⁾ + 2 ik ² б ₂ / ₂ Е ⁽²⁾ = 0.

Векторы напряженностей электрического и магнитного полей в слое из кирального метаматериала представляются в виде суперпозиции полей волн с круговыми поляризациями [3]

Е® = Е r + ЕL Н® - i Е ( Е r - Е l ) ,          (23)

^ 2

в результате чего получаются однородные уравнения Гельмгольца для циркулярнополяризованных волн:

• ^V 2 ^ЕR , L ± ^kR , 1^ЕR , L = ⁰ , ( ² 4) где Е r - напряженность электрического поля волны c правой круговой поляризацией; Е l - напряженность электрического поля волны с левой круговой поляризацией.

Решения уравнений (24) представляют собой совокупность двух волн, прошедших в киральный метаматериал, и двух волн, отраженных обратно в слой метаматериала от границы раздела с областью 3 [5; 11]:

E ( 2 ) = t ^{( - )} e ik R ⁽ —— r , — ) ₊ t ^{( +} ) e i ^kR ⁽ —— r , — ) ₊

новной компоненты; t _eh – коэффициент про-

+ T ( ^{- )} e ik L ⁽ * L , — ) + T ( + ) e ik L ⁽ S L , Г )_;

хождения кросс-поляризованной компоненты; n ^{( 3} ) = J ^ 3/^е3 - импеданс области 3; k 3 = k 0^ Б 3 Ц 3 -

H(2)

i

П 2

_T ^- e ^{- ik}R ^{( S} R , ^S ) _{+ T} + ) e ik R ^{( S} R , ^S ) _

- T ^{( -} e - ik L ^{( —} L , ^— ) - T ^{( +} ) e ik L ^{( ?} L , * )

волновое число для плоской однородной волны в

области 3.

гДе ^S R , L = {

sin ⁶ R , L , ^- cos ⁶ R , L }

– орты, вдоль кото-

рых распространяются прошедшие в метамате-

риал волны; — R⁺L = { sin 6 rl ,cos 6 rl } — орты, вдоль которых распространяются отраженные от обла-

На границах раздела выполняются следующие граничные условия для тангенциальных составляющих векторов напряженностей электрического и магнитного полей:

сти 3 волны; 6 r l — углы преломления волн с круговыми поляризациями; n ⁽ 2 ) = ^Ц 2 /^е 2 — импеданс кирального слоя; t R ~^ и tL ¹ - коэффициенты

–

прохождения волн с круговыми поляризациями;

t R ⁺ ) и t L ⁺ ) - коэффициенты отражения волн с круговыми поляризациями в слой метаматериала.

E T ¹ ) ( y = 0 ) = E® ( y = 0 ) ;

H T ¹ ) ( y = 0 ) = H T ¹ ) ( y = 0 ) ;

E < ²⁾ ( y = - h ) = E T ³⁾ ( y = - h ) ; ih T ²⁾ ( y =- h ) = h T ³⁾ ( y =- h ) .

Составляющие векторов напряженностей электрического и магнитного полей в области 1 в слу-

чае падения плоской электромагнитной волны E-поляризации имеют следующий вид:

После подстановки соотношений (25), (26) и (27) в граничные условия (28) получаем неоднородную систему линейных алгебраических уравнений следующего вида:

E_z (1)

- ik ( s,г )         - ik ( — , г )

= e ¹       + те ^{1 т} ;

ee              ;

^^ —*     —*

AT = P ,                                        (29)

где J A - матрица 8 x 8, явный вид элементов которой не приводится в силу их значительного объема;

COS 6 - ik ( s , г ) COS 6 - ik ( — , r )

11 r

H x ( 1 ) e          ⁺ r ee ( 1 ) e ^;

n              n

(1)__r -i ik 1 ⁽ * т , ^S ).

H z = ' eh ^e         ;

^T = [ r ee r eh ^TR ^{+ T}R "’ ^TL ⁺ ) ^TL ") t ee t eh ] ; P = [ 0 - 1 cos 6 ₁ /n⁽¹⁾ 00000 ] .

c(l)           (1)         - ik ( — , ^S )

E X ) =- r eh n cos 6 e ^{1 T} ,

где s_T = { sin 6 ,cos 6 } - орт, показывающий направление распространения отраженной волны в об-

Из решения системы линейных алгебраических уравнений (29) определяются неизвестные коэффициенты отражения и прохождения основных и кросс-поляризованных компонент поля.

ласти 1; r _ee – коэффициент отражения основной

компоненты; reh – коэффициент отражения кросс- поляризованной компоненты; ki = k0^б^ - вол-

новое число для плос кой однородной волны в

области 1; n ⁽ )^: ской области 1.

Б 1 - импеданс диэлектриче-

Составляющие векторов напряженностей электрического и магнитного полей в области 3 в случае падения плоской электромагнитной волны E-поляризации имеют следующий вид:

E

. (з)

z

= t==e ee

^ik 3 ( ^S 3 , ^S ).

;

H

(3)

z

= t eh ^e

^ik 3 ( ^S 3 , ^S ).

;

E

• (3)

x

= t eh n

, (3)

cos 6 3 e

^ik 3 ( ^S 3 , ^S ).

;

(3)

x

-

t ee

COs 6 ₃

n

.(3)

e

^ik 3 ( ^S 3 , ^S ) .

;

где S 3 = { sin 6 3 , - cos 6 3 } - орт, показывающий направление распространения прошедшей волны в области 3; t _ee – коэффициент прохождения ос-

• 4.    Численные результаты

  • 4.1.    Метаматериал на основе составных спиральных элементов

В качестве примера была рассмотрена структура на основе составного элемента, состоящего из 3 тонкопроволочных спиралей. Толщина слоя метаматериала – 0,05 м. Материал контейнера имеет относительную диэлектрическую проницаемость б _с 2 = 1,5. Параметры двух тонкопроволочных спиралей в составном элементе были идентичными: R ₁₂ = 0,01 м, N 12 = 3, т ₁₂ = 0,002 м, H 12 = 0,05 м, ^ 12 = 0,05 м; третья спираль отличалась от первых двух числом витков: R 3 = 0,01 м, N 3 = 2, т 3 = = 0,002 м, H 3 = 0,05 м, d 3 = 0,05 м. Области 1 и 3 представляли собой вакуум с Б 13 =^ 13 = 1. Падение волны на метаструктуру происходило по нормали: 6 = 0.

На рис. 4 представлены частотные зависимости модулей коэффициентов отражения основной ( r _ee – сплошная линия) и кросс-поляризованной

компонент ( r eh - штриховая линия), а также коэффициентов прохождения основной (| t ee| - сплошная линия) и кросс-поляризованной компонент (| t eh | - штрихпунктирная линия) для метаматериала на основе составных элементов из 3 спиралей.

Как видно из рис. 4, уровень прохождения основной компоненты поля уменьшается с ростом частоты; уровни отражения и прохождения кросс-поляризованной компонент практически не изменяются во всем частотном интервале исследования. На частотах 3,8 и 6,9 ГГц имеются резкие минимумы модуля коэффициента прохождения основной компоненты.

На рис. 5 представлены частотные зависимости отраженной мощности основной (10lg r _ee ² – сплошная линия) и кросс-поляризованной компонент (10lg r _eh ² – штриховая линия), а также прошедшей мощности основной (10lg _ee – сплошная линия) и кросс-поляризованной компонент (10lg t _eh ² – штрихпунктирная линия) для метаматериала на основе составных элементов из 3 спиралей.

Как видно из рис. 5, на частоте 6,9 ГГц структура не пропускает основную (падающую) компонен- ту электромагнитного поля при низких уровнях отражения основной компоненты, а также отражения и прохождения кросс-поляризованной компоненты. Такая ситуация соответствуют преобразованию нормально падающего СВЧ-излучения в азимутальное рассеяние. Также можно заметить, что практически на всем частотном интервале исследования уровни отражения основной и прохождения кросс-поляризованной компоненты практически одинаковые, что связано с ярко выраженными поляризационно-селективными свойствами кирального метаматериала. На частоте 4,2 ГГц имеет место небольшой локальный максимум отражения кросс-поляризованной компоненты поля, а также ее прохождения.

Таким образом, как и для случая составного элемента из двух взаимоортогональных спиралей [11], доказано, что существуют дискретные частоты, на которых происходит преобразование нормально падающего СВЧ-излучения линейной поляризации в азимутальное рассеяние. Как показали дополнительные исследования, для того, чтобы возникли подобные эффекты необходимо, чтобы либо число спиралей в составном элементе было нечетным, либо при четном числе спиралей необходимо, чтобы они отличались друг от друга геометрическими параметрами.

• 4.2. Метаматериал на основе N-заходных гам-мадионов

В этом случае была рассмотрена структура на основе трехзаходного гаммадиона. Толщина слоя метаматериала – 0,05 м. Материал контейнера имеет относительную диэлектрическую проницаемость s c2 = 1,5. Параметры гаммадиона: R = 0,01 м, N = = 3, d = 0,02 м, H = 0,05 м. Области 1 и 3 представляли собой вакуум с s ₁₃ = ц ₁₃ = 1. Падение волны на метаструктуру происходило по нормали: 9 = 0.

На рис. 6 представлены частотные зависимости модулей коэффициентов отражения основной ( ree – сплошная линия) и кросс-поляризованной компонент ( reh – штриховая линия), а также коэффициентов прохождения основной ( tee – сплошная линия) и кросс-поляризованной компонент ( teh – штрихпунктирная линия) для метаматериала на основе совокупности 3-заход- ных гаммадионов.

Как видно из рис. 6, уровень прохождения основной компоненты поля уменьшается с ростом частоты; уровни отражения и прохождения кросс-поляризованной компонент практически не изменяются во всем частотном интервале исследования, аналогично как и для случая составного спирального элемента. На частотах 3,4 и 3,9 ГГц имеются резкие минимумы модуля коэффициента прохождения основной компоненты, по величине более «глубокие», чем в случае метаматериала на основе составных спиральных элементов.

На рис. 7 представлены частотные зависимости отраженной мощности основной (10lg r _ee ² – сплошная линия) и кросс-поляризованной компонент (10lg r _eh ² – штриховая линия), а также прошедшей мощности основной (10lg t _ee ² – сплошная линия) и кросс-поляризованной компонент (10lg t _eh ² – штрихпунктирная линия) для метаматериала на основе совокупности 3-заход-ных гаммадионов.

Как видно из рис. 7, на частоте 3,4 ГГц структура не пропускает основную (падающую) компоненту электромагнитного поля при низких уровнях отражения и прохождения кросс-поляризованной компоненты. Однако степень преобразования мощности падающей СВЧ-волны в азимутальное рассеяние меньше, чем для случая метаматериала на основе составных спиральных элементов, так как на этой частоте возрастает уровень отражения основной компоненты поля.

Такая ситуация соответствуют преобразованию нормально падающего СВЧ-излучения в азимутальное рассеяние. Также можно заметить, что

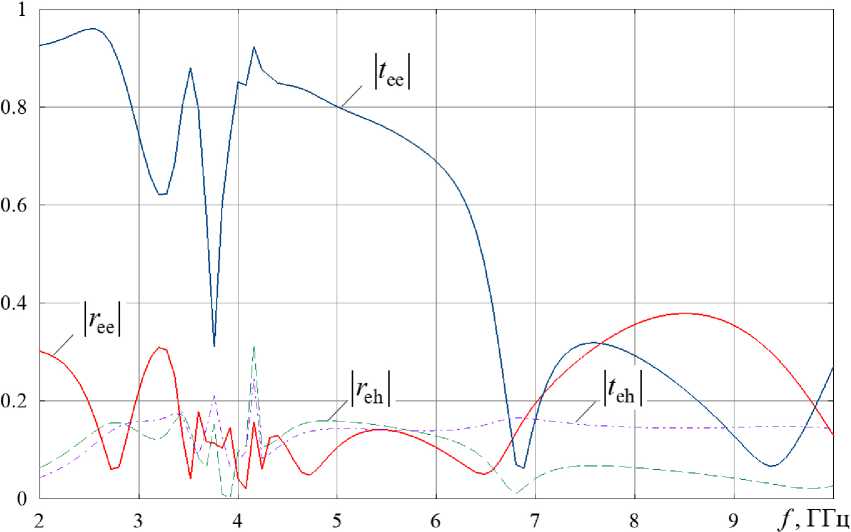
Рис. 4. Частотные зависимости модулей коэффициентов отражения и прохождения для метаматериала на основе составных элементов из 3 спиралей

Fig. 4. Frequency dependences of the moduli of reflection and transmission coefficients for a metamaterial based on constituent elements of 3 spirals

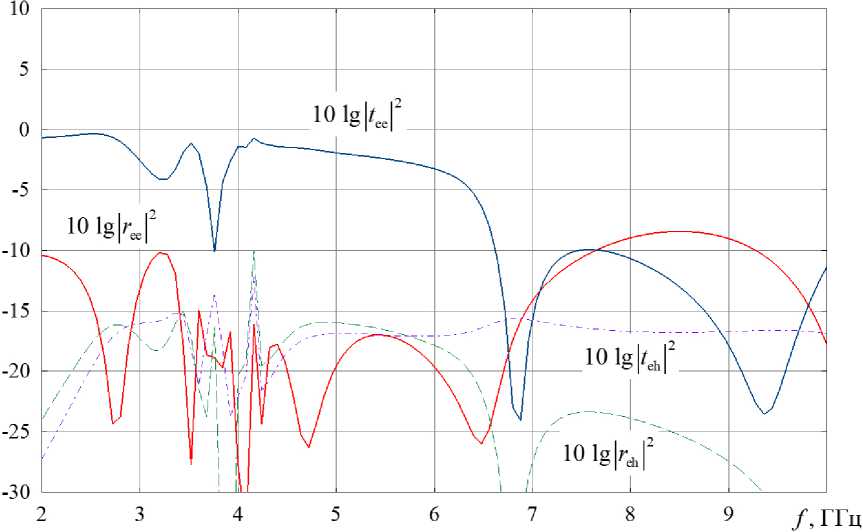
Рис. 5. Частотные зависимости прошедшей и отраженной мощностей для метаматериала на основе составных элементов из 3 спиралей

Fig. 5. Frequency dependences of the transmitted and reflected powers for a metamaterial based on constituent elements of 3 spirals

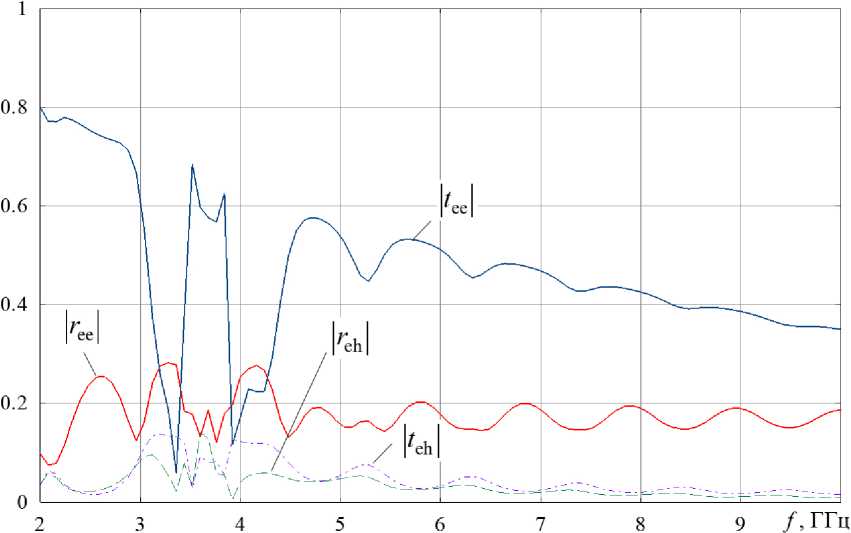
Рис. 6. Частотные зависимости модулей коэффициентов отражения и прохождения для метаматериала на основе 3-заходных гаммадионов

Fig. 6. Frequency dependences of the reflection and transmission coefficient modules for metamaterial based on 3 input gamadions

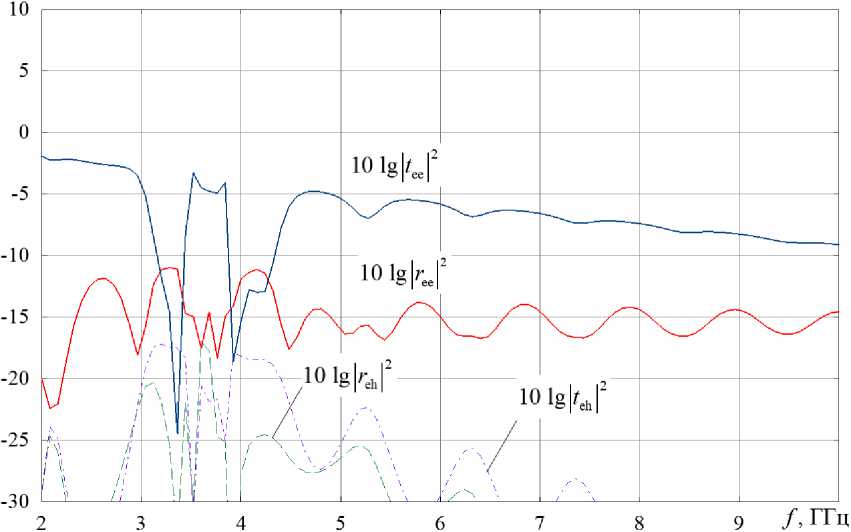
Рис. 7. Частотные зависимости прошедшей и отраженной мощностей для метаматериала на основе 3-заходных гаммадионов

Fig. 7. Frequency dependences of past and reflected powers for metamaterial based on 3 input gamadions вблизи резонансной частоты в диапазоне от 3 до 4 ГГц уровни отражения и прохождения кросс-поляризованной компоненты поля сравнимы по величине с основной компонентой. С ростом частоты уровень прохождения основной компоненты снижается, но значительно меньше, чем в случае метаматериала на основе составных спиральных элементов. Также с ростом частоты уменьшаются уровни отражения и прохождения кросс-поляризованной компоненты поля. Таким образом, для случая метаматериала на основе N-заходных гаммадионов на частотах вдали от резонанса уровень кросс-поляризации значительно меньше, чем для метаматериала на основе составных спиральных элементов. Этот факт объясняется тем, что спирали относятся к трехмерным киральным элементам, в то время как гаммадио-ны – к двумерным, в которых, как известно, степень киральности на порядок ниже. Однако интересным, на наш взгляд, является тот факт, что даже в метаматериале на основе двумерных гамма-дионов удалось получить частотно-селективный эффект преобразования нормально падающего СВЧ-излучения в азимутальное рассеяние в плоскости слоя.

Также было доказано, что метаструктура на основе N-заходных гаммадионов является искус-

ственной брэгговской решеткой в оптическом диапазоне, так как длины волн резонансных минимумов ослабления прошедшей мощности основной компоненты поля подчиняются условию Вульфа – Брэгга:

2 d ( ε ₂ µ ₂ - χ ² ₂ ) - cos² θ = νλ , (20) где ν – порядок резонанса; λ – длина волны; θ – угол падения волны.

В работе были построены математические модели метаматериалов на основе равномерно распределенной совокупности составных спиральных элементов и многозаходных гаммадионов с учетом дисперсии их материальных параметров. В результате решения задачи об отражении плоской электромагнитной волны линейной поляризации от планарных слоев из указанных метаматериалов показано, что структуры обладают ярко выраженными частотно-селективными свойствами. Обнаружены частотные режимы, в которых метаматериалы позволяют преобразовывать нормально падающее электромагнитное излучение СВЧ в азимутальное рассеяние.

Accepted 14 February 2020

Mathematical models of chiral metamaterials based on multi-turned conductive elements

M.V. Aralkin1, A.N. Dement’ev2, O.V. Osipov3

• ¹    The Military Academy of Strategic Rocket Troops after Peter the Great

  • 8, Karbysheva Street, Balashiha, Moscow Region, 143900, Russia ² MIREA – Russian Technological University

    78, Vernadsky Avenue, Moscow, 119454, Russia ³ Povolzhskiy State University of Telecommunications and Informatics

    23, L. Tolstoy Street, Samara, 443010, Russia

Аралкин Михаил Вячеславович, 1974 г. р., техник кафедры № 28 Военной академии Ракетных войск стратегического назначения имени Петра Великого. Окончил МГТУ им. Н.Э. Баумана в 1999 г., инженер-разработчик по специальности «ракетостроение».

Область научных интересов : электродинамика метаматериалов, антенны и устройства СВЧ, нелинейная оптика.

Mikhail V. Aralkin was born in 1974, Technician of the Department No. 28, the Military Academy of Strategic Rocket Troops after Peter the Great, Balashiha, Moscow Region, Russia. He graduated from Moscow State Technical University N.E. Bauman in 1999 as a development engineer specializing in rocket science.

Research interests : electrodynamics of metamaterials, antennas and microwave devices, nonlinear optics.

Andrei N. Dement’ev was born in 1975, Doctor of Sciences in Technical Sciences, Associate Professor of the Department of Radio Wave Processes and Technologies, Institute of Radio Engineering and Telecommunication Systems, MIREA – Russian Technological University, Moscow, Russia.

Research interests : electrodynamics of metamaterials, antennas and microwave devices, nonlinear optics.

Oleg V. Osipov, Doctor of Sciences in Physics and Mathematics, Vice-Rector for Science and Innovations of the Povolzhskiy State University of Telecommunications and Informatics, Samara, Russia.

Research interests : electrodynamics of metamaterials, antennas and microwave devices, nonlinear optics.

Антипов, О.И.

Детерминированный хаос и фракталы в дискретно-нелинейных системах / О.И. Антипов,

В.А. Неганов, А.А. Потапов. – М.: Радиотехника, 2009. – 235 с., ил.

ISBN 978-5-88070-237-4