Математические модели мониторинга и контроля электропотребления с учётом фактора сезонности

• 1.    Введение. В последние годы возрос интерес к моделированию электропотребления, см., например, работу Е.А. Прониной [5].

В настоящей статье предлагаются математические модели для моделирования и контроля уровня электропотребления по месяцам и по дням. Исследование в данном направлении было начато в выпускной квалификационной работе студентки РГУТИС Т.С. Сярминой [8, 9] под руководством перво- го автора настоящей статьи.

За эмпирическую основу исследования взяты реальные статистические данные за 2015 г. по электропотреблению y(m) на общедомовые нужды по месяцам m в одном конкретном московском многоквартирном доме [8, 9]. Соответствующий вариационный ряд y(m) , где m = 1, 2, 3, ..., 12, представлен в табл. 1, а также зигзагообразным графиком на рис. 1 (см. ряд 1).

Таблица 1 - Динамика потребления электроэнергии по месяцам

Месяц ( m )	1	2	3	4	5	6	7	8	9	10	11	12
Градусный номер месяца	15о	45о	75о	105о	135о	165о	195о	225о	255о	285о	315о	345о
Радианный номер месяца	π 12	3 π 12	5 π 12	7 π 12	9 π 12	11 π 12	13 π 12	15 π 12	17 π 12	19 π 12	21 π 12	23 π 12
Электропотребление y ( m ) , (кВт ⋅ ч)	1001	787	826	646	675	650	704	807	876	813	757	1075

1     2     3     4     5     6     7     8     9     10    11    12

Ряд1       Ряд2

Рис. 1 - Фактический (ряд 1) и теоретический (ряд 2) уровни электропотребления по месяцам

Цель математического моделирования – найти теоретический (расчётный) уровень электропотребления для данного вариационного ряда посредством какой-нибудь конкретной моделирующей функции E(t) непрерывного времени t, которое измеряется также дискретно: в месяцах m (1 < m < 12) или днях d(1 < d < 365). Моделирующая функция должна учитывать систематические факторы, воздействующие на фактические (наблюдаемые) уровниy(t) потребления электроэнергии, таким образом, что случайные отклонения y(t) -E(t) фактических значений y(t) от теоретических E(t) являются результатом воздействия остаточных факторов. Мы предполагаем, что при каждом фиксированном значении t случайные показания счётчика потреблённой электроэнергии y(t) в момент времени t распределены по нормальному закону с математическим ожиданием E(t) и постоянным стандартным отклонением Ϭ. Описанный стохастический процесс будет служить основой предлагаемого в работе метода мониторинга и контроля электропотребления.

2.    Модель электропотребления по месяцам

Как известно, длина светового дня зависит от широты места. В экваториальных городах, таких как, например, Кито (столица Эквадора) нет существенной разницы в длине светового дня в течение года, а в городах, доста- точно близких к экватору, эта разница составляет пару часов, например, около двух с половиной часов в Рио-де-Жанейро. В таких городах фактор сезонности практически отсутствует, и в качестве теоретического уровня электропотребления имеет смысл взять постоянный уровень. Однако для московского региона мы рассматривает фактор сезонности как основной, и моделируем теоретический уровень синусом. Мы сгладили данные ряда y(m) из табл. 1 по первой гармонике Фурье и смоделировали (теоретический) уровень электропотребления (кВт⋅ч) по месяцам m в этом доме следующей формулой:

(2 m - 1) п

E month⁽ m ) = a 0 + a l cos 12

(2 m - 1) п + b 1 sin-—^

801,4 + 128,6cos ⁽² m ₂ ^{1) k} - 52,5sin ⁽² m ₂1^{) к} ,

( 1 <  m <  12 )

где    801,4    =    среднее    значение

Emonth = 12Zm=1 У(m), а выражение под сину- сом и косинусом равно радианному номеру месяца m (см. табл. 1). Наш способ радианной нумерации месяцев даёт более адекватный результат благодаря сдвигу на ^ по сравне- нию с традиционной радианной нумерацией месяцев [10], в которой радианный номер ме- сяца m берётся равным

2 m п

Коэффициенты a 0 , a 1 , b 1 гармоники (1)

рассчитаны методом наименьших квадратов по известным формулам [10]. Полученный результат иллюстрируется рис. 1, на котором фактические и теоретические значения электропотребления для наглядности представлены на одной координатной плоскости. Видно, что теоретический уровень, даваемый первой гармоникой ряда Фурье (ряд 2, плавный график), довольно хорошо моделирует фактические уровни электропотребления по месяцам (ряд 1, зигзагообразный график). Мы берём модель (1) в качестве теоретического уровня в месячных колебаниях электропотребления в доме.

Чтобы определить, насколько та или иная математическая модель адекватна, вычисляется сумма квадратов отклонений фактических данных от теоретических значений, обозначаемая RSS (Residual Sum of Squares [2]): 12

RSS = ^ ⁽ У ^{( m} ) ^- E month ^{( m} ) ) ² .        (2)

m = 1

Чем RSS меньше, тем модель точнее и адекватней. Мы вычислили значения суммы квадратов отклонений фактических данных y(m) от среднего значения E month - 801,4 , от линейной регрессии и от первой гармоники Фурье (1). Оказалось, что линейная регрессия даёт приблизительно такую же точность, что и постоянная средняя, в то время как модель Фурье даёт значительное увеличение точности, а именно: RSS ≈ 80 017 . Таким образом, модель Фурье наиболее адекватна. Последний вывод неудивителен, так как модель Фурье учитывает фактор сезонности, влияние которого заметно даже при беглом взгляде на табл. 1.

3.    Модель электропотребления по дням

Поделив функцию (1) на 30 и соответствующим образом преобразуя аргумент, получаем модель электропотребления по дням d ( 1 < d < 365 ) в виде следующей функции:

В РОССИИ

E day ( d ) = ^( 801,4 + 128,6^ (2 ! ^ - 52,5sin (2 d ^⁾ⁿ ) -

« 26,7 + 4,3cos 2 ⁿ d - 1,8sin 2 ⁿ d - 26,7 + 4,7sin ( ^( 70 — d ) ) ,

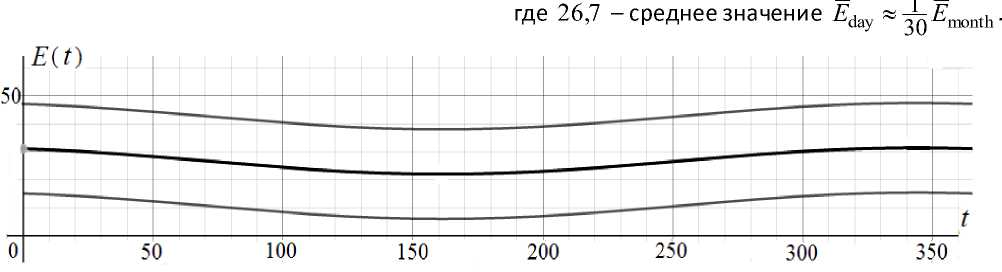
Рис. 2 – Теоретический уровень электропотребления по дням (в середине) и его трубчатая контрольная окрестность

Итак, окончательно получаем следующую синусоидальную модель теоретического уровня электропотребления по дням:

E ( t ) = 26,7 + 4,7 sin ( ^ ( 70 - t ) )

( 1 ≤ t ≤ 365 )     (3)

График функции (3) изображён на рис. 2 (средняя кривая).

Электропотребление за каждый месяц m (1 ≤ m ≤ 12) складывается из количеств суточных электроэнергий, потреблённых в этом месяце: Emonth(m) = ZEday(d), где d пробе-d гает значения от номера первого (порядкового в году) до номера последнего дня месяца m.

Например, E month (11) = Z E day ( d ) .

d = 305

Однако в расчётах часто бывает удобно перейти от дискретного времени d к непрерывному времени t . Тогда, используя нашу модель (3), легко вычислить количество электроэнергии E time period , теоретически расходуемое за любой определённый период времени, например, с 7 октября по 26 ноября. Замечая, что эти даты соответствуют 280-му и 330му дням года соответственно, и, учитывая, что аргументы тригонометрических функций измеряются в радианах, находим E time period с помощью калькулятора:

Etime period   Z E (d ) ” P d=280       280

J [ 26,7 + 4,7sin ( 32^ ( 70 — t ) ) ] dt =

= ( 26,7 1 + ³65 4,7cos ( .2П (70 — t ) ) ] ³³0 2 n         ^x365            280

« 8 747 - 7 233 = 1514 кВт - ч.

Как уже было отмечено во введении, наша модель основана на стохастическом процессе, у которого в каждый фиксированный момент времени t, измеряемого в днях года (1 ≤ t ≤ 365), имеется свой теоретический уровень электропотребления E(t), а фактические случайные показания счётчика потреблённой электроэнергии в этот момент времени t распределены по нормальному закону с математическим ожиданием E(t) и постоянным стандартным отклонением.

В качестве несмещённой оценки для дисперсии случайных фактических измерений месячных показаний счётчика вокруг теоретического уровня (1), мы берём величину 52   -  1 RSS « ',80 017»7 274, исполь- mont    12-1        11

зуя значение RSS ≈ 80 017, полученное в кон- це раздела 2. Отсюда находим, что месячное стандартное отклонение от теоретического уровня (1) равно smonth ≈ 85. Суточное стандартное отклонение sday от теоретического уровня (3) приблизительно в 30 раз меньше, потому что фактические (случайные) показания счётчика потреблённой электроэнергии за дни d1 и d2 независимы при любых d1 и d2 (1 ≤ d1, d2 ≤ 365), и, значит, дисперсия sm2 onth суммы тридцати независимых случайных показаний счётчика (за целый месяц) равна сумме тридцати соответствующих дисперсий 52 . Таким образом, s * smonth * 85 * 16.

day , day 30 30

На рис. 2 изображена трубчатая контрольная окрестность теоретического уровня E(t) с постоянным радиусом s day = 16.

Адекватность нашей модели определяется тем, насколько адекватно определены теоретический уровень и стандартное отклонение. Модель наиболее проста в экваториальных городах, таких как Кито, где теоретический уровень есть константа, а трубчатая контрольная окрестность – прямоугольник.

4.    Мониторинг и контроль

Мы предлагаем следующий метод мониторинга и контроля электропотребления. В каждый конкретный день d ( 1 ≤ d ≤ 365 ) фактическое суточное потребление электроэнергии есть нормальная случайная величина с математическим ожиданием E day (d) и постоянным стандартным отклонением s day . В конкретном примере, рассматриваемом в этой работе, s day (d)= 16 (см. раздел 3). Хорошо известное из статистики «эмпирическое правило» («Empirical Rule» [4]) гласит, что в каждый конкретный день d вероятность попадания нормальной случайной величины в интервал

E day ( d ) — S _day, E day ( d ) + S day ) (5) приближённо равна 0,68. Таким образом, в среднем 117 дней в году фактический уровень электропотребления выходит за пределы трубчатой контрольной окрестности радиуса s day вокруг теоретического уровня E day (d) , показанной на рис. 2.

Предположим, что показания потреблённой электроэнергии мониторятся на ежедневной основе. Рассмотрим последовательность 365-ти независимых испытаний Бернулли, в которой для каждого d -го испытания успехом считается попадание в интервал (5) количества электроэнергии, фактически потреблённой за конкретный день d . Предположим, что в какой-то день d значение вышло из интервала (5), т.е. за пределы трубчатой контрольной окрестности на рис. 2. При этом условии вероятность того, что в следующие (конкретные) три дня подряд (т.е. с порядковыми номерами d+1, d+2 и d+3 ), уровень фактического потребления окажется за пределами трубчатой контрольной окрестности, равна (1 – 0,68)³≈0,03 .

Таким образом, когда при ежедневном мониторинге измеренные значения потреблённой электроэнергии держатся за пределами трубчатой контрольной окрестности четыре или более дней подряд, имеются основания уведомить пользователя о том, что у него наметились предпосылки для одной из следующих двух тенденций:

• а)    тенденции к перерасходу электроэнергии (когда измеренные значения оказываются выше верхней границы трубчатой контрольной окрестности на рисунке 2) или же, наоборот,

• б)    тенденции к недорасходу электроэнергии (когда ниже нижней границы контрольной окрестности).

5.    Заключение: «умный энергометр»

После получения такого уведомления управляющей компании имеет смысл провести расследование или простой энергоаудит. В случае (а) причиной могут быть, например, несанкционированные подключения к электросети, а в случае (б) причиной могут быть, например, недавно проведённые энергосберегающие мероприятия. В случае (а) следует принять оперативные меры, чтобы вернуть процесс внутрь трубчатой окрестности вокруг теоретического уровня, а также оценить ущерб, сравнивая фактически потраченную электроэнергию с соответствующим теоретическим значением E time period , как в (4). В случае

В РОССИИ

(б), сравнивая с E time period , можно оценить уже положительный эффект от проведённых энергосберегающих мероприятий и затем пересчитать и обновить сам теоретический уровень (3).

Следуя известному методу [7], мы вывели следующую формулу, моделирующую длину светового дня в Москве (в часах):

L (t) = 12 + 5,285sin(2^ (t - 80)) (6) (1 ≤ t ≤ 365), где время t измеряется в днях года, как и в формуле (3). Похожесть выражений под синусом в (6) и (3) ещё раз подтверждает адекватность сезонной модели (3), а противоположность их знаков обусловлена тем, что графики этих синусов (без учёта коэффициентов вне них) зеркально симметричны относительно оси d (лишь с небольшим сдвигом на 10 дней). Такая перевернутость ожидаема. Она вызвана тем, что, например, дню летнего солнцестояния соответствует (теоретически) минимальный уровень электропотребления, а дню зимнего – максимальный.

В заключение этого раздела отметим как недостаток нашего метода то, что, используя эмпирическое правило, мы вместо истинных значений Ϭ(d) стандартных отклонений использовали их усреднённую оценку sday. Есть разные способы справиться с этой трудностью [6, С. 401]. Одним из способов улучшения точности было бы наличие ежедневных фактических данных по электропотреблению за год, а ещё надёжнее исходить из их усреднённых данных на ежедневной основе за период в несколько лет. У нас же были лишь 12 данных электропотребления по месяцам одного года. Для стандартных отклонений имеет смысл искать свой теоретический уровень, подобно тому, как мы нашли теоретический уровень для значений потребляемой электроэнергии. Эти задачи авторы планируют подробнее рассмотреть в будущих публикациях.

Мы предлагаем принцип работы прибора, который называем «умным энергометром», для мониторинга электропотребления, позволяющий вовремя обнаружить перерасход (или недорасход) электроэнергии, чтобы принять оперативные превентивные меры. При мониторинге на ежедневной основе прибор сигнализирует пользователю о нештатном повышении (или понижении) уровня электропотребления при выходе за пределы трубчатой контрольной окрестности четыре дня подряд (раздел 4). Мы выражаем надежду на то, что наш прибор – «умный энергометр» – будет полезным дополнением к так называемым системам мониторинга и планирования энергопотребления («Monitoring and Targeting» [1]).

В заключение сформулируем важный тезис, который сегодня, к сожалению, многие почему-то не одобряют и даже не понимают. Этот тезис состоит в том, что статистически грамотный мониторинг электропотребления – это ключ к воплощению энергосберегающих мер. Наш тезис согласуется с популярным сегодня подходом управления, основанном на цикле DMAIC, второе и пятое звенья которого соответственно означают Measure и Control [3].