Математические модели обратных задач динамики дефектных конструкций

Одним из наиболее простых вариантов задачи обратной динамики является определение жесткости многоэтажного здания по фактическим величинам собственных колебаний, замеренных при помощи высокоточных приборов. Среди различных задач обратной динамики [1-3] определение жесткостных свойств здания является, безусловно, устойчивым в вычислительном плане и не относится к категории некорректных задач [3-5]. Однако для нахождения параметров жесткости по результатам определения частоты основного тона приходится пользоваться некоторым приближением расчетной схемы, вносящим погрешности в определение собственных параметров здания [4; 6]. Можно отметить, что определение величины потери жесткости характеризует количественную оценку накопления дефектов здания, подверженного некоторому периоду эксплуатации [4], что оказывает влияние на функциональные свойства несущих конструкций [7]. Методы такой оценки на основе динамических испытаний имеют явные преимущества, поскольку исключают необходимость демонтажа ограждающих конструкций для обследования внутренних несущих конструкций здания1. Необходимо заметить, что обязательные периодические определения частот собственных колебаний основного тона здания определены для сейсмических регионов условиями государственных стандартов1.

1 Постановка задачи

Решение обратной задачи динамики является не единственной причиной, обусловливающей потребность в оценке точности определения собственных динамических параметров; стоит привести примеры необходимости такой оценки при выборе дискретной расчетной схемы и определения уровня дискретизации, который в большинстве случаев бывает излишне высоким [6; 8; 9].

Подавляющее преобладание завышения размерности задач динамики в расчетной практике не исключает возможность формирования динамических моделей «малой» размерности, не отражающих с достаточной точностью необходимые динамические свойства рассчитываемого объекта [10].

Среди прочих задач оценки погрешности определения собственных динамических параметров многоэтажных зданий актуальна задача определения погрешности при использовании простейших расчетных схем с сосредоточенными массами [6; 10]. Распространенные способы определения решений подобных задач основаны преимущественно на применении преобразований подобия [11; 12].

Использование подобных оценок не учитывает специфику конструктивных элементов рассчитываемого сооружения, и решение такой задачи является, на наш взгляд, чрезвычайно актуальным.

Рассмотрим величины погрешностей, получаемых при аппроксимации различных конструктивных элементов одномассовыми динамическими моделями.

Консольная система с подавляющим преобладанием деформаций сдвига и равномерным распределением масс. Такими конструктивными элементами являются диафрагмы жесткости и несущие стеновые конструкции зданий [6].

С использованием метода динамических перемещений [13] расчетная схема такого конструктивного элемента может быть представлена в виде вертикального стержня с распределенной массой интенсивности р , длины l и сдвиговой жесткости GF , где G — модуль сдвига, F — площадь поперечного сечения (рис. 1).

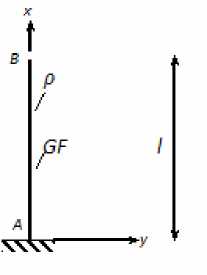
Рис. 1. Расчетная схема элемента с деформациями сдвига, с распределенной массой ρ

Уравнение собственных колебаний такого элемента является уравнением в частных производных и имеет вид:

+ ^ 2 ^ • GF = 0,                (1)

d t ²     d x ²

где v — горизонтальные перемещения точек элемента в процессе собственных колебаний, t — параметр времени. Допустим, что собственные колебания такой системы осуществляются с некоторой частотой w.

Тогда с использованием приема разделения переменных [14] можем записать v (t, x) = y (x) • sin (tot).                              (2)

При подстановке (2) в (1) имеем обыкновенное дифференциальное уравнение:

- р • to2 • y(x) • sin(tox) + GFy"(x) • sin(tox) = 0, после упрощения которого получаем следующее уравнение:

У"(x)- p-- ■ У (x ) = 0. GF

Характеристическое уравнение для (3) имеет вид:

p2 - po = 0.

GF

Корни этого уравнения имеют вид:

p 1 = o.

p2 = -o.

или p1 = op. , p2 = -юр , где p =

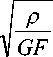
Общее решение уравнения (3) представляет собой линейную комбинацию двух линейно независимых частных решений, образующих базисную вектор-функцию:

h(x) = [sin(op x), cos (opx)].

В этом случае решение имеет вид:

У(x ) = Ci ■ sin(opx)+ C2 ■ cos(opx), где C1 , C2 — коэффициенты линейной комбинации, определяющиеся краевыми условиями уравнения (3) [15].

При x = 0 имеем равенство:

C ₂ ■ cos ( op x ) = 0 , откуда C 2 = 0 .

Таким образом, с учетом закрепления узла в точке x = 0 имеем реше ние:

У(x )= Ci ■ sin (opx).

Поскольку функция колебательной формы при собственных колебаниях определена с точностью до множителя, то C ₁ положим равной 1, тогда

y (x ) = sin (opx).

При перемещении точки B на некоторую величину А имеем равенство:

sin ( op l ) = А .

В частности, при А = 1 получаем равенство вида:

Г

C 1 ■ sin

(opl )=siJ ^Gf

v

^

■ l

= 1.

Если на точку B , перемещенную на величину А = 1, наложить горизонтальную связь (рис. 2), то в этой связи возникает реакция H_B , равная

Eb ^ yx

d x

= cos(юц1 )• EI • юц .

x =1

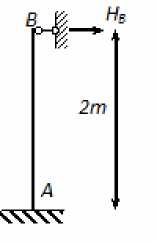
Рис. 2. Расчетная схема для определения реакции H_B в линейной связи верхнего узла элемента АВ

При воздействии единичной силы по направлению связи амплитуда гармонического перемещения у ( l ) определяется выражением:

У (l ) =

cos( юц1 )• EI • юц

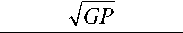
cos( юц1 )• EI • ЮР

cos(a^l )• Ю Ер

. (4)

При величине резонанса амплитуда достигается при знаменателе выражения (4), равном нулю. При этом

cos(aцl ) = 0.

Низшая частота собственных колебаний определяется в этом случае из равенства:

УЦ1 = 2-

Таким образом, частота ух колебаний низшего тона такой системы определяется выражением:

п

Y 1 =ТТ

2 ц 1

к GF 21 У Р

Воспользовавшись этим выражением, оценим относительную величину остаточной жесткости здания, полученную в результате инструментальных замеров, определивших частоту /1 r собственных колебаний основного тона. Если /1р — исходная (проектная) частота собственных колебаний здания, то отношение q остаточной жесткости к изначальной определяется в виде:

q =

(

Ухт

k Y1p 7

Определим относительную величину остаточной жесткости здания в аппроксимации модели конструкций с массами, сосредоточенными в уровнях перекрытий.

Рассмотрим приближение наиболее простой динамической системы, представленной двухэтажным зданием. Частоты собственных колебаний такой системы могут быть определены достаточно просто. Расчетная схема двухэтажной конструкции с массами, сосредоточенными в уровне перекрытий, изображена на рис. 3.

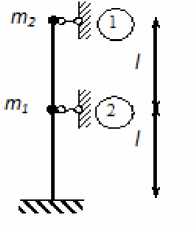
Рис. 3. Динамическая модель двухэтажного здания со стеновыми несущими конструкциями. 1, 2 — номера связей

Для построения системы уравнений динамического равновесия используем метод перемещений [6], для чего на перемещения точек сосредоточения масс наложим линейные связи в горизонтальном направлении (рис. 3).

Сосредотачивая массы здания в точках, обозначим величины масс через m ₁ и m ₂ .

Матрица R единичных реакций такой системы имеет вид:

Г 2 GF   GF "

R = l l

R _ GF   GF "

_ l          l .

Матрица D динамических реакций модели имеет вид:

" 2GF     GF" l- m1        l- m1 D     GF    GF "                   (5) _ _ l - m 2 l - m 2 При m1 = m 2 = m частоты собственных колебаний могут быть определены из условия

| D -X-E\ = 0,                              (6)

где X — собственные значения, E — единичная матрица.

В развернутом виде уравнение (6) может быть записано следующим образом:

2GF _Y GF a (GF Y „ --Л II--Л l-l ----- I = 0 . l • m a l • m J Г l' m J

Корни уравнения (7) определяются в виде:

Л = 3GF(Il • m)m

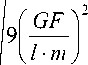
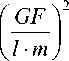
Л 2 = GF ( з m 2V2 ) . l • m

Таким образом, минимальное собственное значение:

Л= GF (3 - 2V2), l • m а минимальная частота собственных колебаний /1 определена в виде:

Y 1 = 41 = = / GF ( з - 2V2 I . V l • m

В этом случае отношение q остаточной жесткости к изначальной, как и для модели с распределенными параметрами масс, определяется в виде:

q =

( hr

( Y1P J

Компоненты вектора A ₁ собственных колебаний определим из решения системы уравнений:

( D - Л ^ E ) A = 0, где A = ( a 1 a 2 ) T — собственный вектор двухмерной динамической системы, соответствующий собственному значению у 1 .

Если в выражении (5), определяющем матрицу D , жесткость GF вынести множителем, то оставшиеся коэффициенты матрицы определяются только через геометрические и инерционные параметры здания. Считая эти параметры неизменными в процессе эксплуатации здания, для выражения величины q получаем неизменным равенство (9).

Выполняя аналогичные преобразования для здания большей этажности при условии сохранения геометрических и инерционных параметров здания, приходим к неизменности выражения относительной величины остаточной жесткости в виде (9).

Заключение

• 1.    Условие сохранения геометрических и инерционных параметров конструкций в процессе эксплуатации является достаточным для определения относительной величины остаточной жесткости в виде (9) при наличии конструктивных элементов с распределенными и сосредоточенными параметрами масс.

• 2.    Величина инвариантна по отношению к проявлениям свойств дискретности и непрерывности инерционных параметров конструктивных элементов.